2. 北京师范大学天文系, 北京 100875;
3. 中国科学院太阳活动重点实验室, 北京 100012
2. Department of Astronomy, Beijing Normal University, Beijing 100875, China;
3. Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China
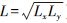 ) virtually observes the power-law and self-similarity. (2) The value and signal-to-noise ratio of BP's production decrease with the increase of BP's scale. Numerous small-scale BPs could be a valid source of energy for the heating of upper atmosphere. For instance, BPs with a scale smaller than 4″ share approximately 53.23% of the sample's total light flux budget. (3) As the active region decays, the numerical density of small-scale BPs also decreases. (4) The distribution of the sample set's scale observes the power-law, with a dispersion index σ(ζ) of 4%. The power-law index γ of the observed and low-noise (L≤8″) samples are respectively 1.97 and 2.12. (5) However, within the observation time, the overall power-law index γ does not converge. The relationship between the power-law index and the time-span of observation is serrated: in quiet times γ gradually increases, while in active moments γ decreases sharply. (6) The instantaneous γ is reversely proportional to the instantaneous total light flux. Even after filtering large-scale BPs (L > 8″), the low-noise sample, which contains only middle-and small-scale BPs, still shows such correlation. This quashes our initial suspicion that the numerical calculation of γ is rigged by the injection of few large BPs into the sample pool; the observed relationship between large events and the dropping of γ is intrinsic. Solar activities not only produces middle and large scale BPs, but also changes the entire pattern of BP's distribution and hence lowers γ.
) virtually observes the power-law and self-similarity. (2) The value and signal-to-noise ratio of BP's production decrease with the increase of BP's scale. Numerous small-scale BPs could be a valid source of energy for the heating of upper atmosphere. For instance, BPs with a scale smaller than 4″ share approximately 53.23% of the sample's total light flux budget. (3) As the active region decays, the numerical density of small-scale BPs also decreases. (4) The distribution of the sample set's scale observes the power-law, with a dispersion index σ(ζ) of 4%. The power-law index γ of the observed and low-noise (L≤8″) samples are respectively 1.97 and 2.12. (5) However, within the observation time, the overall power-law index γ does not converge. The relationship between the power-law index and the time-span of observation is serrated: in quiet times γ gradually increases, while in active moments γ decreases sharply. (6) The instantaneous γ is reversely proportional to the instantaneous total light flux. Even after filtering large-scale BPs (L > 8″), the low-noise sample, which contains only middle-and small-scale BPs, still shows such correlation. This quashes our initial suspicion that the numerical calculation of γ is rigged by the injection of few large BPs into the sample pool; the observed relationship between large events and the dropping of γ is intrinsic. Solar activities not only produces middle and large scale BPs, but also changes the entire pattern of BP's distribution and hence lowers γ.
太阳活动的一个典型统计特征是耀斑能量的幂律分布。在硬X射线[1-4]、软X射线[5-8]和极紫外[9-10]波段, 耀斑和微耀斑的峰值辐射通量、爆发频率、尺度和寿命基本呈幂律分布[11]。幂律分布的基本表达形式:
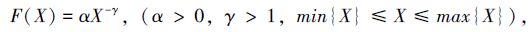
|
(1) |
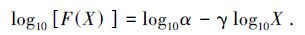
|
(2) |
其中, X为表征耀斑能量的某受测量;F (X)为其频数密度。例如, 硬X射线耀斑的光子流量I(E) 与光子能量E的关系符合幂律分布[5]:
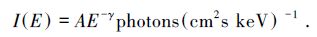
|
(3) |
太阳活动基本满足幂律分布的自相似性,即对于两个容量不同、但γ相近的耀斑样本, 其分布曲线的形状相似。虽然不同活动区的爆发机制、频率和强度有很大差异,但是,个体活动区上亮点的幂律分布和在全日面、长时标数据上对大量太阳活动的统计中得到的幂律分布在图形和机理上基本相似[12-13],二者都是太阳活动内禀的性质。作为一个无标度的复杂网络,太阳活动总体的幂律分布是大量无标度分布的综合。在无标度复杂网络中,规模迥异但演化机制相同的复杂网络结构常表现出自相似性 (分形)。不同规模的能量连锁耗散事件发生的几率与其规模不相关,会形成形状相似、幅度不同的幂律分布。这种现象在实验、空间和模拟的等离子体中普遍存在[14]。因此,各种尺度的活动区产生的活动也在一定程度上具有自相似性。
亮点的幂律分布可能具有与太阳活动的周期性相对独立的性质。虽然在全日面、跨越太阳周的统计中, 日冕亮点的分布具有时空的周期性。在空间上,爆发事件频发的区域与强磁场的分布带[15]基本吻合[16]。在时间上,太阳活动的剧烈程度变化有11年的长周期和若干个短周期[3, 17],还有一定的随机性[18],这种周期性还造成了地球电离层的周期变化[19]。但是,多项研究表明[3, 5, 11, 20],耀斑的频数分布不仅基本维持幂律分布,而且其幂指数γ并没有表现出与太阳周明确的相关性,γ的涨落小于线性回归的不确定性。例如,在文[7]对24年间 (1976~2000) 地球静止轨道环境业务卫星 (Geostationary Operational Environmental Satellites, GOES) 观测的5万余个耀斑的统计研究中,太阳周峰年和谷年的软X射线峰值流量分布有很接近的幂指数。这可能意味着,耀斑的幂律分布是一个与太阳活动的剧烈程度相对独立的统计规律,其背后的物理机制并不随太阳周变化。但是,也有统计表明,γ具有周期性,例如,文[4]认为,γ随太阳周变化, 在峰年较大,谷年较小。
在使用多个波段对太阳活动的统计结果中,实测频数分布的中段往往与幂律吻合较好;而在能量较低的一端,实测频数往往低于幂律。这种偏差在相当程度上由观测设备的局限性造成。一方面,实测频数受观测设备在背景噪声中识别低能量事件的阈值的限制,降低观测设备的阈值能够大幅度提高所获取的小规模样本的容量。例如,文[1]使用搭载于轨道太阳观测台7号卫星 (Orbiting Solar Observatory 7, OSO-7) 的由加州大学圣地亚哥分校 (University of California, San Diego, UCSD) 研制的硬X射线探测器对X射线爆发进行统计,该设备的低端阈值约为0.3(cm2s keV)-1。在统计结果中,20 keV的峰值流量Am在1~10(cm2s keV)-1的区间是光滑并且符合幂律的;但在Am<0.5(cm2s keV)-1段,频数明显低于幂律并形成平台。而文[2]使用了低端阈值比UCSD小一个数量级的X射线探测器,所观测的X射线爆发20 keV峰值流量的频数分布在0.01~0.1(cm2s keV)-1段都是光滑并且符合幂律的。另一方面,对小规模个体的实测频数受观测设备时间和空间分辨率的制约。数量巨大的短时标个体由于其寿命近似或低于时间序列的间隔而被漏检,而尺度小于设备衍射极限的邻近个体又可能被合并,因而无法准确统计其频数。例如,文[21]使用大熊湖的新太阳望远镜 (New Solar Telescope, NST) 和太阳光学望远镜对光球磁亮点的比较观测研究中,新太阳望远镜 (衍射极限为77 km) 不但可以将太阳光学望远镜 (衍射极限为157 km) 所观测到的亮点个体分解为多个更小尺度的亮点。而且,在新太阳望远镜 (时间分辨率达6 s-1) 的观测样本中,98.6%的光球亮点的寿命短于太阳光学望远镜的观测间隔时间 (120 s),所以不一定能被太阳光学望远镜检测到。对小规模个体有较高漏检率的情况也出现在对低色球层亮点[22]和行星际磁通量绳[23]的观测统计中。
幂律分布不可能向零无限延伸,极小规模的亮点必然有独特的分布规律。如果完全按照幂律分布αE-γ,则日面上亮点产生的总能量:
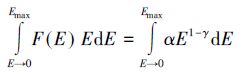
|
(4) |
将趋近于无穷[24],而实际的太阳亮点产生的总能量一定是收敛的,这也是分布函数归一性的要求。这就意味着,亮点完全样本的频数分布曲线必然在低端存在一个拐点,小于该拐点规模的频数低于幂律分布。如果该拐点是尖锐而不是圆滑的,小于该规模的亮点的数目极少,则在统计上可以认为它就是亮点的最小规模。在观测设备的发展过程中,当分辨阈值处于亮点频数分布曲线的幂律段以内时,所获得的样本容量
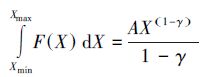
|
(5) |
会随着阈值的减小而大幅度增加。但是当阈值小于幂律低端拐点时,所能分辨的亮点数密度和相应的亮点辐射总能量会缓慢地向完全样本逼近。
幂律分布表明,太阳大气是一个能量不断输入并耗散的系统。一切太阳活动的根源是在太阳内部生成的磁场[25]。大的磁流管从对流区上浮[26],把磁能和复杂性带到了光球以上的大气中。大气磁场组成的网络是一个复杂网络[27]。它不仅有规模大、结构复杂、层次多、节点多样化等特点,还具有明显的时空复杂性。一方面,该网络不是封闭的,和大多数真实的网络一样,它具有增长性,不断有新的节点加入。自下而上不断有新的磁能和扰动的输入[28],产生新的磁场凝聚和爆发,而能量耗尽的节点又逐渐退出。太阳活动的过程,就是网络节点不断新陈代谢、拓扑和动力学性质不断演化的过程。能量从高数量级向低级跃迁[29]而发生耀斑。大的爆发能释放足够多的磁能,暂时清空可供释放的自由能,使得活动区需要一定的时间积蓄能量。这样,耀斑的能量、频率和等待时间的分布都有可能服从幂律分布。另一方面,从复杂网络节点的连接性的角度看,该网络的演化具有择优性,光球上新浮现的磁场 (及其所带来的能量和复杂性) 倾向于在原有活动区附近出现和聚集[30-31]。复杂网络中的一个新的节点并不是随机与其他k个节点发生联系,它有首先与度值较高的节点相连的倾向。这就造成高度值的节点快速增加度值、节点之间度值的差异被放大的结果,逐渐演化成了标度不变的状态,各节点的度值k就形成了幂律分布。
太阳活动的幂律分布对研究太阳高层大气的加热机制有重要意义。在色球及以上的太阳大气中,由于磁敏线的稀少,无法直接观测能量释放过程中的磁场空间结构和演化过程,而对亮点的分布特征和时变规律的准确统计为研究大气加热提供了宝贵的信息。文[32]认为,如果γ超过2,海量微小规模耀斑能够有效地加热日冕; 反之,如果γ小于2,则大耀斑的分布基本决定了总的能量输出。微观上,低层亮点的震荡有可能向上传播磁流体动力学 (Magnetohydrodynamics, MHD) 波和阿尔文 (Alfvén) 波并发生湍流耗散, 进而造成色球和日冕的加热[33-34]。
对于单个太阳活动区而言,由于其能量的有限性,所产生的爆发是否一定遵循幂律分布还不是一个很明确的问题[24, 32]。这就需要分析活动区的不同演化阶段爆发活动的分布特征与能量平衡的关系。幂指数的演变机制,尤其是幂指数与熵的关系,以及与外界驱动的关系,对于研究网络如何演化成自组织是重要线索,但目前还没研究得很清楚[35]。值得一提的是,在宁静太阳的范畴中,幂律分布不一定成立。例如,光球亮点的尺度[21, 36]和面积[37]均服从对数正态分布。
在前期工作[22]中,使用三维区域标记法对一个太阳活动区的低色球层亮点进行了识别和统计分析。主要结果是:(1) 活动区低色球层亮点的尺度、面积和光通量基本服从幂律分布;(2) 亮点寿命的频数在中等时标呈幂律分布,在长时标呈指数分布。大规模亮点的等待时间符合指数分布。亮点的产生符合泊松过程的基本特点;(3) 海量的小规模亮点有可能向日冕稳定地提供能量;(4) 微小规模亮点的实测频数低于幂律分布,这在相当程度上受观测数据的低时间分辨率所造成的低采样率的影响。
前人对于光球磁亮点的精细结构和日冕亮点的统计规律已经积累了相当丰富的观测和理论分析,对色球亮点的震荡[38]也进行了精细的观测,但是,对色球亮点的频数分布规律却只有较为稀少的研究[39]。本文使用低色球层的观测资料,侧重于分析亮点的瞬时分布在时域中的变化和累积,主要研究以下几个问题:(1) 在短时标和瞬时观测中,亮点的频数分布遵循什么规律?是否满足无标度性?(2) 亮点的瞬时频数分布特征如何随活动区整体的演化而变化?在长时标中,瞬时分布如何累积成为幂律分布?(3) 亮点瞬时分布的各参数之间有怎样的相关性?
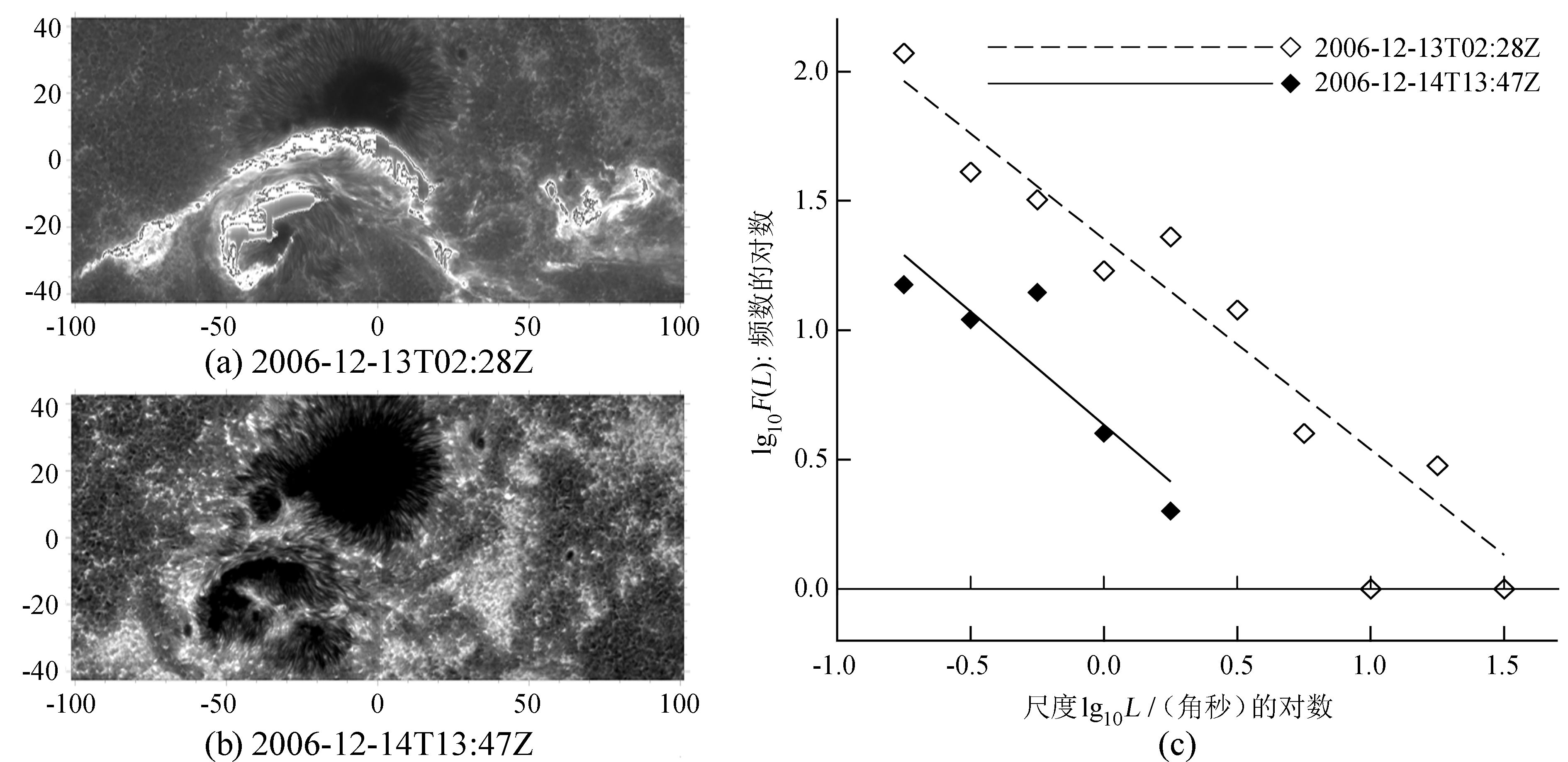
1 资料和分析方法 1.1 活动区选取一个爆发现象丰富、演化过程复杂的活动区作为研究样本。NOAA 10930活动区位于南半球赤道附近 (S05),尺度约为90″ × 100″,其主黑子是一个半径约为29″、处于稳定衰减阶段的负极性黑子。该活动区于2006年12月05日在日面东边初现时是一个β型活动区,随后,在主黑子的西侧边缘出现了多个磁浮现区,产生了二十余枚小黑子和微黑子。整体的磁场位型也相应地由β变成了β-γ-σ。图 1(a)和(b)显示了活动区的形态。在日面期间 (05~18日),AR 10930发生了7个X级和数十个C级和M级爆发。表 1列出了它的爆发事件。
|
| 图 1 NOAA 10930活动区在 (a) 活动和 (b) 平静时的Ca Ⅱ H单色像. (c) 空心和实心方框分别表示 (a) 和 (b) 中亮点尺度的瞬时频数分布 Figure 1 Ca Ⅱ H monograms of NOAA AR 10930 in (a) an active and (b) a quiet moment. The unit for coordinates is arcsecond. (c) Instantaneous distributions of BPs′ scale L plotted in double-logarithm coordinates. Hollow and solid spades respectively mark samples in panels (a) and (b) |
| 日b
day | 纬/经度 lon°/lat° | 类型 Hale | 爆发Class | |||
| C | M | X | ||||
| 05 | - | β | - | - | - | |
| 06 | S06E58 | β | 21 | 4 | 2 | |
| 07 | S05E46 | β-γ-σ | 17 | 4 | 1 | |
| 08 | S06E31 | β-γ-σ | 4 | 1 | 0 | |
| BFI | 09 | S05E18 | β-γ | 0 | 0 | 0 |
| 观测时段 | 10 | S04E05 | β | 0 | 0 | 0 |
| Observation | 11 | S05W08 | β-γ-σ | 3 | 0 | 0 |
| Time | 12 | S05W21 | β-γ-σ | 3 | 0 | 0 |
| 13 | S06W35 | β-γ-σ | 2 | 0 | 1 | |
| 14 | S05W47 | β-γ-σ | 4 | 0 | 2 | |
| 15 | S05W61 | β-γ-σ | 2 | 0 | 1 | |
| 16 | S06W73 | β-γ-σ | 0 | 0 | 0 | |
| 17 | S06W86 | β-γ-σ | 1 | 0 | 0 | |
| 18 | S06W91 | β-γ-σ | 1 | 0 | 0 | |
| (a) 摘自由“活动区监测”发布的“活动区观测摘要”; | ||||||
| (b) 2006年12月 | ||||||
| (a) Published by the NOAA/USAF Active Region Summary and retrieved from the Active Region Monitor (ARM); | ||||||
| (b) 2006 December | ||||||
使用由宽带滤光器成像仪 (Broadband Filter Imager, BFI) 获得的Ca Ⅱ H λ3 968.5波段低色球层单色像时间序列。宽带滤光器成像仪是搭载在“日出”卫星上的太阳光学望远镜的成像系统之一。宽带滤光器成像仪使用时间分辨率为1帧/120秒、像元大小为0″.106 × 0″.106、视场为217″.1 × 108″.5的参数对NOAA 10930活动区进行了124小时 (09日20: 02~14日23: 54) 的观测。该Ca Ⅱ H数据中,增亮尺度的跨度达2.5个数量级,包含耀斑、微耀斑和非爆发性的增亮,增亮区域的形状可呈椭圆、弧形或不规则形状,由于研究目的是从统计角度对低色球层增亮进行分析,所以本文中把这些尺度、形状和性质迥异的增亮区域统称为亮点。
日出卫星另有两套成像系统:极紫外成像摄谱仪 (Extreme-ultraviolet Imaging Spectrometer, EIS) 和X射线望远镜 (X-Ray Telescope, XRT)。在它们采集的图像中也有大量的亮点,蕴含丰富的物理信息。但是,与Ca Ⅱ H波段相比,一方面,它们的工作波段高度较高,没有相应高度的实测磁场数据;另一方面,极紫外成像摄谱仪和X射线望远镜的像元分辨率 (~2″) 比宽带滤光器成像仪低一个数量级,图像提供的细节信息较少,在Ca Ⅱ H像中由数十个亮点组成的团簇,在高层大气中仅表现为一个或多个亮点[40]。因此,研究选择在Ca Ⅱ H单色像上进行亮点的识别和统计,而没有使用极紫外成像摄谱仪和X射线望远镜的数据。
1.3 计算方法开发了一套基于二维区域标记的数据压缩方法,在时间序列中对亮点进行识别和统计。基本步骤如下。
(1) 图像预处理。首先,剔除原始数据中成像受干扰的坏图,矫正不准确的像素。然后对图像做投影改正,使用快速傅里叶变换相关跟踪的算法对单色像对齐,并选取观测较为连续的时间段。预处理之后的时间序列包含2 597帧图像,视场为202″.4 × 85″.3。
(2) 识别亮点。首先,使用根据亮度分布制定的阈值,把二维时间序列中的每个亮点对应的高亮度像素团簇加以标记。由于宽带滤光器成像仪的衍射极限为0″.2,使用侵蚀和膨胀的方法过滤像元 (0″.106 × 0″.106) 级的微小亮点,并对亮点区域进行孤立和抛光。然后,测量每个亮点的尺度L、面积A和光通量φ,并建立数据库。这些受测量表征了亮点的能量,在本文中泛称为规模。其中,考虑到亮点形状的不规则性,研究中对尺度的定义为亮点所占最小矩形面积的平方根 (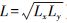
(3) 统计分析。一方面,分析瞬时亮点子集的频数分布特征量在时域中的变化;另一方面,把亮点样本集作为一个整体分析其频数分布。对于每组受测量X,首先使用对数分组以获得样本受测量的频数分布F(X)。由于频数分布及其特征量对分组的方案有相当的敏感性,采用不合理的组限会引入随机性并造成幂律分布特征值之间虚假的相关性,在经验公式[41]
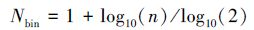
|
(6) |
的基础上对样本集和瞬时子集分别确定一个通用的组数Nbin,用于对受测量的对数log10(X) 进行等距分组。然后,使用下式[42]
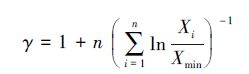
|
(7) |
估算指数γ,并对频数F(X) 使用最小二乘法进行线性回归 (2式) 以获得系数α。为了描述实测频数偏离幂律分布的相对程度,还分别在普通和对数笛卡尔坐标中计算两个离散系数:
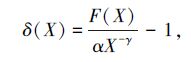
|
(8) |
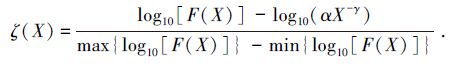
|
(9) |
对于一个频数分布,使用δ(X) 和ζ(X) 的标准差表征该分布在何种程度上符合幂律分布,称为该分布的离散系数。对于某个已经基本判定为幂律的频数分布,其中某点的δ(X) 和ζ(X) 表征了该点的频数密度F(X) 偏离该分布的幂律拟合αX-γ的程度,称之为该点的离散系数。上述4个量在本文中统称为离散系数,均为无量纲的相对量,可以用百分比表示。
2 结果在该时间序列中共获得2.99 × 105个亮点,平均每帧图上每平方角分有24.15±6.34个亮点。亮点尺度的取值范围是0″.21~76″.11。亮点逐帧总光通量的变化幅度达2个数量级。
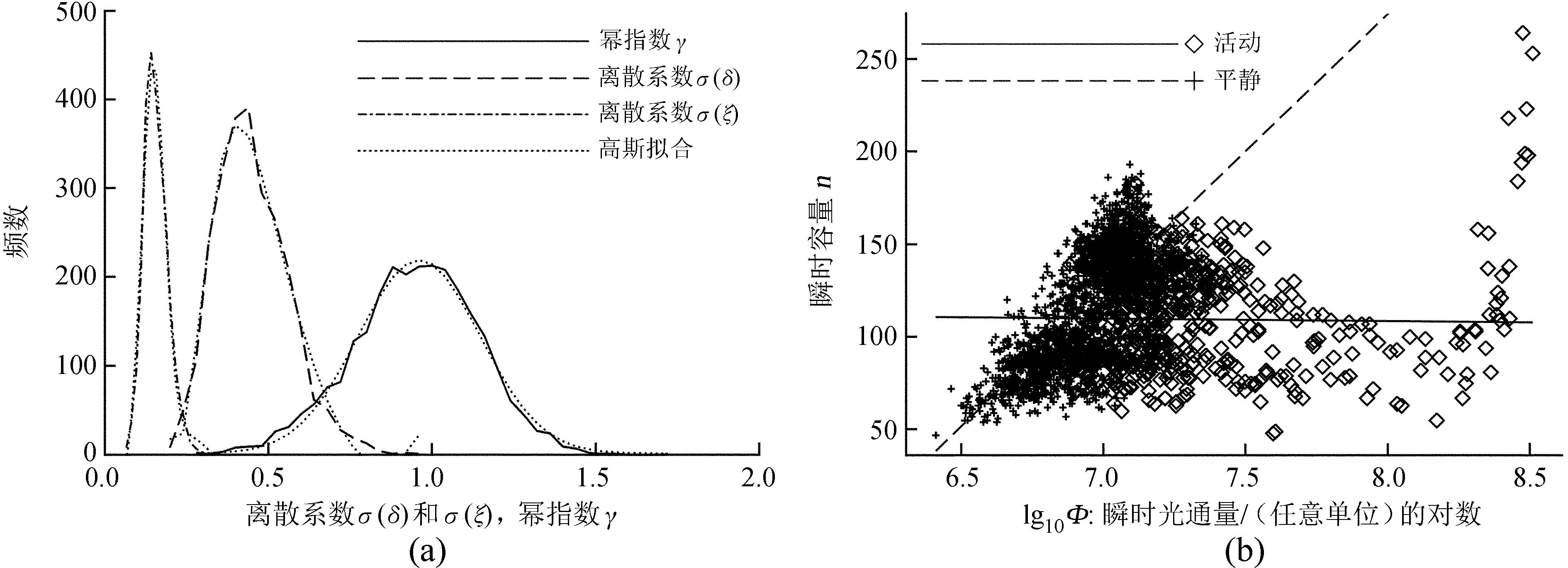
2.1 活动区亮点能量瞬时分布的幂律特征亮点的瞬时频数分布基本服从幂律分布。尽管视场中的太阳活动水平有跨多个数量级的剧烈变化,但是每一帧图像中亮点的频数分布相对幂律的离散系数只在很有限的范围内变化。图 2(a)中的虚线和点划线分别表示根据亮点尺度的瞬时分布计算的离散系数的分布。虽然离散系数σ(δ) (虚线) 的均值达到48%,但是在双对数坐标系中,频数分布与线性回归结果基本符合,离散系数σ(ζ) (点划线) 的均值为16%(表 2)。而且,σ(δ) 和σ(ζ) 均呈正态分布 (点线)。考虑到逐帧子集的容量较小 (~102),在误差允许的范围内,可以认为亮点的瞬时频数服从幂律分布。
|
| 图 2 (a) 亮点瞬时频数分布特征量的频数分布及其高斯拟合; (b) 亮点瞬时容量n与瞬时光通量Φ的关系 Figure 2 (a) Frequency distributions of the power-law index γ (solid curves), dispersion coefficients σ(δ) (dashed curves), and σ(ζ) (dash-dotted curves) of BPs′ instantaneous distributions. Dotted curves mark results of Gaussian fitting; (b) Instantaneous sample capacity n as a function of the logarithm of instantaneous light flux Φ |
| 行 | 样本a | 组数Nbin | 受测量b | log10α | γ | σ(δ) | σ(ζ) |
| 1 | 全时段实测 | 80 | 尺度L | 3.97 | 1.97 | 0.396 | 0.040 |
| 2 | 样本集 | 面积A | 3.44 | 1.10 | 0.375 | 0.069 | |
| 3 | 光通量φ | 8.59 | 1.00 | 0.504 | 0.101 | ||
| 4 | 全时段低噪声 | 80 | 尺度L | 3.92 | 2.12 | 0.239 | 0.058 |
| 5 | 样本集 | 面积A | 3.27 | 1.09 | 0.525 | 0.092 | |
| 6 | 光通量φ | 8.23 | 0.97 | 0.691 | 0.137 | ||
| 7 | 瞬时实测 | 20 | 尺度L | 0.66±0.11 | 0.97±0.19 | 0.47±0.11 | 0.16±0.04 |
| 8 | 子集 | 面积A | 0.48±0.12 | 0.55±0.11 | 0.47±0.10 | 0.17±0.04 | |
| 9 | 光通量φ | 3.25±0.53 | 0.59±0.10 | 0.46±0.10 | 0.17±0.04 | ||
| 10 | 瞬时低噪声 | 20 | 尺度L | 0.65±0.11 | 0.99±0.18 | 0.47±0.11 | 0.16±0.04 |
| 11 | 子集 | 面积A | 0.48±0.12 | 0.57±0.10 | 0.47±0.10 | 0.17±0.04 | |
| 12 | 光通量φ | 3.30±0.52 | 0.54±0.10 | 0.47±0.10 | 0.18±0.04 | ||
| (a) Lines 1-3: observed sample set; lines 4-6: low-noise sample set; lines 7-9: observed instantaneous subsets; lines 10-12: low-noise instantaneous subsets; (b) Quantities: BPs′ scale L, area A, and light flux φ | |||||||
亮点的分布基本满足幂律分布的自相似性。图 2(a)用实线绘制了亮点逐帧子集的幂指数γ(t) 的频数分布。γ近似呈正态分布,其相对变化幅度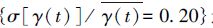
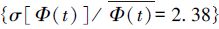
微小尺度亮点的发生是持续稳定的。亮点幂律分布的一个重要特征就是频数随着规模的增加而迅速减小,而其产生率的涨落和间歇性都随着规模的增加而增加。对亮点样本按照尺度进行分组后,使用4项指标表征各尺度区间亮点发生的稳定程度:(1) 平均数密度d;(2) 分组容量在样本容量中的比例Rn;(3) 瞬时发生率Rocc:某尺度区间的亮点在时间序列中出现帧数的比例;(4) 信号噪声比RS/N:某尺度区间亮点的瞬时数密度d(L, t) 在相邻某短时间区间 (1 h) 内的均值与标准差的比值:
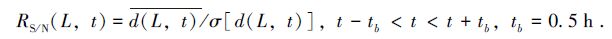
|
(10) |
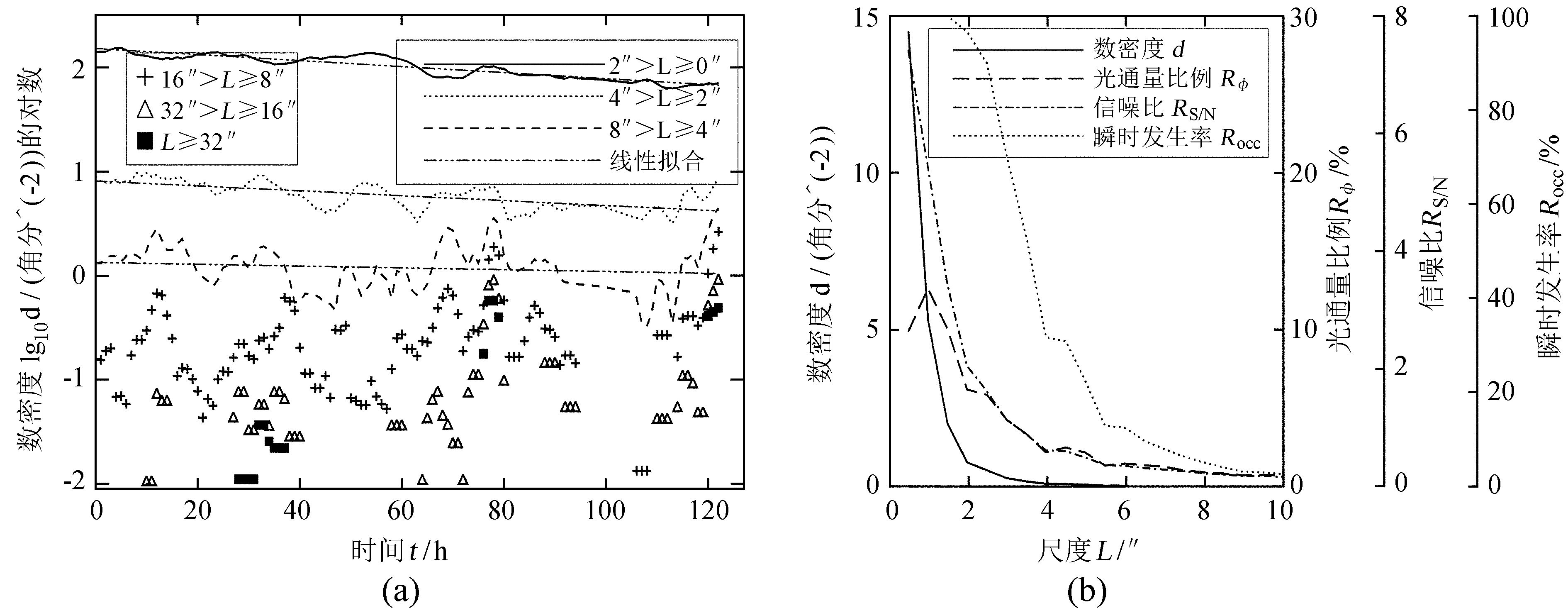
RS/N(L, t) 在观测时段内的集中趋势表征了d在短时标变化的剧烈程度。表 3(第1~4行) 列出了使用组距为2″进行等距分组后计算所得的上述4项指标。其中,尺度小于4″的亮点的瞬时发生率在99%以上,即它们在绝大多数帧的图像中出现;而尺度大于8″的亮点的瞬时发生率和信噪比都非常低。图 3(b)绘制了使用组距为0″.5进行等距分组获得的结果。它表明,亮点发生的频繁和稳定程度都随着尺度的增加而迅速减小。图 3(a)把这种区别直观地表现了出来:大尺度亮点 (符号) 的发生是间歇性的,而中小尺度亮点 (曲线) 的产生较为稳定。基于这些观察,在分析中剔除了产量低、噪声高的个体,把样本中所有尺度不大于8″的亮点作为一个子样本,以下称为低噪声样本,其容量为实测样本的99.64%。把含有L > 8″个体的瞬间称为活动瞬间;把只含有低噪声样本的瞬间称为平静瞬间。
| 行 | 统计指标a | L<2″ | 2″≤L<4″ | 4″≤L<6″ | 6″≤L<8″ | 8″≤L<10″ | 10″≤L |
| 1 | 平均数密度d/角分-2 | 22.29 | 1.31 | 0.22 | 0.07 | 0.03 | 0.06 |
| 2 | 占样本容量的比例Rn/% | 92.16 | 5.42 | 0.91 | 0.29 | 0.12 | 0.24 |
| 3 | 瞬时发生率Rocc/% | 100.00 | 99.42 | 61.46 | 26.42 | 12.55 | 14.71 |
| 4 | 信号噪声比RS/N | 9.92 | 2.77 | 1.03 | 0.56 | 0.37 | 0.49 |
| 5 | 占光通量比例Rφ/% | 35.80 | 17.43 | 7.95 | 4.71 | 3.10 | 31.01 |
| 6 | 相对增长率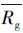 /% /% | -0.63 | -0.53 | -0.02 | 0.04 | 0.16 | 0.61 |
(a) 1.Average numerical density d/arcminute-2; 2.share in total sample capacity Rn/%; 3.instantaneous occurrence rate Rocc/%; 4. signal-to-noise ratio RS/N; 5. share in total light flux Rφ/%; 6. relative growth rate 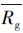 /% /% | |||||||
|
| 图 3 (a) 亮点数密度的时变。曲线/符号表示某小/大尺度区间亮点的瞬时数密度d(L, t) 的对数。直点划线表示对相应曲线的线性拟合;(b) 表征亮点产生情况的4个统计指标与尺度的关系 Figure 3 (a) Temporal variations of the logarithm of BPs′ instantaneous numerical densities d(L, t) as grouped by scale. Those of small and big BPs are marked with curves and symbols respectively. Straight lines show results of linear regression; (b) Four parameters (d, Rφ, RS/N, and Rocc) that reflect BPs′ production as functions of BPs′ scale L |
微小规模亮点的总辐射能量是相当可观的。表 3的第5行是各尺度区间的亮点产生的光通量占视场中所有亮点的总光通量的比例RΦ。尺度小于4″的亮点辐射的总光通量在样本集总光通量中占的比例达到53.23%(表 3第5行)。考虑到宽带滤光器成像仪的低时间分辨率,小尺度短时标亮点样本在被识别过程中有相当高的漏检率[22],微小尺度亮点光通量所占的实际比例有可能高于上述测量值。与此相比,最大一个尺度区间的亮点 (L≥10″) 虽然包含了多个M和X级爆发事件,其光通量只占样本总光通量的31%。因此,海量微小规模亮点持续的发生可能是加热高层大气的一种稳定而可观的能量来源。
2.3 亮点频数分布在时域中的变化小尺度亮点明显地表现出衰减的趋势。从各尺度区间亮点的数密度d与时间t的关系中,得到一个相对增长率Rg=Δd(L, t)/[d(L, t)Δt],它在观测时段内的集中趋势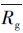
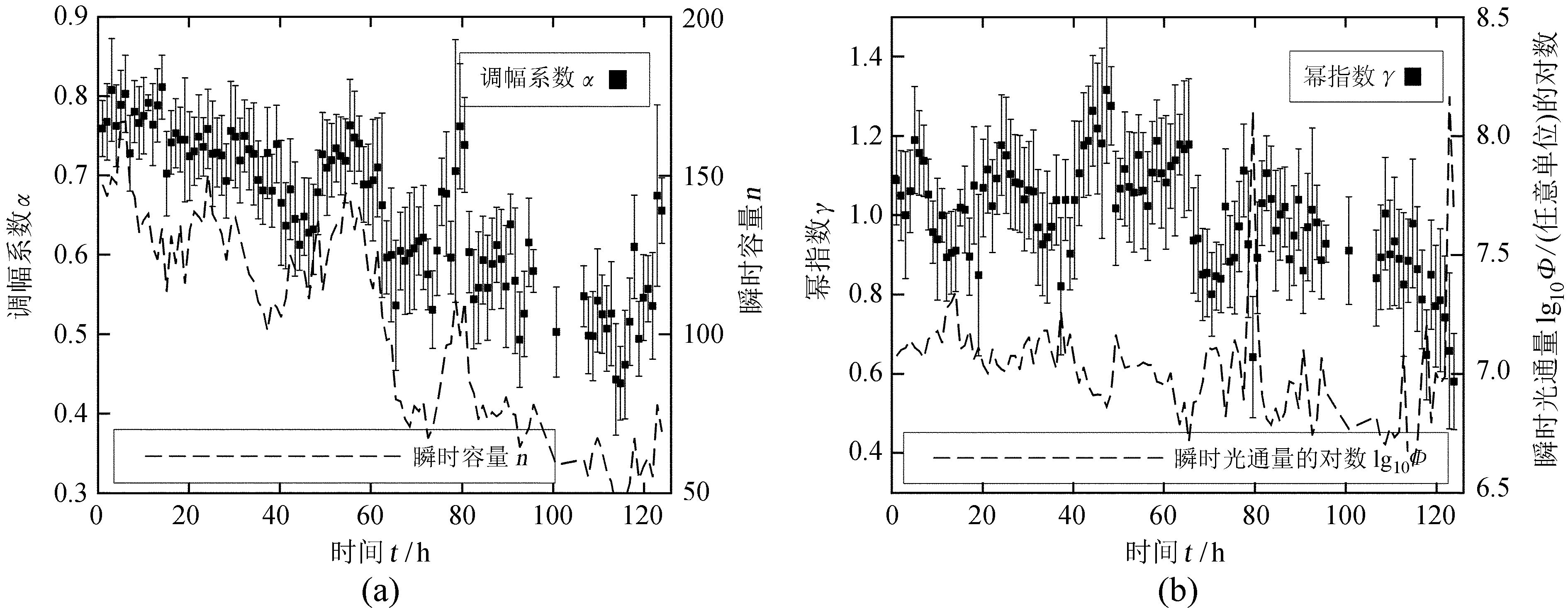
在统计分布中,活动区的衰减表现为瞬时分布的调幅指数α逐渐减小。为了研究瞬时分布的参数是否随活动区的演化而变化的问题,在时域中以小时为单位对亮点的瞬时子集进行了分组。图 4(a)和(b)分别绘制了瞬时α和γ在每小时区间的均值 (实心方块) 和标准差 (误差棒) 随时间 (横轴) 的变化。在图 4(a)中,调幅指数α基本保持随时间降低的趋势,这与瞬时容量 (虚线) 的降低一致,表征了活动区的衰减。
|
| 图 4 亮点瞬时频数分布的特征量 (纵轴) 在时域 (横轴) 中的变化。实心方块和误差棒分别表示瞬时 (a) 调幅系数α和 (b) 幂指数γ在1小时内的均值和标准差 Figure 4 Temporal variations of the parameters of BPs′ instantaneous distributions. Filled squares and error bars respectively mark the hourly averages and standard deviations of (a) α and (b) γ. Dashed curves indicate the instantaneous (a) sample capacity n and (b) logarithm of total light flux Φ |
幂指γ的变化与大规模亮点的存在有密切关系。图 4(b)中,方块表示每小时γ(t) 的均值; 虚线表示瞬时亮点子集的总光通量
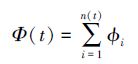
|
(11) |
的时变,Φ的突然变化主要由少数大尺度亮点造成。比较γ(t) 和Φ(t) 的变化可以看出,当活动区较为平静时,瞬时分布的γ较高;当产生大规模的亮点时,γ便迅速降低。
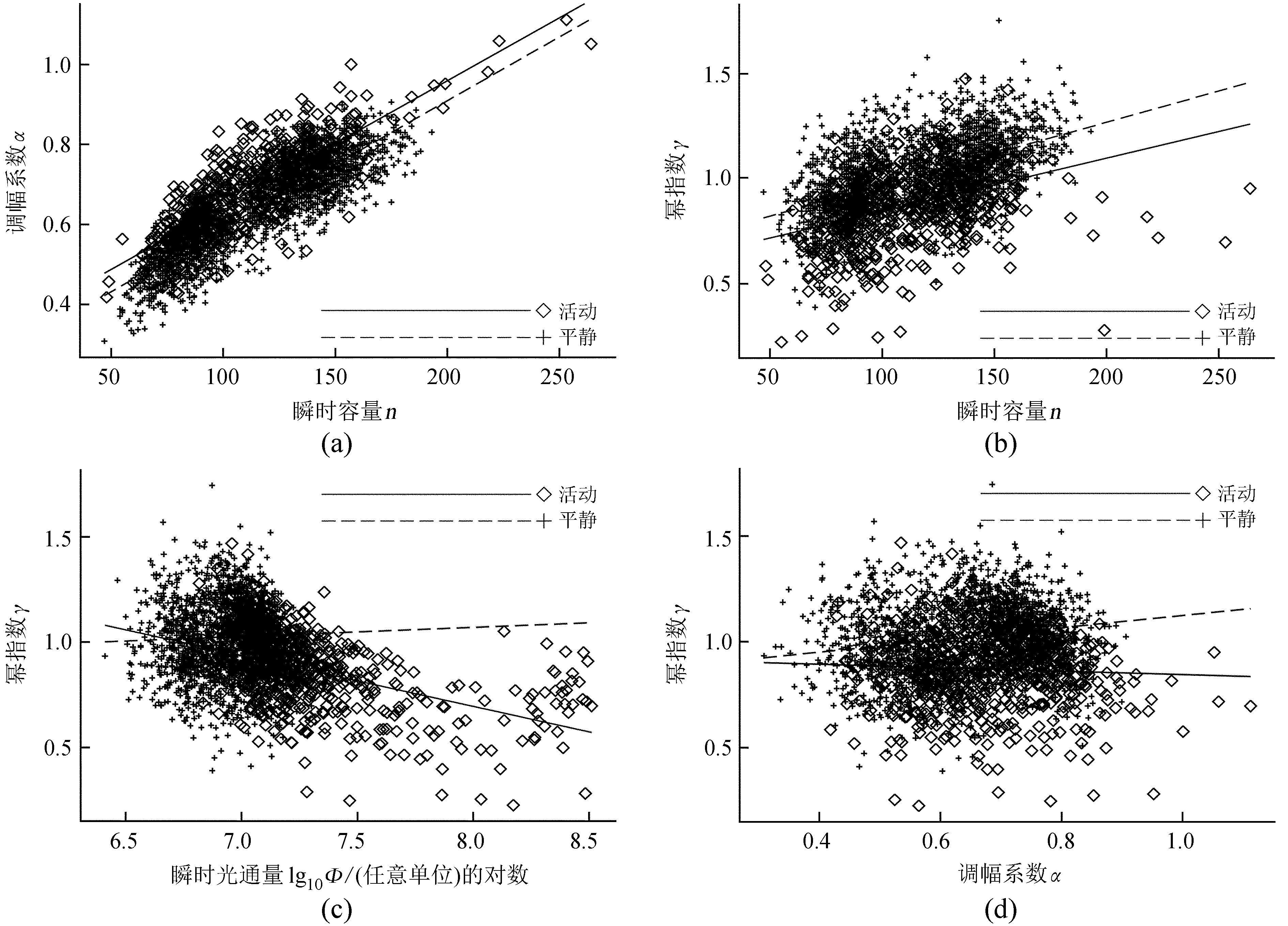
2.4 瞬时频数分布系数之间的相关性为了研究图 4中幂律参数时变的成因,分析了表征亮点瞬时分布和太阳活动水平的几个特征量的相关性,并绘制了散点图 5。平静和活动瞬间在图中分别用十字和方片标记。图 5(a)表明,调幅系数α (纵轴) 与亮点瞬时子集容量n (横轴) 之间有明确的线性关系。正如幂律关系 (1) 式,α的时变实质上体现了瞬时容量的变化。图 5(b)表明,幂指γ与瞬时容量n之间也有线性关系,当n,尤其是小尺度亮点的数目增加时,γ也相应增加。图 5(c)表明,幂指γ与瞬时总光通量Φ成反比。当活动剧烈时,Φ增加而γ降低; 而当活动区较为平静时,γ维持在较高的水平。这与图 4(b)表现的二者关系一致。图 5(d)表明,幂指γ与α是两个相对独立的参数,它们在平静和活动瞬间都没有表现出可信的相关性。
|
| 图 5 亮点瞬时频数分布各特征量之间的相关性。活动的瞬间用方片标记,平静的瞬间用十字标记。实线和虚线分别表示对活动瞬间和平静瞬间散点的线性回归 Figure 5 Correlations between the parameters of BPs′ instantaneous frequency distributions. Active and quiet moments are respectively indicated with spades and crosses. Solid and dashed lines respectively mark linear regressions for active and quiet moments |
在绘制图 4(b)和5(c)时,使用的都是低噪声样本,γ是中小尺度个体的幂指数,计算过程 (7) 式未受大尺度个体的干扰。这说明,它们所揭示的γ的突降与大尺度个体存在的关系不是一种统计效应。并不是当瞬时子集中加入了极少数大规模个体后,影响了数值计算的结果,从而造成了γ突然降低的假象。γ与太阳活动水平之间的关系是中小规模亮点分布的本征性的内在规律,爆发事件对活动区亮点的频数分布有全局性的影响,改变了瞬时分布的模式。
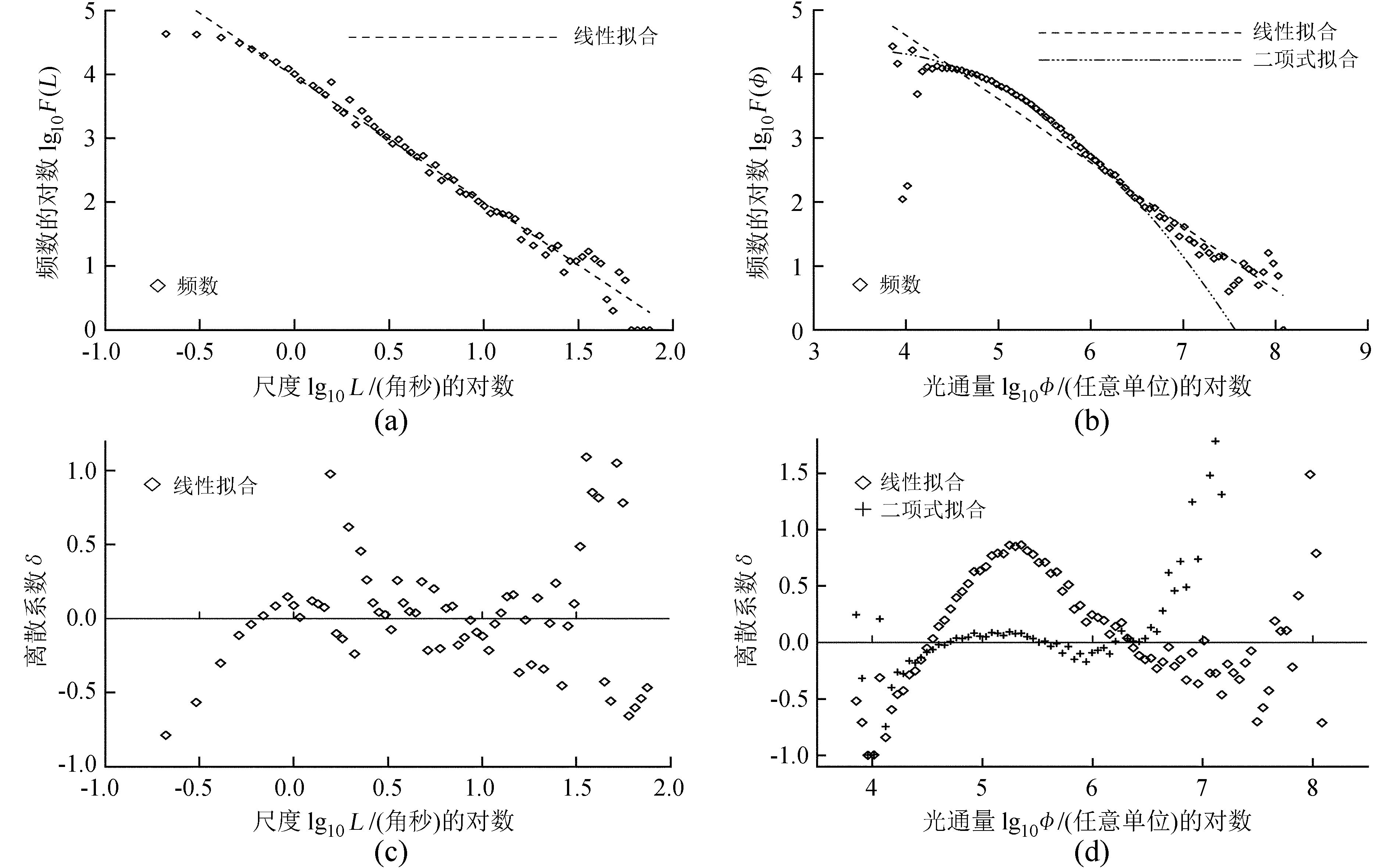
2.5 样本集的幂律分布及其累积过程亮点集的尺度服从幂律分布。图 6(a)表示在观测时段内获得的所有亮点尺度的频数分布,虚线是对实测频数的幂律拟合。图 6(c)表示实测分布 (方片) 与幂律 (水平中线) 的离散系数δ(L) 与尺度的关系。可以看出,在L取值范围的中段 (1.5≥log10L≥0.7,即32″≥L≥0″.5),频数较好地服从幂律分布,二者的离散是随机的。而在L取值范围的两端,二者有系统性的偏差。表 2的第1行列出了对样本的尺度进行拟合得出的幂律参数和离散系数,其离散系数σ(ζ) 仅为4%。
|
| 图 6 (a~b) 亮点尺度 (a) 和光通量 (b) 的频数分布。虚线和点划线分别是对实测频数的线性和二项式拟合。(c~d) 实测频数偏离幂律分布的离散系数δ (纵轴) 与亮点规模 (横轴) 之间的关系 Figure 6 (a-b) Frequency distributions of BPs′ (a) scale and (b) light flux. (c-d) Coefficients of dispersion δ as functions of BPs′ (c) scale and (d) light flux. Dashed lines and spades mark results of linear regressions; crosses and dash-dotted curves mark results of binomial regressions |
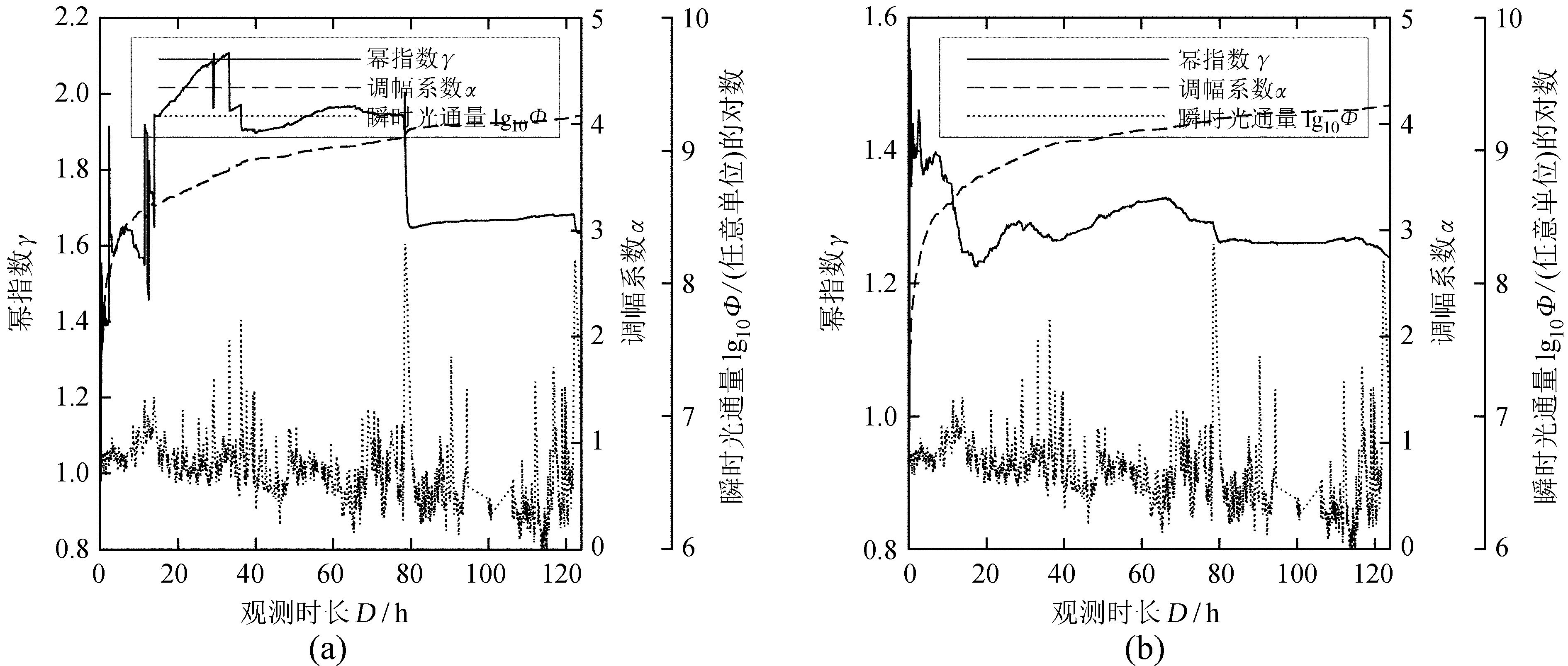
但是,上述亮点样本的幂律分布并不是稳定的,在为期124小时的观测时间内γ没有收敛。假设某观测始于该时间序列的起点 (t0=2006-12-09T20: 02Z),终止于时间序列中的某时刻t0+D,则可以计算从观测时段获得的亮点子样本的幂律参数与观测时长D的关系。在图 7中,任一时刻的γ (实线) 和α(虚线) 描述了在t0~t0+D中累积的亮点样本尺度的幂律分布。图中还绘制了代表视场中太阳活动水平的瞬时总光通量Φ(t) (点划线) 以作为参考。图 7(a)和(b)分别使用实测样本和低噪声样本。由图 7(a)可知,α随着样本容量的累积而单调增加。当观测时段很短时 (曲线左端),γ有大幅度的震荡; 当活动水平较为平静时,γ逐渐增高; 当发生大规模事件时,样本集中被注入了小γ的瞬时子集,造成累积γ的急剧降低。在D的取值范围内,γ一直处于锯齿状变化之中,没有收敛。可以推测,即便进行更长时标的观测,样本中也会不定期地加入大规模的个体,累积γ也有可能发生突然的变化。因此,实测样本集的γ是一个在观测积累中不断变化的过程,基于该样本所得到的γ值 (表 2第1~3行) 只有有限的意义,在该活动区的统计结果中也无法判断γ的长时标走向。
|
| 图 7 累积亮点样本集的频数分布各参数 (纵轴) 随观测时长 (横轴) 的变化。图 (a) 和 (b) 所统计的分别是实测样本和低噪声样本 Figure 7 Variations of α (dashed curves) and γ (solid curves) of a partial BP sample set accumulated during a hypothetical observation time D. Panels (a) and (b) are plotted respectively with observed and low-noise samples. Dotted curves show the temporal variations of log10Φ |
为了减小少量大尺度个体对子样本γ的影响,使用低噪声样本重复上述计算并绘制了图 7(b)。在去除大尺度个体之后,γ虽没有收敛,但其变化幅度随着容量的增加而逐渐减小。可以认为,低噪声样本的γ值 (表 2第4~6行) 对观测时段的选取不很敏感,因而有较高的可信度,能较客观地反映亮点的频数分布特征。
在双对数坐标系中,亮点的光通量Φ和面积A基本服从二项式分布。从实测样本集的光通量的频数分布 (图 6(b)) 及其与幂律的离散δ(φ)(图 6(d)) 可以看出,二者有系统性的偏差。对小容量的瞬时亮点子集而言,该偏差可以忽略,线性 (幂律) 拟合可以代表其频数分布的主要特征。但此偏差对大容量的样本集来说不能忽略,幂律分布不能准确地表示其分布。对面积和光通量使用二次项拟合
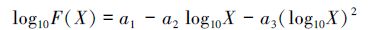
|
(12) |
后 (图 6(d)中十字),大大减小了此偏差。
2.6 误差分析对于中等规模的亮点, 获得的样本比较完整,频数曲线的中段较为光滑,较好地体现了亮点按照尺度呈幂律分布的关系。但是,实测频数分布曲线的两端与幂律分布的偏差较大。这些偏差既有物理本质的因素,也有观测造成的系统误差。研究中的误差主要产生于对亮点的识别过程。
亮点频数分布的右端代表样本中规模较大的级别 (≥10″)。图 6中各分布的右端均有较大的噪声,并与幂律分布有明显的偏差,这可能有3方面的原因。(1) 这种偏差有可能是本征性的,规模大的耀斑有可能遵守指数分布而不是幂律分布。受样本容量的限制,在本文的数据基础上尚无法判断这种可能性的真伪。(2) 由于单个活动区大规模耀斑的数目非常有限,频数参差不齐,不能获得可信的频数密度。若要获得大耀斑的准确统计规律,需要对大量活动区进行统计,大幅度增加样本容量。但是,由于幂律分布的无标度性,无论样本容量有多大,其中最大规模的个体数目总是很有限的,所以频数分布的最右端也总是较为离散。(3) 大耀斑效应。发生大耀斑时,对视场中各种尺度亮点的频数统计都不准确。(a) 对于有一部分面积超出视场的大尺度亮点,所测量的内容比实际内容小。这在一定程度上造成了图 6中曲线的右端比幂律分布高并突然终止的情况。如果使用全日面观测资料,可以基本消除此类误差。(b) 多个临近的亮点区域可能发生粘连并被识别为同一个区域。改进本区域识别算法的难点和目标是使其能够在降低大尺度增亮区域噪声的同时又能保留小尺度区域的精细结构,从而对尺度迥异的亮点进行同等准确的测量。(c) 由于所使用的观测数据在爆发区域常出现大面积饱和现象,低估了其光通量,实测亮点光通量的分布规律与面积的分布规律非常相似,并不是真实分布的准确反映。
各频数分布曲线的左端代表尺度小、时标短的亮点,它们的频数密度比幂律拟合值都明显偏低,且二者的差异随着规模的减小而增加,如图 6(c)和(d)。例如,实测样本中最小尺度的亮点 (~0″.24) 的频数只有幂律拟合值的22%。这主要由采样过程中的误差造成。首先,该时间序列的低时间分辨率导致了低采样率。由于该时间序列的间隔时间 (120 s) 较长,对海量小尺度、短时标个体有较高的漏检率[22]。其次,大耀斑效应也影响了对亮点的统计。散点图 2(b)表示瞬时容量n与瞬时光通量Φ的关系。活动瞬间 (方片) 并不遵守在宁静瞬间 (十字) 表现的线性关系 (虚线),其瞬时容量偏小,这可能因为大耀斑的发生掩盖了临近的小尺度亮点。该误差对2.3~2.5节中的分析也可能有一定影响。
3 结论与展望 3.1 结论本文使用二维区域识别算法,在太阳光学望远镜对NOAA 10930所观测的Ca Ⅱ H时间序列中,获得了一个容量为2.99 × 105的低色球层亮点样本,分析了其瞬时频数分布的基本特征、时变规律和累积样本分布。主要结果如下:
(1) 亮点的尺度服从幂律分布。样本尺度的实测频数与幂律的离散系数σ(ζ) 仅为4%。亮点的瞬时分布也基本符合幂律分布并满足自相似性;
(2) 该实测样本尺度的γ为1.97,剔除大耀斑之后的低噪声样本的γ为2.12;
(3) 在跨度为124小时的观测时间内,样本集的γ并没有收敛。γ是一个在观测积累中呈锯齿状变化的过程:在平静时段缓慢升高,在活动瞬间突然降低;
(4) 累积γ如此变化的原因是亮点瞬时分布的幂指γ(t) 与瞬时子集的总光通量Φ(t) 呈反比。在样本中剔除大尺度 (L > 8″) 个体后,仅含有中、小尺度亮点的低噪声样本仍服从上述规律。太阳活动不仅产生中、大尺度的增亮区域,还对亮点的频数分布产生全局性的影响,引起瞬时γ的降低;
(5) 小尺度亮点的瞬时数密度及调幅指数α随着活动区的衰减而降低;
(6) 亮点的产生率及其信噪比随着尺度的增加而减小。海量微小规模亮点持续的发生可能是加热高层大气的一种稳定而可观的能量来源,例如,尺度小于4″的亮点产生的光通量在样本总光通量中占的比例达到了53.23%。
3.2 展望以下工作将有助于进一步揭示亮点分布特征的统计规律和形成机制。
(1) 使用高时、空分辨率数据对小规模亮点的分布规律进行准确统计。历史上对亮点幂律分布的观测统计中,频数分布在低端的拐点往往由观测手段的阈值造成,并不是物理实质的反映。本文中,微小规模亮点的实测频数的确小于幂律分布,但是由于对小规模亮点获取的信息很不完全,无法对微小亮点频数与幂律的本征性偏离进行判断,也难以进一步估算其在大气加热中的贡献。只有使用高时间分辨率和衍射极限更小的观测设备,方能更准确地获得小规模亮点的分布规律,进一步了解微小规模能量释放在日冕加热中的作用。
(2) 对低层亮点和磁场凝聚的空间分布进行比较。活动区的浮现、爆发和衰减,实质上是磁场结构和能量上传和扩散的过程。而宁静区没有大尺度磁场凝聚的产生和消失。结合光球磁场资料中磁场凝聚的形成和衰减过程,分析活动区不同演化阶段以及宁静区亮点的分布特征和演化方式,可以深入对磁场演化和能量传输过程的理解。
(3) 对低层大气中各波段亮点的分布规律进行比对研究。目前对高层大气中活动能量幂律分布的研究已经覆盖了较宽广的波段和时标[11],但是对低层大气中的亮点,尤其是色球层和过渡区亮点,所掌握的宏观分布规律还很有限。而光球亮点是具有特征尺度的[21, 37],并不满足无标度条件。对低层大气亮点分布规律的多波段比对研究,有助于了解能量释放机制随高度的变化。例如,亮点服从幂律分布的最低层次是什么?为什么能量的分布规律在该高度发生了变化?
(4) 使用全日面、长时标的数据分析亮点分布规律随太阳活动水平的变化。本文仅在一个衰减的活动区狭窄的时空范围内,对亮点幂律分布随太阳活动的时变进行了有限的分析。在全日面、跨太阳周的范围内对亮点进行统计,一方面可以研究活动区的磁场演化影响日面上亮点空间分布的动态过程,另一方面可以研究幂律分布特征随太阳周的长时标变化规律。
致谢:
谨以此文缅怀杨志良教授 (1965~2016)。“日出”卫星是由日本ISAS/JAXA主持,日本国家天文台、美国宇航局、英国STFC协作完成,并和欧洲空间局、挪威NSC共同操作的太阳观测设备。本研究使用了IDL语言、SSW软件包、ADS文献库和Kubuntu操作系统。
| [1] | Datlowe D W, Elcan M J, Hudson H S. OSO-7 observations of solar X-rays in the energy range 10-100 keV[J]. Solar Physics , 1974 , 39 (1) : 155 –174. |
| [2] | Lin R P, Schwartz R A, Kane S R, et al. Solar hard X-ray microflares[J]. The Astrophysical Journal , 1984 , 283 (1) : 421 –425. |
| [3] | Dennis B R. Solar hard X-ray bursts[J]. Solar Physics , 1985 , 100 (1) : 465 –490. |
| [4] | Bai T. Variability of the occurrence frequency of solar flares as a function of peak hard X-ray rate[J]. The Astrophysical Journal , 1993 , 404 : 805 –809. DOI: 10.1086/172335 |
| [5] | Crosby N B, Aschwanden M J, Dennis B R. Frequency distributions and correlations of solar X-ray flare parameters[J]. Solar Physics , 1993 , 143 (2) : 275 –299. DOI: 10.1007/BF00646488 |
| [6] | Shimojo M, Shibata K. Occurrence rate of microflares in an X-ray bright point within an active region[J]. The Astrophysical Journal , 1999 , 516 (2) : 934 –938. DOI: 10.1086/apj.1999.516.issue-2 |
| [7] | Veronig A, Temmer M, Hanslmeier A, et al. Temporal aspects and frequency distributions of solar soft X-ray flares[J]. Astronomy & Astrophysics , 2002 , 382 (3) : 1070 –1080. |
| [8] | Su Y, Gan W Q, Li Y P. A statistical study of Rhessi flares[J]. Solar Physics , 2006 , 238 (1) : 61 –72. DOI: 10.1007/s11207-006-0156-8 |
| [9] | McIntosh S W, Gurman J B. Nine years of EUV bright points[J]. Solar Physics , 2005 , 228 (1) : 285 –299. |
| [10] | Alipour N, Safari H. Statistical properties of solar coronal bright points[J]. The Astrophysical Journal , 2015 , 807 (2) : 175 –183. DOI: 10.1088/0004-637X/807/2/175 |
| [11] | Aschwanden M J, Crosby N B, Dimitropoulou M, et al. 25 years of self-organized criticality: solar and astrophysics[J]. Space Science Reviews , 2016 , 198 (1) : 47 –166. |
| [12] | Wheatland M S, Sturrock P A. Avalanche models of solar flares and the distribution of active regions[J]. The Astrophysical Journal , 1996 , 471 (2) : 1044 –1048. |
| [13] | Wheatland M S. Flare frequency-size distributions for individual active regions[J]. The Astrophysical Journal , 2000 , 532 (2) : 1209 –1214. DOI: 10.1086/apj.2000.532.issue-2 |
| [14] | Perrone D, Dendy R O, Furno I, et al. Nonclassical transport and particle-field coupling: from laboratory plasmas to the solar wind[J]. Space Science Reviews , 2013 , 178 (2) : 233 –270. |
| [15] | Hale G E. Solar magnetism[J]. Nature , 1935 , 136 (3444) : 703 –705. DOI: 10.1038/136703a0 |
| [16] | McIntosh S W, Wang X, Leamon R J, et al. Deciphering solar magnetic activity I: on the relationship between the sunspot cycle and the evolution of small magnetic features[J]. The Astrophysical Journal , 2014 , 792 (2) : 12 –30. |
| [17] | Rieger E, Kanbach G, Reppin C, et al. A 154-day periodicity in the occurrence of hard solar flares?[J]. Nature , 1984 , 312 : 623 –625. DOI: 10.1038/312623a0 |
| [18] |
赵明宇, 陈军权, 刘煜, 等. 太阳活动峰年和谷年期间黑子群与耀斑的统计分析[J]. 中国科学:物理学力学天文学
, 2014 , 44 (1) : 109 –120 Zhao Mingyu, Chen Junquan, Liu Yu, et al. Statistical analysis of sunspot groups and flares for solar maximum and minimum[J]. Scientia Sinica: Physica Mechanica Astronomica , 2014 , 44 (1) : 109 –120. |
| [19] |
牛俊, 方涵先, 翁利斌. 太阳活动与热层大气密度的相关性研究[J]. 空间科学学报
, 2014 , 34 (1) : 73 –80 Niu Jun, Fang Hanxian, Weng Libin. Correlation between solar activity and thermospheric density[J]. Chinese Journal of Space Science , 2014 , 34 (1) : 73 –80. |
| [20] | Lu E T, Hamilton R J. Avalanches and the distribution of solar flares[J]. The Astrophysical Journal Letters , 1991 , 380 (2) : L89 –L92. |
| [21] | Abramenko V, Yurchyshyn V, Goode P, et al. Statistical distribution of size and lifetime of bright points observed with the new solar telescope[J]. The Astrophysical Journal Letters , 2010 , 725 (1) : L101 –L105. DOI: 10.1088/2041-8205/725/1/L101 |
| [22] |
李小波, 杨志良, 张洪起. 基于三维区域标记对太阳活动区低色球层亮点的统计分析[J]. 北京师范大学学报 (理)
, 2016 , 52 (5) : 542 –549 Li Xiaobo, Yang Zhiliang, Zhang Hongqi. Distribution of low-chromospheric brightpoints in a solar active region as observed by region-labeling[J]. Journal of Beijing Normal University (Natural Science) , 2016 , 52 (5) : 542 –549. |
| [23] |
冯恒强, 曹行健. 行星际磁通量绳尺度的幂律谱分布[J]. 天文研究与技术——国家天文台台刊
, 2010 , 7 (1) : 1 –7 Feng Hengqiang, Cao Xingjian. Power-law distribution of scale lengths of interplanetary magnetic flux ropes[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China , 2010 , 7 (1) : 1 –7. |
| [24] | Wheatland M S. Evidence for departure from a power-law flare size distribution for a small solar active region[J]. The Astrophysical Journal , 2010 , 710 (2) : 1324 –1334. DOI: 10.1088/0004-637X/710/2/1324 |
| [25] | Parker E N. The sun: the ultimate challenge to astrophysics[J]. Advances in Space Research , 1998 , 21 (1-2) : 267 –274. DOI: 10.1016/S0273-1177(97)00982-4 |
| [26] | Ilonidis S, Zhao J, Kosovichev A. Detection of emerging sunspot regions in the solar interior[J]. Science , 2011 , 333 (6045) : 993 –996. DOI: 10.1126/science.1206253 |
| [27] | Bak P, Tang C, Wiesenfeld K. Self-organized criticality: an explanation of the 1/f noise[J]. Physical Review Letters , 1987 , 59 (4) : 381 –384. DOI: 10.1103/PhysRevLett.59.381 |
| [28] | Albert R, Barabási A L. Statistical mechanics of complex networks[J]. Reviews of Modern Physics , 2002 , 74 (1) : 47 –97. DOI: 10.1103/RevModPhys.74.47 |
| [29] | Daly E, Porporato A. Effect of different jump distributions on the dynamics of jump processes[J]. Physical Review E , 2010 , 81 (6) : 061133 –1. DOI: 10.1103/PhysRevE.81.061133 |
| [30] | Zirin H. The magnetic structure of plagues[C]//Athay R G. Chromospheric fine structure, volume 56 of IAU Symposium. Boston: Reidel, 1974: 161-175. |
| [31] | Li X B, Yang Z L, Zhang H. Formation of pores associated with the inflow of moving magnetic features[J]. The Astrophysical Journal , 2015 , 807 (2) : 160 –174. DOI: 10.1088/0004-637X/807/2/160 |
| [32] | Hudson H S. Solar flares, microflares, nanoflares, and coronal heating[J]. Solar Physics , 1991 , 133 (2) : 357 –369. |
| [33] | Tu C Y, Marsch E. MHD structures, waves and turbulence in the solar wind: Observations and theories[J]. Space Science Reviews , 1995 , 73 (1) : 1 –210. |
| [34] | Suzuki T K, Inutsuka S I. Solar winds driven by nonlinear low-frequency Alfvén waves from the photosphere: Parametric study for fast/slow winds and disappearance of solar winds[J]. Journal of Geophysical Research , 2006 , 111 (A6) : 06101 . DOI: 10.1029/2005JA011502 |
| [35] |
方锦清, 汪小帆, 郑志刚, 等. 一门崭新的交叉科学:网络科学 (上)[J]. 物理学进展
, 2007 , 27 (3) : 239 –343 Fang Jinqing, Wang Xiaofan, Zheng Zhigang, et al. New interdisciplinary science: networks science[J]. Progress in Physics , 2007 , 27 (3) : 239 –343. |
| [36] |
刘艳霄, 杨云飞, 林隽. 太阳光球磁亮点的识别算法[J]. 天文研究与技术
, 2014 , 11 (2) : 145 –150 Liu Yanxiao, Yang Yunfei, Lin Jun. A region-growth algorithm to recognize magnetic bright spots in the solar photosphere[J]. Astronomical Research & Technology , 2014 , 11 (2) : 145 –150. |
| [37] | Crockett P J, Mathioudakis M, Jess D B, et al. The area distribution of solar magnetic bright points[J]. The Astrophysical Journal Letters , 2010 , 722 (2) : 188 –193. |
| [38] | Kalkofen W. Oscillations in chromospheric network bright points[J]. The Astrophysics Journal , 1997 , 486 (2) : L145 –L148. |
| [39] | Bocchialini K, Vial J C, Einaudi G. Statistical analysis of a bright point observed simultaneously in two chromospheric and transition region lines by SUMER[C]//Wilson A, Fifth SOHO workshop: The corona and solar wind near minimum activity, 1997, 404: 211-215. |
| [40] | Pérez-Suárez D, Maclean R C, Doyle J G, et al. The structure and dynamics of a bright point as seen with Hinode, SoHO and TRACE[J]. Astronomy & Astrophysics , 2008 , 492 (2) : 575 –583. |
| [41] |
卢小广. 统计学教程[M].
北京: 清华大学出版社. 2005, 33-36.
|
| [42] | Newman M E J. Power laws, Pareto distributions and Zipf's law[J]. Contemporary Physics , 2005 , 46 (5) : 323 –351. |



