2. 中国科学院国家天文台, 北京 100012
2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China
1923年世界上第1台光学天象仪在德国诞生,在其后的几十年里,光学天象仪一直是天象厅的主角。随着数字视频技术的诞生和快速发展,数字影院不断投入商业运行,有取代胶片放映机的趋势。同样在天文科普场馆, 数字视频技术也扮演越来越重要的角色。1983年,美国益世公司(E & S)的数字式投影系统Digistar问世[1]。以此为标志,数字视频技术正式走进天象厅,开启了数字天象厅时代。
传统天象厅主要用各种光学天象仪模拟星空, 在半球型天幕上演示人们在地球上不同位置看到的各种天体及其运行情况, 如:四季星空、太阳的东升西落、行星在各自轨道中运行等。但是传统天象厅在某些方面也存在不足,比如展示的内容相对有限,天象仪由一系列机械部件组成,结构复杂,后期升级维护比较麻烦。
数字天象厅不仅可以像光学天象厅那样演示星空,还可以播放高分辨率的球幕视频。通过视频和球幕的立体沉浸感,带人们感受各种天文奇观,使观众真正做到“静坐一室,遨游太空”,大大扩展了天象厅的科普教育功能①。
① http://www.ict.ac.cn/kxcb/kxr/201009/t20100907_2945827.html
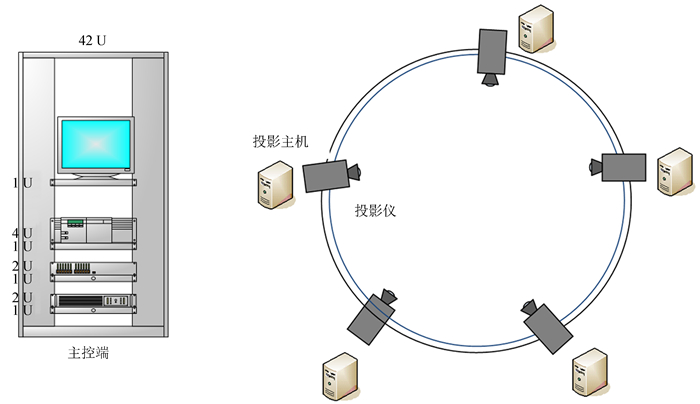
数字天象厅系统所用的投影显示技术称为球幕投影技术。球幕投影是指使用一台或多台投影机,在球形屏幕上投影出完整连续的画面。球幕投影可以表现高分辨率、大视角范围的显示效果,给观众带来新颖的视觉体验。投影仪数目由球幕的直径大小决定,一般来说对于直径较小(6 m以下)的球幕,投影显示部分可以用一台装有鱼眼镜头的投影仪完成。对于直径较大的球幕(6 m以上)则需要采用多台投影仪投影拼接的显示方式[2]。对于球幕直径大小和所采用的投影方式没有严格界定。目前国内多数大型天象厅和球幕剧场采用多投影仪拼接显示的方式,如图 1。
|
| 图 1 多投影拼接构建示意图 Figure 1 Schematic diagram of these multi-projectors |
2008年北京天文馆老馆经过两年的改造后重新开放。天象厅内部采用德国蔡司公司“宇宙9型”光学天象仪的同时,配备了当时世界上分辨率最高的全天域数字投影系统。这套系统用6台数字投影机进行数字图像拼接,24台高性能图形计算机并行处理运算任务。实时运算得到的数字星空图像能够覆盖整个球幕,形成一个总体分辨率为7 800 × 7 800的球幕影像。这套超高分辨率数字投影系统能够对光学天象仪形成完美的补充,使天象厅内天球效果更加清晰,接近旷野的自然状态,为观众提供更为真实的视觉体验②。
② http://wiki.astron.ac.cn/wiki/天象厅
2014年中国高校首座万维天文望远镜(World Wide Telescope, WWT)互动式数字天象厅在北京师范大学建成③。万维天文望远镜是一套纯数字的互动式天象厅软件和科学数据可视化平台,它把美国宇航局、哈勃空间望远镜、斯隆数字巡天等世界上各大天文望远镜、天文台、探测器的观测数据融合成一个无缝的数字宇宙④,并通过极富创新性的数据可视化方式呈现。在天象厅中通过球幕投影的方式,把真实的宇宙立体地呈现给观众。这座天象厅既可以用万维天文望远镜软件进行天文演示又可以播放球幕视频,是一座功能强大、理念先进的数字天象厅。
③ http://astrowww.bnu.edu.cn/CN/index.php/2010-04-29-00-39-09/223-wwt
④ http://wwt.china-vo.org/home.htm
对于采用多个投影仪的万维天文望远镜互动式天象厅和其他数字天象厅,所采用的球幕投影技术关键是通过多台投影仪图像拼接获得覆盖整个球幕的完整画面。但是目前许多球幕多投影显示技术在构建过程中比较繁琐,自动化程度不高。如果在使用过程中投影仪受外界环境的影响位置发生移动,就需要重新进行复杂的校正过程。
本文针对以上问题提出了面向中小型球幕基于鱼眼相机的球幕投影自动校正技术,通过自动的几何校正、亮度校正、颜色校正等关键技术获得大屏幕、高分辨率、画面均匀统一的输出图像。本文第2节对该技术的核心步骤提出相关方案,并对方案原理进行详细论述。第3节对该技术进行具体的实施验证。
2 数字天象厅投影拼接关键技术数字天象厅投影显示的关键技术为几何校正、亮度校正、颜色校正。几何校正主要解决图像的画面连续性问题。例如一条连续直线需要跨越多台投影仪共同显示,那么通过这几台投影仪的拼接,显示在球幕上时仍然保持为一条球面直线。亮度校正主要解决拼接后图像亮度连续性问题,使覆盖在球幕上各区域图像的亮度基本一致。颜色校正主要解决拼接后图像颜色连续性的问题,使各台投影仪输出在球幕上的图像颜色基本一致。
2.1 几何校正原理几何校正主要包括对单个投影画面的图像畸变校正和多个投影画面之间的对齐校正。几何校正是通过几何变换实现输出图像在方向、尺寸等方面的变化,使得各个投影仪共同输出一幅完整画面。投影仪在球幕上投影时,由于球幕是一个曲面,球幕上不同位置的画面产生的形变各有不同,靠近球幕边缘画面拉伸比较严重。同时为了实现无缝拼接,相邻投影仪的投影部分要相互重叠一定的区域,这就需要对投影仪输出画面进行几何校正。
许多研究者对平面多投影输出几何校正进行了相关研究。文[3]提出使用一个摄像头,通过计算投影空间、摄像空间和显示空间的对应性实现多个投影仪的几何校正的方法。文⑤介绍了针对平面规则投影幕的投影仪图像自动校正技术。上述方法称为参数化方法,即通过投影和拍照提取若干组特征点计算对应性矩阵,从而获得投影仪坐标系和屏幕坐标系的对应关系⑥。参数化方法适用于特征点组数不多的平面投影校正,平面投影下图像无扭曲变形,比较规律,用不多的几组特征点就可以刻画出投影仪的位置信息。如果所取特征点组数过多,相关计算非常复杂。对于球形投影幕来说,投影仪的图像在屏幕上发生形变,这就需要设置尽可能多的特征点精确刻画形变信息,很难通过参数化的计算方法获得投影仪坐标系和屏幕坐标系的对应关系。针对参数化方法的缺点和球幕的特点提出基于鱼眼镜头相机的非参数方法实现几何校正,该方法不用求解对应性矩阵,避免了多特征点情况下复杂的计算。
⑤ http://dl.acm.org/citation.cfm?id=602151
⑥ https://cseweb.ucsd.edu/classes/sp13/cse252B-a/HZ2eCh2
非参数化方法的核心是投影仪按一定编码规律向球幕投射特征点,特征点由一簇像素组成,通过较大的特征点密度刻画投影仪图像的形变和位置信息。用相机对特征点图像进行拍照,通过所用的编码规律把照片上的特征点与投影仪所投特征点一一对应。然后通过分析照片上特征点的坐标位置信息就得到投影仪在整个屏幕的位置和形变信息。照片上特征点的范围代表投影仪的相对投影范围,照片上特征点之间位置的相对变化代表投影仪图像的变化信息。获得两坐标系特征点的对应关系和坐标值,就可以使用OpenGL纹理映射的方法,把要输出的图像依据特征点坐标位置相关信息进行纹理贴图,即可获得每台投影仪输出图像,实现几何校正。
本文把特征点大小降低至像素级别,即投影仪的每个像素都作为特征点,达到特征点密度最大化。设计合理的像素编码算法,使得投影仪中每个像素点都能在照片中对应到相应的位置,进而准确刻画出投影仪位置和形变信息就成了非参数化方法的关键。
投影仪的每个像素可以由其横纵坐标值唯一确定,每个像素都唯一对应一个二进制坐标值(s,t)。针对每个像素的二进制坐标值分别进行编码,形成一定规律显示的编码图像,然后用相机拍照。照片中该投影仪的显示区域会出现这种规律的编码图像,即照片中某些像素也符合上面的编码规律,根据编码规律可以计算照片中这些像素在投影仪坐标系中对应的像素点的坐标,则相机坐标中的相关像素点和投影仪坐标系中的像素点相对应。由于投影仪分辨率和投影仪投影区域在照片中所占分辨率的差异,投影仪坐标系的有些像素没有找到相机坐标系中确实存在的对应像素,根据相邻像素所对应相机坐标系像素的坐标值进行插值,求取其所对应的“虚拟像素”的坐标值。两坐标系中对应的像素点在各自坐标系的坐标值是进行纹理映射的数据基础。相关原理步骤如下:
(1) 获取像素点编码图像
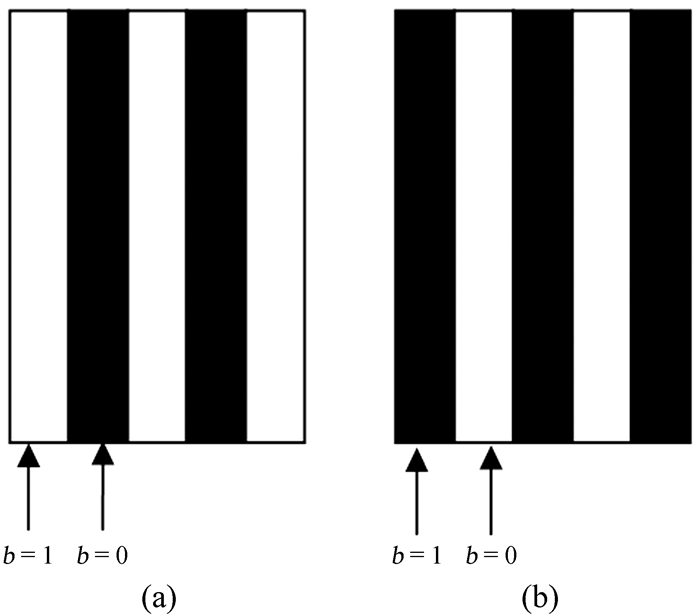
以投影仪分辨率为1 280 × 800,像素A(s,t),s、t为二进制数,为例:投影仪分辨率为1 280 ×800(10 100 000 000 × 1 100 100 000),那么横坐标为11位二进制数,纵坐标为10位的二进制数。对于横坐标值的二进制数s,对其每一位b(0~10)分别编辑一幅灰度图像,共11幅,规则如下:从左边第1位起如果b=1,那么像素A在对应的图像中显示为纯白(亮度为255);如果b=0,那么像素A在对应的图像中显示为纯黑(亮度为0)。所有位的对应图像显示完毕后,再依次显示与上述图像“互逆”的图像。即如果b=1,则该像素在对应图像中显示纯黑;b=0则显示为纯白⑦。两次显示顺序相同的图像视为一组“互逆”图像,编号为0~10组,第n组图像对应s的第n位。投影仪投射出的画面为一幅幅黑白相间的纵向条带状图像(图 2)。
⑦ http://mathworld.wolfram.com/GrayCode.html
|
| 图 2 对横坐标编码时一组互逆图像示意图 Figure 2 A group of inverse images when coding the horizontal ordinate (a) b=1, the brightness=255; b=0, the brightness=0; (b) the inverse image of (a) |
对于纵坐标的二进制值t做同样处理,得到10幅横向显示的条纹图像。
(2) 投射在球幕上的每一幅图像分别用鱼眼相机拍照并对照片作去噪处理,所拍摄的照片用于下一步求取两坐标系中像素的对应关系。
(3) 相机坐标系像素到投影仪坐标系像素对应关系求取。
按照第(1)步的编码规律,把相机坐标系(U, V)中的像素点到投影仪坐标(S, T)中的像素点对应关系R[(U, V)→(S, T)]分解为横坐标S上的对应关系Rs和纵坐标T上的Rt分别求取,Rs和Rt分别表示一个二进制数。最后再整合为R,R表示由Rs和Rt组成的坐标。
首先求Rs。Rs在上述步骤中对应11组“互逆”图像,0~10组图像分别用来求取S的0~10位上的0或1。遍历每组“互逆”图像的所有像素,把每组“互逆”图像对应像素亮度相减,如图 2中为包含(a)的照片像素亮度值减去包含(b)的照片对应像素亮度值。分析差值用于求取对应像素的Rs。首先令Rs的所有位为0。对于第n(0~10)组来说,对应像素差值用Ω表示,则Ω的取值范围是-255~255。对Ω设置合理的阈值ξ,则Rns的表达式如下:
| $ R_{n}^{s}=\left\{ \begin{align} & 0, \mathit{\Omega }<-\xi \\ & 1, \mathit{\Omega }>\xi \\ & 忽略, \mathit{\Omega }为其他值 \\ \end{align} \right., $ | (1) |
那么
| $ {{R}^{s}}=R_{0}^{s}R_{1}^{s}~\ldots \text{ }R_{10}^{s}. $ | (2) |
即如果第0组“互逆”图像的两幅图像对应像素亮度差值为正且大于ξ,则R0s为1,如果差值为负且小于-ξ,则R0s为0,吻合步骤(1)中的编码规律。对其他组图像做同样处理。R0sR1s … R10s表示0和1的一个排列,最终Rs的值为一个二进制数。
同理可求得
| $ {{R}^{t}}=R_{0}^{t}R_{1}^{t}~\ldots \text{ }R_{9}^{t}, $ | (3) |
则相机坐标系中像素到投影仪坐标系像素对应关系为
| $ R=\left( {{R}^{s}}, {{R}^{t}} \right)=\left( R_{0}^{s}R_{1}^{s}~\ldots \text{ }R_{10}^{s}, \text{ }R_{0}^{t}R_{1}^{t}~\ldots \text{ }R_{9}^{t} \right), $ | (4) |
其中,R为一个二进制坐标。根据第(1)步中的编码规律,遍历相机坐标系的所有像素后,忽略不符合上述关系的像素,只取照片中这台投影仪显示区域的像素。在相机坐标系中该投影仪显示范围内的所有像素均有一个R。如果某一像素(u,v)的R=(Rs,Rt)与投影仪坐标系某一像素二进制坐标值(s,t)相等,则两像素形成对应关系。在本步骤完成后,在照片中该投影仪投影范围内的像素均在投影仪中找到对应的像素,两坐标系中像素坐标值形成对应关系(u, v)->(s, t)。
(4) 投影仪坐标系像素到相机坐标系像素对应关系R-获取
由于投影仪像素与其在照片中所占像素比率有较大差异,比如分辨率为1 280 × 800的投影仪在照片中所占像素的范围可能是600 × 400像素。通过第(3)步照片中600 × 400个像素在投影仪中找到对应的600 × 400个像素。对于投影仪中的这600 × 400个像素也就得到其在相机坐标系中对应的像素,并形成各自的对应关系R-。但是对于投影仪坐标系的其他像素点,在相机坐标系中没有真实存在的像素与其对应,也就是说这些像素的坐标值在相机坐标系中还没有相应的坐标值与其对应。这里采用双线性插值的方法,根据已知的其相邻像素在相机坐标系中对应像素的坐标值进行插值计算,求取这些像素在相机坐标系中对应“虚拟像素”的坐标值,从而获得包含投影仪中全部像素的R-。
(5) 纹理映射
纹理映射是将纹理空间中的纹理像素映射到屏幕空间的像素的过程。已知投影仪空间全部像素和相机空间像素的对应关系后,可以把要输出的图像作为纹理通过OpenGL纹理映射到投影仪空间输出,达到对投影仪的几何校正,使各台投影仪共同输出一幅完整图像。在纹理映射时,关键是指定投影仪像素坐标和对应的纹理坐标,纹理坐标通过投影仪像素在相机坐标系中对应像素的坐标值进行相关计算获得。
2.2 亮度校正原理通过几何校正输出的画面在两台投影仪相邻的地方出现亮度明显高于其他区域的一条亮带[4]。亮带中的图像被重复显示两次,其亮度是其他区域图像亮度的两倍[5],有的区域甚至是多台投影仪共同覆盖,使得图像非常不自然,影响视觉效果。这就需要对其进行亮度校正,消除亮带,使整个画面亮度均匀统一。在这里使用Alpha通道蒙版图像融合的方法对重叠区域亮度进行衰减。
在图像处理中,Alpha用来衡量一个像素或图像的透明度。在非压缩的32位RGB图像中,每个像素是由4部分组成:1个Alpha通道和3个颜色分量(R, G, B)。当Alpha值为0时,该像素是完全透明的,而当Alpha值为255时,则该像素完全不透明[6]。如果针对每台投影仪生成一幅Alpha蒙版图像,该图像每个像素的Alpha值根据相应投影仪像素的位置信息通过相关函数计算获得,使得重叠部分Alpha值相应增大;非重叠部分Alpha为0。在投影输出时将蒙版图像与输出图像融合,达到对重叠区域亮度衰减的效果。
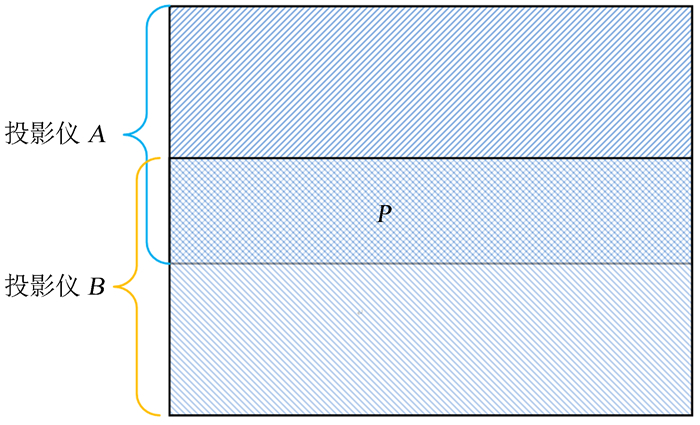
以两个投影仪重合为例介绍Alpha值的计算方法。如图 3,对于重叠区域P之外的所有像素,其Alpha值为0。对于重叠区域之内的像素,为了计算方便,把重叠区域归一化,将两幅图像的重叠部分的坐标归一到0和1之间,0表示重叠区域开始,1表示重叠区域结束。在图 3的上侧投影仪图像可计算Alpha的权重函数如下:
|
| 图 3 两台投影仪重叠示意图 Figure 3 Overlap between two projectors |
| $ F\left( x \right)=\left\{ \begin{align} & 0.5{{\left( 2x \right)}^{p}}, 0\le x\le 0.5 \\ & 1-0.5{{\left[2\left( 1-x \right) \right]}^{p}}, 0.5\le x\le 1 \\ \end{align} \right., $ | (5) |
其中,X为该像素距离重叠区域边缘的距离。p的值用来控制函数F(x)的变化曲线,即蒙版图像中像素亮度的变化规律,从而影响亮度校正的结果。取p=1,用F(x)与255相乘就得到对应像素在蒙版图像中的Alpha值。
2.3 颜色校正原理用于投影拼接的投影仪,颜色空间可能不一致。仔细观察所投影的图像发现,不同投影仪的图像颜色有所差别,影响视觉效果,使得预先对投影仪进行颜色校正十分必要。投影仪的颜色校正主要采用特定方法将不同投影仪颜色空间的差异尽可能减小。
基于硬件技术的颜色校正方法有很多,比如使用色度计的色度匹配技术⑧和用分光辐射计校正的技术⑨。但是这些硬件设备十分昂贵,并且不易实现校正的自动化。文[7]提出了一种针对投影仪颜色模型的非线性最优化方法,参考这种方法结合相机对投影仪进行颜色校正。设投影仪的颜色坐标空间为Mi=[Ri,Gi,Bi]T,i=1, 2 … n,标准颜色的颜色空间为M=[R, G, B]T。设第i个投影仪和标准颜色空间的变换关系为3 × 3的矩阵Hi,
⑧ http://dl.acm.org/citation.cfm?id=769988
⑨ http://ieeexplore.ieee.org/document/885684/
则:
| $ {{M}_{i}}={{H}_{i}}\cdot M, $ |
其中,矩阵Hi为第i个投影仪投影颜色到标准颜色的对应矩阵。
在颜色校正中, 让每个投影仪投影标准颜色模板, 然后定义一个公共的色域作为标准色域。在标准色域内定义标准投影颜色,求取投影颜色到标准颜色的颜色变换函数。假设投影了n个不同颜色方块,投影后就得到n组对应颜色的值,目标是采取相关方法使得
| $ \sum\limits_{i}^{n}{\|{{M}_{i}}-H{{M}_{pi}}{{\|}^{2}}} $ | (6) |
的值最小。通过非线性最优化方法[7]求得满足条件的H,则H-就是颜色校正中所需要的变换矩阵。
3 球幕投影拼接校正系统实现 3.1 系统开发运行环境系统基于Ubuntu开发,以C++为编程语言。纹理映射部分调用OpenGL相关库函数。
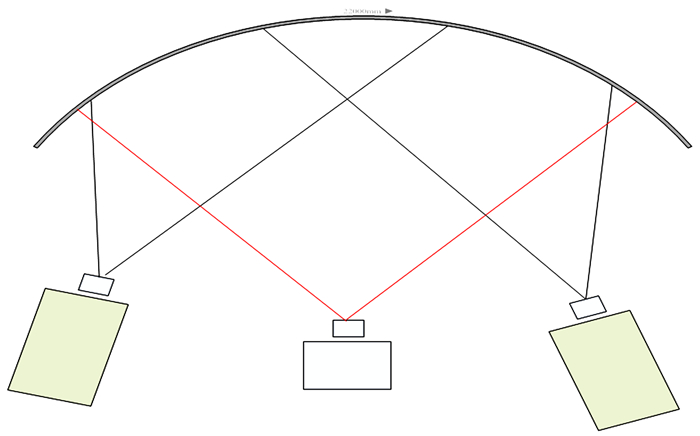
3.2 投影仪、相机配置首先选择合适的数码相机和鱼眼镜头,相机选用目前主流分辨率数码相机。根据球幕尺寸大小,合理搭配数码相机和镜头,调节相机高度和焦距使其视野覆盖球幕并且拍摄画面比较清晰。把主控计算机和显示分机连接网络,获得各台计算机的IP。相机与主控机连接,各分机与投影仪连接。投影仪固定在球幕边缘,调节投影仪位置使各投影仪在球幕上的投射区域有部分重叠,如图 4。在校正过程进行之前,要遮蔽室内的可见光源,以免影响相机的拍照质量。因为相机拍照质量的好坏直接影响几何校正过程中坐标系对应关系R的求取。在校正过程中确保相机、投影仪位置固定不变。
|
| 图 4 相机投影仪配置图 Figure 4 Deployment diagram of the camera and two projectors |
(1) 对主控机进行参数设置:投影仪数目、投影分辨率、各分机的IP地址等。这里以两台投影仪为例。
(2) 依次对每台投影仪进行编码图像显示,主控机驱动相机拍照,去噪后存储。
(3) 设置合理阈值,求取R、R-。
(4) 对输出图像预校正,向球幕输出校正后的图像。此时可以在球幕上得到无缝拼接的图像,如图 5(b),可以看到两投影仪重叠区域有明显亮带。
|
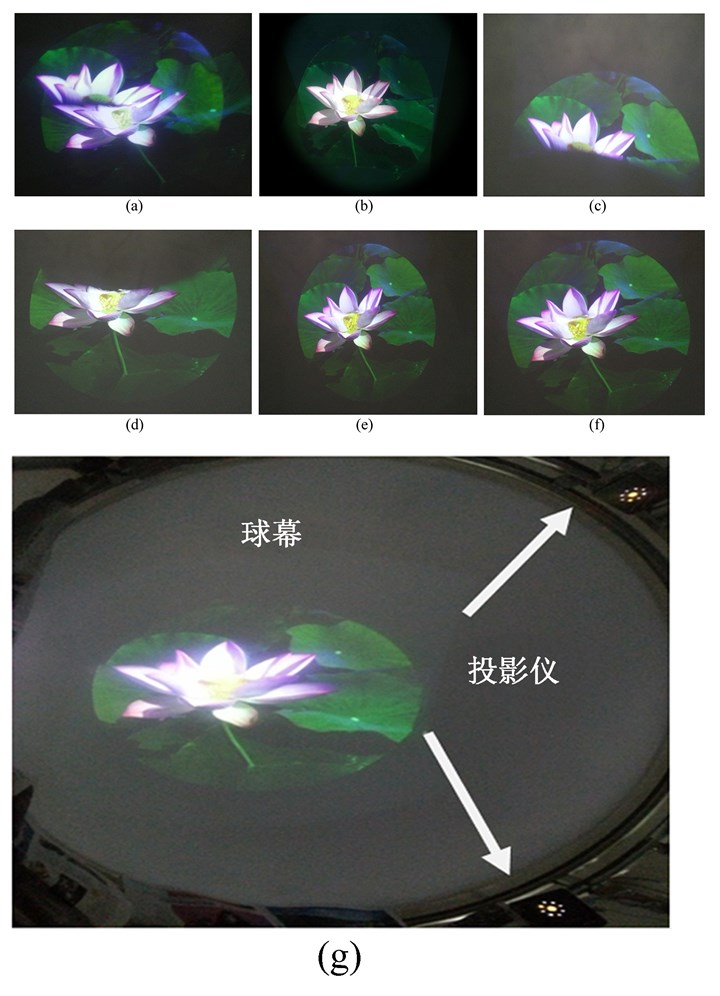
| 图 5 (a)几何校正前输出图像;(b)几何校正后输出图像;(c)、(d)两台投影仪各自输出的图像;(e)亮度校正后输出图像;(f)颜色校正后图像;(g)实验时的球幕和投影仪 Figure 5 (a) The output image before geometric correction; (b) The output image after geometric correction; (c) and (d) are images output by two projectors respectively; (e) The output image after brightness correction; (f) The output image after color correction; (g) The dome and projectors in experiment |
根据在几何校正过程中得到的投影仪位置关系,可得到投影仪之间的重叠区域。把重叠区域归一化,根据(5)式分别计算各台投影仪的蒙版图像。所有蒙版图像计算完毕与相应投影仪图像融合后输出,进而对重叠区域进行亮度衰减,使得球幕上的整个画面亮度均匀统一。
3.5 颜色校正(1) 首先用常用颜色制作颜色棋盘,比如8位图像的256色,用各投影仪将颜色棋盘投影,并用相机拍照。
(2) 根据几何校正中求得的坐标系对应关系,可以获得对应颜色方块的颜色,得到同一颜色方块经过不同投影仪投影后的不同颜色值。
(3) 根据非线性最优化方法求得各个投影仪的颜色校正对应性矩阵H-。颜色校正在各投影仪进行图像显示时实时执行,H-应用在各图像被分开显示到投影仪的瞬间。
图 5(a)为几何校正前两投影仪的输出结果,这种现象通过几何校正在图 5(b)中得到纠正。比较图 5中(b)和(e),可以看出图 5(b)中两投影仪的亮带在图 5(e)中得以消除。这里需要说明, 目前市场主流投影仪颜色差别不大,投影仪间的颜色空间基本一致,加之对显示后的图像进行拍照,然后放在本文中,所以在颜色校正前后的输出图像图 5的(e)和(f)之间的差别不是很明显。
球幕投影校正的各个步骤执行完毕后,加载图像或视频,通过各台投影仪的输出最终可以在球幕上得到无缝拼接、颜色亮度均匀统一的画面。为了保证各台投影仪输出画面的实时同步性,建议在硬件上各台主机和投影仪要尽量采用同一设备型号。在视频播放软件上,对各通道投影仪要保证视频各帧的同步输出。
4 总结与展望本文提出了针对中小型球幕天象厅的多投影自动拼接技术的设计和具体实现方法。尝试解决该技术中的几何校正、重叠区域的亮度校正、投影仪之间的颜色校正等关键问题。实验证明,该方法在构建面向球幕的多投影显示系统中具有可行性并收到较好的效果。系统配置方便,操作简单,未来将整合到万维天文望远镜互动式数字天象厅系统中,促进中国天文科普教育事业的发展。
致谢:
感谢中国虚拟天文台(China-VO)研发团队、国家天文台信息与计算中心、重庆悟台科技发展有限公司对相关实验的指导和本文完成提供的大力支持。
| [1] |
袁慧明. 天象厅中的数字革命[J]. 现代电影技术
, 2011 (3) : 26 –30 |
| [2] |
曹双喜, 陈福民. 多投影仪拼接显示的实现[J]. 计算机工程与应用
, 2005 , 10 (2) : 84 –86 Cao Shuangxi, Chen Fumin. Implementation of multi-projector displays[J]. Computer Engineering and Applications , 2005 , 10 (2) : 84 –86. |
| [3] | Raskar R, Baar J V, Chai J X. Alow-cost projector mosaic with fast registration[C]//In Proceedings of Fifth Asian Conferenceon Computer Vision. 2002. |
| [4] |
倪政国, 陈蕾. 视景光学显示技术[M].
吉林: 吉林科学技术出版社. 2003.
|
| [5] |
汤顺清. 色度学[M].
北京: 北京理工大学出版社. 1990.
|
| [6] |
黄三发, 陈福民, 陈小灿. ALPHA融合在无缝投影中的应用[J]. 计算机应用与软件
, 2007 , 24 (12) : 161 –162+186 Huang Sanfa, Chen Fumim, Chen Xiaochan. The application of ALPHA blending to seamless projection[J]. Computer Applications and Software , 2007 , 24 (12) : 161 –162+186. |
| [7] | 李斌.低成本多投影仪拼接方法研究[D].济南:山东大学, 2005. |



