2. 中国科学院大学, 北京 100049;
3. 中国科学院射电天文重点实验室, 江苏 南京 210008
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, China
基于中央处理器的多相滤波器组设计,由于算法本身的复杂度和计算量,导致仿真消耗时间长且执行效率低。借助图形处理器高效的并行执行能力与通用并行计算架构(Compute Unified Device Architecture, CUDA)[1]的高性能并行架构,能够有效地改善多相滤波器组算法在高速数据处理方面效率低下的问题。
通用并行计算架构是一种由NVIDIA公司开发的并行编程模型,可加速图形处理器的高速并行处理、高效解决海量且逻辑简单的计算问题,包含指令集架构以及图形处理器内部的并行计算引擎[2]。图形处理器计算能力的迅速发展已超过摩尔定律①,目前主流图形处理器的单精度浮点处理能力和外部存储器带宽相对于中央处理器有明显的优势,通用并行计算架构在编程、优化等方面都得到了显著的提升,大大增强了图形处理器的通用计算能力。
① http://docs.nvidia.com/cuda/cuda-c-programming-guide/#axzz4NhrMoSok
随着并行处理技术的发展,图形处理器已成了实时处理天文信号的首选。射电望远镜数字终端[3]通过多相滤波器进行分通道、滤波并有效控制快速傅里叶变换产生的频谱泄露,多相滤波器是数字滤波器组的一种高效实现形式[4]。近年来,多相滤波技术在射电望远镜终端设备开发中得到了广泛应用,例如脉冲星终端、消色散系统、相关器及数字频谱仪等。图形处理器和通用并行计算架构技术为多通道射电天文多相滤波器组设计提供了一种高速实现的途径。
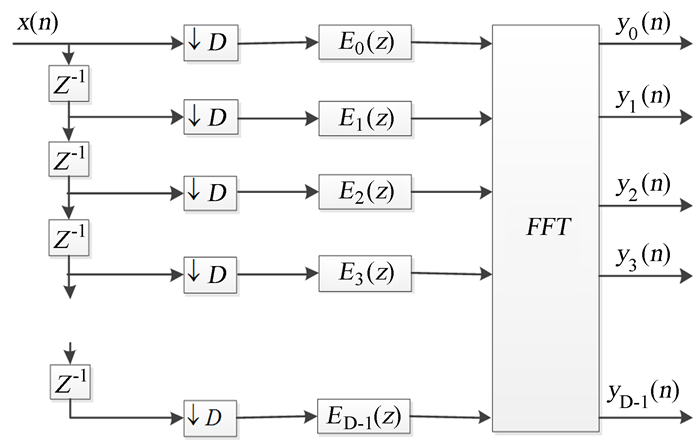
1 多相滤波器组原理射电天文多相滤波器组主要由多个分解的有限长单位冲激响应(Finite Impulse Response, FIR)滤波器和快速傅里叶变换组成,处理过程包含频谱转移、抽取、滤波、快速傅里叶变换等。分解的有限长单位冲激响应滤波器跟其他数字滤波器相比有许多优点,性能稳定,可实现严格的线性相位和任意幅度[5]。多相滤波器组的基本原理如图 1。
|
| 图 1 多相滤波器组结构图 Figure 1 Structure chart of the Polyphase filter bank |
滤波器组中的多相分解将数字滤波器的冲击响应函数分解为多个不同的相位进行处理,将复杂多阶的滤波器简化为多个低阶的滤波器,提高运算速率。
有限长单位冲激响应滤波器的转移函数表达式为
| $ \begin{align} & H\left( z \right)=\sum\limits_{n=0}^{N-1}{h\left( h \right){{z}^{-n}}} \\ & =h\left( 0 \right)+h\left( 1 \right){{z}^{-1}}+\ldots +h\left( N-1 \right){{z}^{N-1}}, \\ \end{align} $ | (1) |
其中,N为滤波器长度。将H(z)分解成D组,设N/D=Q,且Q取整数,可以得到:
| $ \begin{align} & H\left( z \right)=h\left( 0 \right){{z}^{0}}+h\left( D \right){{z}^{-D}}+\cdots +h\left[ \left( Q-1 \right)D \right]{{z}^{-\left( Q-1 \right)D}} \\ & =\sum\limits_{n=0}^{Q-1}{h\left( nD+0 \right){{\left( {{z}^{D}} \right)}^{-n}}+{{z}^{-1}}}\sum\limits_{n=0}^{Q-1}{h\left( nD+1 \right){{\left( {{z}^{D}} \right)}^{-n}}+\cdots } \\ & +{{z}^{-(D-1)}}\sum\limits_{n=0}^{Q-1}{h\left( nD+D-11 \right){{\left( {{z}^{D}} \right)}^{-n}},} \\ \end{align} $ | (2) |
令
| $ H\left( z \right)=\sum\limits_{k=0}^{D-1}{{{E}_{k}}({{z}^{D}})\cdot {{z}^{-k}}}, $ | (3) |
其中,Ek(zD)表示H(z)的多相分量。
采用离散傅里叶变换(Discrete Fourier Trans-form, DFT)对分解的有限长单位冲激响应滤波进行变换,获得输入信号的频谱响应。输入信号x(n)的离散傅里叶变换如(4)式,产生频谱系数X(k),其中k∈ [0, N-1]。原来的信号x(n)也可以通过频谱系数合成获取,如(5)式。
| $ X\left[k \right]=\sum\limits_{n=0}^{N-1}{x\left[n \right]{{e}^{-j\left( 2\pi /N \right)kn}}}, $ | (4) |
| $ x\left[n \right]=\frac{1}{N}\sum\limits_{n=0}^{N-1}{X\left[k \right]{{e}^{j\left( 2\pi /N \right)kn}}.} $ | (5) |
对信号进行快速傅里叶变换处理时,输入信号的时域和频域都是离散的,并且都是有限长。因此必须对实际模拟信号进行采样并在时间上截取一定片段[6],然后用离散傅里叶变换算法对信号进行分析。实际信号处理时,快速傅里叶变换作周期性延拓,因为数字终端处理的数据是有限时间段内,而快速傅里叶变换要求时间从负无穷到正无穷的积分。
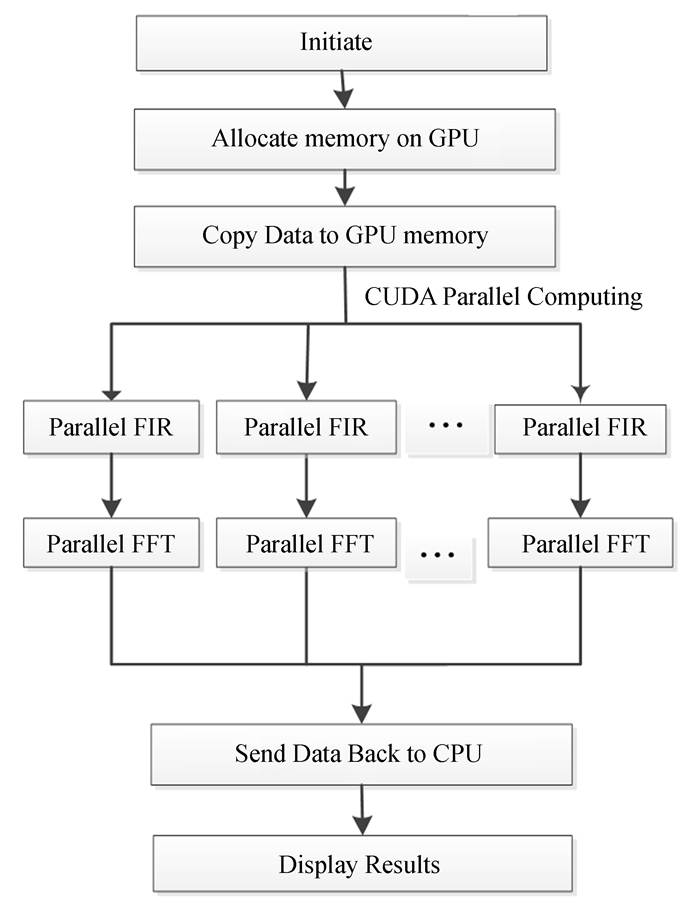
2 多相滤波器组设计与性能测试基于通用并行计算架构的射电天文多相滤波器组设计流程如图 2。中央处理器和图形处理器协调完成多相滤波,中央处理器负责逻辑控制和串行相关的工作,图形处理器则负责高度并行的数据处理任务。首先中央处理器完成初始化、准备待处理的数据,cudaMalloc ()创建图形处理器的内存空间,cudaMemcpy ()函数把数据从中央处理器复制到图形处理器显存,然后启动CUDA kernel对算法进行并行处理。为了加速算法,提前生成基于窗口函数的多相滤波器组系数,然后将系数传输到图形处理器共享内存,把数据跟多相滤波系数相乘实现有限长单位冲激响应滤波,再进行快速傅里叶变换,最后将数据从图形处理器显存复制到中央处理器内存,显示处理结果。快速傅里叶变换使用通用并行计算架构的cuFFTlibrary②,cuFFT能够快速实现离散傅里叶变换。在设计中使用cuFFT的cufftExecC2C ()函数并行高速实现快速傅里叶变换算法。
② http://docs.nvidia.com/cuda/cufft/#axzz4NhrMoSok
|
| 图 2 基于通用并行计算架构的多相滤波器组的实现流程图 Figure 2 Flow chart of the polyphase filter bank implementation based on CUDA |
cuFFT是通用并行计算架构快速傅里叶变换库,可大幅提高快速傅里叶变换的速度,速度最高提升10倍。cuFFT提供一个简单的编程接口,能够对复数与实数一维、二维和三维变换,一维变换最大为1.28亿个元素,可以单精度和双精度变换,数据布局灵活。
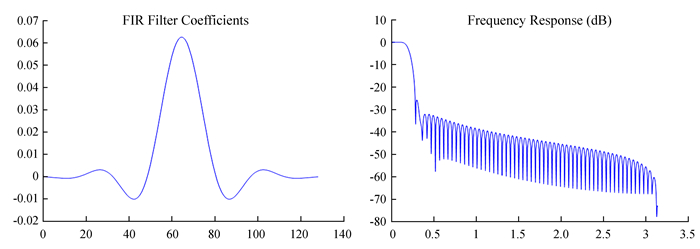
设计中为了减少快速傅里叶变换处理过程的频谱泄漏,添加窗口函数对信号进行处理,图 3是汉明(Hamming)窗口的有限长单位冲激响应滤波器脉冲响应及频率响应。
|
| 图 3 汉明窗口的有限长单位冲激响应滤波器 Figure 3 FIR filter based on hamming window |
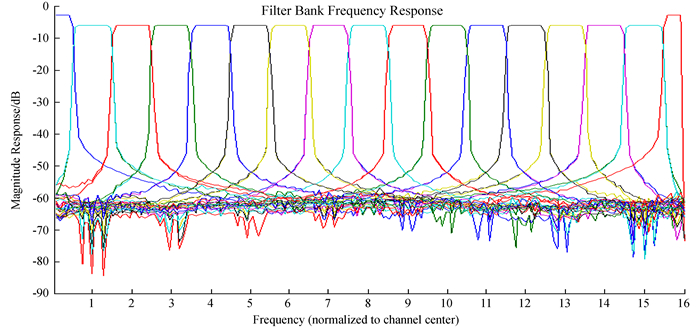
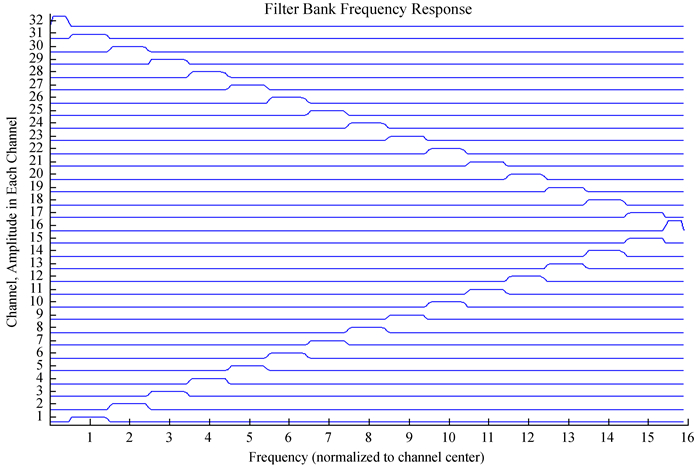
多相滤波器组和普通的快速傅里叶变换相比可以更有效地进行通道化,消除频谱泄露。对8-Tap、32通道多相滤波器的仿真结果如图 4、图 5。多相滤波器组通道N/2点对称,32通道的多相滤波器,32/2=16点对称。
|
| 图 4 多相滤波器组频谱响应 Figure 4 Frequency response of the polyphase filter bank |
|
| 图 5 多相滤波器组通道 Figure 5 Polyphase filter bank channels |
射电天文多相滤波器组的设计、实验和测试环境如表 1,测试中所用的软件和硬件环境包括Ubuntu 14.04操作系统,Nsight Eclipse, IntelXeonE5中央处理器,NVIDIA Quadro K620图形处理器,8 GB内存等。
| Name | Parameter |
| Device | Quadro K620 |
| CUDA Driver Version/Runtime Version | 7.5/7.5 |
| Total amount of global memory | 2 047 Mbytes (2 146 762 752 bytes) |
| CUDA Cores | 384 CUDA Cores |
| Memory Bus Width | 128-bit |
| Warp size | 32 |
| Maximum number of threads per block | 1 024 |
| Max dimension size of a thread block (x, y, z) | (1 024, 1 024, 64) |
| Max dimension size of a grid size (x, y, z) | (2 147 483 647, 65 535, 65 535) |
| Total amount of shared memory per block | 49 152 bytes |
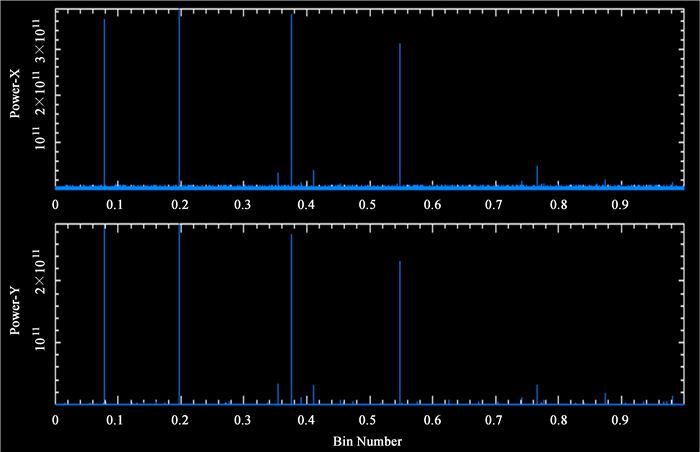
为了验证基于通用并行计算架构的射电天文多相滤波器组性能,针对不同通道的多相滤波器组的输出、吞吐量及数据处理消耗时间进行了测试和分析。首先生成32 MB、采样频率128 MHz、8 bit双极化的加噪声复数信号,然后将数据从内存传输到图形处理器中,使用多相滤波器组进行处理。运算中将8 bit数据转换为单精度浮点数,每组数据进行多相滤波器及快速傅里叶变换运算,最后将输出数据求平方根,得出能量谱,并从图形处理器传输到内存,显示处理结果。实验中tap=8,使用6 144个图形处理器物理线程,实验结果如图 6、图 7。

|
| 图 6 1 024通道多相滤波器组输出 Figure 6 Output of the polyphase filter bank with 1 024 channels |
|
| 图 7 1 048 576通道多相滤波器组输出 Figure 7 Output of the polyphase filter bank with 1 048 576 channels |
图 6、图 7是多相滤波器组通道数1 K和1 024 K的频谱输出,当Channel=1 K时,由于噪声干扰的影响,输出的能量谱不是很理想,但是随着通道数的增加,多相滤波器组的输出分辨率提高,信号检测能力增强。
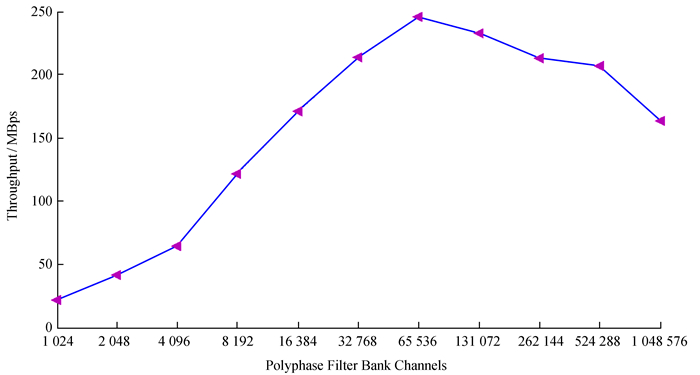
图 8是多相滤波器组通道数及吞吐量之间的变化曲线。多相滤波器组的吞吐量随通道数的增加而提高,当通道数量为65 536时,吞吐量最高,然后开始下降趋势。
|
| 图 8 多相滤波器组通道数和吞吐量的关系 Figure 8 Throughput capacity variations as a function of channel number |
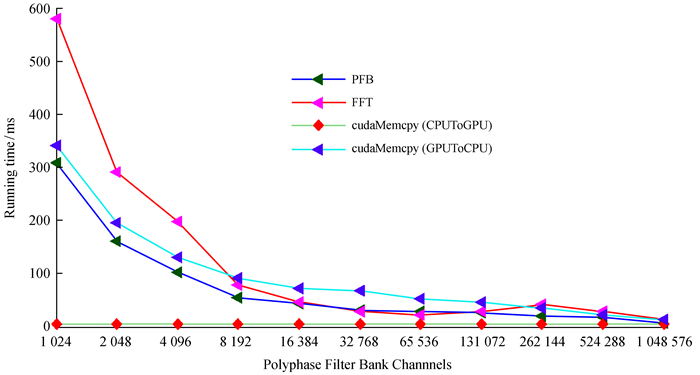
如图 9,算法在数据传输、多相滤波器及快速傅里叶变换运算处理三方面时间消耗较大。而随着通道数的增加,多相滤波器组的平均数据处理时间趋势减少。1 K通道多相滤波器及快速傅里叶变换占用的时间约为308 ms、580 ms,当Channel=1 024 K时,它们的数据处理时间分别为是7 ms、13 ms。
|
| 图 9 多相滤波器组通道数和数据处理消耗时间 Figure 9 Data processing time variations as a function of channel number |
多相滤波器组的数据处理主要消耗时间体现在快速傅里叶变换、多相滤波器的运算和将数据从图形处理器显存传输到中央处理器内存的过程中。当通道数为1 K~16 K时,数据处理时间减少趋势明显,然后减少趋势放缓。实验及测试结果表明,通用并行计算架构能够高速实现多通道射电天文多相滤波器组。通过通用并行计算架构技术可加速算法,提高百万通道数的并行处理速度,该设计能够很好地满足数字终端对信号的信道化与快速处理的需求。
3 结论基于通用并行计算架构实现的射电天文多相滤波器组,充分利用图形处理器的多线程、多核并行执行能力,大幅提升了滤波器组实时处理性能。针对计算量较大的滤波、快速傅里叶变换算法应用通用并行计算架构编程实现了算法的并行化,并对其吞吐量、数据处理消耗时间及不同通道输出的功率谱进行测试及相关的优化。设计的多相滤波器组易于扩展和升级,采用通用并行计算架构加速多相滤波,提高了算法的计算效率。
| [1] | Nickolls J, Buck I, Garland M, et al. Scalable parallel programming with CUDA[J]. Queue , 2008 , 6 (2) : 40 –53. DOI: 10.1145/1365490 |
| [2] | Ryoo S, Rodrigues C I, Baghsorkhi SS, et al. Optimization principles and application performance evaluation of a multithreaded GPU using CUDA[C]//Proceedings of the 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. 2008:73-82. http://www.oalib.com/references/19319074 |
| [3] |
赵欣, 金乘进, 朱岩, 等. 基于多相滤波的多通道数字终端设计[J]. 天文研究与技术
, 2015 , 12 (4) : 495 –502 Zhao Xin, Jin Chengjin, Zhu Yan, et al. A design of a multi-channel digital backendbased on a polyphase filter bank[J]. Astronomical Research & Technology , 2015 , 12 (4) : 495 –502. |
| [4] |
朱凯, 甘恒谦, 朱岩, 等. 多相滤波器组谱分析方法的性能讨论与天文观测应用[J]. 天文研究与技术—国家天文台台刊
, 2011 , 8 (1) : 81 –90 Zhu Kai, Gan Hengqian, Zhu Yan, et al. On the performance of spectral analysis with a polyphase filter bank and its applicationin radio astronomy[J]. Astronomical Research & Technology—Publications of National Astronomical Observatories of China , 2011 , 8 (1) : 81 –90. |
| [5] |
陈宇燕, 郭平. Matlab辅助DSP实现FIR数字滤波器[J]. 轻工科技
, 2013 , 12 : 57 –58 Chen Yuyan, Guo Ping. Matlab aid DSP in approaching FIR digital filter[J]. Light Industry Science and Technology , 2013 , 12 : 57 –58. |
| [6] |
赵仁才, 颜龙, 郭军. 短波信号实时频谱分析仪设计[J]. 电子测量技术
, 2004 , 4 : 9 –10 Zhao Rencai, Yan Long, Guo Jun. The design of real-time frequency spectrum analyzer for HF signal[J]. Electronic Measurement Technology , 2004 , 4 : 9 –10. |



