2. 中国科学院天文光学技术重点实验室, 江苏 南京 210042;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Astronomical Optics & Technology, Nanjing Institute of Astronomical Optics & Technology, Chinese Academy of Sciences, Nanjing 210042, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
无论是美国国家点火装置(National Ignition Facility, NIF),我国的激光惯性约束核聚变(Inertial Confinement Fusion, ICF),还是大天区面积多目标光纤光谱天文望远镜(Large Sky Area Multi-Object Fiber Spectroscopy Telescope, LAMOST),也叫郭守敬望远镜都大量使用大口径平面元件。郭守敬望远镜的施密特反射镜由24块对角线1.1 m的六角形反射镜拼接而成,国家点火装置高功率激光系统则计划使用500余件大口径平面元件。总之,大口径平面光学元件作为天文、航空航天、激光核聚变等大型光学系统的核心元件,得到了越来越广泛的应用。这些大口径平面元件的面形质量与它们所参与的光学系统的成像质量直接相关,因此,如何高精度检测大口径平面面形是目前大口径平面元件使用的一个瓶颈[1]。
测量精度决定了加工精度。光干涉测试技术是公认的检验光学元件最精密的方法之一,它是以波长为计量单位的高精度测量方法。而干涉仪则是利用干涉技术进行测量的仪器,随之发展的移相干涉技术大大提高了干涉仪在光学测量上的应用[2]。然而,在平面的高精度检测中,Fizaeu干涉仪测量的光学平面的面形是测试面和参考面共同相对于理想平面的偏差。传统的方法使用更高精度的平面作为干涉仪的参考面。所以,对于平面的高精度测量受限于干涉仪参考面的面形精度,则需要研究新方法检测干涉仪参考面的绝对面形,从检测平面面形的结果中消除参考面的面形误差,才能实现平面光学元件的高精度测量。
1 绝对检验简介国内外对于平面元件的绝对检验有很多经典的方法,但对于大口径平面元件检测也各有弊端。
文[2]提出的液面法,精度高,但是易受振动、温度等外界干扰;文[3]提出的三面互检法,只能检测沿直径方向直线上的轮廓;文[4]提出的利用泽尼克(Zernike)多项式拟合方法,大口径平面在大多情况下,只存在较低频误差,合适用一组多项式拟合,但需要旋转和多次更换干涉仪标准平晶,易引入误差,对于大口径平面检测风险大;文[5]的奇偶函数法和文[6]的旋转剪切法,都是在传统双面互检法的基础上提出的,但都需要反复旋转和更换平晶,检测风险大,不利于大口径平面元件的测量。
本文采用双平晶互检法检测干涉仪参考面的绝对面形,对比于上述大口径平面的标定方法,双平晶互检法不需要反复更换干涉仪参考面,降低了风险,节约了测试时间,可操作性强。本文旨在利用MATLAB对双平面互检法进行数理上的验证,并进行误差分析,用于标定大口径干涉参考平晶提供理论支持。
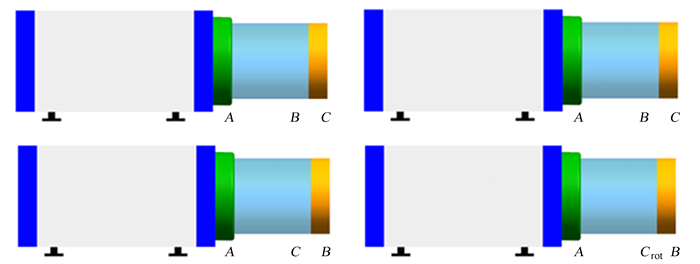
2 双平晶互检法原理文[7]介绍了双平晶互检法的原理,平晶Ⅰ放置于平面干涉仪标准参考平晶的位置,平晶Ⅱ放置于待测面的位置。4次测量步骤如图 1。
|
| 图 1 4次测量的示意图 Figure 1 Schematics of these four measurements |
(1) 平晶Ⅰ的后表面A与平晶Ⅱ的前表面B干涉;
(2) 平面A与平晶Ⅱ的后表面C干涉;
(3) 将平晶Ⅱ沿x轴翻转180°后,平面A与平面C干涉;
(4) 将平晶Ⅱ再绕z轴逆时针旋转φ角,平面A与平面C干涉。
M1(x, y)、M2(x, y)、M3(x, y)、M4(x, y)为干涉仪4次测得的波面信息,根据任何一个二维函数都可以分解成旋转不变量、旋转因变量和泽尼克多项式形式上的旋转不变性,并消除了调整误差,即可得到平面A的绝对面形。
3 双平晶互检法测量的仿真本文不仅从数据(即均方根(Root Mean Square, RMS)值和峰谷值)上给出了泽尼克多项式项数和可能存在的误差对结果的影响,而且用面形相减和图形更直观地反应误差导致的面形变化,对于实际设计加工更具有指导作用。
首先,对双平晶互检法的实验过程、原理进行模拟仿真,分析模拟的结果,并对双平晶互检法原理中泽尼克拟合采用的多项式项数进行仿真分析;其次,对双平晶互检法实验过程中可能存在的对准误差进行仿真分析,主要包括旋转对准误差和平移对准误差。
3.1 双平晶互检法 3.1.1 双平晶互检法的原理仿真在双平晶互检法的4次测量中,已知条件是4次干涉仪得到的测量结果M1、M2、M3、M4,所求解的是A、B、C 3面的面形误差。本文仿真的主要思路为:利用给出的A、B、C 3面的面形矩阵,求得4次测量的干涉结果M1、M2、M3、M4;然后根据双平晶互检法的原理,利用M1、M2、M3、M4计算A、B、C 3面的面形;最后将得到的面形和给出的面形进行比较分析。本文利用这样的闭环分析思路,借助MATLAB强大的数据分析能力,可以有效地验证双平晶互检法。
仿真按照以上思路进行,主要分为以下几步:
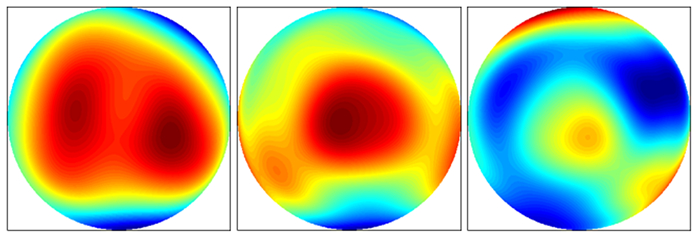
(1)随机给出A、B、C3面的面形矩阵,其面形误差控制在干涉仪能检测范围内,图 2中数据是利用ESDI公司的菲索干涉仪在一次平面检测中得到的平面面形数据,分别求出4次干涉结果M1、M2、M3、M4。
|
| 图 2 给出的A、B、C3面的面形图像 Figure 2 Surface images of three given faces: face A, B and C |
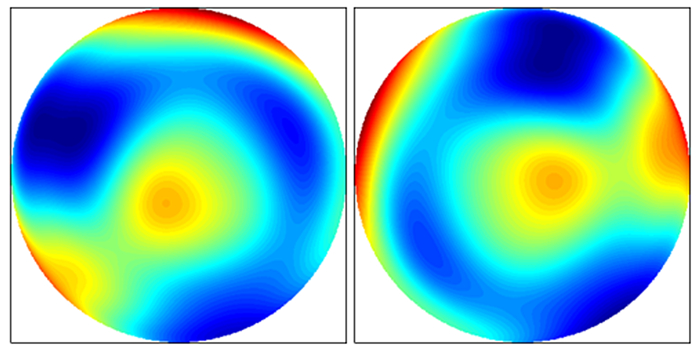
4次测量方程中,涉及到了C面的翻转和旋转问题。对比到矩阵上,C面的翻转就是对矩阵翻转和正负取反,C面的旋转就是矩阵的旋转,本文这里旋转角度采用-54°[7]。图 3为C面矩阵翻转和旋转对应的面形图像,测量方程中的折射率采用n=1.5,并且假设非均匀性误差处于理想状态δ(x, y)=0。
|
| 图 3 C面的翻转和旋转的面形图像 Figure 3 Surface images with face C turned and rotated |
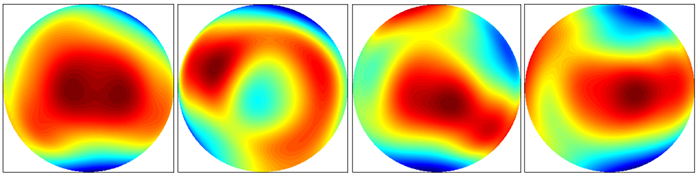
综上所述,4次测量中各个参数A(-x, y)、B(x, y)、C(-x, y)、C(x, y)、Cφ(x, y)的矩阵数据都已经得到。所以,按照4次测量方程即可以求得4次干涉结果M1、M2、M3、M4的面形矩阵,图 4为4次干涉的面形图像。
|
| 图 4 干涉结果M1、M2、M3、M4的面形图像 Figure 4 Surface images of M1, M2, M3 and M4 with interference |
(2) 将上一步得到M1、M2、M3、M4干涉结果矩阵作为已知条件,利用双平晶互检法的算法原理,求出A、B、C3面的面形误差矩阵。
根据双平晶互检法的原理可知,计算A、B、C3面面形分为两步,分别计算A、B、C面形误差的旋转不变量和旋转因变量两部分。首先,将已知条件M1、M2、M3、M4分别利用最小二乘法进行泽尼克36项拟合,分别得到其泽尼克36项系数[8]。其次,泽尼克36项可分为旋转不变项和旋转因变项,泽尼克36项系数中第1、4、9、16、25、36项系数为旋转不变项,其余为旋转因变项[9]。最后,分别利用泽尼克36项中旋转不变项和旋转因变项进行计算,得出A、B、C3面的面形矩阵。
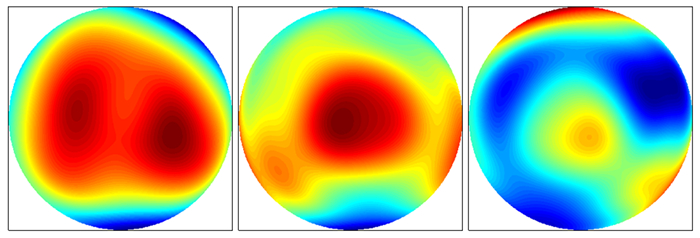
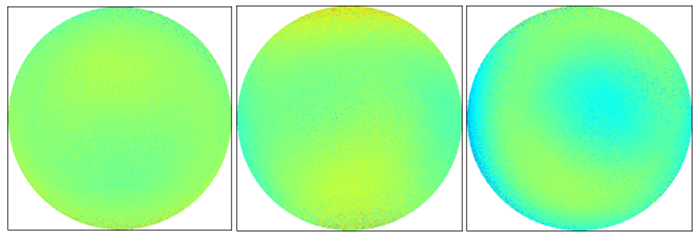
3.1.2 双平晶互检法计算结果分析首先,比较A、B、C原给出的面形和双平晶互检法计算拟合得出的面形。图 2分别是原给出的A、B、C3个面形,而图 5则是按照三面互检原理计算得到的面形,可以看出3个面的高低分布趋势一样。将拟合的A、B、C面形矩阵与原给出的面形矩阵相减,如图 6,可以直观看出拟合的精度。由两面形相减所得到的矩阵图像可以看出,颜色变化不明显,即两面形矩阵每个位置对应的高低模拟得非常吻合。
|
| 图 5 双平晶互检法计算得出A、B、C的面形图像 Figure 5 Surface image of A, B and C computed by the Two Flats Test |
|
| 图 6 双平晶互检法计算得出A、B、C的面形图像与原面形相减图像 Figure 6 Images after subtracting surface images computed by the Two Flats Test from those original surface |
另外,通过分别计算两面相减得到的矩阵元素的均方根值定量给出双平晶互检法的拟合程度如表 1。
| A面 | B面 | C面 | |
| 均方根值(RMS) | 2.0418e-34 | 4.6895e-34 | 1.0995e-33 |
表中的3个值均是在不考虑其他测量误差的情况下理论模拟值,其值均极小,对于工程应用完全可以忽略不计。由表 1中数据可以得出这种拟合误差的大小在10-33量级,这是由于在双平晶互检法中,C面的旋转在计算中引入了三角函数,软件的默认计算精度是32位,即一个三角函数的值是用了一个32位小数代替导致的误差,此误差并非原理带来的误差,也就验证了双平晶互检法的正确性。
其次,分析计算过程中泽尼克多项式的项数对结果的影响。仿真过程中采用目前大多数干涉仪使用的泽尼克多项式的前36项进行拟合分析。对应于接收器上采样点的数目,泽尼克多项式项数的选取有一个最优的范围。仿真过程中面形矩阵的大小为1 024 × 1 024,当泽尼克拟合项数过少,使得不能充分利用采样点数,丢失了高频信息;当泽尼克拟合项数过多,使得运算周期变长,而拟合效果很难再得到提升。
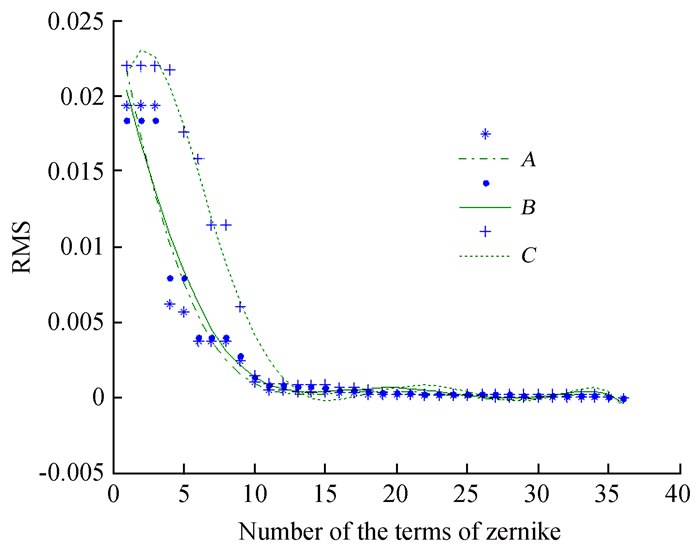
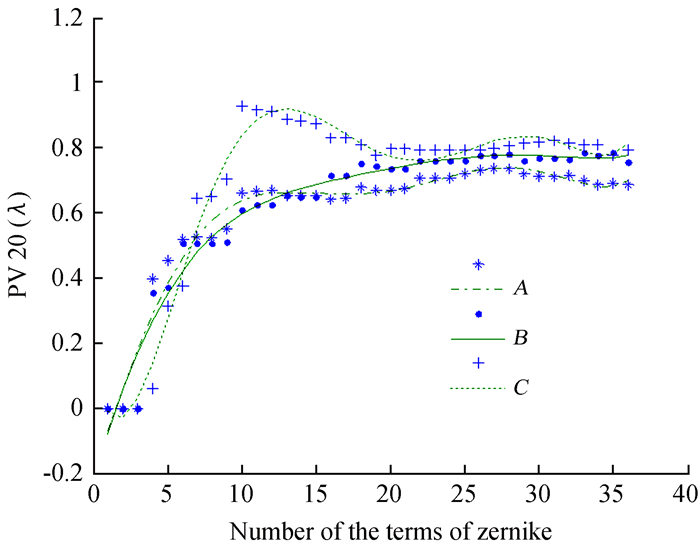
分别利用泽尼克第1项到第36项进行双平晶互检法的仿真,通过拟合面形相对于原面形的均方根值和拟合面形的峰谷值来分析泽尼克多项式项数的影响,如图 7、图 8。图 7中,星点表示不同泽尼克多项式项数拟合得到的面形与原面形之间的均方根值,曲线表示对这些点值进行拟合。从中可以得出当采用的泽尼克多项式项数大于15时,拟合的A、B、C3面形相对于原面形的均方根值变化均趋于稳定,稳定于0附近;图 8中,星点表示不同泽尼克多项式项数拟合得到面形的峰谷值,曲线表示对这些点值进行拟合。从中可以得出,曲线从第35、36项开始趋于稳定。综合均方根值和峰谷值的考虑,在实验仿真中采用泽尼克前36项。
|
| 图 7 均方根值随泽尼克多项式项数的变化 Figure 7 RMS variations as a function of the number of Zernike terms |
|
| 图 8 PV20值随泽尼克多项式项数的变化 Figure 8 PV20 variations as a function of the number of Zernike terms |
表 2给出了分别利用泽尼克前6、12、18、24、30、34、36项拟合,计算得到的各个面对应的均方根值和峰谷值。从表中数据和图 7、图 8可以看出,随着泽尼克多项式项数的增加,均方根值呈减小的趋势,即拟合程度在提高;随着泽尼克多项式项数的增加,峰谷值呈增大的趋势,即拟合的面形中更好地体现了高频信息。
| 6 items | 12 items | 18 items | 24 items | 30 items | 34 items | 36 items | |||||||||||||||
| RMS | PV | RMS | PV | RMS | PV | RMS | PV | RMS | PV | RMS | PV | RMS | PV | ||||||||
| A | 0.003 7 | 0.518 7 | 0.479 9 | 0.671 8 | 0.188 1 | 0.676 9 | 0.125 4 | 0.705 6 | 0.383 8 | 0.712 5 | 0.434 9 | 0.687 5 | 0.000 0 | 0.686 2 | |||||||
| B | 0.004 0 | 0.506 2 | 0.809 2 | 0.623 3 | 0.352 9 | 0.750 8 | 0.241 2 | 0.760 8 | 0.166 6 | 0.767 9 | 0.135 8 | 0.778 2 | 0.000 0 | 0.755 1 | |||||||
| C | 0.015 8 | 0.376 7 | 0.949 0 | 0.912 7 | 0.492 4 | 0.809 9 | 0.242 4 | 0.792 7 | 0.186 1 | 0.819 1 | 0.176 7 | 0.807 1 | 0.000 0 | 0.792 6 | |||||||
为了让仿真更接近于实验过程,接下来模拟仿真实验过程中的主要误差来源。采取控制变量法,逐一分析各误差对实验结果的影响。双平晶互检法优点在于只对一个平晶进行翻转和旋转操作,相对于传统三面互检法更容易控制误差的引入。
本文4次测试装调中,理想状态是两个面完全对准。当然,实验过程中不可能达到这样的理想状态。在4次测试装调中,既要保证两个面在平移方向上对准,要保证每次测试中两个面关于中心旋转方向上对准。下文就这两种误差来源分别进行仿真分析[10]。
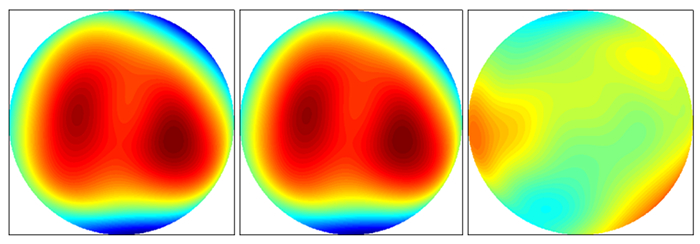
3.2.1 旋转对准误差分析由双平晶互检原理和仿真过程可以知道,求解A、B、C3面的面形矩阵过程中,先求出C面的面形,然后依据C面形,求出A、B面的面形。因此,计算的C面形中含有的误差直接传递给A、B面形,误差大小一致。因为这里忽略其余误差,只分析单个旋转角度引入的误差,所以只利用干涉仪参考平晶I面形分析误差。MATLAB仿真过程采用的旋转角度是-54°,这里分析角度误差在±2°,采样点40。图 9显示A的理论面形和旋转角度偏差+2°的面形,以及两个面的面形误差。
|
| 图 9 A面形、含误差的A面形、两面形误差图 Figure 9 Face A, face A with error and the error graph |
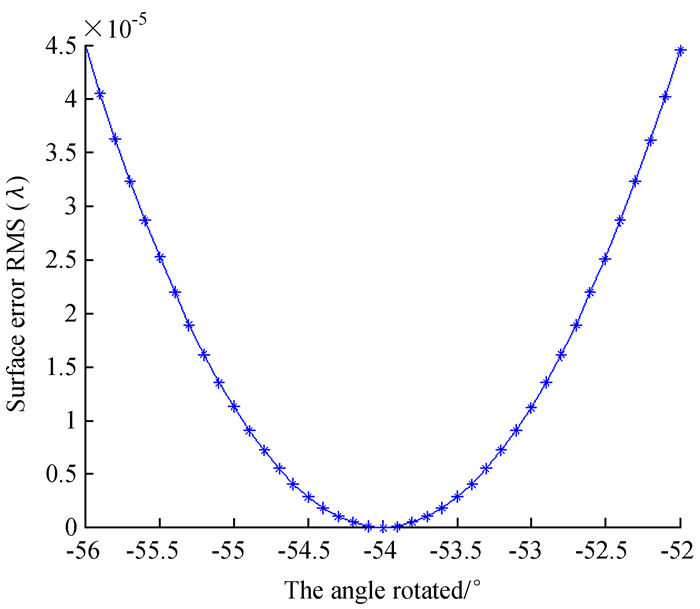
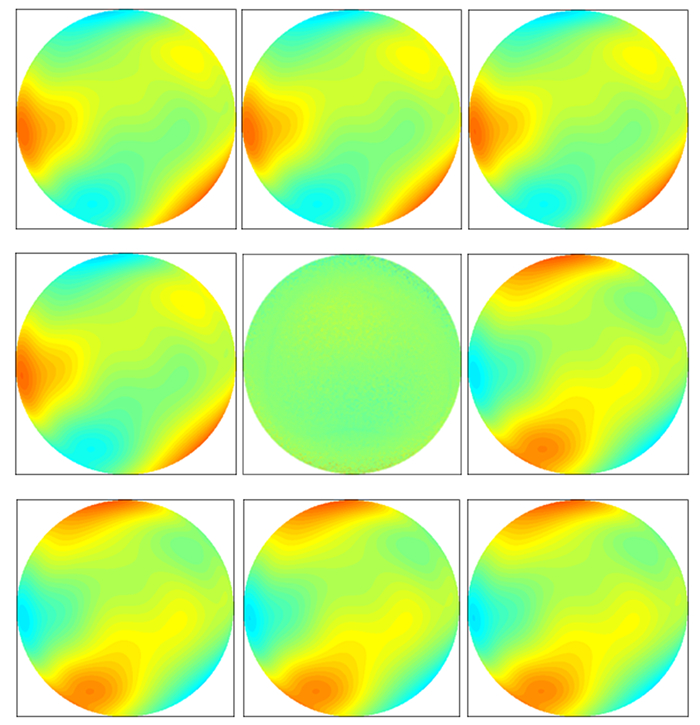
图 10和图 11分别给出了旋转偏差角度为-2°、-1.5°、-1°、-0.5°、0°、0.5°、1°、1.5°、2°的面形与理论相差的均方根曲线和面形偏差图,从图中可以看出,首先,偏差角度的绝对值越大,引入的面形误差越大;其次,偏差角度的绝对值影响面形误差的大小,旋转方向(逆时针旋转用负号)决定面形误差相对于原面形的凹凸。例如,偏差角度为-2°和2°的两个图形可以看出,偏差为-2°颜色深的区域正好对应偏差为2°的浅色区域。
|
| 图 10 不同旋转角度误差对应的拟合的A面的均方根值 Figure 10 RMS of face A after fitting with different rotation angle error |
|
| 图 11 旋转偏差角度-2°、-1.5°、-1°、-0.5°、0°、0.5°、1°、1.5°、2°的面形误差 Figure 11 Surface error with rotation angle of deviation -2°、-1.5°、-1°、-0.5°、0°、0.5°、1°、1.5°and 2° |
原A面形的均方根值是0.019 3 λ,含有2°旋转角度偏差的A面形的均方根值为0.019 7 λ,二者均方根值相差在万分之一波长的量级。当然对于高精度的测量,仅仅看均方根值是不可信的,从图 11可以看出,当旋转角度偏差的绝对值为0.5°的范围内,面形偏差相当小,而此时的均方根值小于百万分之一波长。
3.2.2 平移对准误差分析本文所述的实验方案中,第1块平晶Ⅰ,即干涉仪的标准平晶,在4次测试中不动,仅对平晶Ⅱ进行了移动,分析平移方向时,可以以标准平晶Ⅰ为参考,设置平晶Ⅱ的平移方向上的对准误差值[10]。由于分析的平晶是旋转对称的,所以本文将对准误差设置在y方向,即竖直方向。当两个面在竖直方向偏差y,则两个面平移对准误差值为2y。平晶口径为900 mm,分别分析当竖直方向偏差为1 mm、2 mm、3 mm、4 mm、5 mm时,即对准误差值为2 mm、4 mm、6 mm、8 mm、10 mm时,对面形拟合结果的影响。
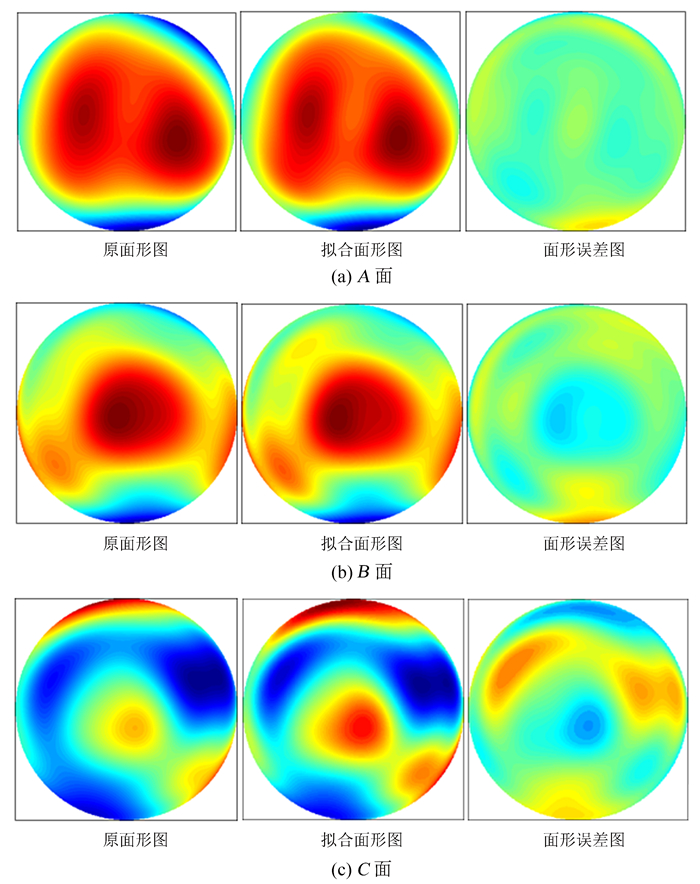
图 12给出了平移对准误差值为4 mm时,A、B、C面的面形和原面形对比,并相减得到面形误差图。从3个面的面形误差图可以看出,平移对准误差对于C面的影响相对于其余两个面较大。从各个面的面形误差图的均方根值定量分析,如表 3。分析表 3可以得出,首先,当平移对准误差值增加时,对于A、B、C3面的测量引入的误差值也在增加,其中C面的影响最大,其次是B面,影响最小的是A面。这对标定干涉仪标准平晶A面的面形误差非常有益;其次,y轴平移对准误差值为4 mm时(平晶口径为900 mm),拟合的A、B、C面形数据和原面形像差的均方根值都在千分之一波长。当大于4 mm,则精度较低。
|
| 图 12 平移对准误差值为4 mm时,各面的面形情况 Figure 12 Face image with a translation alignment error of 4 mm |
| y轴对准误 差值/mm |
均方根值(RMS)/λ | ||
| A | B | C | |
| 10 | 0.002 4 | 0.011 3 | 0.440 8 |
| 8 | 0.001 6 | 0.006 9 | 0.082 4 |
| 6 | 0.001 0 | 0.003 9 | 0.021 0 |
| 4 | 0.000 6 | 0.002 0 | 0.005 2 |
| 2 | 0.000 3 | 0.000 9 | 0.001 1 |
双平晶互检法理论所得的面形数据与原面形数据完全一致,由此验证了双平晶互检法在光学平面的绝对检验上完全正确可行。分析了在实验中,泽尼克多项式项数、旋转对准误差和平移对准误差对实验结果的影响,从而得出在实验结果要求的精度允许下的对准误差值大小。本文研究的方法主要为大口径平面光学元件高精度测量提供理论基础,并为研制超大口径平面干涉仪及其参考平晶误差标定问题提供技术积累。
| [1] | 刘晓梅.光学平面的绝对检验[D].南京:南京理工大学, 2004:3-5. |
| [2] | Rayleigh. Interference bands and their applications[J]. Nature , 1893 , 48 : 212 –214. |
| [3] | Schulz G, Schwider J, Hiller C, et al. Establishing an optical flatness stardard[J]. Applied Optics , 1971 , 10 (4) : 929 –934. DOI: 10.1364/AO.10.000929 |
| [4] | Fritz B S. Absolute calibration of an optical flat[J]. Optical Engineering , 1984 , 23 (4) : 379 –383. |
| [5] | Ai C, Wyant J C. Absolute testing of flats by using even and odd functions[J]. Applied Optics , 1993 , 32 (25) : 4698 –4705. DOI: 10.1364/AO.32.004698 |
| [6] | Freischlad K R. Absolute interferometric testing based on reconstruction of rotational shear[J]. Applied Optics , 2001 , 40 (10) : 1637 –1648. DOI: 10.1364/AO.40.001637 |
| [7] | Xu Chen, Chen Lei, Yin Jiayi. Method for absolute flatness measurement of optical surfaces[J]. Applied Optics , 2009 , 48 (13) : 2536 –2541. DOI: 10.1364/AO.48.002536 |
| [8] |
姚绘玲, 金振宇, 向永源. 大气色散对太阳多波段同步高分辨率图像重建的影响[J]. 天文研究与技术
, 2015 , 12 (2) : 189 –191 Yao Huiling, Jin Zhenyu, Xiang Yongyuan. A study of influence of atmospheric dispersion on the multi-waveband synchronous high-resolution reconstruction applied to solar images[J]. Astronomical Research & Technology , 2015 , 12 (2) : 189 –191. |
| [9] |
顾伯忠, 左恒. 云南天文台1 m红外望远镜的主镜热力学分析[J]. 天文研究与技术-国家天文台台刊
, 2008 , 5 (1) : 83 –85 Gu Bozhong, Zuo Heng. The thermal analysis of the primary mirror of 1 m infared solar telescope at Yunnan Observatory[J]. Astronomical Research & Technology-Publications of National Astronomical Observatories of China , 2008 , 5 (1) : 83 –85. |
| [10] | Malacara D. Optical Shop Testing[M]. 3rd ed Canada: John Wilrey & Sons. 2007, 498-543. |



