2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
激光测距技术是一项综合技术,涵盖激光、电子、微光探测、自动控制、精密光学机械、天文测量和卫星轨道计算等多个学科领域[1]。它通过精确测定激光脉冲从测站到目标的往返飞行时间t,结合光速c,就可获得测站到目标的距离R=ct/2。激光测距在实际工作中是一个非常复杂的过程,受激光光束的发散角、大气湍流、大气传输特性[2-3]、目标特性[4]、望远镜指向误差[5-6]、距离[7]、接收孔径大小等多种因素的影响,其中任何一个相关因数的变化都会引起激光测距中回波光子数的变化。因此,分析研究回波光子随上述各因素的变化规律,对激光测距理论研究、系统性能评估以及系统设计具有重要意义。
Matlab是世界上使用最为广泛的数学软件之一,它具有强大的数值计算、数据处理、系统分析、图形显示、符号运算等功能,是一个完整的数学平台[8]。本文利用Matlab平台开发了用户应用界面,估算上述多种因素对激光测距系统回波光子的影响,通过设置测距系统的相关参数(例如测距波长、能量、接收口径等)可方便直观地对激光测距回波光子分布特性进行分析研究,为测距系统的设计提供理论依据。
1 回波光子数估算 1.1 激光测距方程设测距激光器发射的单个激光脉冲能量为Et,波长为λ,普朗克常数为h,光速为c,激光器的发射增益为Gt,发射系统的发射效率为ηt,则从地面测距系统发射的单个激光脉冲的光子数为
| $ {{n}_{\text{s}}}=\left( {{E}_{\text{t}}}\frac{\lambda }{hc} \right){{\eta }_{\text{t}}}{{G}_{\text{t}}}\frac{\sigma }{\pi {{({{\theta }_{\text{d}}}R+r)}^{2}}}\frac{{{A}_{\text{r}}}}{\pi {{({{\theta }_{\text{m}}}R)}^{2}}}\rho {{\eta }_{\text{r}}}{{T}_{\text{a}}}^{2}{{T}_{\text{c}}}^{2}. $ | (1) |
假设激光器发射的激光为高斯光束,则高斯光束的发射增益Gt可表示如下[9-11]:
| $ {{G}_{\text{t}}}=\frac{8}{{{\theta }_{\text{d}}}^{2}}\text{ }\!\!~\!\!\text{ exp}\left[~-2{{\left( \frac{{{\theta }_{\text{p}}}}{{{\theta }_{\text{d}}}} \right)}^{2}} \right], $ | (2) |
其中,θd是激光束的发散半角;θp是激光束的指向误差。
ns是在没考虑指向误差情况下的平均回波光子数,当考虑指向误差时,单个脉冲的平均回波光子数为[9]:
| $ \left\langle {{n}_{\text{s}}} \right\rangle ={{n}_{\text{s}}}\int\limits_{-\infty }^{\infty }{\text{d(}\delta \alpha \text{)}p\text{(}\delta \alpha \text{)}}\int\limits_{-\infty }^{\infty }{\text{d(}\delta \beta \text{)}p\text{(}\delta \beta \text{)}}\exp \left[-2{{\left( \frac{\alpha +\delta \alpha +\beta +\delta \beta }{{{\theta }_{\text{d}}}} \right)}^{2}} \right], $ | (3) |
其中,α、β分别为方位、俯仰指向偏差;δα、δβ分别为方位、俯仰实时随机误差;p(δα)、p(δβ)分别为方位、俯仰随机指向误差的概率分布函数。
假设p(δα)、p(δβ)均是高斯函数,则:
| $ p\text{(}\delta \alpha )=\sqrt{\frac{2}{\pi }}\frac{1}{{{\theta }_{\alpha }}}\exp \left[-2{{\left( \frac{\delta \alpha }{{{\theta }_{\alpha }}} \right)}^{2}} \right], $ | (3-1) |
| $ p\text{(}\delta \beta )=\sqrt{\frac{2}{\pi }}\frac{1}{{{\theta }_{\beta }}}\exp \left[-2{{\left( \frac{\delta \beta }{{{\theta }_{\beta }}} \right)}^{2}} \right], $ | (3-2) |
其中,θα、θβ分别为望远镜的方位、俯仰跟踪误差。
将(3-1)、(3-2)式代入(3)式,得到:
| $ \langle {{n}_{\text{s}}}\rangle ={{n}_{\text{s}}}\frac{{{\theta }_{_{\text{d }\!\!\alpha\!\!\text{ }}}}{{\theta }_{_{\text{d }\!\!\beta\!\!\text{ }}}}}{{{\theta }_{\text{ }\!\!\alpha\!\!\text{ }}}{{\theta }_{\text{ }\!\!\beta\!\!\text{ }}}}\text{ }\!\!~\!\!\text{ exp}~\left[-2\left( \frac{{{\alpha }^{2}}+{{\beta }^{2}}}{{{\theta }_{\text{d}}}^{2}} \right) \right]\text{ }\!\!~\!\!\text{ exp}~\left[\frac{2}{{{\theta }_{\text{d}}}^{4}}({{\alpha }^{2}}{{\theta }_{\text{d }\!\!\alpha\!\!\text{ }}}^{2}+{{\beta }^{2}}{{\theta }_{\text{d }\!\!\beta\!\!\text{ }}}^{2}) \right], $ | (4) |
此处定义:
| $ \frac{1}{{{\theta }_{\text{d }\!\!\alpha\!\!\text{ }}}^{2}}=\frac{1}{{{\theta }_{\text{d}}}^{2}}+\frac{1}{{{\theta }_{\text{ }\!\!\alpha\!\!\text{ }}}^{2}}, $ | (4-1) |
| $ \frac{1}{{{\theta }_{\text{d }\!\!\beta\!\!\text{ }}}^{2}}=\frac{1}{{{\theta }_{\text{d}}}^{2}}+\frac{1}{{{\theta }_{\text{ }\!\!\beta\!\!\text{ }}}^{2}}. $ | (4-2) |
在不考虑指向偏差时,即α=β=0,(4)式可简化为
| $ \langle {{n}_{\text{s}}}\rangle ={{n}_{\text{s}}}\frac{{{\theta }_{\text{d }\!\!\alpha\!\!\text{ }}}{{\theta }_{\text{d }\!\!\beta\!\!\text{ }}}}{{{\theta }_{\text{ }\!\!\alpha\!\!\text{ }}}{{\theta }_{\text{ }\!\!\beta\!\!\text{ }}}}. $ | (5) |
如果望远镜方位、俯仰跟踪误差概率分布相同,即θα=θβ=θj,则(5)式可表示为
| $ \langle {{n}_{\text{s}}}\rangle ={{n}_{\text{s}}}\frac{{{\theta }_{\text{dj}}}^{2}}{{{\theta }_{\text{j}}}^{2}}={{n}_{\text{s}}}\frac{1}{1+\frac{{{\theta }_{\text{j}}}^{2}}{{{\theta }_{\text{d}}}^{2}}}. $ | (6) |
其中,θj是望远镜的跟踪误差。
将(1)、(2)式代入(6)式,得到单个激光脉冲在接收器光敏面上产生的平均回波光子数方程为
| $ \begin{align} & \langle {{n}_{\text{s}}}\rangle =\left( {{E}_{\text{t}}}\frac{\lambda }{hc} \right){{\eta }_{\text{t}}}\frac{\sigma \rho }{\pi {{({{\theta }_{\text{d}}}R+r)}^{2}}}\frac{8}{{{\theta }_{\text{d}}}^{2}}\text{exp}~\left[-2{{\left( \frac{{{\theta }_{\text{p}}}}{{{\theta }_{\text{d}}}} \right)}^{2}} \right]\left[\frac{1}{1+{{\left( \frac{{{\theta }_{\text{j}}}}{{{\theta }_{\text{d}}}} \right)}^{2}}} \right] \\ & \frac{{{A}_{\text{r}}}}{\pi {{({{\theta }_{\text{m}}}R)}^{2}}}{{\eta }_{\text{r}}}{{T}_{\text{a}}}^{2}{{T}_{\text{c}}}^{2}. \\ \end{align} $ | (7) |
激光束在大气中传输时,不只受大气散射和吸收的影响,还受大气湍流的影响,当激光束在大气湍流中传输时,由于大气折射率的随机起伏,光束的波前相位发生畸变,从而产生光束扩展、漂移及光强闪烁等现象[12]。
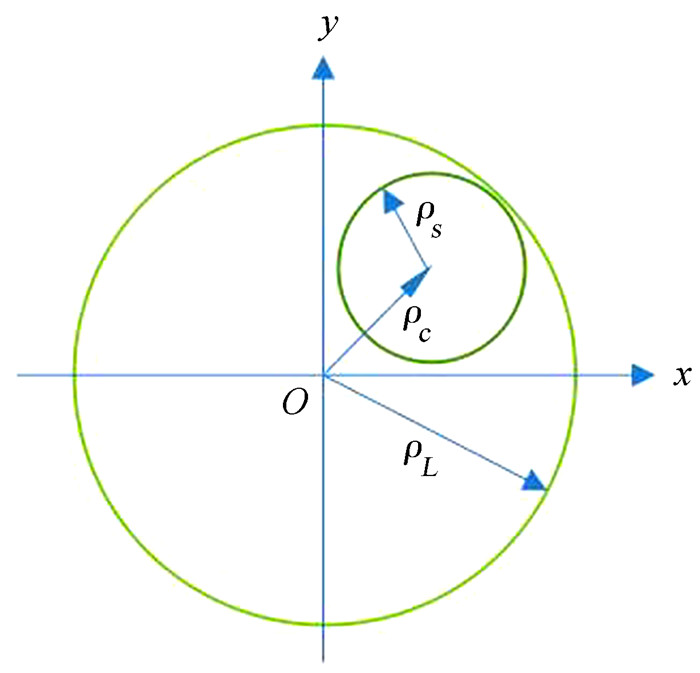
当激光束沿Z轴在大气中传输时,对垂直于Z轴且在Ro处的一平面取一个曝光非常短的光斑图像如图 1,一个半径为ρs的扩展了的光斑,光斑漂移至距原中心O为ρc处,当观测时间较长时,众多短期项漂移量ρc和扩展量ρs综合效应表现为长期项扩展ρL,其均方值为[9, 13]
|
| 图 1 远场处的光斑分布 Figure 1 Intensity distribution in the far field |
| $ \langle {{\rho }_{\text{L}}}^{2}\rangle =\langle {{\rho }_{\text{c}}}^{2}\rangle +\langle {{\rho }_{\text{s}}}^{2}\rangle, $ | (8) |
〈ρL2〉定义为
| $ \langle {{\rho }_{\text{L}}}^{2}\rangle =\frac{\iint{{{\text{d}}^{2}}\rho \rho {{\Gamma }_{2}}(z,\rho ,\rho )}}{\iint{{{\text{d}}^{2}}\rho {{\Gamma }_{2}}(z,\rho ,\rho )}}. $ | (9) |
在z=0平面上的初始高斯光场分布uo(ρ′)为
| $ {{u}_{\text{o}}}({\rho }')={{e}^{\left(-\frac{{{{{\rho }'}}^{2}}}{2{{r}^{2}}}-\frac{ik{{{{\rho }'}}^{2}}}{2F} \right)}}, $ | (10) |
其中,r为光束的初始半径;F为曲率半径。
| $ \begin{gathered} {\mathit{\Gamma} _2}({R_{\text{o}}},{\rho _1},{\rho _2}) = {\left( {\frac{k}{{2\pi {R_{\text{o}}}}}} \right)^2}\iint {{{\text{d}}^2}{{\rho '}_{_1}}}\iint {{{\text{d}}^2}{{\rho '}_{_2}}{u_{\text{o}}}({{\rho '}_1}){u_{\text{o}}}^ * ({{\rho '}_{_2}})}.\; \hfill \\ {\text{exp}}\left\{ \begin{gathered} \frac{{ik}}{{2{R_{\text{o}}}}}[{({\rho _1} - {{\rho '}_1})^2} - {({\rho _2} - {{\rho '}_2})^2}] \hfill \\ \frac{{\;\; - \pi {k^2}}}{4}\int\limits_0^{R{\text{o}}} {{\text{d}}R'H} \left[ {R\prime ,\frac{{R\prime }}{{{R_{\text{o}}}}}({\rho _1} - {\rho _2}) + (\rho {\prime _1} - \rho {\prime _2})\left( {1 - \frac{{R\prime }}{{{R_{\text{o}}}}}} \right)} \right] \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered} $ | (11) |
将(10)式代入(11)式,可以得到:
| $ \langle {{\rho }_{\text{L}}}^{2}\rangle \approx \frac{{{R}_{\text{o}}}^{2}}{{{k}^{2}}{{r}^{2}}}+{{r}^{2}}{{\left( 1-\frac{{{R}_{\text{o}}}}{F} \right)}^{2}}+\frac{17.6{{R}_{\text{o}}}^{2}}{{{k}^{2}}{{r}_{\text{o}}}^{2}},$ | (12) |
其中,ro为大气相干长度;波数k=2π/λ;Ro为光束受大气湍流影响的传输距离。
由于短期项漂移与扩展体现的是大气湍流对激光束的实时效应,而长期项扩展是包括短期项漂移与扩展的综合效应,因此本文用大气湍流对激光束的长期项扩展来分析激光测距中回波光子数。长期项扩展的半径为
| $ \begin{align} & \langle {{n}_{\text{s}}}\rangle =\left( {{E}_{\text{t}}}\frac{\lambda }{hc} \right)\frac{{{\eta }_{\text{t}}}\sigma \rho }{\pi {{({{\theta }_{\text{d}}}R+r+\sqrt{\langle {{\rho }_{\text{L}}}^{2}\rangle })}^{2}}}\frac{8}{{{\theta }_{\text{d}}}^{2}}~\text{exp}\left[-2{{\left( \frac{{{\theta }_{\text{p}}}}{{{\theta }_{\text{d}}}} \right)}^{2}} \right]~\left[\frac{1}{1+{{\left( \frac{{{\theta }_{\text{j}}}}{{{\theta }_{\text{d}}}} \right)}^{2}}} \right] \\ & \frac{{{A}_{\text{r}}}{{\eta }_{\text{r}}}}{\pi {{({{\theta }_{\text{m}}}R)}^{2}}}{{T}_{\text{a}}}^{2}{{T}_{\text{c}}}^{2}. \\ \end{align} $ | (13) |
能见度是以气象能见距离度量的[15]。气象能见距离是指正常视力的人在当时天气条件下,能够从天空背景中看到和辨认目标物(黑色,大小适度)的最大水平距离[16]。用经验公式确定的大气衰减计算公式为[17-19]
| $ {{\beta }_{\text{a}}}=\frac{3.91}{{{V}_{\text{a}}}}{{\left( \frac{\lambda }{0.55} \right)}^{-q}}, $ | (14) |
其中,Va和λ的单位分别为km和μm;当大气能见度Va < 6 km时,q=0.585Va1/3;中等能见度时,q=1.3;当能见度Va> 80 km时,q=1.6。所以大气透过率Ta为
| $ {{T}_{\text{a}}}=1-{{\beta }_{\text{a}}}. $ | (15) |
厚积云的存在限制了光波长的范围,对于总光学厚度小于0.5的云层,波长范围从0.317 μ到12 μ的卷云透过率的计算公式为[9]
| $ {{T}_{\text{c}}}=\text{exp }\!\![\!\!\text{ }-0.14{{({{t}_{\text{c}}}\text{sec}{{\theta }_{\text{a}}})}^{2}}\text{ }\!\!]\!\!\text{, } $ | (16) |
其中,tc为平均卷云厚度;θa为天顶角。
将(14~16)式代入(13)式,得到单个激光脉冲在接收器光敏面上产生的平均回波光子数方程为
| $ \begin{align} & \langle {{n}_{\text{s}}}\rangle =\left( {{E}_{\text{t}}}\frac{\lambda }{hc} \right){{\eta }_{\text{t}}}\frac{8}{{{\theta }_{\text{d}}}^{2}}\text{ }\!\!~\!\!\text{ exp}\left[-2{{\left( \frac{{{\theta }_{\text{p}}}}{{{\theta }_{\text{d}}}} \right)}^{2}}-0.28{{({{t}_{\text{c}}}\text{sec}{{\theta }_{\text{a}}})}^{2}} \right]\left[\frac{1}{1+{{\left( \frac{{{\theta }_{\text{j}}}}{{{\theta }_{\text{d}}}} \right)}^{2}}} \right] \\ & \left( 1-\frac{3.91}{{{V}_{\text{a}}}}{{\left( \frac{\lambda }{0.55} \right)}^{-q}} \right){{~}^{2}}\frac{\sigma \rho }{\pi {{({{\theta }_{\text{d}}}R+r+\sqrt{\langle {{\rho }_{\text{L}}}^{2}\rangle })}^{2}}}\frac{{{A}_{\text{r}}}{{\eta }_{\text{r}}}}{\pi {{({{\theta }_{\text{m}}}R)}^{2}}}. \\ \end{align} $ | (17) |
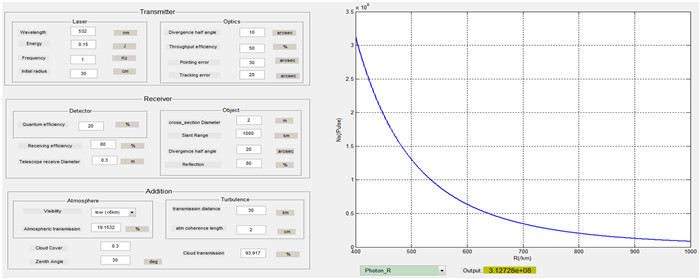
由1.1节可见,测距回波光子分布受多种因素的影响,实际的激光测距过程极其复杂。为了更好地对测距回波光子分布特性进行分析与研究,利用Matlab平台下的图形用户界面(Graphical User Interface, GUI)开发了激光测距回波光子分布特性分析软件,分析研究并实时显示诸因素对回波光子数的影响。软件界面包括:发射系统(如激光能量、波长、发散角、指向偏差、望远镜的跟踪误差等),接收系统(如望远镜有效接收口径、目标有效光学直径、角反射器反射回测站的光束发散角、目标距离等),大气和云层透过率,湍流等因素,相关图形和结果显示项等,如图 2、图 3。
|
| 图 2 回波光子数与距离的关系图 Figure 2 Echo photon number variation as a function of distance |
|
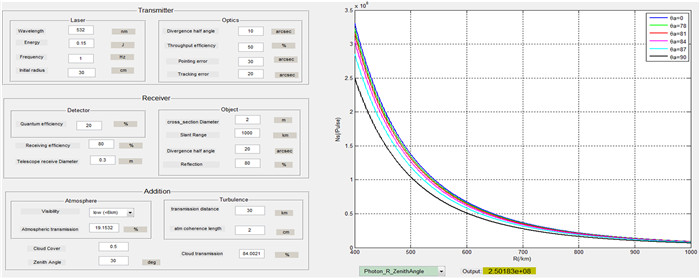
| 图 3 不同天顶角时回波光子数与距离的关系图 Figure 3 Echo photon number variation as a function of distance under the condition of different zenith angles |
平均回波光子数和目标距离的关系如图 2。在其它各参数相同的情况下,探测到的回波光子数随距离的增大而减少;当修改任一参数时,回波光子数将作相应的改变。
在界面上可以便捷地选择输出不同的关系图,以图 3不同天顶角情况下回波光子数与距离的关系为例,由于随着海拔高度的升高,大气的衰减系数降低,因此,在地面激光测距时,沿竖直方向的探测距离要比沿水平方向大得多。沿各个不同天顶角探测到的平均回波光子数随距离的变化由图可知:在大气条件相同的情况下,沿竖直方向和水平方向探测到的平均回波光子数的差别随距离的增大而减小。当探测距离相同时,天顶角从0°(竖直方向)到90°(水平方向)变化的过程中,在天顶角较小时,随着天顶角的增大,回波光子数减少较慢。当天顶角较大时,随着天顶角的增大,回波光子数减少很快。这主要是受大气中气溶胶对光的吸收和散射的影响[20]。软件根据(17)式编写,综合考虑多种因素,具有较强的通用性。
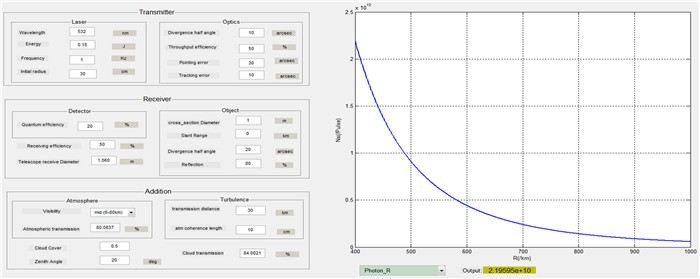
2 测距系统回波光子数估算以云南天文台1.2 m望远镜原有的激光测距系统为例,估算测距系统回波光子数。系统参数[13, 21]:单个激光脉冲的能量Et是0.15 J,波长λ是532 nm,激光束的初始半径r是30 cm,激光发射系统的发射效率ηt是0.5,激光束的发散半角θd是10″,激光束的指向误差Δθp是30″,望远镜的跟踪误差Δθj是10″,目标的有效光学直径Do是1 m,角反射器反射回测站的光束发散半角θm是20″,目标的反射率ρ是0.8,望远镜有效口径Dr是1.060 m,光束受大气湍流影响的传输距离Ro是30 km,大气相干长度ro是10 cm,接收系统的接收效率ηr是0.5,激光穿过大气的单程透过率Ta是0.8,激光穿过云层的单程透过率Tc是0.84。由图 4可知,测站到目标的距离R范围为400 km到1 000 km时,得到的平均回波光子数约为2.1 × 1010。
|
| 图 4 回波光子数与距离的关系图 Figure 4 Echo photon number variation as a function of distance |
本文较全面地考虑了影响激光测距的各种因素,给出了测距方程较详细的推导和表达式,并对测距中回波光子数进行了理论分析和估算;利用Matlab平台编制了一套关于激光测距系统回波光子分布特性的通用分析软件,在界面上可以针对不同的测距系统便捷地调整每个相关参数,还可以通过关系图更直观地对系统的各相关参数和回波光子数进行总体分析,从而为探测器的选择及测距系统的设计提供理论依据。在今后的工作中将对探测器和测距系统进行相关的分析和研究;在实际工作中,由于激光测距过程的复杂性,将对软件部分参数做深一步的探讨,对系统进行进一步优化。
| [1] |
叶叔华, 黄珹. 天文地球动力学[M].
山东: 山东科学技术出版社. 2000.
|
| [2] |
付强, 姜会林, 王晓曼. 激光在大气中传输特性的仿真研究[J]. 空军工程大学学报:自然科学版
, 2011 , 12 (2) : 57 –61 Fu Qiang, Jiang Huilin, Wang Xiaoman. Study of laser transmission characteristics in atmosphere by simulation[J]. Journal of Air Force Engineering University:Natural Science Edition , 2011 , 12 (2) : 57 –61. |
| [3] |
严卫, 张日伟, 代登坡, 等. 激光大气传输特性及其回波信号仿真研究[J]. 电波科学学报
, 2012 , 27 (3) : 564 –571 Yan Wei, Zhang Riwei, Dai Dengpo, et al. Simulation research on the atmospheric transmission characteristics and the return signal for laser[J]. Chinese Journal of Radio Science , 2012 , 27 (3) : 564 –571. |
| [4] |
张雷洪, 杨艳, 臧华国, 等. 目标反射特性对激光测距的影响[J]. 中国激光
, 2008 , 35 (7) : 1001 –1004 Zhang Leihong, Yang Yan, Zang Huaguo, et al. Reflective characteristics of target in laser rangefinder[J]. Chinese Journal of Lasers , 2008 , 35 (7) : 1001 –1004. DOI: 10.3788/JCL |
| [5] |
瞿锋, 卫志斌, 程伯辉, 等. 恒星跟踪与人卫激光测距仪望远镜指向修正[J]. 测绘科学
, 2004 , 29 (2) : 55 –56 |
| [6] |
黄宝利, 韩兴伟, 张楠, 等. 卫星激光测距系统的指向偏差修正[J]. 激光与红外
, 2014 , 44 (7) : 715 –719 Huang Baoli, Han Xingwei, Zhang Nan, et al. Axis correction of satellite laser ranging system based on image processing technique[J]. Laser & Infrared , 2014 , 44 (7) : 715 –719. |
| [7] |
李语强, 李荣旺, 李祝莲, 等. 非合作目标分光路激光测距中距离值的确定方法[J]. 天文研究与技术——国家天文台台刊
, 2012 , 9 (2) : 137 –142 Li Yuqiang, Li Rongwang, Li Zhulian, et al. Determination of the distance to a non-coorperative target in laser ranging with separate optical paths[J]. Publications of the Yunnan Observatory——Publications of National Astronomical Observatories of China , 2012 , 9 (2) : 137 –142. |
| [8] |
宋敏, 王江, 杨向东, 等. 激光测距参数分析软件的设计[J]. 激光杂志
, 2004 , 25 (2) : 55 –56 Song Min, Wang Jiang, Yang Xiangdong, et al. Designing the laser measurement parameter[J]. Laser Journal , 2004 , 25 (2) : 55 –56. |
| [9] | Degnan J J. Millimeter accuracy satellite laser ranging:a review[J]. Contributions of Space Geodesy to Geodynamics:Technology , 1993 : 133 –162. |
| [10] | Degnan J J. Theoretical performance of NASA's SGSLR system ranging to GNSS Satellites[C]//Sigma Space Corporation ILRS Technical Workshop. 2015. |
| [11] | Ndlovu S C, Combrinck L, Exertier P, et al. An estimation of the number of expected returned photons for the HartRAO Lunar Laser Ranger system[C]//19th International Workshop on Laser Ranging. 2011. |
| [12] |
柯熙政, 王婉婷. 部分相干光在斜程和水平大气湍流中的光强与扩展[J]. 应用科学学报
, 2015 , 33 (2) : 142 –154 Ke Xizheng, Wang Wanting. Intensity and expansion of partially coherent beam propagating in slant and horizontal atmospheric turbulence[J]. Journal of Applied Sciences , 2015 , 33 (2) : 142 –154. |
| [13] | 熊耀恒.月球激光测距的新技术方法研究[D].昆明:中国科学院国家天文台云南天文台, 2001. |
| [14] | Fante R L. Electromagnetic beam propagation in turbulent media[J]. Proceedings of the IEEE , 1976 , 63 (12) : 1669 –1692. |
| [15] |
李景真, 苏世学, 赵俊民. 光学手册[M].
北京: 清华大学出版社. 1998.
|
| [16] |
戴阳, 程学武, 李发泉, 等. 目标反射特性与激光测距回波强度关系的研究[J]. 激光杂志
, 2007 , 28 (3) : 83 –84 Dai Yang, Cheng Xuewu, Li Faquan, et al. Study on the relationship of return power with different reflection model of object in laser ranging[J]. Laser Journal , 2007 , 28 (3) : 83 –84. |
| [17] |
蓝信钜. 激光技术[M].
北京: 科学出版社. 2000.
|
| [18] |
王海先, 叶艾. 大气衰减系数对激光测距能力影响的研究[J]. 舰船科学技术
, 2007 , 29 (6) : 116 –119 Wang Haixian, Ye Ai. The influence of the coefficient of atmospheric attenuation to the capability of laser ranging[J]. Ship Science and Technology , 2007 , 29 (6) : 116 –119. |
| [19] |
郭豪, 邱琪, 马娜, 等. 不同能见度下激光测距仪最大测程的数值算法[J]. 红外与激光工程
, 2013 , 42 (12) : 3330 –3334 Guo Hao, Qiu Qi, Ma Na, et al. Numerical algorithm for maximum range of laser rangefinder in different visibility[J]. Infrared and Laser Engineering , 2013 , 42 (12) : 3330 –3334. |
| [20] |
赵少卿, 张雏. 激光大气传输特性仿真及对激光测距的影响[J]. 激光与光电子学进展
, 2013 (11) : 55 –60 Zhao Shaoqing, Zhang Chu. Simulation on atmospheric transmission characteristic of laser and its impact on laser ranging[J]. Laser & Optoelectronics Progress , 2013 (11) : 55 –60. |
| [21] |
李祝莲, 熊耀恒, 何妙婵, 等. 云南天文台人造卫星激光测距系统原理[J]. 天文研究与技术——国家天文台台刊
, 2008 , 5 (3) : 248 –252 Li Zhulian, Xiong Yaoheng, He Miaochan, et al. Principle of 1.2m telescope Satellite Laser Ranging system[J]. Publications of the Yunnan Observatory——Publications of National Astronomical Observatories of China , 2008 , 5 (3) : 248 –252. |



