激光测距方程是研究激光测距系统探测能力的基本理论依据，对激光测距方程进行分析能够对测距系统中使用的激光器的能量、激光发散角等参数的最优选取提供理论支持。传统激光测距方程的推导过程中假设激光脉冲能量的空间分布是均匀的，在激光大气传播过程中仅考虑了大气的衰减作用^[1]。然而，在激光测距系统中，激光能量的分布形式，大气湍流对激光传输时抖动、扩展、闪烁以及望远镜在实测时的跟踪抖动都会导致回波强度的变化。文[2]在传统激光测距方程的基础上，考虑了激光束本身的分布形式和大气湍流对激光传输的影响，推导出激光测距方程的新的表达形式；文[3]基于对望远镜跟踪抖动满足高斯分布的假设，推导出含有望远镜跟踪抖动参量的激光测距方程。在实测过程中，大气湍流引起光束的抖动、扩展、闪烁以及望远镜的跟踪抖动同时影响回波强度，所以需将大气湍流与望远镜跟踪抖动同时考虑到激光测距方程中。

1 激光能量为高斯(Gaussian)分布时能量表达式

在激光测距系统中使用的激光器，其光谐振腔发出的基模辐射场的横截面振幅与能量是高斯分布。激光束在传输距离为z时能量分布E(ρ)和截面半径$|\rho |=\rho \left( x, y \right)=\sqrt{{{x}^{2}}+{{y}^{2}}} $之间的关系为

$ E(\rho )=A{{e}^{-\frac{{{\rho }^{2}}}{\omega {{\left( z \right)}^{2}}}}}, $

(1)

其中，A为系数；ω(z)为表征激光传输距离z时的光斑半径

$ \omega {{\left( z \right)}^{2}}={{\omega }_{0}}^{2}[1+{{(\frac{\lambda z}{\pi {{\omega }_{0}}^{2}})}^{2}}], $

(2)

其中，w₀为激光的束腰半径；z为激光传输的距离。

假设光束中心能量的1/e处所对应的光束半径为ρ_e，故有

$ \frac{{{\rho }_{e}}^{2}}{\omega {{\left( z \right)}^{2}}}=1~. $

(3)

将(3)式代入(1)式：

$ E\left( \rho \right)=A{{e}^{-\frac{{{\rho }^{2}}}{{{\rho }_{\rm{e}}}^{2}}}}. $

(4)

对(4)式进行积分可求出激光束能量分布E(ρ)与整个激光脉冲能量E₀的关系式：

$ {{E}_{0}}=\iint{E\left( \rho \right)\rho \text{d}\rho \text{d}\varphi }=A\int\limits_{0}^{2\pi }{\text{d}\varphi }\int\limits_{0}^{\infty }{{{e}^{-\frac{{{\rho }^{2}}}{{{\rho }_{\rm{e}}}^{2}}}}\rho \text{d}\rho =\pi A{{\rho }_{\text{e}}}^{2}}\Rightarrow A=\frac{{{E}_{0}}}{\pi {{\rho }_{\text{e}}}^{2}} $

那么，

$ E(\rho )=\frac{{{E}_{0}}}{\pi {{\rho }_{\text{e}}}^{2}}{{e}^{-\frac{{{\rho }^{2}}}{{{\rho }_{e}}^{2}}}}. $

(5)

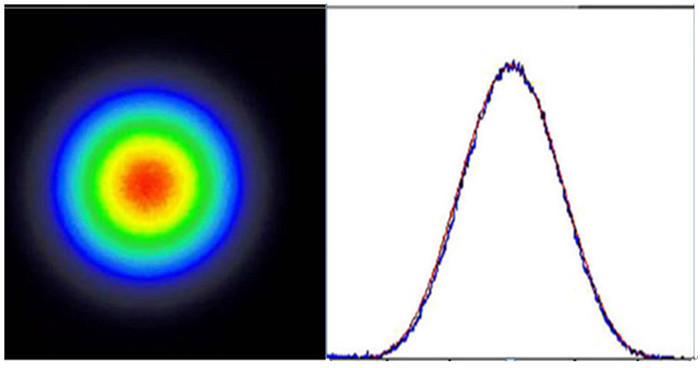
由(5)式可知，当空间碎片位于高斯光束中心时反射的回波强度最强，当空间碎片相对高斯光束中心存在偏差时，回波强度降低，激光能量为高斯分布时的示意图如图 1。

2 望远镜跟踪抖动导致目标偏离光束中心距离的概率分布表达式

假设望远镜的跟踪抖动$ {\vec{\phi }} $是满足高斯概率分布的随机变量，此时$ {\vec{\phi }} $可表示为

$ {{g}_{t}}(\vec{\phi };\vec{\mu }, \sum{_{1}})=\frac{1}{2\pi |\sum{_{1}}{{|}^{\frac{1}{2}}}}{{e}^{-\frac{1}{2}{{(\vec{\phi }-\vec{\mu })}^{\text{T}}}{{\sum{_{1}}}^{-1}}(\vec{\phi }-\vec{\mu })}}, $

(6)

其中，$ \vec{\phi }=({{\phi }_{x}}, {{\phi }_{y}}) $；ϕ_x为望远镜跟踪抖动$ {\vec{\phi }} $在方位轴上的分量；ϕ_y为望远镜跟踪抖动$ {\vec{\phi }} $在高度轴上的分量；$ \vec{\mu }=({{\mu }_{x}}, {{\mu }_{y}}) $为望远镜的固定指向偏差；μ_x为望远镜方位轴上的固定指向偏差；μ_y为望远镜高度轴上的固定指向偏差。

当望远镜不存在固定指向偏差时，有

$ {{g}_{t}}(\vec{\phi };0, \sum{_{1}})=\frac{1}{2\pi |\sum{_{1}}{{|}^{\frac{1}{2}}}}{{e}^{-\frac{1}{2}{{(\vec{\phi })}^{\text{T}}}{{\sum{_{1}}}^{-1}}(\vec{\phi })}}, $

(7)

其中，T为转置运算符；∑₁为$ {\vec{\phi }} $协方差矩阵，可表示为

$ \sum{_{1}}=\left( \begin{matrix} \sigma _{x_1}^{2} & {{\sigma }_{x_1y_1}} \\ {{\sigma }_{x_1y_1}} & \sigma _{y_1}^{2} \\ \end{matrix} \right). $

(8)

当望远镜的跟踪随机误差在高度和方位轴互不相关时有

$ \sum{_{1}}=\left( \begin{matrix} \sigma _{x_1}^{2} & 0 \\ 0 & \sigma _{y_1}^{2} \\ \end{matrix} \right). $

(9)

其中，σ_x1为望远镜在方位轴的跟踪精度；σ_y1为望远镜在高度轴的跟踪精度。

假设望远镜跟踪抖动为高斯分布且仅考虑望远镜跟踪随机误差，由望远镜跟踪抖动导致的空间目标偏离光束中心的距离$ {{{\vec{\rho }}}_{\text{t}}} $也是满足高斯分布的随机变量，$ {{{\vec{\rho }}}_{\text{t}}} $与$ {\vec{\phi }} $的关系可表示为

$ {{{\vec{\rho }}}_{\text{t}}}=\vec{\phi }R, $

(10)

R是望远镜与被测目标的距离。所以有

$ \vec{\phi }={{{\vec{\rho }}}_{\text{t}}}/R. $

(11)

将其代入(7)式可推出：

$ {{g}_{t}}({{{\vec{\rho }}}_{\text{t}}};0, \sum{_{12}})=\frac{1}{2\pi |\sum{{{_{1}}^{\prime }}}{{|}^{\frac{1}{2}}}}{{e}^{-\frac{1}{2}{{({{{\vec{\rho }}}_{\text{t}}})}^{T}}{{\sum{_{1}}}^{\prime }}^{-1}({{{\vec{\rho }}}_{\text{t}}})}}, $

(12)

其中，$ {{\sum{_{1}}}^{\prime }}=\left( \begin{matrix} \sigma _{x_1}^{2}{{R}^{2}} & 0 \\ 0 & \sigma _{y_1}^{2}{{R}^{2}} \\ \end{matrix} \right) $。

3 大气湍流作用导致的目标偏离光束中心距离的概率分布表达式

由于大气湍流的影响，激光在传播过程中不断随机地改变其波束特性，表现为光束的扩展、光斑漂移及脉冲宽度的增加等^[4]。光斑漂移导致空间碎片相对于光束的中心距离$\overrightarrow{{{\rho }_{\text{a}}}} $随机变化，假设随机变量$ \overrightarrow{{{\rho }_{\text{a}}}}$满足高斯概率分布函数g_a，g_a可表示成：

$ {{g}_{\text{a}}}(\overrightarrow{{{\rho }_{\text{a}}}};0, \sum{_{2}})=\frac{1}{2\pi |\sum{_{2}}{{|}^{\frac{1}{2}}}}{{e}^{-\frac{1}{2}{{(\overrightarrow{{{\rho }_{\text{a}}}})}^{\text{T}}}\sum{{{_{2}}^{-1}}}(\overrightarrow{{{\rho }_{\text{a}}}})}}, $

(13)

其中，$ \overrightarrow{{{\rho }_{\text{a}}}}=({{x}_{2}}, {{y}_{2}}) $；x₂为$ \overrightarrow{{{\rho }_{\text{a}}}} $在望远镜方位轴的分量；y₂为$ \overrightarrow{{{\rho }_{\text{a}}}} $在望远镜高度轴的分量；T为转置运算符；0代表光束的中心为随机变量$ \overrightarrow{{{\rho }_{\text{a}}}} $的均值；∑₂为$ \overrightarrow{{{\rho }_{\text{a}}}} $的协方差矩阵。当大气湍流引起的光斑漂移在望远镜方位和高度轴互不相关时有

$ \sum{_{2}}=\left( \begin{matrix} \sigma _{{{x}_{2}}}^{2} & 0 \\ 0 & \sigma _{{{y}_{2}}}^{2} \\ \end{matrix} \right), $

其中，σ_x2²为望远镜方位轴的光斑漂移方差；σ_y2²为望远镜高度轴的光斑漂移方差。

根据文[4]，大气湍流导致光束中心漂移的均方差为

$ <{{\rho }_{\text{c}}}^{2}>\approx \frac{10.22{{R}^{2}}}{{{k}^{2}}{{r}_{0}}^{\frac{5}{3}}{{D}^{\frac{1}{3}}}}. $

(14)

当光斑漂移方差在望远镜方位轴和高度轴相等时，可推出：

$ \sigma _{{{x}_{2}}}^{2}=\sigma _{{{y}_{2}}}^{2}=<{{\rho }_{\text{c}}}^{2}>\approx \frac{10.22{{R}^{2}}}{{{k}^{2}}{{r}_{0}}^{\frac{5}{3}}{{D}^{\frac{1}{3}}}}, $

(15)

其中，r₀为大气相干长度；$ k=\frac{2\pi }{\lambda } $；λ为激光波长。

4 综合考虑两随机作用源时的激光测距方程推导

漫反射目标相对于光束中心的偏差距离是望远镜跟踪抖动与大气湍流共同作用的结果，且这两个作用相互独立，根据概率论，两个物理过程对同一参数的作用可表示成两个函数的卷积^[5-6]，即

$ {{g}_{\text{total}}}({{{\vec{\rho }}}_{\text{total}}};0,{{\sum }_{\text{total}}})={{g}_{\text{t}}}\otimes {{g}_{\text{a}}}. $

(16)

具体形式可表示为

$ {{g}_{\text{total}}}({{{\vec{\rho }}}_{\text{total}}};0,{{\sum }_{\text{total}}})=\frac{1}{2\pi {{\left| {{\sum }_{\text{total}}} \right|}^{\frac{1}{2}}}}~{{e}^{-\frac{1}{2}}}^{{{({{{\vec{\rho }}}_{\text{total}}})}^{\text{T}}}{{\sum }_{\text{total}}}^{-1}({{{\vec{\rho }}}_{\text{total}}})}, $

(17)

其中，∑_total可表示为

$ {{\sum }_{\text{total}}}={{\sum }_{12}}+{{\sum }_{2}}=\left( \begin{matrix} \sigma _{{{x}_{1}}}^{2}{{R}^{2}}+\sigma _{{{x}_{2}}}^{2} & 0 \\ 0 & \sigma _{{{y}_{1}}}^{2}{{R}^{2}}+\sigma _{{{y}_{2}}}^{2} \\ \end{matrix} \right)=\left( \begin{matrix} \sigma _{xt}^{2} & 0 \\ 0 & \sigma _{yt}^{2} \\ \end{matrix} \right), $

(18)

其中，$ {{{\vec{\rho }}}_{\text{total}}} $为综合考虑两个作用元时，漫反射目标相对于光斑中心的距离偏差；T为转置运算符。

根据$ E\left( \rho \right)={{\frac{{{E}_{0}}}{\pi {{\rho }_{\text{e}}}^{2}}}^{-\frac{{{\rho }^{2}}}{{{\rho }_{e}}^{2}}}} $，能够求出在两个随机作用源共同作用时，激光在传输至z处的能量均值E：

$ \begin{align} & \bar{E}=\iint{\frac{{{E}_{0}}}{\pi {{\rho }_{\text{e}}}^{2}}{{e}^{-\frac{{{\rho }_{\text{total}}}^{2}}{{{\rho }_{\text{e}}}^{2}}}}{{g}_{\text{total}}}({{{\vec{\rho }}}_{\text{total}}};0,{{\sum }_{\text{total}}})}\text{d}x\text{d}y \\ & =\frac{{{E}_{0}}}{\pi {{\left| {{\sum }_{\text{total}}} \right|}^{\frac{1}{2}}}\sqrt{\left( \frac{{{\rho }_{\text{e}}}^{2}}{\sigma _{xt}^{2}} \right)+2}\sqrt{\left( \frac{{{\rho }_{\text{e}}}^{2}}{\sigma _{yt}^{2}} \right)+2}}. \\ \end{align} $

(19)

假设激光脉冲能量为E₀，激光发散角半角θ_e，漫反射目标距测站距离为R，在距离为R时的光斑面积为S_光，大气透过率T_e，测距系统激光发射光路光学透过率为T_r，h为普朗克常量；υ为光波频率；η为探测器的量子效率；T_r′为接收光路的光学透过率；a为大气衰减系数。被测目标为均匀漫反射体(反射光强度在2π立体角内各向同性)，有效反射面为S，反射率为ρ_r，当$ S\ll {{S}_{光}} $时，口径为D的望远镜接收光电子数n_s可表示为

$ {{n}_{\text{s}}}=\frac{\bar{E}S{{\rho }_{\text{r}}}{{T}_{\text{r}}}{{T}_{\text{r}}}^{\prime }{{T}_{\text{e}}}^{2}\eta \pi \frac{{{D}^{2}}}{4}}{2\pi {{R}^{2}}h\upsilon }, $

(20)

将E代入可得

$ {{n}_{\text{s}}}=\frac{{{E}_{0}}}{\pi |{{\sum }_{\text{total}}}{{|}^{\frac{1}{2}}}\sqrt{\left( \frac{{{\rho }_{\text{e}}}^{2}}{\sigma _{xt}^{2}} \right)+2}\sqrt{\left( \frac{{{\rho }_{\text{e}}}^{2}}{\sigma _{yt}^{2}} \right)+2}}\frac{S{{\rho }_{\text{r}}}{{T}_{\text{r}}}{{T}_{\text{r}}}^{\prime }{{T}_{\text{e}}}^{2}\eta \pi \frac{{{D}^{2}}}{4}}{2\pi {{R}^{2}}h\upsilon }, $

(21)

其中，ρ_e为光束传输距离为z时的光斑半径，可表示为

$ {{\rho }_{\text{e}}}=\frac{D}{2}+{{\theta }_{\text{e}}}R+{{\rho }_{\text{ae}}}, $

(22)

ρ_ae为大气湍流引起的光束扩展的均值，假设大气湍流引起的光束扩展的均值为0，将其代入方程中可得空间碎片漫反射激光测距方程：

$ \begin{align} & {{n}_{\text{s}}}=\frac{{{E}_{0}}}{\pi \sqrt{{{(D/2+{{\theta }_{\text{e}}}R)}^{2}}+2\sigma _{xt}^{2}}\sqrt{{{(D/2+{{\theta }_{\text{e}}}R)}^{2}}+2\sigma _{yt}^{2}}} \frac{S{{\rho }_{\text{r}}}{{T}_{\text{r}}}{{T}_{\text{r}}}^{\prime }{{T}_{\text{e}}}^{2}\eta \pi \frac{{{D}^{2}}}{4}}{2\pi {{R}^{2}}h\upsilon }a, \\ \end{align} $

(23)

5 数值模拟计算分析 5.1 望远镜跟踪精度对不同激光发散角测距时的回波强度影响

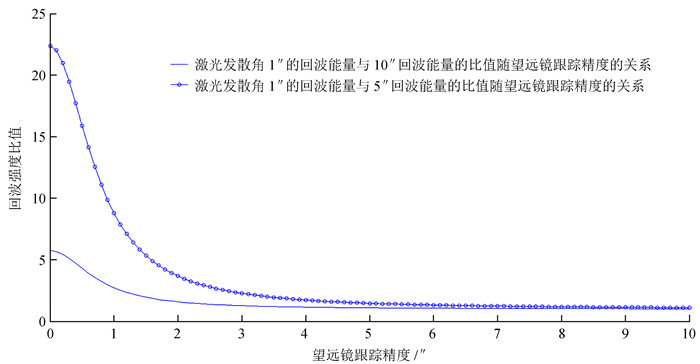
图 2显示了在忽略大气湍流对光束的作用时，望远镜口径为1.05 m，目标距离为1 500 km，激光发散角为1″时的回波能量分别与激光发散角为5″、10″时回波能量的比值随望远镜跟踪精度的关系。如图，当望远镜跟踪精度小于1″时，采用高倍率的激光发射扩束系统以减小激光发散角，对提高回波强度的作用非常明显。而随着望远镜跟踪性能的下降，减小激光发散角并不能提高望远镜接收的回波强度。

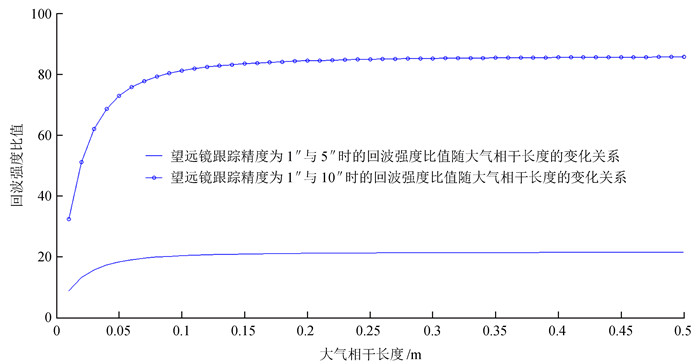
在不同大气相干长度条件下，激光发散角为1″时，望远镜跟踪精度对回波强度的影响。图 3显示了在激光发散角为1″，望远镜跟踪精度为1″与跟踪精度为5″、10″所接收的回波能量比值随大气相干长度的变化关系。由图，在不同跟踪精度下的回波能量比值随大气相干长度的增加而提高，在大气相干长度为1 cm时，跟踪精度为1″与10″所接收的回波能量比值约为30，而当大气相干长度为10 cm时，1″跟踪精度的回波强度比跟踪精度为10″时提高了近80倍。

5.2 大气湍流强度对不同激光发散角测距时的回波强度影响

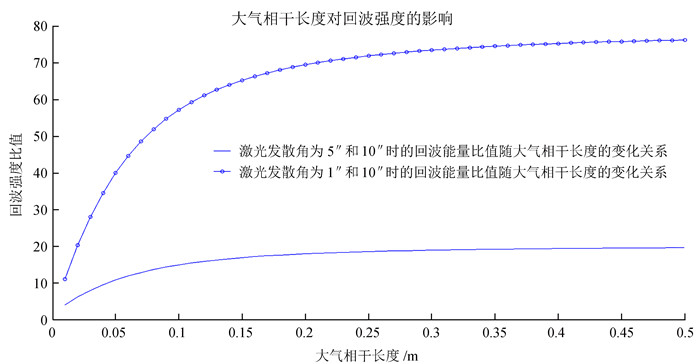
图 4显示了在忽略大气湍流作用的条件下，激光发散角为1″时的回波强度分别与发散角为5″、10″时的回波强度比值随大气相干长度的变化。由图，在大气相干长度为1 cm时，激光发散角为1″时的回波强度与发散角为10″时的回波强度的比值约为10。随着大气相干长度的增加，比值也随之提高，在大气相干长度为10 cm时，二者比值约为55，而且随着大气相干长度的增加回波强度还有一定的提升空间。

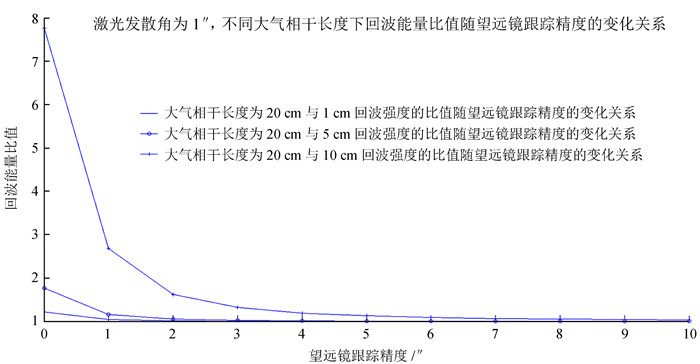
在不同望远镜跟踪精度的条件下，激光发散角为1″时，大气相干长度对回波强度的影响。图 5显示了激光发散角为1″时，大气相干长度为20 cm的回波能量与相干长度分别为1 cm、5 cm和10 cm时，回波强度的比值随望远镜跟踪精度的关系。如图，在望远镜跟踪精度为1″时，20 cm与1 cm的大气相干长度所对应的回波强度比值为2.8，随着望远镜跟踪精度的降低，大气湍流强度的改善并不能有效提高回波强度，在同样的跟踪精度下，大气相干长度从5 cm、10 cm分别提高到20 cm后，回波强度分别提高了1.2和1.1倍。

6 总结

激光测距系统的回波强度受激光发散角、望远镜跟踪精度与大气湍流强度共同作用的影响。对低轨的目标进行测距时，当站址处的大气相干长度不小于10 cm时，大气湍流造成的光斑抖动对测距系统探测性能的影响不明显；在保证望远镜跟踪精度的前提下，减少激光发散角能够大幅提高测距系统的探测性能，然而在激光器光束质量确定后，减少激光发散角需增加望远镜口径，提高大口径望远镜的跟踪精度对伺服控制系统及驱动系统提出更高要求。在现有的技术条件下，利用测距系统成像终端对目标进行闭环跟踪，通过实时控制高速压电摆镜以修正激光发射方向，采用这种方式来减小望远镜跟踪精度对测距系统性能的影响。