2. 中国科学院月球与深空探测重点实验室, 北京 100012
2. Key Laboratory of Lunar and Deep Space Exploration, Chinese Academy of Sciences, Beijing 100012, China
深空探测以及射电天文的高速发展 ,对地基接收天线提出了越来越高的要求 。相对于单个大口径天线,组阵天线具有接收性能优良、工作状态稳定、建造费用低、灵活性强等优势,并且可以带动多个交叉学科的发展[1]。1990年美国的一项重要研究表明:中等大小(25 m至40 m)的天线阵要比单个大口径天线各项性能更加优良。70 m天线和34 m天线阵能使数据接收能力提高25%以上[2]。
美国是较早应用天线阵进行深空探测的国家。美国国家航空航天局(National Aeronautics and Space Administration,NASA)的旅行者2号探测器在20世纪80年代抵达天王星时,依靠位于澳大利亚堪培拉70 m天线与180 km以外的64 m天线的天线阵进行数据接收;抵达更远的海王星时,用来接收数据的天线阵包括格尔德斯顿的70 m天线和两个34 m天线,以及位于美国新墨西哥州的超大规模阵列的27个25 m口径天线[3]。
目前,正在建设和计划建设的天线阵主要有平方千米阵列(Square Kilometre Array,SKA)、阿伦望远镜、美国深空探测网(Deep Space Network,DSN)等。我国的深空天线阵技术研究尚处于起步阶段,分别在国家天文台密云站建立了4天线Ku频段实验系统,在北京怀柔站建立了4天线S/X频段实验系统①,[4],并针对嫦娥2号、同步卫星等进行了组阵实验。
http://npd.nsfc.gov.cn/projectDetail!showPDF.action?code=10903016&pid=2012-12-31
天线阵应用于深空探测需要克服两个问题。首先是单天线接收信号的低信噪比,火星探测器的路径衰减要比地球同步卫星高63~80 dB[5];其次是深空探测的实时性要求,使得天线阵必须缩短相关时间。
当探测器信号非常微弱时,为达到足够的信噪比,在相关时需要很长的积分时间;而由于地球对流层大气的扰动造成各天线信号的相位波动,导致天线信号间长时间相关性变差,从而严重影响信号的合成性能[6]。传统的相位差估计算法包括SIMPLE、SUMPLE[7]、EIGEN[8]和LSFIT[9]等。由于大气相位扰动对相关时间的限制,在接收低信噪比信号时,相关算法难以实现相位差的正确估计。文[10]根据甚大天线阵(Very Large Array,VLA)在9月的观测数据,给出了由于大气相位扰动导致的合成效率下降示意图,如图 1,在Ka频段(34 GHz)合成损失达到83%(-7.7 dB)。为了提高信号相位差估计的精度,提高微弱信号合成的性能,有必要对大气相位扰动进行实时修正。
由大气层引起的信号相位扰动的修正是目前国内外的研究热点。文[11]使用天线阵对低亮度天体NGC4261(3C270)进行观测时,接收信号的相位误差主要来自大气层相位扰动、信号源频移、接收天线地理位置误差、设备误差等。实验表明,大气层相位扰动是相位误差的重要来源,需要通过多种技术进行有效的修正。
1 大气相位延迟的组成及特点大气层对于电磁波的延迟作用主要表现在两方面:(1)电磁波穿过大气层时,传播速度不再等于光速,实际传播速度与传输路径上各处的大气折射率有关,因此这一部分的延迟可以通过大气折射率表示;(2)由于大气层折射率的不均匀,电磁波在大气层中的传播路径会发生弯曲,但是当信号源高度角不是很低时,路径延迟要远小于因波速改变造成的延迟[12]。因此,本文重点讨论因波速改变造成的延迟。
大气层由电离层和对流层两个基本部分组成。由于电离层与对流层的组成、时空变化具有很大差异,因此对电磁波的延迟作用也有很大不同。
电离层主要集中在距地面50~1 000 km的高度。由于直接与外太空接触,电离层中大气分子受太阳风以及宇宙射线辐射发生电离,使得电离层中充满了大量的自由电子和正离子。 对流层主要集中在距地面50 km以下的区域。由于高度相对较低,远离外太空辐射,对流层中的带电粒子比较少。对流层集中了整个大气层99%以上的质量,其中包含的成分比较复杂,不仅有呈气态的各种气体分子,还有水蒸气冷凝成的液态雨滴,以及固态的冰晶和近地面的灰尘沙粒等等。此外,由于靠近地表热源,近地大气层具有显著的对流作用。组成成分的复杂以及对流作用的存在,使得对流层延迟随时间、空间的变化相对于电离层延迟更加显著。
1.1 电离层相位扰动原理分析由于大量带电粒子的存在,电离层是一种色散介质。色散介质中,电磁波的折射率与电磁波的频率有关,这就使得不同频率电磁波组成的波群通过电离层时会发生色散,相速超过群速[13]。文[14]通过对经典的电离层电磁波折射率公式进行简化,使用泰勒公式对经典公式展开,并忽略对结果影响不大的高阶项,给出了相位折射率和群折射率引起的延迟的近似公式:
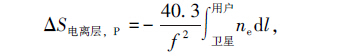
|
(1) |
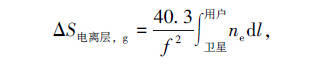
|
(2) |
其中, ne为电磁波传播路径上的电子密度; f 为电磁波频率。
除此以外,在低纬度和高纬度地区,会发生电离层闪烁的现象。电离层闪烁一般源于太阳上剧烈的能量和物质喷发以及一定条件下大气层中出现的非线性不稳定变化。电离层闪烁对空间飞行器的影响非常大,有时会导致地面天线与空间飞行器暂时失联。文[15]使用多颗全球定位系统卫星对海口市2003年、2004年的两次电离层闪烁现象进行了观测以及分析,分析得到的数据将为建立我国低纬度地区电离层闪烁模型提供依据。
1.2 对流层相位扰动原理分析对于15 GHz频率以下的电磁波,对流层是一种非色散介质[16]。对流层延迟主要由两部分组成。一部分是由干燥空气引起的,它引起了90%的对流层延迟,这种延迟一般被称作干延迟,天顶方向的干延迟约为2 m[17]。干延迟随时间、空间的变化都比较缓慢。对流层延迟的另一部分是由湿空气引起的,
被称作湿延迟。湿延迟主要分布在10 km以下的大气中。相对于干延迟,湿延迟在对流层总延迟中只占不到10%,天顶方向的湿延迟约为0~40 cm[17]。但是由于湿空气分布以及变化的随机性,湿延迟随时间和空间的变化都比较剧烈,预测难度也要高于干延迟。
对流层延迟可以认为是电磁波穿过真空(理想)与穿过对流层(实际)的时间差,文[18]通过计算时间差,并基于对流层折射率的变化性,得到对流层延迟与大气层折射指数 N 的关系:
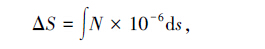
|
(3) |
其中,ds 为接收站与信号源的视线距离积分; N 为大气折射指数,与电磁波穿过大气层各处的大气状态有关[19]:

|
(4) |
其中, Pd、 Pw分别为干空气、湿空气分压; T 为大气温度; k1、 k2、 k3为经验常数。
除了干空气和湿空气造成的延迟以外,空气中的沙尘雾霾也会对电磁波相位造成干扰。文[20]指出,当空气中的沙尘密度为40~60 g/m3(沙尘暴时的沙尘密度)时,电磁波延迟可达到4~5 m,沙尘的折射率 N s≈18。基于我国北方部分地区多风沙、多雾霾的气候特点,雾霾沙尘相位干扰的研究成为一个具有很大应用价值的方向。
在大气相位延迟中,电离层延迟占大部分,天顶方向电离层延迟可达到15 m左右,对流层的天顶延迟相对较小,为2.5 m左右。但是,由于对流层的不稳定性,使得对流层延迟可以在很短的时间、很小的区域内发生变化,而电离层延迟的空间相关性更强,已有研究表明宁静情况下中纬地区电离层空间相关距离在同一纬度方向上可达上千千米,而沿同一经度方向也达数百千米[21]。对于基线长度在几千米以内的阵列天线而言,对流层延迟对天线之间相位误差的影响要远大于电离层延迟。除此以外,采用双频接收机配合其它电离层延迟模型,对电离层延迟预测的准确率可以达到90%以上,而对流层延迟的预测准确率一般不足70%,湿延迟的预测准确率更是不到30%。基于对流层延迟预测的难度以及对深空阵的影响,后文着重讨论对流层延迟的修正技术。
2 国内外对流层延迟模型研究由上一节对流层延迟原理的讨论可知,对流层延迟是由传播路径上的大气层温度、气压等气象参数决定的。不可能对电磁波传播路径上各点的大气参数进行实测,但是可以使用地表温度、气压以及海拔高度表示传播路径上各个点的大气参数。将地表大气参数作为输入,对流层延迟作为输出,进行建模,然后直接或间接测量对流层延迟,对模型进行反复验证、修改。这种技术思路是目前比较常用的一种获得对流层延迟的方法。这类模型应用比较多,有Saastamoinen模型、Hopfield模型、Egnos模型、Black模型等等。
文[22]使用了ALGO观测站连续30 d的全球定位系统观测数据作为参考值,对Saastamoinen模型、Hopfield模型、Black模型和Egnos模型的预测精度进行校验。实验选取一个月内9 000个时间点作为采样点,在每个采样点测量3种模型所需的气象数据。结果表明,前3种模型在天顶方向的修正精度较高,采样点最大误差不超过10 cm;Egnos模型由于不需要很多实测量,应用范围更广,但精度要比前3个模型低。
除了传统模型,国内外学者通过改变参数选择、改进模型算法,提出了诸多新的对流层延迟模型。
新不伦瑞克大学提出了UNB3模型[23],其最大的特点是不需要气象传感器对地面气象参数进行实时测量。模型首先给出了一个基于经纬度和季节的气象参数经验表,该表是经过长时间测量多地气象参数预先总结的。使用者通过内插得到本地本时刻的气象参数近似值,代入模型进行延迟估计。
文[24]研究了对流层干湿延迟与经纬度、高程、季节、时刻的关系,引入全球定位系统导航中常用的多曲面方程,建立了一种区域对流层干湿延迟模型。经过与全球定位系统测量结果的观测对比,这种模型对干延迟的修正性能要好于UNB3模型,湿延迟修正效果则比较差。
文[25]将全球定位系统观测网中的每个观测站视为神经元,采用反向传播(Back Propagation,BP)神经网络预测对流层延迟,并与全球定位系统的观测值进行对比分析,对比的结果显示:76%的预测值与实际值之间的偏差在 3 cm以内。利用反向传播神经网络进行预测对流层延迟的精度达到厘米级,36.84%的站点达到毫米级。
基于以上的讨论可知,目前的几种对流层延迟模型以及改进模型对干延迟的预测精度较高。但是,延迟模型仍旧具有很大的局限性,其中限制了延迟模型应用于阵列天线的最大问题是模型对湿延迟的预测精度不足。
文[26]使用北京、武汉、拉萨近一个月的全球定位系统接收数据作为参考,对Saastamoinen模型和Hopfield模型预测对流层湿延迟的精度进行了研究,得出了天顶湿延迟模型的准确率只有20%~30%的结论。
为了分析干延迟和湿延迟对天线阵的影响,文[27]对相邻天线的延迟变化相关性进行观测实验。实验观测了甚大阵天线中,两个间隔360 m的天线W18和W16在20 min内的相位相关性。实验结果显示:对流层相位延迟的长时间大区域变化(主要由干延迟变化引起)是部分相关的,而短时间小区域变化(主要由湿延迟变化引起)是不相关的。因此,对于基线长度在几千米内的天线阵,天线之间的相位差主要是湿延迟造成的。
综上所述,对流层延迟模型可以用来修正整个天线阵的对流层干延迟,而对于湿延迟造成的天线之间的相位差,使用模型修正的效果则比较差。基于延迟模型对湿延迟预测精度的不足,还需要引进其他技术修正对流层延迟。
3 深空探测天线阵相位修正技术由于深空探测对于实时性的要求,常用于射电天文天线阵的 “快速偏开” 相位修正技术,在深空探测中无法使用。“快速偏开” 技术的基本原理是选择与目标源相邻的参考源,观测天线在目标源和参考源之间交替切换,对两次参考源的相位延迟进行内插,得到对准目标源时刻的相位延迟。由于这一修正技术,接收天线无法保持对探测器的连续跟踪,所以这种技术不能完全应用于深空探测中,但是其观测参考源纠正目标源的思路在深空探测中是可以借鉴的。
此外,天线阵列信号合成时,更多关注天线之间的相位差。即使每个天线的绝对延迟值无法精确测量,只要天线之间的相位差准确,即可实现高效的信号合成。这也就意味着差分的思想在修正天线阵相位延迟中使用比较多。
3.1 基于全球定位系统技术的相位修正全球定位系统接收机测量对流层延迟的基本原理是在已知卫星精密星历的前提下,计算卫星与接收站的实际距离,再使用全球定位系统接收机接收信号,计算全球定位系统卫星与接收站的测量距离,两者的差值即为总的大气层延迟。除了应用于深空探测,通过全球定位系统测得的大气延迟还经常用于反演对流层中的水汽含量,因此反演得到的水汽含量的准确度,可以间接地表示测量大气延迟的准确度。
全球定位系统测量大气层延迟的一个主要问题是全球定位系统卫星与接收机的时钟偏差。目前消除时钟偏差的常用方法是采用双全球定位系统接收机差分。文[28]使用了全球定位系统接收机测量大气相位延迟,并且反演对流层水汽含量。在实验中对单个高精度全球定位系统和双全球定位系统接收机差分的效果进行了对比研究,结论是采用双全球定位系统接收机差分得到反演结果的误差均方值只有单个接收机的一半。
采用差分全球定位系统测量大气层延迟的技术已经被整合成各种软件包,使用最广泛的是GAMIT软件。文[17]使用GAMIT与国际全球定位系统服务组织公布的天顶对流层延迟产品(IGS ZPD)进行对比测试,两种软件得到的结果非常接近,日平均误差接近0。
基于全球定位系统技术修正大气相位的缺点是计算结果实时性较差。由于对流层中湿空气变化迅速,使得全球定位系统测量技术需要更长的相关时间和更多的采样数据来计算准确的延迟结果,这就限制了全球定位系统测量技术在深空探测中的应用。使用全球定位系统测量对流层延迟,达到厘米级精度需要一个小时的计算时间,要达到毫米级及更高的精度,会有12 h的计算延迟[29]。
3.2 基于微波辐射计、激光发生器的相位修正地基的微波辐射计主要是利用大气层在22~200 GHz频带内辐射特性对大气层部分参数进行测量。通过测量氧气在60 GHz处的亮温度可以得出大气温度分布;测量22 GHz(湿润地区)和183 GHz(干燥地区)水汽谐振带水汽线压力增宽的辐射强度和形状,可以计算大气层水汽轮廓线;另外还可以通过测量光谱的形式测量云液态水廓线的分辨率。
利用微波辐射计测量对流层延迟的一种方法是使用单台辐射计测量大气层水汽廓线,通过水汽廓线的亮温度计算对流层延迟。文[30]使用微波辐射计测量了多个频率下的水汽廓线亮温度,并分析了亮温度与对流层延迟的关系。文章认为,对流层延迟不仅与亮温度有关,还与大气层的气压、温度、电磁波的频率有关。当接收信号的频率取特定值时,对流层延迟与水汽廓线的亮温度成正比。文[31]使用微波辐射计对空间成像进行校正,结果表明在22 GHz时的纠正效果比较满意。
另一种计算对流层延迟的方法是采用两台微波辐射计测量对流层延迟的结果进行差分,差分得到的结果要比单台微波辐射计得到的结果误差更低。文[32]将两台微波辐射计测量对流层延迟差分的结果,与两台基线长度为250 m的阵列天线的差分结果进行了对比,对比结果显示两者的数值非常接近。实验中,微波辐射计差分与天线差分之间的误差主要由微波辐射计计算干延迟精度不足造成的。 激光发生器测量对流层延迟的精度比微波辐射计更高。激光发生器测量的基本原理与微波辐射计类似,也是通过测量对流层亮温度计算延迟。不同的是,使用微波辐射计时,辐射源来自太阳光,而使用激光发生器时,辐射源来自地面的激光发生器。与微波辐射计测量法相比较,使用激光发生器测量到的延迟结果精度更高。文[33]对比分析了大气温度对微波辐射计测量结果和激光辐射计测量结果的影响,结果表明大气温度的波动会对微波辐射计的测量结果造成最大10 mm的误差,而激光发生器的误差只有2~3 mm。激光发生器测量对流层延迟的最大问题是辐射源功率太低,这就需要更长的观测时间或者更大型的天线来测量对流层的亮温度。
对比微波辐射计测量对流层延迟与全球定位系统测量延迟,微波辐射计的优势在于不依赖参考卫星,不受参考卫星误差的影响,而且可以实时地反馈延迟信息,而全球定位系统计算大气层延迟会有一段时间的延迟。微波辐射计测量延迟的不足表现在:微波辐射计价格昂贵;测量干延迟的结果不精确;微波辐射计在降雨天气下无法使用。
3.3 基于校准天线的相位修正这种方法的原理是在整个天线阵中抽出部分天线作为校准天线。校准天线通过观测校准源测量大气层延迟,再通过内插等方法得到观测天线的大气层延迟。
该修正方法的一个问题是校准源与目标源的频率比值与它们的延迟比值的关系。文[34]利用甚长基线阵列天线(Very Long Baseline Array,VLBA)对频率14.375 GHz和43.125 GHz的两组信号源进行了10 min的观测。观测结果如图 2[34]。图 2中包含了两个观测站的观测数据,可以认为两组信号源的相位延迟相关性比较大。
文[35]使用地球同步卫星(发射频率19.45 GHz)作为校准源,3C279天体(发射频率146.81 GHz)作为目标源,使用日本冈山毫米波阵列验证校准天线修正技术的有效性。实验的结果显示,在去除了因校准天线和观测天线方位角不同造成的误差后,修正的均方根误差为0.06 mm。
与基于全球定位系统、微波辐射计的修正方法相比,采用校准天线的最大优势是在保证较高修正精度的前提下,可以不间断、低延迟地工作,且不受天气的影响;而缺点主要表现在:(1)抽出部分天线作为校准天线,这种方法降低了整个天线阵的性能;(2)用来校准的参考源必须与目标源位置相近,且不会发生频移,选择符合要求的校准源比较困难;(3)校准源与目标源的位置不一致,导致了电磁波穿过大气层的路径不一致,使得测得的延迟出现偏差。另外受到天线阵几何排列的影响,不是所有的阵列都适合抽出校准天线进行修正。
4 总结及展望在介绍大气层延迟原理的基础上,将常用的几种对流层延迟模型及其改进做了论述,并且基于延迟模型预测湿延迟不足的缺点,介绍了几种用于深空探测中天线阵的相位修正技术。
在正常气象条件下,大部分常用的对流层延迟模型均方差精度可以达到10 cm以下,改进模型的精度则更高。但是,无论是基于模型修正大气相位延迟,还是基于全球定位技术、微波辐射计、校准天线修正延迟,在深空阵的应用中都存在着亟待解决问题。
常用延迟模型中的经验参数是根据全球或者欧美地区的大气环境推导得到的,延迟模型在中国地区使用,会导致模型误差因为地理位置的差异而增大。对延迟模型进行改进,推导适合中国地区使用的模型经验参数,是提高延迟模型精度的有效途径。
因为各自优缺点的存在,单独使用全球定位系统、微波辐射计、校准天线对大气延迟进行测量修正都无法完全满足深空探测的要求。将多种修正技术综合使用成为深空探测相位修正的必然趋势。在保证综合修正技术性能的前提下,尽量降低设备的建造成本是一项非常有意义的研究工作。
此外,随着宇航技术的发展,Ku、Ka等高频段信号的应用越来越广。对于频率大于15 GHz的电磁波,对流层不再是一种单纯的色散介质。目前国内外将对流层作为一种色散介质进行的研究非常匮乏,加强这方面的研究成为一种必然。
随着我国深空探测事业的迅猛发展,更多性能优异的天线阵列的建设势在必行。高精度大气相位扰动修正技术是深空阵发挥优势必不可少的部分。
| [1] | Rogstad D H, Mileant A, Pham T T. 深空网的天线组阵技术[M]. 李海涛, 译. 北京:清华大学出版社, 2005. |
| [2] | 孙志远, 乔彦峰. 美国深空跟踪通信系统的现状及发展趋势[C]//中国宇航学会飞行器测控专业委员会2005年航天测控技术研讨会. 2005. |
| [3] | 李海涛, 李宇华, 匡乃雪. 深空探测中的天线组阵技术[J]. 飞行测控学报 , 2004 , 23 (4) : 57 –60 Li Haitao, Li Yuhua, Kuang NaiXue. The array antenna group in the detection of deep space technology[J]. Journal of Flight Measurement and Control , 2004 , 23 (4) : 57 –60. |
| [4] | 洪家财. 天线组阵试验系统顺利建成并投入应用[J]. 装备指挥技术学院学报 , 2011 , 22 (5) |
| [5] | 朱新颖, 李春来, 张洪波. 深空探测VLBI技术综述及我国的现状和发展[J]. 宇航学报 , 2010 , 31 (8) : 1893 –1899 Zhu Xinying, Li Chunlai, Zhang Hongbo. A survey of VLBI technique for deep space exploration and trend in China current situation and development[J]. Journal of Astronautics , 2010 , 31 (8) : 1893 –1899. |
| [6] | Nessel J A, Acosta R J. Directivity of a sparse array in the presence of atmospheric-induced phase fluctuations for deep space communications[EB/OL]. 2010[2016-02-10]. http://permanent.Access.Gpo.gov/gpo802/TM-2010-216241.pdf. |
| [7] | Rogstad D H. The SUMPLE algorithm for aligning arrays of receiving radio antennas:coherence achieved with less hardware and lower combining loss[R]//IPN Progress Report. 2005:42-162. |
| [8] | Cheung K M. Eigen theory for optimal signal combining:a unified approach[R]//The Telecommunications and Data Acquisition Progress Report. 1996:1-9. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.495.7032 |
| [9] | Vilnrotter V A, Rodemich E R, Dolinar S J. Real-time combining of residual carrier array signals using ML weight estimates[J]. IEEE Transactions on Communications , 1992 , 40 (3) : 604 –615. DOI: 10.1109/26.135731 |
| [10] | D'Addario L R. Estimates of atmosphere-induced gain loss for the Deep Space Network Array[R]//The Interplanetary Network Progress Report. 2005:1-7. http://cn.bing.com/academic/profile?id=110570073&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | Middelberg E, Roy A L, Walker R C, et al. VLBI observations of weak sources using fast frequency switching[J]. Astronomy&Astrophysics , 2005 , 433 (3) : 897 –910. |
| [12] | 刘基余. GPS卫星导航定位原理与方法[M]. 北京: 科学出版社. 2008. |
| [13] | 肖志斌, 刘瀛翔, 唐小妹, 等. 电离层色散特性对导航信号接收的影响[J]. 国防科技大学学报 , 2014 (3) : 146 –149 Xiao Zhibin, Liu Yingxiang, Tang Xiaomei, et al. Effect of ionosphere dispersion on the navigation signal receiving[J]. Journal of National University of Defense Technology , 2014 (3) : 146 –149. |
| [14] | 徐冬. 大气层对卫星导航信号的时延影响及修正[J]. 电讯技术 , 2006 , 46 (4) : 132 –136 Xu Dong. Effect of atmosphere on satellite navigation signal delay and correction method[J]. Telecommunication Technique , 2006 , 46 (4) : 132 –136. |
| [15] | 陈丽, 冯健, 甄卫民. 利用GPS进行电离层闪烁研究[J]. 全球定位系统 , 2006 , 31 (5) : 9 –12 Chen Li, Feng Jian, Zhen Weimin. The study of ionospheric scintillation by using GPS signals[J]. GNSS World of China , 2006 , 31 (5) : 9 –12. |
| [16] | Hofmann-Wellenhof B, Lichtenegger H, Collins J. Global Positioning System:theory and practice[M]. Vienna: Springer Vienna. 1992. |
| [17] | 何战科. 卫星测定轨中两种对流层延迟估算方法的比较[C]//全国测控计量仪器仪表学术年会. 2009. |
| [18] | 李成才, 毛节泰. 地基GPS遥感大气水汽总量中的静力延迟和湿延迟[J]. 大气科学 , 2004 , 28 (5) : 795 –800 Li Chengcai, Mao Jietai. The concepts of hydrostatic delay and wet delay in remote sensing water vapor with ground based GPS receivers[J]. Chinese Journal of Atmospheric Sciences , 2004 , 28 (5) : 795 –800. |
| [19] | Spilker J J. GPS signal structure and performance characteristic[J]. Navigation , 1978 , 25 (2) : 121 –146. DOI: 10.1002/navi.1978.25.issue-2 |
| [20] | Solheim F S, Vivekanandan J, Ware R H, et al. Propagation delays induced in GPS signals by dry air, water vapor, hydrometers, and other particulates[J]. Journal of Geophysical Research , 1999 , 104 (D8) : 9663 –9670. DOI: 10.1029/1999JD900095 |
| [21] | 邓忠新, 甄卫民, 刘瑞源, 等. 强磁暴期间低纬电离层空间相关性及其预报应用初步分析[C]//中国地球物理学年会. 2008. http://cpfd.cnki.com.cn/article/cpfdtotal-zgdw200810001502.htm |
| [22] | 王新龙, 李亚峰. GPS定位中4种对流层延迟修正模型适应性分析[J]. 电光与控制 , 2008 , 15 (11) : 5 –9 Wang Xinlong, Li Yafeng. Applicability analysis of four troposphere delay error models in GPS positioning[J]. Electronics Optics&Control , 2008 , 15 (11) : 5 –9. |
| [23] | Elliot D Kaplan, Christopher J Hegarty. GPS原理与应用[M]. 寇艳红, 译. 北京:电子工业出版社, 2007. |
| [24] | 戴吾蛟, 赵岩. 区域对流层干湿延迟建模[J]. 大地测量与地球动力学 , 2013 , 33 (2) : 72 –76 Dai Wujiao, Zhao Yan. Modeling the dry and wet component of regional tropospheric delay[J]. Journal of Geodesy and Geodynamics , 2013 , 33 (2) : 72 –76. |
| [25] | 王勇, 张立辉, 杨晶. 基于BP神经网络的对流层延迟预测研究[J]. 大地测量与地球动力学 , 2011 , 31 (3) : 134 –137 Wang Yong, Zhang Lihui, Yang Jing. Study on prediction of zenith tropospheric delay by use of BP neural network[J]. Journal of Geodesy and Geodynamics , 2011 , 31 (3) : 134 –137. |
| [26] | 曲建光, 赵丽萍, 刘基余. 利用GPS数据来评定Saastamoinen和Hopfield天顶湿延迟模型的精度[J]. 黑龙江工程学院学报 , 2006 , 20 (1) : 1 –5 Qu Jianguang, Zhao Liping, Liu Jiyu. Assessing the precision of Saastamoinen and Hopfield zenith wet delay model using GPS data[J]. Journal of Heilongjiang Institute of Technology , 2006 , 20 (1) : 1 –5. |
| [27] | Carilli C L. Tropospheric phase calibration in millimeter interferometry[J]. Radio Science , 1999 , 34 (4) : 817 –840. DOI: 10.1029/1999RS900048 |
| [28] | Braun J, Rocken C, Ware R. Validation of line-of-sight water vapor measurements with GPS[J]. Radio Science , 2001 , 36 (3) : 459 –472. DOI: 10.1029/2000RS002353 |
| [29] | Bar-Sever Y E, Jacobs C S, Keihm S, et al. Atmospheric media calibration for the Deep Space Network[J]. Proceedings of the IEEE , 2007 , 95 (11) : 2180 –2192. DOI: 10.1109/JPROC.2007.905181 |
| [30] | Sutton E C, Hueckstaedt R M. Radiometric monitoring of atmospheric water vapor as it pertains to phase correction in millimeter interferometry[J]. Astronomy&Astrophysics Supplement , 1996 , 119 (3) : 559 –567. |
| [31] | Marvel K B, Woody D P. Phase correction at millimeter wavelengths using observations of water vapor at 22GHz[C]//Proceedings of SPIE. 1998:442-452. http://cn.bing.com/academic/profile?id=2165202711&encoded=0&v=paper_preview&mkt=zh-cn |
| [32] | Morabito D D, D'Addario L R, Keihm S, et al. Comparison of dual water vapor radiometer differenced path delay fluctuations and site test interferometer phase delay fluctuations over a shared 250-meter baseline[R]//IPN Progress Report. 2012. |
| [33] | Bock O, Tarniewicz J, Thorn C, et al. Study of external path delay correction techniques for high accuracy height determination with GPS[J]. Physics&Chemistry of the Earth , 2001 , 26 (1) : 165 –171. |
| [34] | Middelberg E, Roy A L, Walker R C, et al. VLBI observations of weak sources using fast frequency switching[J]. Astronomy&Astrophysics , 2005 , 433 (3) : 897 –910. |
| [35] | Asaki Y, Shibata K M, Kawabe R, et al. Phase compensation experiments with the paired antennas method:2. millimeter-wave fringe correction using centimeter-wave reference[J]. Radio Science , 1996 , 31 (6) : 1615 –1625. DOI: 10.1029/96RS02629 |





