2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是中国自主研制、独立运行的全球卫星导航系统,致力于向全球用户提供高质量的定位、导航、授时服务[1]。北斗于2012年12月27日宣布对亚太大部分地区正式投入运行。美国的全球定位系统(Global Positioning System,GPS)于1995年对民用开放,各方面都比较成熟。比较两者的定位结果,不仅可以考察北斗系统的当前性能,也可以从性能差异评价两者的性能特点,对今后完善北斗系统、提高服务质量具有深刻的指导意义。近年来关于北斗和全球定位系统伪距单点定位性能的比较研究已有不少[2-5]。文[2]使用2011年8月25日在北京、上海、武汉、昆明采集的30 s采样间隔共24 h数据,得出北斗在伪距观测质量方面优于全球定位系统的结论;文[3]使用2012年11月6日在武汉采集的30 s采样间隔共24 h数据,得出北斗在伪距单点定位性能方面劣于全球定位系统的结论;文[4]利用2011年11月10日~12日3天在武汉采集的30 s采样间隔的数据,发现北斗和全球定位系统的定位精度相当,高程略差;文[5]利用2012年12月12日协调世界时3~9时在上海采集的北斗和全球定位系统数据,对两个系统的定位性能进行了比较研究,结论是北斗的定位结果明显差于全球定位系统。可见,在北斗系统建设的不同时期、不同地点、不同统计方法可能得出不同的性能比较结果。另外,实验条件、卫星运行状态和数据处理方法也可能对结果造成影响[6],而且随着北斗系统的进一步完善,其性能也会提高。所以,北斗和全球定位系统伪距单点定位结果的比较工作应在考虑更多的相关因素的条件下不断地进行下去。本文利用2014年4月底在北京采集的10 s采样间隔共56 h静态双频数据,对北斗和全球定位系统分别进行伪距单点定位解算,并从可见卫星数、位置精度因子、单位权中误差、水平面、高程等几方面详细分析比较了北斗和全球定位系统的定位结果。
1 定位性能指标伪距单点定位的精度主要由卫星几何分布和等效距离误差决定。位置精度因子反映某时刻可见卫星的几何分布[7],单位权中误差等效于卫星的测距误差。定位精度可表示为位置精度因子与单位权中误差的乘积[8]:
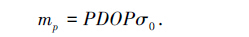
|
(1) |
PDOP 可由状态矩阵得到:
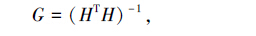
|
(2) |
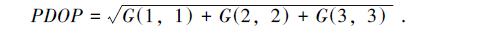
|
(3) |
位置精度因子的水平分量精度因子(Horizontal Dilution of Precision,HDOP)和垂直分量精度因子(Vertical Dilution of Precision,VDOP)分别反映某时刻可见星在水平和垂直方向的几何分布,钟差精度因子(Time Dilution of Precision,TDOP)反映接收机的性能:
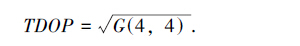
|
(4) |
单位权中误差可由残差矩阵得到[9]:
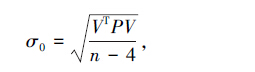
|
(5) |
其中, P 为权阵,等权观测时为单位阵; n 为可用卫星数。
内符合精度是系统多次测量对比的较差,反映了系统的稳定性[10]。内符合精度可表示为
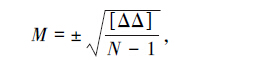
|
(6) |
其中, N 为测量次数;Δ为测量值与均值的差。 外符合精度是测量值与真值的较差,反映了系统的准确性[10]。外符合精度可表示为
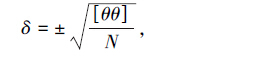
|
(7) |
其中, θ 为测量值与真值的差。
粗差反映了系统的可用性。统计学中由中心极限定理,大量的随机样本服从正态分布。对于服从正态分布的随机误差,在 (-3σ,+3σ) 的概率为99.7%。故可以认为误差绝对值大于3倍中误差的事件为不可能事件,这样的结果即为粗差[9]。
2 数据处理策略本文以和芯星通UR370-CORS双模接收机于协调世界时2014年4月28日2时至30日8时在位于北京的中国科学院国家天文台(40°0′10.444 0″ N,116°22′42.930 7″ E,59.436 1 m)接收到56 h双频伪距观测值。截止高度角均设为10°,采样率设为10 s,最终各得到19 384组数据。
观测期间北斗系统共有14颗卫星(5颗地球静止轨道(Geostationary Earth Orbit,GEO)卫星、5颗倾斜地球同步轨道(Inclined Geosynchronous Satellite Orbit,IGSO)卫星、4颗中高轨(Medium Earth Orbit,MEO)卫星)工作,其中13号中高轨卫星不可用(导航电文中卫星健康状态一直为1),故不采用该卫星的观测数据。另外,4月28日14时和15时(协调世界时)北斗5号地球静止轨道卫星也不可用,故在进行定位及结果分析时不使用5号卫星在该时段的数据。
北斗和全球定位系统数据处理策略相同,如表 1[10-12]。全球定位系统使用的WGS84坐标系和北斗使用的CGCS2000坐标系都是以地心为原点的空间直角坐标系,坐标轴定义相同,椭球参数中唯有扁率存在微小差异。由于伪距单点定位的精度在米级,故将全球定位系统和北斗的定位结果转换至大地坐标系中进行比较是可行的。在大地坐标系中可以证明,对米级精度的水平方向定位结果,无需考虑地球曲率可以在同一水平面上进行分析比较[13]。
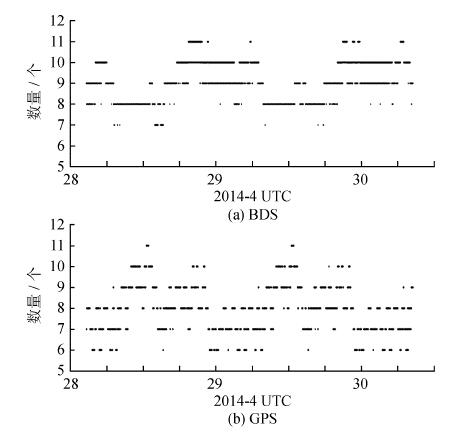
3 结果分析 3.1 可用卫星数图 1给出了观测期间北斗和全球定位系统的可用卫星数。北斗的可用卫星数多在8至10变化,平均值为9;全球定位系统的可用卫星数在6至10变化,平均值为8。北斗星座的卫星总数远少于全球定位系统,但可用卫星数多于全球定位系统,这是因为5颗地球静止轨道卫星在北京几乎全天可见,5颗倾斜地球同步轨道卫星可见时段也比中高轨卫星长。这与北斗系统在亚洲地区为增强系统这一设计是符合的[1]。
|
| 图 1 可用卫星数 Figure 1 The number of available satellites |
| 项目 | 处理方法 |
| 卫星位置 | 导航电文解算 |
| 卫星钟差 | 导航电文解算 |
| 对流层延迟 | Hopfield模型 |
| 电离层延迟 | 无电离层组合 |
| 定位算法 | 最小二乘法 |
| 加权方法 | 等权 |
通过比较可以发现,对于观测地点,观测时段在每天协调世界时0时左右北斗的可用卫星数达到最大,而此时全球定位系统的可用卫星数达到最小;在12时左右北斗达到最小,而全球定位系统达到最大。设想两系统组合使用,卫星数则可以恒定在较大值,这反映了北斗/全球定位系统组合导航的优越性[14]。
需要指出的是,某些时段中一个时刻对应有 “两个” 相邻的可用卫星数,这是由于某些卫星的观测值在当前时段时有时无造成的。以4月29日0时左右的观测为例,北斗5号地球静止轨道卫星的观测数据平均每半分钟就缺失一次,使得可用卫星数发生突变。卫星观测值的频繁缺失对应庞大的数据量,加上分辨率的限制使得看上去一个时刻对应有 “两个” 可用卫星数。卫星数出现跳跃较多的时段卫星数据连续性较差。可以看出北斗除在协调世界时0时左右卫星数据连续性较差,在其它时刻连续性较好;而全球定位系统全天卫星数据连续性一般,表现为可用卫星数频繁出现跳跃。
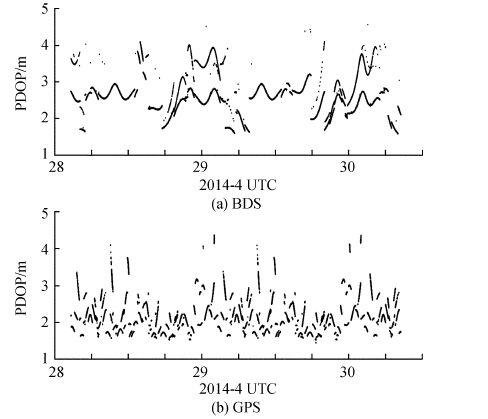
3.2 位置精度因子位置精度因子反映了卫星的几何分布。图 2给出了观测期间北斗与全球定位系统的位置精度因子值。北斗和全球定位系统的位置精度因子值都在1.5~5之间变化,全球定位系统大多数时刻的位置精度因子比较稳定,但是有少数时候较大。北斗的平均值为2.49,全球定位系统为2.12,整体上北斗的更大。这说明,虽然北斗可用卫星数比全球定位系统多,但是卫星几何分布不如全球定位系统[15]。
|
| 图 2 位置精度因子值 Figure 2 Position dilution of precision (PDOP) |
比较图 2与图 1可发现,位置精度因子出现较大值时一般可用卫星数较少。北斗由于某些时刻部分卫星的观测数据缺失,造成了对应的位置精度因子值的跳跃频繁,所以有些时刻看上去对应 “两个” 位置精度因子值。对于北斗,其卫星可用数在每天协调世界时0时左右有一段 “震荡”,其位置精度因子值也在此时有一段 “震荡”。对于全球定位系统,其可用卫星数在每天协调世界时0时左右达到最小,此时位置精度因子值也最不稳定,出现了很多较大值。最终,全球定位系统的位置精度因子出现较大值的频次大于北斗。
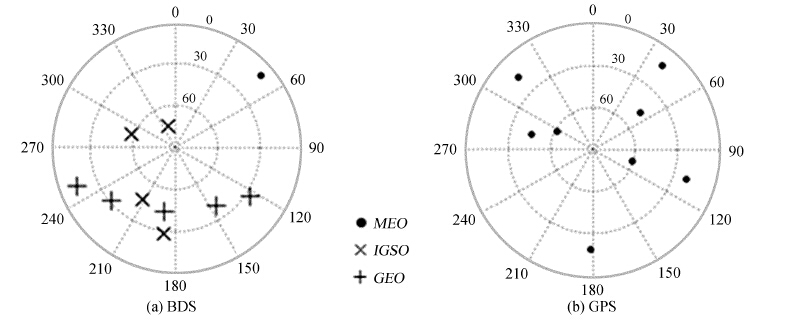
为了进一步说明卫星几何分布对位置精度因子值的影响,图 3给出了协调世界时4月28日4时36分12秒的卫星分布图。该时刻北斗的可用卫星数为10,位置精度因子为1.69;全球定位系统的可用卫星数为8,位置精度因子为1.65。北斗的可用卫星数多于全球定位系统,但位置精度因子却与全球定位系统相当。从卫星几何分布图中可以找出原因:北斗的卫星大多分布在西南方向,而全球定位系统在各个方向都有卫星分布且高度角有大有小。综合来看,全球定位系统的卫星分布优于北斗。
|
| 图 3 4月28日4时36分12秒的卫星分布 Figure 3 Distribution of satellites at 4:36:12,April 28(th) |
由(5)式,单位权中误差由观测方程组的残差矩阵和自由度决定,反映了通过最小二乘法解出的坐标和钟差与各伪距的符合程度。而由导航星历算出的卫星位置和卫星钟差的误差可以等效为伪距误差,故单位权中误差可从整体反映系统各卫星的等效距离误差。
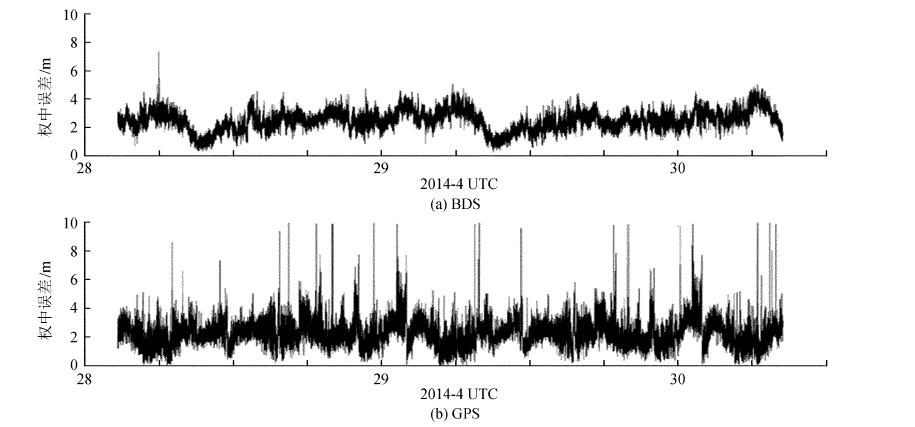
如图 4,北斗的单位权中误差在0~8 m起伏,统计显示有98.61%的时间在4 m以内变化,最大值为7.7 m。全球定位系统的单位权中误差只有97.18%在4 m以内,并且有21个值超过了10 m,最大值达到19.27 m,限于篇幅在此没有显示。这反映了北斗在伪距观测质量方面优于全球定位系统。
|
| 图 4 权中误差 Figure 4 Standard error of unit weight |
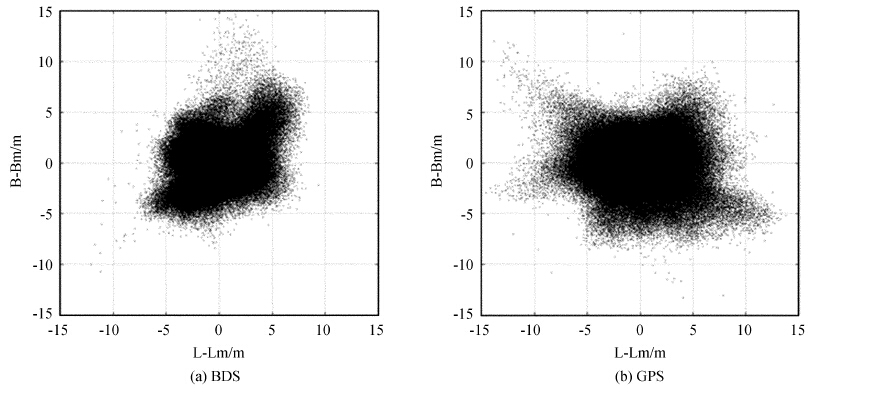
图 5是北斗和全球定位系统在水平方面的点位分布,原点为各自的平均值点。
|
| 图 5 水平定位结果 Figure 5 Horizontal positioning results |
在北方向上北斗和全球定位系统定位结果的质量相当,99%以上的内偏差在8 m以内,不过也有几十个值超过了10 m。在东方向上北斗的内偏差有99.81%在7 m内,而全球定位系统只有99.57%在10 m内。北斗点分布范围比全球定位系统要小,东方向上的粗差远比全球定位系统小。北斗的平均水平内符合精度为3.35 m,全球定位系统为4.22 m。这说明北斗系统中的地球静止轨道卫星保证了北斗在亚洲地区的定位稳定性在东方向上优于全球定位系统。
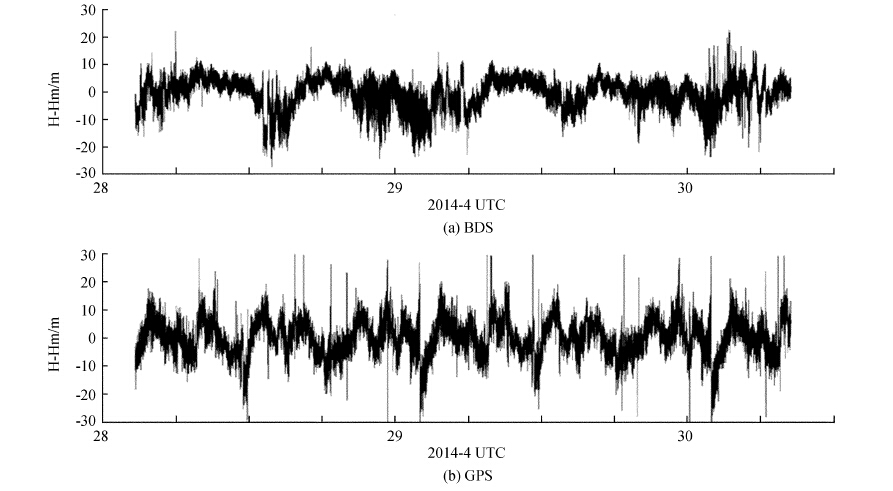
3.5 高程内符合精度图 6分别是北斗和全球定位系统每一历元定位结果的高程与其高程平均值的差值。
|
| 图 6 高程定位结果 Figure 6 Elevational positioning results |
北斗的高程内偏差有97.84%在-12至12 m变化,全球定位系统的高程内偏差有97.83%在-15至15 m变化。北斗高程的内符合精度为4.80 m,而全球定位系统为6.29 m。在稳定性方面北斗比全球定位系统好。高程结果的稳定性与卫星数据的连续性相对应,北斗除在0时附近稳定性较差,其它时刻较好(28日14时例外,下文给出解释);而全球定位系统全天稳定性一般。
北斗的5号卫星在28日14时和15时的导航电文都不可用,可能处于调整中,因此相应的高程结果远差于29日15时。另外5号卫星在29日0时和30日0时的数据频繁缺失,相应的高程结果也较差。可以看出5号卫星作为地球静止轨道卫星在高程测量中发挥着较大的作用。 对于全球定位系统,其粗差出现得较多,而且呈现规律性,高程的粗差与可用卫星数的最小时刻、位置精度因子值和权中误差的较大时刻相对应。
3.6 讨 论对观测期间的定位结果进行统计,得到北斗的伪距单点定位坐标均值:40°0′10.72″ N,116°22′43.11″ E,58.64 m,全球定位系统的坐标均值为:40°0′10.59″ N,116°22′43.04″ E,59.99 m。表 2给出了观测期间北斗和全球定位系统的各项性能参数。这里,三维坐标中只要有一项超过3倍中误差,可认为该定位结果为粗差。
| 可见星数均值 | 权中误差均值/m | 粗差数 | DOP值均值/m | 内符合精度/m | 外符合精度/m | 与标准值差值/m | |||
| BDS | 9 | 2.28 | 111 | HDOP | 1.27 | B | 2.3 | 6.89 | 8.5 |
| VDOP | 1.22 | L | 2.44 | 5.90 | 3.73 | ||||
| PDOP | 2.49 | H | 4.8 | 4.87 | -0.8 | ||||
| TDOP | 0.5 | P | 5.86 | 10.29 | 9.32 | ||||
| GPS | 8 | 2.50 | 199 | HDOP | 1.08 | B | 2.53 | 4.35 | 4.5 |
| VDOP | 1.04 | L | 3.38 | 4.69 | 2.25 | ||||
| PDOP | 2.12 | H | 6.28 | 6.31 | 0.56 | ||||
| TDOP | 0.33 | P | 7.57 | 8.99 | 5.07 |
在卫星定位中,定位精度一般由两个因素决定:其一,位置精度因子,会对测距误差几何放大;其二,测距误差特性。由表 2可知,与全球定位系统相比,尽管北斗的位置精度因子均值稍大,但北斗的内符合精度优于全球定位系统,说明北斗的测距误差小于全球定位系统的测距误差,这一点从权中误差的结果也可以得到佐证。权中误差反映了伪距的噪声水平,观测期间,北斗的权中误差均值为2.28 m,全球定位系统为2.50 m。北斗的测距精度优于全球定位系统,这与文[2]的结论是一致的。
全球定位系统的粗差出现次数为199,频次为1.02%;北斗为111,频次为0.57%,北斗的可用性优于全球定位系统。在包含粗差的统计条件下,北斗的内符合精度(2.30 m,2.44 m,4.80 m)优于全球定位系统(2.53 m,3.38 m,6.28 m)。如果剔除粗差值,两个系统的结果都有所改善,北斗的内符合精度(2.17 m,2.41 m,4.40 m,水平值3.24 m)仍优于全球定位系统(2.40 m,3.08 m,5.57 m,水平值3.90 m)。
由于全球定位系统的高程抖动过大,导致竖直方向外符合精度不如北斗;但北方向和东方向的外符合精度都优于北斗。而从定位坐标均值与标准坐标的差值可以看出,全球定位系统在各方向都优于北斗。均值与标准值的差值主要由轨道误差和钟差残差所致。由北斗的钟差精度因子值(0.50)大于全球定位系统(0.33),可知北斗的钟性能不如全球定位系统。硬件延迟所引起的系统误差可达几米,按导航电文中群时延(Time Group Delay,TGD)参数的定义,全球定位系统使用无电离层组合时无需进行硬件延迟改正,而北斗有两个群时延参数,但目前大多数接收机生成的导航电文只包含一个群时延参数,故无法进行硬件延迟改正[16]。综合来看,北斗的可用性与稳定性优于全球定位系统,但准确性不如全球定位系统。
4 结 语观测时段北斗可用卫星数均值为9,全球定位系统为8。但是由于北斗布网还未完善,在北京可见卫星大都是地球静止轨道卫星,北斗的位置精度因子平均值为2.49,全球定位系统为2.12。北斗的权中误差均值为2.28 m,全球定位系统为2.50 m,说明北斗信号的测距性能优于全球定位系统。由于可见卫星数的变化,北斗和全球定位系统都有粗差出现,北斗出现的频次为0.57%,全球定位系统为1.02%。
北斗和全球定位系统的伪距单点定位结果在北方向上相当,绝大部分在8 m内。东方向上北斗的内偏差在7 m内,优于全球定位系统的10 m。高程上绝大部分在15 m以内,但全球定位系统的高程粗差较多且震动幅度相对较大。北斗的内符合精度优于全球定位系统,但外符合精度不如全球定位系统。
随着北斗系统星座的完善,导航星历产品精度的提高以及接收机的改进,其精度和可用性一定会进一步提高。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报 , 2010 , 39 (1) : 1 –6 Yang Yuanxi. Progress, contribution and challenges of COMPASS/Beidou satellite navigation system[J]. Acta Geodaetica et Cartographica Sinica , 2010 , 39 (1) : 1 –6. |
| [2] | 严丽, 黄丁发, 冯威, 等. COMPASS与GPS伪距单点定位性能比较研究[C]//第三届中国卫星导航学术年会电子文集,S06北斗/GNSS测试评估技术. 2012. |
| [3] | 范磊, 钟世明, 欧吉坤, 等. COMPASS与GPS伪距单点定位精度分析[C]//第四届中国卫星导航学术年会论文集,S8卫星导航模型与方法. 2013. http://cpfd.cnki.com.cn/article/cpfdtotal-wxdh201305003032.htm |
| [4] | 安家春, 王泽民, 胡志刚, 等. 北斗二代在中国及周边海域的定位分析[J]. 大地测量与地球动力学 , 2013 , 33 (3) : 83 –86 An Jiachun, Wang Zemin, Hu Zhigang, et al. Positioning analysis of Beidou-2/COMPASS in China and surrounding seas[J]. Journal of Geodesy and Geodynamics , 2013 , 33 (3) : 83 –86. |
| [5] | Ji Shengyue, Xu Ying, Chen Wu, et al. Comparison of standalone performance between COMPASS and GPS[J]. The Journal of Navigation , 2014 , 67 : 37 –48. DOI: 10.1017/S0373463313000477 |
| [6] | 康四林, 李语强. GPS定位中的误差分析[J]. 天文研究与技术,国家天文台台刊 , 2010 , 7 (3) : 222 –230 Kang Silin, Li Yuqiang. Error analysis of GPS Positioning[J]. Astronomical Research&Technology,Publications of National Astronomical Observatories of China , 2010 , 7 (3) : 222 –230. |
| [7] | Fan Jiangtao, Ma Guanyi. Characteristics of GPS positioning error with non-uniform pseudorange error[J]. GPS Solutions , 2014 , 18 (4) : 615 –623. DOI: 10.1007/s10291-013-0359-z |
| [8] | 何瑞珠, 刘成, 黄康. 卫星定位中的一种分步加权解算方法[J]. 天文研究与技术 , 2015 , 12 (1) : 36 –43 He Ruizhu, Liu Cheng, Huang Kang. A method of multiple-step weighted least-square estimate for satellite positioning[J]. Astronomical Research&Technology , 2015 , 12 (1) : 36 –43. |
| [9] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社. 2003. |
| [10] | Kaplan E D, Hegarty C J. Understanding GPS:principles and applications[M]. Norwood: Artech House. 2006. |
| [11] | Li Xiaojie, Zhou Jianhua, Liu Li, et al. Research on technique of single-satellite orbit determination for GEO satellite of partial subsatellite point[C]//China Satellite Navigation Conference (CSNC) 2013 proceedings. 2013:163-172. |
| [12] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社. 2005, 43-44. |
| [13] | 魏子卿. 2000中国大地坐标系及其与WGS84的比较[J]. 大地测量与地球动力学 , 2008 , 28 (5) : 1 –5 Wei Ziqing. China geodetic coordinate system 2000 and its comparison with WGS84[J]. Journal of Geodesy and Geodynamics , 2008 , 28 (5) : 1 –5. |
| [14] | Li Xingxing, Ge Maorong, Dai Xiaolei, et al. Accuracy and reliability of multi-GNSS real-time precise positioning:GPS, GLONASS, BeiDou, and Galileo[J]. Journal of Geodesy , 2015 , 89 (6) : 607 –635. DOI: 10.1007/s00190-015-0802-8 |
| [15] | Chen Hechin, Huang Yusheng, Chiang Kaiwei, et al. The performance comparison between GPS and BeiDou-2/COMPASS:a perspective from Asia[J]. Journal of the Chinese Institute of Engineers , 2009 , 32 (5) : 679 –689. DOI: 10.1080/02533839.2009.9671550 |
| [16] | 王彬, 刘经南, 隋心. BDS与GPS群延迟的异同分析与应用[J]. 测绘科学 , 2015 , 40 (10) : 142 –145 Wang Bin, Liu Jingnan, Sui Xin. Analysis and research of different between BDS-TGD and GPS-TGD[J]. Science of Surveying and Mapping , 2015 , 40 (10) : 142 –145. |


