2. 中国科学院大学, 北京 100049;
3. 西安卫星测控中心佳木斯深空站, 黑龙江 佳木斯 154002
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Jiamusi Deep Space Station, Xi'an Satellite Control Center, Jiamusi 154002, China
理想情况下,射电望远镜应该能够精确对准要观测的目标射电源。由于射电望远镜的大天线或多或少存在一定的装匹误差,比如:方位轮轨相对于理想的水平面有一点倾斜,方位轴和俯仰轴不垂直,编码器零点有位置偏差,或者因为大天线的重力变形、大气折射等外界因素,使得天线指向总是存在一定误差。射电天文观测通常要求天线的指向误差在十分之一波束宽度以内,这样指向误差引起的信号幅度变化小于3%[1]。原则上,可以通过改进天线机械结构的设计和提高安装精度来提高天线的指向精度,比如采用保型设计等方法。但对几十米口径的大抛物面天线,提高硬件指标不仅会增加建造难度,还使天线造价大幅度升高。具体到工程上,人们不仅仅注意大天线的结构设计,还会对可重复的大天线指向误差采取软件补偿和校准的方式,有效提高天线的指向精度。
国际上大射电望远镜的指向校准大致有两种方式:一种是加装小型光学望远镜进行光学导星,如澳大利亚帕克斯的64 m射电望远镜和意大利萨丁岛的66 m射电望远镜[2];另一种是通过测量射电望远镜在各个方向的指向误差,建立指向误差模型,并在控制天线时利用模型实时修正望远镜的指向。国内的射电望远镜都是这样做的,如上海65 m射电望远镜、密云50 m射电望远镜、昆明40 m射电望远镜和乌鲁木齐25 m射电望远镜。光学导星的方式虽然可以做出好的指向精度,但需要加装硬件设施,且观测时也有一定的局限性,比如:要求观测的射电源邻近有较亮的光学目标用于导星;观测只能在晴朗的夜间使用。相对而言,建立误差模型的方法仅仅是测量和软件层面的改进 ,很容易实现,因此对几乎所有的望远镜,不管是光学的还是射电的,都非常实用。很多望远镜,即使有了光学的指向系统,也配备误差改正的自动修正表。计划建造的塞罗查南托阿塔卡马望远镜(Cerro Chajnantor Atacama Telescope,CCAT)也准备加装光学望远镜来测量天线的指向误差,但最终的指向仍采用误差模型进行内插和校准。当然,在晴夜观测时,塞罗查南托阿塔卡马望远镜可以采用光学导星的方式减小指向误差[3]。
天线的指向误差进行准确和全面的测量。大天线建成一段时间之后,各种环境条件如地面沉降等影响天线指向的因素都相对稳定。这时,对天空中处于各个不同方位、俯仰的很多射电源进行大样本的位置测量,测量出射电源理想位置和实际位置的差以求得大天线的指向误差,构建指向误差模型,还可以分析导致天线指向不准的各种物理因素,用于进一步提高天线的指向精度。其实,如果对天空中几乎所有位置的射电源进行大量的位置测量,得到足够多的天线指向误差数据之后,可以直接使用插值或模型拟合的方式构建指向误差的数值模型或拟合模型。对于插值方法,有拟里兹(Ritz)广义插值法[4]和广义延拓插值法[5]。模型拟合的方法较为普遍使用。主要的数学拟合模型包括:基本参数模型[1, 6-11]、球谐函数模型[7]、半参数回归模型[9]和神经网络模型[12]等。其中,基本参数模型较为广泛使用,因为相比于其他模型,它更易收敛,且拟合结果稳定,物理含义明显,因此具有明显的优势。但常用基本误差模型包含的误差项较少,有时无法精确拟合较为复杂的情况。所以工程实践中已经发展了一些模型改进的形式,以增加模型拟合的精度。
佳木斯66 m射电望远镜是我国目前最大的深空探测天线。观测发现,根据原先的模型校准后指向位置误差仍然相对较大,影响了正常的射电源流量测量。为了解佳木斯66 m射电望远镜的指向误差的具体情况,并提高指向精度,于2015年3月至4月之间,进行了大样本射电源的指向误差测量,并对观测数据进行了分析。本文呈现观测结果后,还针对性地提出了一个误差模型改进的方案。
1 佳木斯66 m射电望远镜的指向误差测量要了解66 m射电望远镜的指向误差,需要对天线各个方位和俯仰上的射电源进行大量的指向误差测量。除了原来望远镜用于天线标校测量的几个常用射电强源外,还从文[13]发布的源表中挑选了几十个强射电点源,选取的基本标准是:
(1) 在观测频段有较大射电流量密度,即射电源非常强;
(2) 对佳木斯66 m射电望远镜而言,因为射电源看起来不可分辨,可被看做点源;
(3) 观测数据在天空分布较为均匀。
另外,为更好地保证观测信噪比,选源的时候还注意避免靠近太阳或非常靠近地面,因为地面或太阳的射电辐射从望远镜的旁瓣进入天线,使得测量信噪比变差;另外所选的射电源也尽量避免靠近银河盘,使得银河系弥漫射电辐射对测量结果贡献不大,有利于指向的测量精度。
选定一批射电源之后,利用66 m射电望远镜进行十字扫描观测,即望远镜对射电源沿两个相互垂直的方向(即方位和俯仰)进行扫描观测,在扫描过程中记录天线的指向及对应时刻天线辐射计测得的功率值。对天线沿方位或俯仰扫描一个射电点源之后,得到功率随方位或俯仰值变化的一条曲线。大天线存在指向误差时,功率曲线最大值对应的坐标与射电源当时的坐标有一定的偏差。通过对射电源沿方位方向扫描,可以得到天线在方位和俯仰二维坐标中的方位指向误差;通过对射电源沿俯仰方向扫描,可以得到天线在方位和俯仰二维坐标中的俯仰指向误差。因此,佳木斯66 m天线对每个射电源的方位和俯仰分别扫描,每次对射电源的扫描观测一般能得到数十个数据点,每个数据点含有4个测量参量,具体见表 1。
| 扫描得到的参数 | 俯仰扫描得到的参数 | ||
| AZr | 扫描曲线的实际峰值方位 | ELr | 扫描曲线的实际峰值俯仰 |
| AZ0 | 射电源的理论方位 | EL0 | 射电源的理论俯值 |
| ΔAZ | 方位实际值与理论值之差 | ΔEL | 俯仰实际值与理论值之差 |
| FAZ | 射电源流量 | FEL | 射电源流量 |
这里, ΔAZ= AZr- AZ0, ΔEL= ELr- EL0。理论上,扫描射电源得到功率变化曲线特别是峰值相关的参数提取之后,通过比较天线实际指向的坐标值与理论值之差( ΔAZ或 ΔEL)得到天线在该方向的指向误差。
由于射电望远镜对射电源的十字扫描数据是离散的,还受到噪声的干扰,所以不能从数据直接得到功率变化曲线峰值的准确位置,进而没法得到天线的指向误差。考虑到天线扫描得到的主波束响应曲线形状类似高斯函数,66 m射电望远镜在S波段的主波束宽度(功率的半高全宽)是6.9″,所以扫描射电源得到的功率变化曲线实际上是射电源的强度分布与望远镜的主波束响应函数做卷积得到的曲线。对于指向测量中的绝大部分射电源与望远镜的6.9″主波束相比角直径很小,因此响应曲线依旧是高斯函数。所以,工作中用高斯函数:
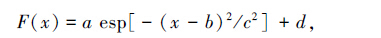
|
(1) |
拟合扫描观测得到的功率变化曲线,找出功率变化曲线的峰值位置。其中, x 为观测采样点序号; a、b、c、d 为待拟合的高斯参数。实际指向测量时最在乎的是高斯函数中心的偏离量 b ,即高斯曲线峰值对应时间序列的 x 值。因为不同俯仰高度时扫描射电源的方位和速度不同,需要将高斯拟合得到的偏离量 b 转换为实际方位差或俯仰差的数值:
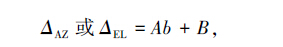
|
(2) |
其中, A、B 为线性拟合的参数。对每个射电源的方位和俯仰分别扫描后,通过上面的拟合得到天线指向该处的误差 ΔAZ和 ΔEL。考虑到扫描射电源时使用的是地平坐标,扫描方向也是方位和俯仰,因此得到的偏差也是方位和俯仰的偏差。在高俯仰扫描射电源时,拟合得到的实际方位误差与俯仰角有关。高俯仰时天线实际指向精度应该是方位误差乘该处俯仰的余弦。因此,指向天空不同方位和俯仰的真正指向误差应该是
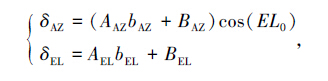
|
(3) |
其中, bAZ、 AAZ、 BAZ为方位扫描数据拟合的 b、A、B 值; EL0为 bAZ采样点对应的射电源理论俯仰值; bEL、 AEL、 BEL为俯仰扫描数据拟合的 b、A、B 值。
射电源强度不同,扫描得到的功率曲线的信噪比不同。由不同信噪比曲线拟合指向误差时,得到不同的拟合精度。当扫描功率曲线信噪比高于20时,拟合误差约为±2″ (95%置信区间);当观测数据信噪比小于5时,拟合误差约为±10″ (95%置信区间)。
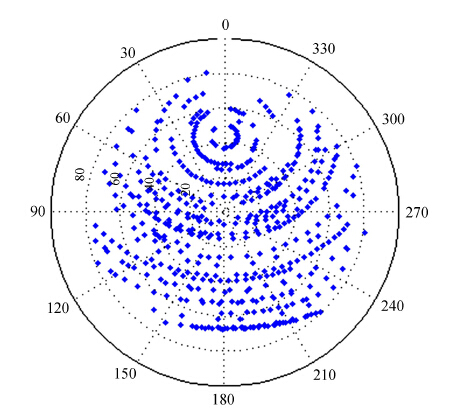
2015年3月17日至4月13日进行了66 m射电望远镜的大量指向误差测量,得到有效测量数据499个,如图 1。
|
| 图 1 指向误差测量点在地平坐标下的数据分布 Figure 1 Data distribution in horizontal coordinate system of pointing measurements |
为了解天线指向误差的具体情况,图 2显示了方位和俯仰误差测量数据 δAZ和 δEL随方位、俯仰的变化。对 n =499个误差测量数据进行均方根计算[11, 14],然后得到总误差的均方根 δ 。它与每个点从方位误差和俯仰误差得到单个测量点的总位置误差再算均方根是一样的:
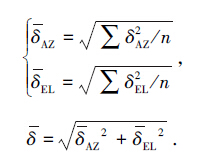
|
(4) |
|
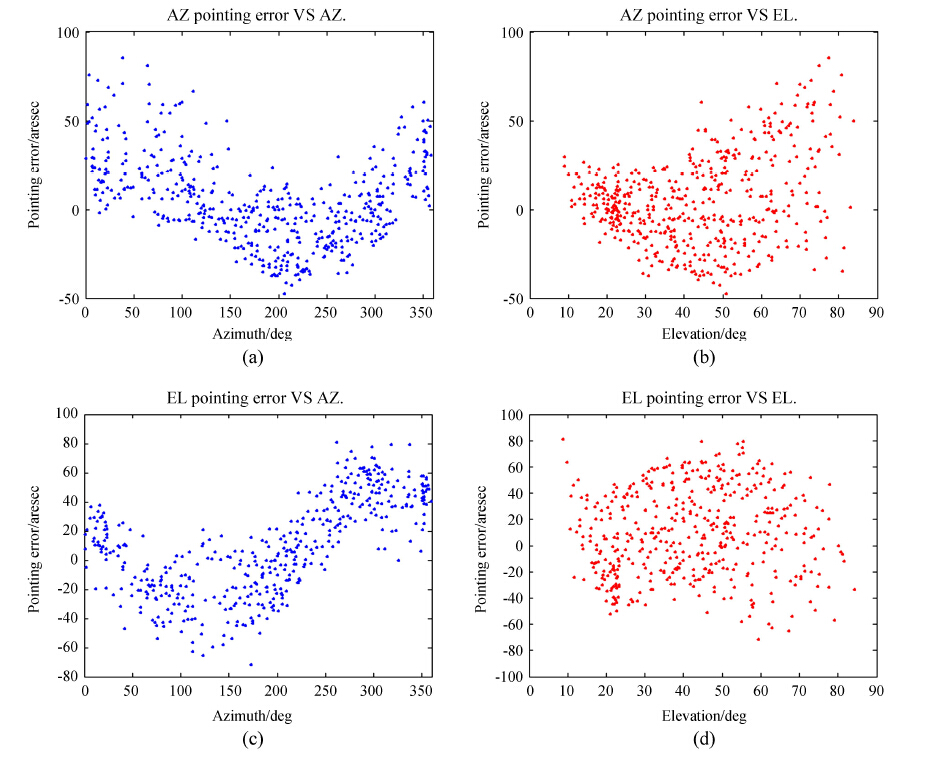
| 图 2 观测得到的天线指向误差中方位误差 δAZ(a,b)和俯仰误差 δEL(c,d)随方位(a,c)和俯仰(b,d)变化 Figure 2 The variation of pointing uncertainties δAZ(a,b) and δEL(c,d) with azimuth (a,c) and elevation (b,d) |
从方位误差得到的天线方位指向误差均方根 δAZ 为24.9″,俯仰指向误差均方根 δEL 为37.6″,总误差均方根 δ 为45.1″。
2 指向误差的模型改正从图 2可以看出,佳木斯66 m射电望远镜的指向误差随方位和俯仰有明显的变化趋势。本节希望改进射电望远镜的指向模型,克服图 2中的系统误差。
2.1 基本参数模型目前测量的望远镜指向误差结果是望远镜的真实指向误差经过基本参数模型改正过的效果。所谓的基本参数模型,就是根据大天线最主要的几个可能的误差源建立的数学模型[11]:
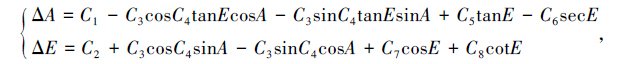
|
(5) |
其中,每个参数都有明确的物理意义: A 为指向测量的方位; E 为指向测量的俯仰;Δ A 为方位指向误差;Δ E 为俯仰指向误差; C1至 C8为8个参数,分别表示了: C1方位编码器零点误差; C2俯仰编码器零点误差; C3方位倾斜误差;(π/2- C4)方位倾斜方向的方位坐标;(π/2- C5)方位轴与俯仰轴夹角; C6电轴指向偏差; C7重力变形; C8大气折射。原则上,可以通过对一批射电源的指向误差测量数据 A、E、 Δ A 和Δ E 值,通过最小二乘法解算得到 C1至 C8 8个参数。
很显然,66 m射电望远镜使用基本参数模型之后得到图 2的结果并不理想。把早期模型扣除的方位和俯仰误差的数值计算出来,加到图 2的数据中,得到初始误差数据。然后对所有方位和俯仰初始误差数据重新使用(5)式给出的基本参数模型进行拟合,得到了一个新的基本参数模型。利用新的基本参数模型,对原先数据中的系统误差进行扣减,得到天线方位指向误差均方根 δAZ 为12.5″,俯仰指向误差均方根 δEL 为17.3″,总误差均方根 δ 为21.4″。利用新基本参数模型修正后的指向误差数据点随方位、俯仰的分布图如图 3。

|
| 图 3 利用新的基本参数模型改正后方位误差δAZ(a,b)和俯仰误差δEL(c,d)随方位(a,c)和俯仰(b,d)变化 Figure 3 The variation of pointing uncertainties δAZ(a,b) and δEL(c,d) with azimuth (a,c) and elevation (b,d) after the correction of a new basic-parameter model |
从图 3的结果可以看出基本参数模型可以明显地改进天线的指向精度。但还是可以看到天线方位误差随方位和俯仰仍然有变化趋势,天线俯仰误差数据点分布也随俯仰有明显的变化趋势。为了消除这种系统误差,进一步提高天线的指向精度,提出一种增强型的基本参数模型。
基本参数模型考虑了几个主要误差项的零阶分量,它们各自贡献明显,影响最大,因此能够修正测量到的主要误差,所以基本参数模型具有通用性。但超大口径天线因为方向束比较小,对观测指向精度的要求非常高,误差项中除了零阶分量之外高阶分量不能忽略。分析认为,经过基本参数模型扣除之后,66 m射电望远镜的指向误差的变化趋势是由两个参数的高阶误差引起的:一是方位轴和俯仰轴夹角;二是天线的重力变形。因此本文尝试对基本误差模型(5)式中 C5(方位轴和俯仰轴夹角)和 C7(重力变形)两个参量进行傅里叶级数展开,使模型包括一阶分量。两个参数加入一阶分量后变成:
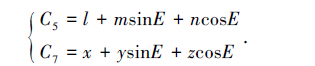
|
(6) |
代入(5)式的基本参数模型后得到:
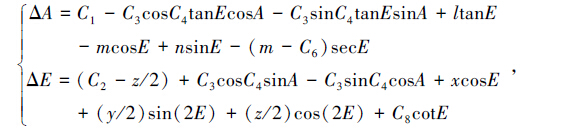
|
(7) |
将12个模型参数统一用 Pi 的形式整理得到新的增强基本参数指向误差模型:
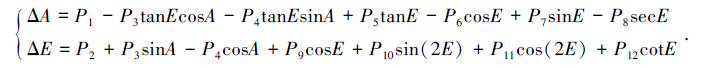
|
(8) |
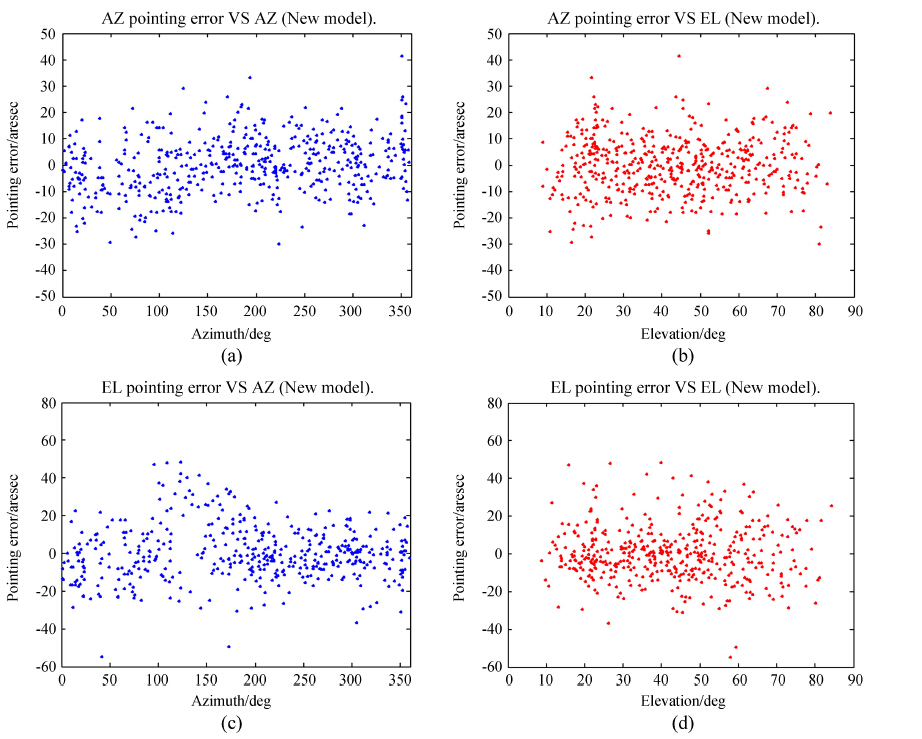
将上面得到的初始误差数据利用 (8)式的增强基本参数模型进行拟合,得到了模型修正后指向误差的残差,如图 4。方位指向误差均方根δAZ 为10.5″,俯仰指向误差均方根 δEL 为14.5″,总误差均方根 δ 为17.9″。增强基本参数模型不仅使指向误差残差变小,更重要的是使图 4中方位和俯仰指向误差没有明显的随方位或俯仰的变化趋势,达到了非常理想的效果。表 2总结了分别使用文中3种不同模型改正后得到的天线指向误差,可以明显看出指向精度的改善情况。
|
| 图 4 利用增强基本参数模型对初始指向数据改正后的方位误差 δAZ(a,b)和俯仰误差 δEL(c,d)随方位(a,c)和俯仰(b,d)变化 Figure 4 The variation of pointing uncertainties δAZ(a,b) and δEL(c,d) with azimuth (a,c) and elevation (b,d) after the correction of the enhanced basic-parameter model |
| 方位误差均方根 δAZ | 俯仰误差均方根 δEL | 总误差均方根 δ | |
| 原基本参数模型修正后观测得到的指向误差 | 24.9 | 37.6 | 45.1 |
| 新基本参数模型补偿 | 12.5 | 17.3 | 21.4 |
| 增强基本参数模型补偿 | 10.5 | 14.5 | 17.9 |
本文选取天空中分布比较均匀的大量射电点源,对66 m射电望远镜的指向误差进行了大样本和大天区覆盖的测量。把测量数据还原成初始误差数据后,对初始误差数据拟合得到了新的基本参数模型。利用新模型对误差改正后,天线的指向误差大幅减小。但指向误差的残差数据仍然呈现随方位和俯仰变化的趋势。分析发现它可能是方位轴与俯仰轴夹角和重力变形两个参量随不同位置的高阶项引起的。通过引入模型中两个参数的一阶项,构建了增强基本参数模型,拟合结果显示它能够有效移除指向误差的系统性变化,进一步提升佳木斯66 m射电望远镜的指向精度。
致谢:
感谢佳木斯深空站全体工作人员的大力支持,特别感谢佳木斯深空站侯俊楠、梁琪、岳世磊、孟宪波等人为观测提供的帮助。
| [1] | 赵彦, 张新锋, 施浒立. 基于四元数的射电望远镜指向误差分析方法[J]. 机械科学与技术 , 2009 , 28 (10) : 1359 –1363 Zhao Yan, Zhang Xinfeng, Shi Huli. Pointing error analysis of a radio telescope using quaternion[J]. Mechanical Science and Technology for Aerospace Engineering , 2009 , 28 (10) : 1359 –1363. |
| [2] | Poppi S, Pernechele C, Pisanu T, et al. High-precision pointing with the Sardinia Radio Telescope[C]//Proceedings of SPIE. 2010. http://cn.bing.com/academic/profile?id=2121662878&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | Assawaworrarit S, Padin S. An optical pointing telescope for radio astronomy[J]. Publications of the Astronomical Society of the Pacific , 2012 , 124 (913) : 242 –246. DOI: 10.1086/664969 |
| [4] | 施浒立, 古天龙. 雷达天线和天文望远镜指向误差修正的数学模型,拟里兹广义插值[J]. 电子机械工程 , 1987 (5) : 1 –7 |
| [5] | 孔德庆, 施浒立, 张喜镇, 等. 射电望远镜指向误差的广义延拓插值修正方法[J]. 西安电子科技大学学报:自然科学版 , 2008 , 35 (1) : 157 –161 Kong Deqing, Shi Huli, Zhang Xizhen, et al. Radio telescope pointing model based on the generalized extended interpolation correction method[J]. Journal of Xidian University:Natural Sciences , 2008 , 35 (1) : 157 –161. |
| [6] | 袁惠仁, 彭云楼, 薛吟章. 天线参数的射电天文测量[M]. 北京: 电子工业出版社. 1986, 147-172. |
| [7] | 张晓祥, 吴连大. 望远镜静态指向模型的基本参数[J]. 天文学报 , 2001 , 42 (2) : 198 –205 Zhang Xiaoxiang, Wu Lianda. The basic parameters of telescope static point model[J]. Acta Astronomica Sinica , 2001 , 42 (2) : 198 –205. |
| [8] | 何秋会, 刘利利, 汪翊鹏, 等. 南京大学65 cm天文望远镜指向精度的修正研究[J]. 南京大学学报:自然科学版 , 2005 , 41 (4) : 356 –363 He Qiuhui, Liu Lili, Wang Yipeng, et al. Correction of pointing accuracy of NJU-65cm telescope[J]. Journal of Nanjing University:Natural Sciences , 2005 , 41 (4) : 356 –363. |
| [9] | 赵彦. 大射电望远镜指向误差建模分析与设计研究[D]. 西安:西安电子科技大学, 2008. |
| [10] | Kong Deqing, Wang Songgen, Wang Jinqing, et al. A new calibration model for pointing a radio telescope that considers nonlinear errors in the azimuth axis[J]. Research in Astronomy&Astrophysics , 2014 , 14 (6) : 733 –740. |
| [11] | 虞林峰, 王锦清, 赵融冰, 等. TM65 m射电望远镜指向模型的建立[J]. 天文学报 , 2015 , 56 (2) : 165 –177 Yu Linfeng, Wang Jinqing, Zhao Rongbing, et al. Pointing model establishment of TM65 m radio telescope[J]. Acta Astronomica Sinica , 2015 , 56 (2) : 165 –177. |
| [12] | 朱程广, 郭唐永, 邹彤, 等. BP神经网络在卫星激光测距望远镜指向误差建模中的应用[J]. 大地测量与地球动力学 , 2013 , 33 (5) : 150 –153 Zhu Chengguang, Guo Tangyong, Zou Tong, et al. Application of BP neural network in pointing error model of satellite laser ranging telescope[J]. Journal of Geodesy and Geodynamics , 2013 , 33 (5) : 150 –153. |
| [13] | Condon J J, Yin Q F. Offset pointing calibrators for large radio telescopes[J]. Publications of the Astronomical Society of the Pacific , 2001 , 113 (781) : 362 –365. DOI: 10.1086/pasp.2001.113.issue-781 |
| [14] | 高冠男, 汪敏, 施硕彪, 等. 云台40 m射电望远镜的指向误差校正[J]. 天文研究与技术,国家天文台台刊 , 2007 , 4 (2) : 188 –194 Gao Guannan, Wang Min, Shi Shuobiao, et al. Pointing calibration for the 40m radio telescope in Yunnan Observatory[J]. Astronomical Research&Technology,Publications of National Astronomical Observatories of China , 2007 , 4 (2) : 188 –194. |


