2. 中国科学院空间天文与技术重点实验室, 北京 100012;
3. 中国科学院大学, 北京 100049
2. Key Laboratory of Space Astronomy and Technology, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
由于孔径的衍射效应,传统望远镜的成像分辨率受限于入瞳口径。受加工工艺和成本等因素的制约,光学系统的口径不可能无限增大[1]。为了解决这个问题,研究人员提出了光干涉的方法。随着技术的发展,Fizeau型光干涉技术因具有一定的成像视场和对面源短时成像的特点,受到越来越多的重视,成为当前的研究热点之一。早在1996年,美国空军武器实验室就启动了用于建立对地观测的可展开式望远镜阵列UltraLITE[2]项目。
结合近年来蓬勃发展的小卫星星座技术,人们提出了基于小卫星的Fizeau型光干涉成像系统。基本方法是:在每个小卫星上各自携带一台小口径望远镜,在中心的主卫星上携带合光成像望远镜,子卫星和主卫星在空间上按一定的位置排布,来自各子望远镜的光束在合光成像望远镜的焦面上相干叠加,干涉成像。这种形式的光干涉成像系统,受小卫星避撞设计的需要,以及小卫星有效载荷质量和体积的限制,子望远镜的口径和要实现的衍射极限分辨率所对应的口径相比,必然差别很大,属于稀疏度很大的光学综合孔径系统。此时,由于UV覆盖不全,系统不可避免地对相应的空间频率在采样时出现缺失。为了克服UV覆盖不全的影响,对面源目标的空间频率信息进行更好的采样,可以通过改变子卫星和主卫星的相对位置来改变系统采样频率的覆盖范围,获得之前缺失的空间频率采样信息,即获得不同基线布局下的干涉图。再经过图像合成和逆滤波处理,最终得到包含目标较完整信息的图像。通过这样的方法,使合成的图像分辨率等效为一个更大口径光学系统的分辨率,达到高分辨率成像的目的。
通常的合成方法是将这些在不同基线下得到的图像在对齐的基础上[3]进行叠加再解卷积,但是由于采集的图像受子望远镜口径较小、积分时间受限等各种因素的影响,信噪比通常都不高。仿真实验发现,当得到的干涉图在信噪比较低的情况下,采用直接叠加再解卷积的处理方法效果不理想。为了提高图像质量,本文提出将不同基线下获得的图像通过相应的频域滤波器,将高信噪比的频域信息提取出来再合成,以减少合成图像中包含的噪声,从而获得更好的合成图像。
1 原理概述成像过程可以看作是目标物体频率函数F(fx,fy )与光学传递函数OTF(fx,fy)乘积后输出像频谱函数G(fx,fy)。在非相干光照射下,衍射受限系统可认为是只改变了输入的各频率光强分量而不改变它们的位相,光学传递函数在数值上等于调制传递函数MTF:
| $\begin{gathered} MTF\left( {{f_x},{f_y}} \right) = \left| {OTF\left( {{f_x},{f_y}} \right)} \right| = \hfill \\ \frac{{P\left( {\lambda f{f_x},\lambda f{f_y}} \right) \otimes P\left( {\lambda f{f_x},\lambda f{f_y}} \right)}}{{\int {\int_{ - \infty }^{ + \infty } {P\left( {x,y} \right){\text{dxdy}}} } }} \hfill \\ \end{gathered} $ | (1) |
其中,$ \otimes $表示自相关符号;P(λf fx,λf fy)是孔径函数。
稀疏孔径成像系统在理想情况下可以看作是由N个直径为d的圆形孔径构成,在数学上可以表示为一个子孔径光瞳函数与δ函数阵列的卷积,即
| $P\left( {x,y} \right) = circ\left( {\frac{{\sqrt {{x^2} + {y^2}} }}{{d/2}}} \right) * \sum\limits_{n = 1}^N {\delta \left( {x - {x_n},y - {y_n}} \right)} $ | (2) |
其中,P(x,y)是光瞳函数;N是子孔径个数;circ()是圆域孔径函数;(xn,yn)是第n个子孔径光瞳的中心坐标。
Golay3是结构最简单的二维阵列结构,由3个圆形子孔径组成,而且这3个圆心依次位于一个等边三角形的3个顶点上[4]。
从(2)式可以推导出Golay3型稀疏孔径的归一化调制传递函数为
| $MTF = MT{F_d} + \frac{1}{3}MT{F_d} * {\Sigma _i}{\Sigma _j}\delta \left( {\xi - \frac{{{x_i} - {x_j}}}{{\lambda f}},\eta - \frac{{{y_i} - {y_j}}}{{\lambda f}}} \right)$ | (3) |
其中,(xi-xj,yi-yj)表示子孔径的相对位置。
根据(3)式,可以将稀疏孔径系统的调制传递函数看作是由分布在不同位置上,强度为1/3倍(零频除外)的单个子孔径的调制传递函数组合而成。除零频外,其它调制传递函数分布的位置都与子孔径排布有关,也就是说如果已知调制传递函数的位置分布就可以推算出子孔径的位置排布。当系统调制传递函数对空间采样频率覆盖的一些区域出现零值或严重衰减时,就可以找到相应的空间位置增加孔径排布进行优化,最后将这些在不同排布(即不同基线)下得到的退化图进行合成处理。
稀疏孔径系统主要的噪声有光子噪声及CCD噪声等,总噪声分布近似为高斯分布,一般认为是零均值的高斯白噪声[5],即功率谱密度在整个频域内均匀分布的噪声。已知单幅退化图的噪声功率为ni,如果将退化图直接叠加就相当于直接叠加了∑ini倍的噪声。
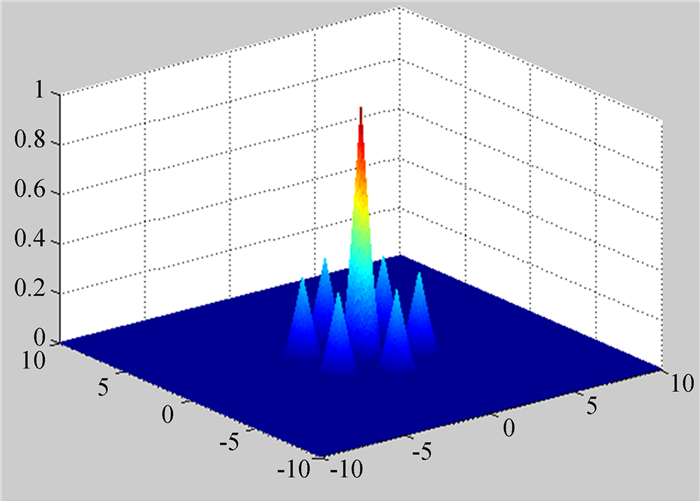
通过子孔径的排布和系统调制传递函数之间的计算关系,可以很容易了解到退化图在不同频域范围内的信噪比情况。以某一种子孔径排布得到的调制传递函数为例,如图 1。图中,中间主峰的峰值表示能通过系统的信号强度最大为1倍,周围次峰则表示能通过的信号强度最大只有原来的1/3,其余值为0的部分,表示相应频域范围内无有效信号通过。对应得到的干涉图信噪比强度的最大值分布分别为$101g\left( {\frac{{{P_s}}}{{{P_n}}}} \right)$、$101g\left( {\frac{{{P_s}}}{{{P_n}}} \cdot \frac{1}{3}} \right)$、0,其中,Ps和Pn分别代表信号和噪声的有效功率。
|
| 图 1 某子孔径排布的调制传递函数示意图 Fig. 1 The MTF of a sub-aperture configuration |
因此,本文针对各种基线排布定义了相应的频域滤波器Hi,将每幅图中频域信噪比较高部分的信号提取出来再合成。由于每幅干涉图的滤波器Hi加权为1,而且范围不完全重复,这样得到的最终合成图的噪声量∑iHi·ni明显小于通过直接叠加得到的,信噪比有了显著的提升。
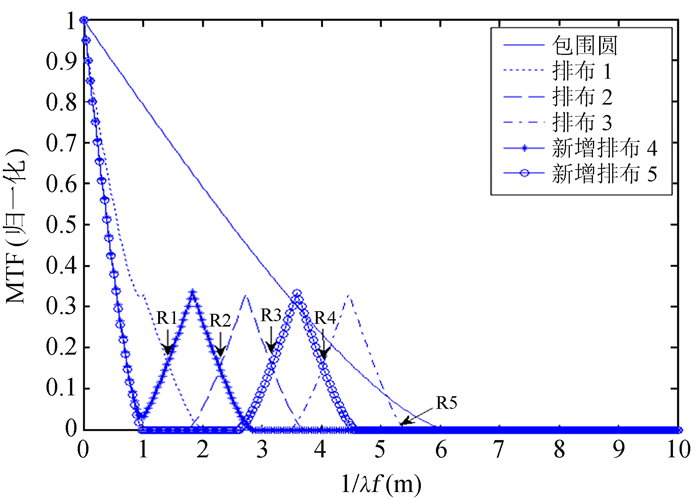
2 图像频率提取及合成方法设单个子孔径直径为1 m。从系统子孔径相切开始,以子孔径直径为间距向外挪动子孔径两次共得到3种不同的排布。此时外接最大包围圆直径为6.15 m。根据这3种排布得到了3种不同分布的调制传递函数。由于发现空间频率信息分别在排布1与排布2、排布2与排布3截止频率交接处附近明显衰减,所以增加新的子孔径排布4和5,对这两交界附近的调制传递函数进行补偿和增强。优化后,这5种排布的调制传递函数在最大截止频率方向的部分截面示意图(在同一坐标系) 如图 2。
|
| 图 2 优化后各排布的调制传递函数部分截面图 Fig. 2 The optimized sectional view of partial MTF for every sub-aperture configuration |
与稀疏孔径系统成像质量相当的单孔径直径称作等效口径。由于稀疏孔径系统的调制传递函数与单孔径系统相比,分布复杂,形状不规则,目前尚没有计算等效口径的统一方法[6]。从图 2可以看出,当前系统最大截止频率5.4/λf(m)明显小于系统包围圆所对应的6.15/λf(m)。所以选最大截止频率对应的口径作为系统等效口径,此处为5.4 m。
在这5种不同的子孔径排布下,获取5幅不同的图像(记作g1、g2、g3、g4和g5)。将这5幅图像通过傅里叶变换到频域(记作G1、G2、G3、G4和G5)。根据各自调制传递函数的分布,分别定义各自的频域滤波器,如(4)~(8)式。其中,H1为低通滤波器;H2、H3、H4和H5分别是不同通带范围的带通滤波器。
| ${H_1}\left( {u,v} \right) = \left\{ \begin{gathered} 1,r \leqslant {R_1} \hfill \\ 0,r{\text{ > }}{R_1} \hfill \\ \end{gathered} \right.$ | (4) |
| ${H_2}\left( {u,v} \right) = \left\{ \begin{gathered} 1,{R_1} \leqslant r \leqslant {R_2} \hfill \\ 0,r{\text{ > }}{R_2} \hfill \\ 0,r{\text{ < }}{R_1} \hfill \\ \end{gathered} \right.$ | (5) |
| ${H_3}\left( {u,v} \right) = \left\{ \begin{gathered} 1,{R_2} \leqslant r \leqslant {R_3} \hfill \\ 0,r{\text{ > }}{R_3} \hfill \\ 0,r{\text{ < }}{R_2} \hfill \\ \end{gathered} \right.$ | (6) |
| ${H_4}\left( {u,v} \right) = \left\{ \begin{gathered} 1,{R_3} \leqslant r \leqslant {R_4} \hfill \\ 0,r{\text{ > }}{R_4} \hfill \\ 0,r{\text{ < }}{R_3} \hfill \\ \end{gathered} \right.$ | (7) |
| ${H_5}\left( {u,v} \right) = \left\{ \begin{gathered} 1,{R_4} \leqslant r \leqslant {R_5} \hfill \\ 0,r{\text{ > }}{R_5} \hfill \\ 0,r{\text{ < }}{R_4} \hfill \\ \end{gathered} \right.$ | (8) |
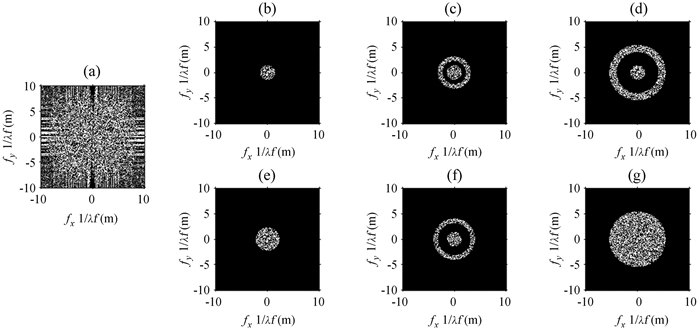
利用这些频域滤波器可以将5幅图中信噪比较好的频率信息提出来。提取及合成方法如图 3。图像频谱合成方法如(9)式:
| ${G_{合成}} = {G_1}{H_1} + {G_2}{H_2} + {G_3}{H_3} + {G_4}{H_4} + {G_5}{H_5}$ | (9) |
|
| 图 3 空间频率信息提取及合成. (a)原始图像频率信息;(b)从孔径排布1提取的频率信息;(c)、(d)、(e)和(f)分别对应从孔径排布2、3、4和5提取的频率信息;(g)合成图像频率信息 Fig. 3 Frequency extraction and synthesis. (a) The frequency of the original objective image; (b) The partial frequency extracted from the degraded image of configuration 1; (c) (d) (e) and (f) The corresponding partial frequency extracted from the degraded image of new configuration 2, 3, 4 and 5; (g) The final synthesized degraded image |
频谱直接叠加如(10)式:
| ${G_{直接叠加}} = {G_1} + {G_2} + {G_3} + {G_4} + {G_5}$ | (10) |
在仿真实验中引入加性高斯白噪声,当信噪比为35 dB和25 dB时分别得到退化图如图 4。

|
| 图 4 不同方法得到的仿真图像. (a)等效口径图像;(b)直接叠加得到的合成图像;(c)频域提取方法得到的合成图像 Fig. 4 Degraded images obtained by different methods. (a) The degraded image obtained by effective Diameter method; (b) The synthesized degraded image obtained by overlapping frequency directly; (c) The synthesized degraded image obtained by frequency filtrations |
从图 4可以看出,当图像信噪比下降后,直接叠加的合成图像像质逐渐变差,此时采用频域提取的合成图像像质占优。
3 图像复原(解卷积)及评价由不同基线图像合成的图像需经过解卷积才能更好地恢复图像。逆滤波是解卷积最直接的方法,设G(u,v)为退化图像的傅里叶谱,H(u,v)为点扩散函数的傅里叶谱,则估计的原始图像的傅里叶谱$\hat F$(u,v)为
| $\hat F\left( {u,v} \right) = \frac{{G\left( {u,v} \right)}}{{H\left( {u,v} \right)}}$ | (11) |
维纳滤波(最小均方误差滤波)是对逆滤波方法的改进。维纳滤波方法综合考虑了退化函数和噪声的统计特性,以减少噪声的影响,如(12)式:
| $W\left( {u,v} \right) = \frac{{{H^ * }\left( {u,v} \right)}}{{\left| {H{{\left( {u,v} \right)}^2}} \right| + \gamma \left[{{S_n}\left( {\left( {u,v} \right)} \right)/{S_f}\left( {u,v} \right)} \right]}}$ | (12) |
其中,*表示共轭;Sn(u,v)/Sf(u,v)是噪声功率谱和原始信号功率谱的比值。当噪声的统计特性未知时,常用一个常数K近似。若γ=1,W(u,v)是维纳滤波器;若γ=0,则系统变成了单纯的去卷积滤波器。
由于图像经过频率提取和合成后,合成图的噪信比有较明显的起伏规律。因此,在去解卷积滤波时,对维纳滤波器也进行了相应的改进:在对应不同的区域,根据合成图噪信比的不同采用了不同的K值。去卷积后的复原图如图 5。

|
| 图 5 不同方法得到的复原效果. (a)等效满口径复原图;(b)直接叠加得到的复原图;(c)频域提取方法得到的合成复原图 Fig. 5 Reconstructional images obtained by different methods. (a) The reconstructional image obtained by effective Diameter method; (b) The reconstructional synthetic image obtained by overlapping frequency directly; (c) The reconstructional synthetic image obtained by frequency filtrations |
对于图像的复原效果,除了主观判断外,采用传统的均方误差(Mean Squared Error,MSE)法和当前国际上比较流行的SSIM(Structural Similarity)法。均方差法基于误差理论,将图像看作是一个个孤立的点,通过计算每个点的灰度值差异而对图像进行评测,见(13)式。SSIM法是对图像在亮度、对比度、结构3个层面上分别进行量化,通过加权相乘获得结构相似值,综合考虑了人类视觉对图像结构性信息的提取功能,比均方差法更符合人类的视觉特性[7],见(14)式:
| $MSE = {e^2} = \mathop {\mathop {\lim }\limits_{X \to \infty } }\limits_{Y \to \infty } \frac{1}{{XY}}\int\limits_{ - X}^{ + X} {\int\limits_{ - Y}^{ + Y} {\left[{\hat f\left( {x,y} \right) - f{{\left( {x,y} \right)}^2}} \right]{\text{dxdy}}} } $ | (13) |
| $MSSIM\left( {f,\hat f} \right) = \overline {SSIM} = \frac{1}{M}\sum\limits_{i = 1}^M {l{{\left( {f,\hat f} \right)}^\alpha }c{{\left( {f,\hat f} \right)}^\beta }s{{\left( {f,\hat f} \right)}^\gamma }} $ | (14) |
其中,f(x,y)表示参考图像;$\hat f$(x,y)表示待评价图像;α 、β、γ为加权系数;l(f,$\hat f$)、c(f,$\hat f$)、s(f,$\hat f$^)为相应的亮度、对比度、结构比较函数。
均方根值越小,表示待评价图像和参考图像越相似;结构相似度均值越大,则表示结构相似值越高,说明待评价图像和参考图像的相似度越高。
在不同信噪比下得到的退化图经过解卷积复原后,分别计算均方根和结构相似度均值,见表 1。
| 信噪比35 | 图(a) | 图(b) | 图(c) |
| MSSIM | 0.976 8 | 0.791 9 | 0.800 3 |
| MSE | 0.000 6 | 0.003 3 | 0.003 1 |
| 信噪比25 | 图(a) | 图(b) | 图(c) |
| MSSIM | 0.916 6 | 0.663 0 | 0.744 1 |
| MSE | 0.001 9 | 0.003 5 | 0.003 0 |
| 图(a)是以原图为评价参考, 图(b)和图(c)都是以图(a)为评价参考 Fig (a) is with reference to the original image; (b) and (c) are with reference to Fig (a) |
|||
结合图 5和表 1可以看出,当信噪比为35 dB时,对合成图(c)的客观评价指标比对直接叠加图像(b)的客观评价指标只是稍微好一点,从主观上观察,人的眼睛基本分不出哪幅图更好。
然而当信噪比下降到25 dB时,对合成图(c)客观评价指标就明显比对直接叠加图像(b)的客观评价值要好一些。在用人眼进行主观评价时,能明显看出合成图(c)中的图像细节更清晰。
4 结论当原始图像的信噪比受限时,利用频域抽取算法将在不同子孔径排布下得到的干涉图合成为一幅包含较完整目标信息的退化图像,再经过改进的维纳滤波算法得到了最终较清晰的复原图像。由于保留了各幅干涉图频域中信噪比较高的部分,在解卷积复原后,其图像质量比直接叠加得到的有明显提升,采用人眼判读和客观评价的方法都显示,该方法能更好地恢复原图像的结构信息。
致谢:本文得到王景宇研究员、薛建伟博士、宋卫强工程师的帮助,在此一并致谢。
| [1] | van Belle G T, Meinel A B, Meinel M P. The scaling relationship between telescope cost and aperture size for very large telescopes[C]// Proceedings of SPIE. 2004: 563-570. |
| [2] | Powers M, Leitner J, Hackney E, et al. Assessment of a large aperture telescope trade space and active opto-mechanical control architecture[C]// Proceedings of IEEE Aerospace Conference.1997: 197-229. |
| [3] | 高莉莉, 刘忠, 金振宇. 综合孔径干涉望远镜的高分辨率图像重建[J]. 天文研究与技术——国家天文台台刊, 2009, 6(4): 327-333. Gao Lili, Liu Zhong, Jin Zhenyu. High-resolution reconstruction of images from an interferometry telescope[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2009, 6(4): 327-333. |
| [4] | Golay M J E. Point array having compact, nonredundant autocorrelations[J]. Journal of the Optical Society of America, 1971, 61(2): 272-273. |
| [5] | 刘丽, 江月松. 综合孔径成像原理与应用[M]. 北京: 国防工业出版社, 2013. |
| [6] | Miller N, Duncan B, Dierking M P. Resolution enhanced sparse aperture imaging[C] // Proceedings of IEEE Aerospace Conference.2006. |
| [7] | Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: from error visibility to structure similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. |


