2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
卫星激光测距(Satellite Laser Ranging,SLR)是现代卫星定轨精度最高的技术之一,因测距精度高,它的观测资料已广泛应用于卫星动力学、空间大地测量、地球动力学和地球物理等研究领域[1]。随着卫星激光测距技术的发展,常规卫星激光测距的单次测距精度已达到亚厘米级[2]。然而,常规激光测距仅适用于携带后向反射器的合作目标,而在轨的空间目标多为非合作目标,如空间碎片等,为了拓展激光测距技术的应用范围,发挥其测距精度高的特点,近年来,空间碎片激光测距技术得到世界上很多国家的重视。目前,已有多个台站成功获取了空间碎片的实测数据。
从已公布的相关资料可知测距精度不低于50 cm。如Stromlo激光测距站利用口径1.8 m的激光发射望远镜探测空间碎片[3],测量精度优于1.5 m[4];Graz测距站,平均数据精度 70 cm[5];上海天文台,测距精度优于80 cm[6, 7];长春人卫站,平均测距精度1 m[8];云南天文台,测距精度50~250 cm[9, 10]。在漫反射激光测距过程中,影响测距精度的因素很多,如计时设备的计时精度,带定比触发的主波信号探测精度,带时间游动补偿的单光子探测器的探测精度等,但大部分仪器对测距精度的影响归算到距离上在毫米量级[1]。在对漫反射激光测距精度研究,这部分误差源的影响可以忽略。空间碎片表面反射符合漫反射特性,这降低了测距过程中的回波强度,为了能够探测到空间碎片的回波信号,需提高激光器的单脉冲能量及工作频率。然而,由于目前激光器研制及加工水平的限制,在满足漫反射激光测距系统对激光器单脉冲能量及工作频率要求的前提下,很难将激光器的脉冲宽度做到百皮秒量级,一般在漫反射激光测距系统使用中的激光器的脉冲宽度在10 ns左右。
本文从卫星激光测距的原理与工作时序出发,在不考虑目标形状对激光脉冲波形的调制作用情況下,数值模拟分析高斯波形的激光脉冲宽度、回波强度对漫反射激光测距精度的影响。针对这一问题的研究,仅有文[11, 12]根据调Q激光脉冲及噪声分布特点,以盖革模式的雪崩光电二极管的探测概率连续分布为依据,求出在门控时域内所有光电子(信号、噪声)触发探测器的以时间为自变量的概率密度函数,通过统计方法,对基于G-APD激光雷达系统的测距精度和测距准确度进行了研究。然而,该分析方法对卫星激光测距系统的精度分析存在一定的偏差,在后续数据处理时,并不是把门控内的所有光电子(信号、噪声)触发探测器的时刻用做最终的数据归算,而是要进行筛选,即对门控内的可识别的回波数据进行选取后,完成后续的数据处理工作。
1 基于C-SPAD的卫星激光测距系统原理被广泛使用在激光测距系统中的单光子探测器C-SPAD是工作在盖革模式下的雪崩光电二极管。当加在雪崩光电二极管探测器上的偏压达到或者超过雪崩电压时,探测器的灵敏度能够达到单光子探测水平,产生的光电子使探测器产生雪崩效应,使得输出电流大幅增加。C-SPAD的卫星激光测距系统原理如图 1。
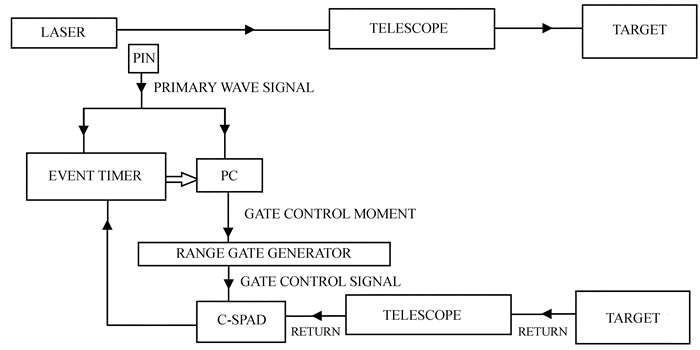
|
| 图 1 C-SPAD的卫星激光测距系统原理图 Fig. 1 Principle of satellite laser ranging system based on C-SPAD |
在测距时,激光经光电二极管(PIN)主波探测器产生主波信号送事件计时器记录下主波时刻tp,同时将该信号送至控制计算机,结合目标轨道预报计算门控时刻,结果送距离门发生器;在回波快到达时刻由距离门发生器产生门控信号给C-SPAD,使其开门探测回波信号[13],在此过程中,无论是噪声还是信号光子触发了探测器都会输出一个探测信号并关闭C-SPAD,并由事件计时器记录C-SPAD探测信号的输出时刻tr;计时器将记录的tp与tr时刻送控制计算机,计算出tp与tr的间隔并将其与目标预报数据做差,将差值形成的点云图进行部分显示,用于实时测距监测[14]。在后续数据处理时,以一定的距离窗口选取点云图中数据密集的区域,剔除噪声异常值,将余下的数据进行归算。
2 C-SPAD卫星激光测距系统的测距精度 2.1 C-SPAD探测器探测概率模型不考虑激光脉冲展宽时,假设回波脉冲的时域分布满足高斯分布,脉冲回波光电子数的时间函数可表示成:
| $ G\left( t \right) = \frac{{{N_{{\rm{sig}}}}}}{{\sqrt {2\pi \sigma } }}\exp \left( { - \frac{{{{\left( {t - {\tau _d}} \right)}^2}}}{{2{\sigma ^2}}}} \right). $ | (1) |
回波脉冲宽度取高斯波形的半高全宽τFWHM,经计算得出:
| $ {\tau _{FWHM}} = 2.354{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 8\sigma . $ | (2) |
| $G\left( t \right) = \frac{{{N_{{\rm{sig}}}}}}{{\sqrt {2\pi } \frac{{{\tau _{FWHM}}}}{{2.354{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 8}}}}\exp \left( { - \frac{{{{\left( {t - {\tau _d}} \right)}^2}}}{{2{{\left( {\frac{{{\tau _{FWHM}}}}{{2.354{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 8}}} \right)}^2}}}} \right). $ | (3) |
对于C-SPAD探测器,其噪声主要来源于互不相关的背景噪声和探测器暗计数噪声,假设二者满足均匀分布,在任意时间段T1到T2产生的噪声平均光电子数满足:
| $ {N_{\rm{n}}} = {n_{\rm{b}}}\eta + {n_{\rm{d}}}, $ | (4) |
根据C-SPAD单光子探测器的探测原理可以导出,开门时刻为0时刻,对于任意时间段 T1到T2的探测概率应该等于在0到T2时间段探测到的情况下,0到T1时间段没有探测的概率即[15]
| $ {P_D}\left( {{T_1},{T_2}} \right) = \exp \left[ { - \int_0^{{T_1}} {f\left( t \right)dt} } \right] - \exp \left[ { - \int_0^{{T_2}} {f\left( t \right)dt} } \right], $ | (5) |
参考云南天文台1.2 m漫反射激光测距系统,假设回波脉冲服从高斯分布且脉冲宽度为10 ns,门宽200 ns,τd为100 ns,此时,在探测器的距离门内不同时隙C-SPAD被触发的概率分布随回波强度变化的关系如图 2。
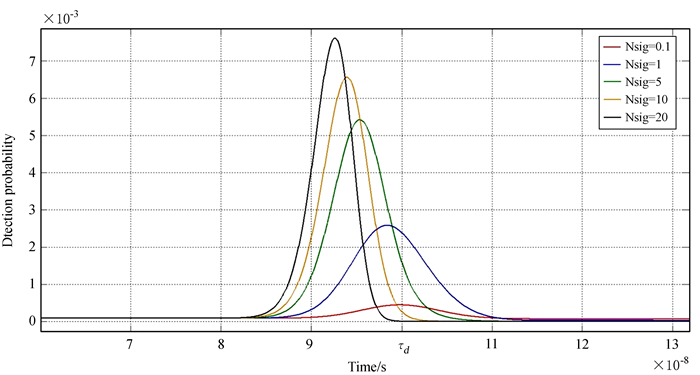
|
| 图 2 C-SPAD在不同时隙被触发的概率分布 Fig. 2 C-SPAD triggered probability distribution in different time bin |
由图 2,当Nsig<<1时,探测器被触发的概率分布的峰值所对应的时刻与τd相近;当Nsig>>1时,由于探测器被输入脉冲前沿的触发概率提高,探测器输出信号的时刻提前于τd的概率也随之增强,且随着回波强度的提高,触发概率所对应的峰值时刻偏离τd越远,此时触发概率分布越集中,从而测距精度有所提高。
在C-SPAD探测过程中,探测器在距离门内被噪声触发的概率随时间递减,在回波信号出现以前探测概率分布形成一个概率极小值pvol,随着回波信号的出现逐渐形成概率相对极大值ppeak,当二者比值相差越大时,回波信号可别度越高[15],更有利于在大量噪声中提取回波信号。在后续的模拟计算中,选取回波信号所对应的触发概率高于Pvol时为回波信号的可识别区域,如图 3,选取的时间区域为[T3,T4]。
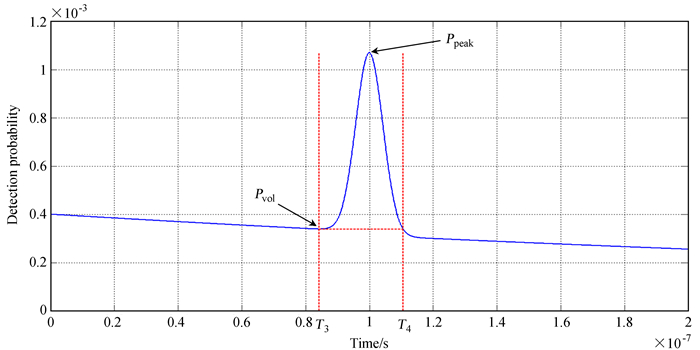
|
| 图 3 回波信号的可识别区域示意图 Fig. 3 Areas of echo signal that can be discerned |
将距离门时间段共划分N个时隙,每个时间间隔为Δt,将第i个时隙的探测概率记为PD(i),设时间T3处在第K个时间隙内,T4在第M个时间隙内,则对于选取区域[T3,T4],可将该区域内的各时隙探测概率写为
| $ {P_{D1}}\left( j \right) = {P_D}\left( {K + j} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {j = 0,1, \cdots ,M - K} \right). $ | (6) |
| $ {P_{D2}}\left( j \right) = \frac{{{P_{D1}}\left( j \right)}}{{\sum\limits_{i = 0}^{M - K} {{P_{D1}}\left( i \right)} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {j = 0,1, \cdots ,M - K} \right), $ | (7) |
| $ \sum\limits_{j = 0}^{M - K} {{P_{D2}}\left( j \right)} = 1. $ | (8) |
| $ \overline {{t_d}} = \sum\limits_{j = 0}^{M - K} {{P_{D2}}\left( j \right)} t\left( {K + j} \right), $ | (9) |
| $ {R_{{\rm{ao}}}} = \frac{{\left( {\overline {{t_d}} - {\tau _d}} \right)}}{2}. $ | (10) |
| $ {R_{{\rm{po}}}} = \frac{{\sqrt {\sum\limits_{j = 0}^{M - K} {{P_{D2}}\left( j \right)} t{{\left( {K + j} \right)}^2} - {{\left( {\overline {{t_d}} } \right)}^2}} }}{2}. $ | (11) |
图 4显示了在不同回波强度和脉冲宽度时的测距精度。由图 4可知,激光脉冲宽度是影响测距精度的重要参量,在相同回波强度时,脉冲宽度越窄,测距精度越高,主要是因为脉冲宽度越窄,光子能量越集中,则光子的时间分布处在更小范围,因此测距精度越高;在相同脉宽情况下,随着回波信号强度的增强,回波脉冲前沿触发C-SPAD的概率提高,导致测距精度随回波强度的增加而提高;在脉冲宽度为10 ns、噪声50 kHz及回波强度小于1个光电子时,由脉冲宽度引起的测距精度不大于2.5 ns,等效到距离上小于75 cm,根据云南天文台公布的漫反射激光测距精度50~250 cm[9, 10]可知,漫反射激光测距系统的测量数据包含了漫反射目标在观测方向的深度信息,下一步工作将对这一问题进行讨论。当回波强度大于5个光电子时,由脉冲宽度引起的测距数据的精度优于1.6 ns。
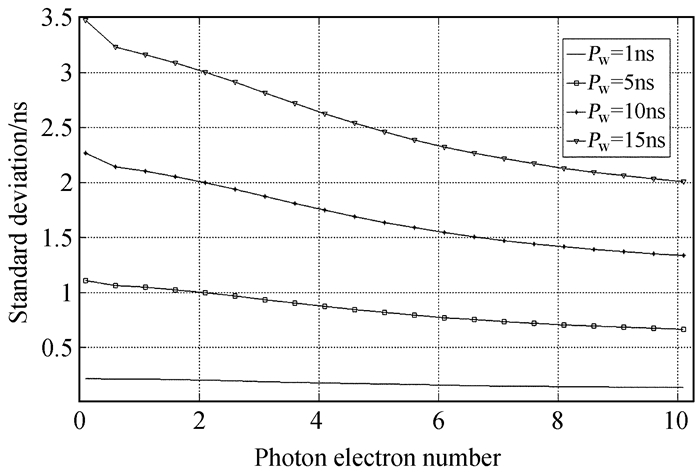
|
| 图 4 测距精度与回波强度和脉冲宽度的关系 Fig. 4 Relationship among ranging precision,echo intensity and pulse width |
图 5为测距准确度与回波强度的关系,由图 5,在相同回波强度下,测距数据准确度随脉冲宽度的增宽而降低;在相同脉冲宽度的情况下,回波信号强度越强,测距数据的准确度越低,这是因为当回波强度增强,脉冲前沿触发探测器的概率提高,导致探测器触发时刻提前于目标在门控内的时刻,当取激光脉冲宽度为10 ns时,回波强度为10个光电子,此时测距准确度约为-6.3 ns。
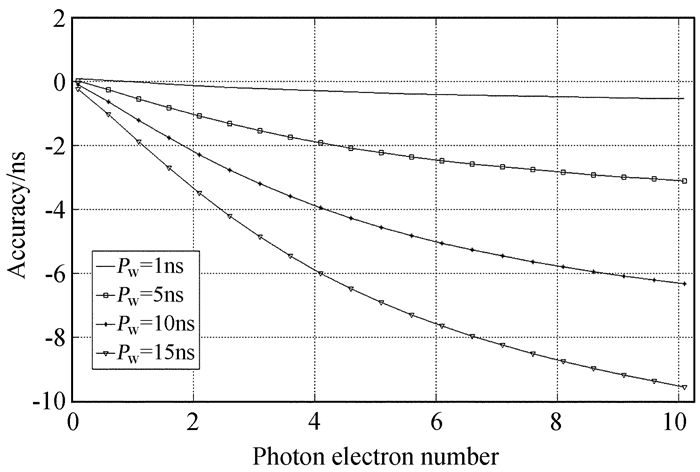
|
| 图 5 测距准确度与回波强度和脉冲宽度的关系 Fig. 5 Relationship among ranging accuracy,echo intensity and pulse width |
不同回波强度导致测距准确度的偏差可视为测距系统的系统误差,通过对已知距离的地面靶标进行强回波时的系统延时标定,并在实测中实时监测回波信号强度,使其与地靶标定时的回波强度相近,才可以同时提高测距精度与测距准确度。
图 6、图 7为激光脉冲的半高全宽为10 ns、噪声强度为10 kHz、50 kHz、100 kHz、500 kHz时,不同回波强度与测距精度和测距准确度的关系图。由图 6可知,噪声强度低时的测距精度相对于强噪声时的测距精度高,即数据弥散度低;在回波强度为单光子量级、噪声强度为10 kHz和500 kHz时,测距精度差值为0.12 ns。由图 7可知,随着噪声强度的增加,测距准确度略微降低;在回波强度为单光子量级、噪声强度为10 kHz和500 kHz时,测距准确度的差值为0.145 ns。
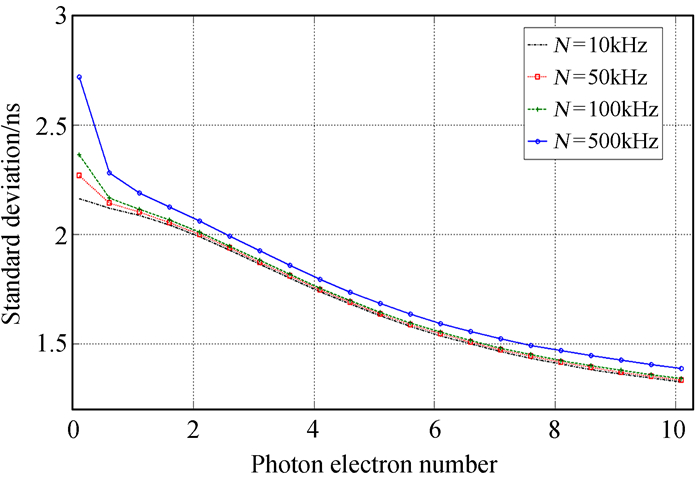
|
| 图 6 测距精度与噪声强度的关系 Fig. 6 Ranging precision distribution under different noise intensity |
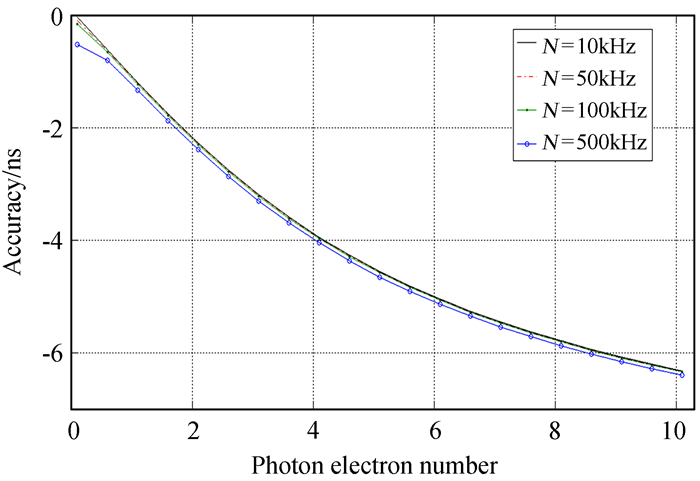
|
| 图 7 测距准确度与噪声强度的关系 Fig. 7 Ranging accuracy distribution under different noise intensity |
在不考虑漫反射目标的形状时,相对于回波强度和激光脉冲宽度,噪声强度对测距精度和测距准确度的影响不大;减小激光脉冲宽度能够有效提高测距精度和准确度;当激光脉冲宽度不能减小时,单独提高激光发射能量虽能提高测距精度,但测距准确度却降低,此时需要对已知距离的地面靶标进行不同回波强度时的系统延时标定,并在实测中监测回波信号强度,使其与地靶标定时的回波强度相近,才可以在不降低测距准确度的情况下提高测距精度。
| [1] | 叶叔华, 黄珹. 天文地球动力学[M]. 济南: 山东科学技术出版社, 2000. |
| [2] | 张忠萍, 杨福民. 卫星激光测距的新进展[J]. 天文学进展, 2001, 19(2): 283-288. Zhang Zhongping, Yang Fumin. The progress in Satellite Laser Ranging[J]. Progress in Astronomy, 2001, 19(2): 283-288. |
| [3] | Greene B. Laser tracking of space debris[R]// Proceedings of 13th International Workshop on Laser Ranging Instrumentation. 2002. |
| [4] | Sang J, Smith C. An analysis of observations from EOS space debris tracking system[C]// Australian Space Science Conference 2011, September 26-29, Canberra, Australia. 2011. |
| [5] | Kirchner G, Koidl F, Friederich F, et al. Laser measurements to space debris from Graz SLR station[J]. Advance in Space Research, 2013, 51(1): 21-24. |
| [6] | Yang Fumin, Zhang Zhongping, Chen Juping, et al. Preliminary results of laser ranging to un-cooperative targets at Shanghai SLR station[C]// Proceedings of 16th International Workshop on Laser Ranging Instrumentation. 2008: 695-699. |
| [7] | Zhang Zhongping, Yang Fumin, Zhang Haifeng, et al. The use of laser ranging to measure space debris[J]. Research in Astronomy and Astrophysics, 2012, 12(2): 212-218. |
| [8] | Liu Chengzhi, Sun Jiannan, Dong Xue, et al. Laser ranging on space debris with the Changchun SLR station[C]// Proceedings of 19th International Workshop on Laser Ranging Instrumentation. 2014. |
| [9] | 李语强, 李祝莲, 伏红林, 等. 空间碎片漫反射激光测距试验[J]. 中国激光, 2011, 38(9): 0908001-1-0908001-5. Li Yuqiang, Li Zhulian, Fu Honglin, et al. Experimentation of diffuse reflection laser ranging of space debris[J]. Chinese Journal of Lasers, 2011, 38(9): 0908001-1-0908001-5. |
| [10] | 李祝莲, 李语强, 伏红林, 等. 10赫兹漫反射激光测距控制系统的设计与实现[J]. 天文研究与技术——国家天文台台刊, 2012, 9(3): 302-307. Li Zhulian, Li Yuqiang, Fu Honglin, et al. Design and realization of a 10Hz diffuse- reflection laser ranging control system[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2012, 9(3): 302-307. |
| [11] | Wang Fei, Zhao Yuan, Zhang Yu, et al. Range accuracy limitation of pulse ranging systems based on Geiger mode single-photon detectors[J]. Applied Optics, 2010, 49(29): 5561-5566. |
| [12] | 王飞, 赵远, 张宇, 等. 激光脉冲强度对于盖革模式单光子探测测距精度影响的理论研究[J]. 光学学报, 2010, 30(10): 2771-2775. Wang Fei, Zhao Yuan, Zhang Yu, et al. Theoretical analysis of influence of laser signal strength on range precision in single photon ranging[J]. Acta Optica Sinica, 2010, 30(10): 2771-2775. |
| [13] | 姜崇国, 何妙婵, 郑向明. 可门控单光子探测器在天文观测中的应用[J]. 光电子技术与信息, 2001, 14(4): 35-38. Jiang Chongguo, He Miaochan. The application of the gateable single photon detectors in astronomical observation[J]. Optical-Electron Technology and Information, 2001, 14(4): 35-38. |
| [14] | 郑向明, 李祝莲, 伏红林, 等. 云台1.2 m望远镜共光路千赫兹卫星激光测距系统[J]. 光学学报, 2011, 31(5): 0512002-1-0512002-5. ZhengXiangming, Li Zhulian, Fu Honglin, et al. 1.2m telescope satellite co-optical path kHz laser ranging system[J]. Acta Optica Sinica, 2011, 31(5): 0512002-1-0512002-5. |
| [15] | 翟东升, 汤儒峰, 黄凯, 等. 基于G-APD阵列的卫星激光测距系统的探测性能分析[J] . 中国激光, 2015, 42(6): 0608007-1-0608007-7. Zhai Dongsheng, Tang Rufeng, Huang kai, et al. Analysis on detection performance of satellite laser ranging based on Geiger mode APD arrays[J]. Chinese Journal of Lasers, 2015, 42(6): 0608007-1-0608007-7. |



