数据融合(也叫信息融合)的概念始于20世纪70年代,至80年代其技术取得了一定的进步和发展,到90年代不少数据融合技术的研究成果已得到实际应用,取得了理想的效果^[1]。数据融合的主要原理是用多个传感器(同质或异质的)对同一对象进行描述,得到该对象的多源观测数据,将这些数据进行集成,以获得对被控对象的更好的理解^[2]。

多传感器信息融合技术是近几年发展起来的一门实践应用技术,是针对一个系统使用多种传感器这一特定问题而展开的一种关于数据处理的技术^[3]。对于多传感器系统,由于信息的多样化和复杂性,因此,信息融合方法的基本要求是具有强大的处理能力,以及较高的计算速度和精度。人工智能的发展使信息融合技术走向智能化、集成化。

数据融合的目的是合并或合成多个数据集,成为一个完整的性能更好的数据集。数据融合技术的实现,关键在于融合算法^{[4, 5]}。在融合求解过程中,不是仅仅把数据或解集简单地直接组合,这样做效果不会很明显,甚至最后得到的结果更差。为了能够得到良好的融合效果,应该分析各组方程解或多组数据集序列的特征。比如一些数据序列的随机误差较小但偏差较大;一些数据的随机误差较大但偏差较小^{[6, 7]}。这样就可以将随机误差较小的数据序列的相对变化量通过一定的方法融合到随机误差较大的数据序列中,能获得随机误差较小且偏差也较小的数据序列。本文基于广义延拓插值外推法^[8]提出了一种求解一类特定的关联群方程组的多个离散数据集或最优融合估计集的方法,称之为广义融合方法。经过实验证明,该方法实用性好,数据平稳性好,外推稳定度高,已应用于卫星导航定位数据处理领域。

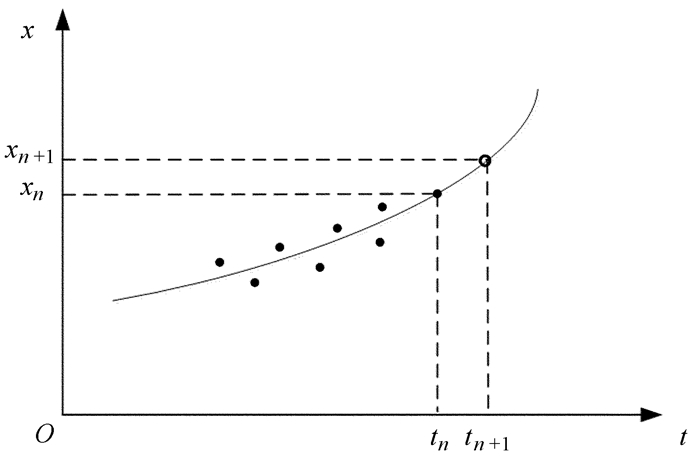
1 广义延拓插值外推法

广义融合是基于广义延拓插值外推法提出的,因此,先介绍广义延拓插值外推法。广义延拓插值外推法的基本设计理念是^[9]:分段实施最小二乘逼近,在每段的端点处采用插值处理,在段内采用拟合处理,段内拟合逼近处理时,用邻近延拓域里的数据进行辅助拟合处理,从而使逼近多项式在定义域内的逼近精度升高;当分段连接后,在连接端点处过渡平滑,在整域上逼近精度比较好。广义延拓最小二乘逼近方法的外推模型兼融了插值和拟合两大功能,具有极好的逼近精度。外推示意图见图 1。

假设已知历元t_n时刻的最优估计值${{hat x}_n}$和t_n之前的数据值(${{\hat x}_1},{{\hat x}_2}, \cdots ,{{\hat x}_{n - 1}}$),求下一时刻t_n+1的值x_n+1,这是一个典型的数据外推问题,可建立如下广义延拓插值外推模型^[1]:

$ \left\{ \begin{array}{l} \min I\left( {{a_1},{a_2},{a_3}} \right) = \sum\limits_{i = m}^{n - 1} {{{\left[ {{a_1} + {a_2}{t_i} + {a_3}t_i^2 - {x_i}} \right]}^2}} \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_1} + {a_2}{t_n} + {a_3}t_n^2 = {x_n} \end{array} \right., $

(1)

其中,minI(a₁、a₂、a₃)为逼近残差极小化目标函数;a₁、a₂、a₃为待求的系数;s.t.示意约束条件。求解模型(1),可以优化获得广义延拓逼近多项式的待求系数a₁、a₂、a₃;代入(2)式:

$x\left( {{t_j}} \right) = {a_1} + {a_2}{t_i} + {a_3}t_i^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = n + 1,n + 2, \cdots } \right), $

(2)

便可以外推求解得到t_n+1历元的估计值${{\hat x}_{n + 1}}$。

2 广义融合方法的数学模型及其求解方法 2.1 广义融合方法数学模型的建立

广义融合求解模型借鉴了广义延拓插值外推公式,即在t_n历元时,选用多项式a₁+a₂t_n+a₃t_n²作为逼近函数。逼近时选用一段历元内的数据,其中把已获得的先验最优估计值(起始时由于没有先验最优估计值,可以先用测量值代替)作拟合逼近处理;选用当前待求历元的广义状态量的预估值与测量值的最优加权组合逼近形式作为插值约束锁定点;以逼近多项式系数a₁、a₂、a₃和权系数k₁、k₂等为优化求解变量;以逼近函数多项式系数a₁、a₂、a₃,权系数k₁、k₂以及广义状态量等待求量的区间数作为变量取值约束条件。这些约束条件把解限制在一定的范围之内,从而提高解的精度。

构造广义融合最优化求解模型,求a₁、a₂、a₃,使满足:

$ \left\{ \begin{array}{l} \min {I_1}\left( {{a_1},{a_2},{a_3}} \right) = \sum\limits_{i = n - m}^{n - 2} {{{\left[ {{a_1} + {a_2}{t_i} + {a_3}t_i^2 - {{\hat x}_i}} \right]}^2}} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {k_1}{\left[ {{a_1} + {a_2}{t_n} + {a_3}t_n^2 - {{\tilde x}_n}} \right]^2} + {k_2}{\left[ {{a_1} + {a_2}{t_n} + {a_3}t_n^2 - {x_n}} \right]^2}\\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_1} + {a_2}{t_{n - 1}} + {a_3}t_{n - 1}^2 = {{\hat x}_{n - 1}};{k_1} + {k_2} = 1\\ {a_1} \subseteq {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_1},{a_2} \subseteq {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_2},{a_3} \subseteq {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_3} \end{array} \right., $

(3)

其中,I₁(a₁,a₂,a₃)为待优化的目标函数,优化的目标函数既可以是线性关系也可以是非线性关系,若是非线性关系,则广义融合方法直接采用非线性求解算法求解;${{\hat x}_i}$为状态量的测量值;${{\tilde x}_i}$为状态量的最优估计值;x_i为由低阶状态量递推获得的状态量的预估值;i为历元序号;k₁、k₂为权系数,它们的取值大小影响它们各自的残差对目标函数的贡献,权值的分配在本文后面作详细的 介绍;x_n为t_n历元时状态量的测量值;${{\tilde x}_n}$为t_n历元时状态量的递推预估值;${{\tilde x}_{n - 1}}$为t_n-1历元时状态量的最优估计值;${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_1}$、 ${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_2}$、${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }_3}$为可行区间变量a₁、a₂、a₃的约束区间数,${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _1} = \left[ {{{\underline a }_1},{{\bar a}_1}} \right],{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _2} = \left[ {{{\underline a }_2},{{\bar a}_2}} \right],{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _3} = \left[ {{{\underline a }_3},{{\bar a}_3}} \right]$。广义融合模型中可以包含非线性状态方程、非线性约束方程以及其它非线性测量方程,这能够扩大应用范围,增加方程的冗余性和连续性,提高求解精度。

2.2 广义融合方法的求解步骤 2.2.1 求解状态量值

建立残差极小化优化模型并加约束方程,如下式:

$ \begin{array}{*{20}{c}} {\min I\left( {{x_n}} \right) = \sum\limits_{i = 1}^n {{{\left( {F\left( {{x_i}} \right) - {Y_i}} \right)}^2}} }\\ {s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f\left( {{x_n}} \right) = 0} \end{array}, $

(4)

其中,F(x_i)为状态量关系式,多数情况下为非线性函数关系,可以采用非线性算法直接求解;x_i为函数状态变量;Y_i为测量量;i为历元序号;n为当前历元数;f(x_n)为约束函数关系式。(4)式可以采用非线性算法求解,如单纯形法等。通过搜索、比较等步骤,使目标函数值不断逼近最优点。求解方法在优化过程中不受方程个数的限制,并且具有简单直观、适应性强、应用范围广、解决速度快等特点。

2.2.2 求解状态量的预估值${{\tilde x}_n}$

利用外推得到的状态方程的高阶状态量可以提高解的精度和相关性,低阶状态量可以是与状态量 相关的导数值或微分值。当求解t_n历元时刻状态量的预估值${{\tilde x}_n}$时,由于已经得到t_n-1历元时刻状态量的最优估计值${{\hat x}_{n - 1}}$(在初始阶段的融合,初始状态最优估计值是未知的,可用前几个时刻状态的测量值代替),可以通过公式:

$ {{\tilde x}_n} = {{\hat x}_{n - 1}} + {{\dot x}_n}\Delta t + \frac{1}{2}{{\ddot x}_n}{\Delta ^2} + \cdots , $

(5)

递推获得t_n历元时刻状态量的预估计值${{\tilde x}_n}$。(5)式中${{\tilde x}_n}$为t_n历元时刻状态量的预估值;${{\hat x}_{n - 1}}$为t_n-1时刻状态量的最优估计值;${{\dot x}_n}$为t_n历元时刻状态量的一阶导数;Δt为相邻历元之间的时间间隔;${{\ddot x}_n}$为t_n历元时刻状态量的二阶导数。

2.2.3 求解状态量的最优估计值${{\hat x}_n}$

经上述步骤,已经求得状态量值和状态量的预估值,t_n历元时刻直接求解获得的状态量x_n和t_n历元时刻获得的状态量的预估值${{\tilde x}_n}$,现在需要把它们组合起来,求得t_n历元时刻状态量的最优估计值${{\hat x}_n}$,即

${{\hat x}_n} = {a_1} + {a_2}{t_n} + {a_3}t_n^2, $

(6)

其中,a₁、 a₂、 a₃可以由广义融合最优化求解模型((3)式)采用直接法等优化算法求解得到。将得到的a₁、 a₂、 a₃代入(6)式可得到t_n历元时刻状态量的最优估计值${{hat x}_n}$。

2.2.4 求解一组优化的最优估计值解 对上述4个步骤不断进行迭代、递推,直到结束,就能够得到一组优化的最优估计值解${{\hat x}_i}$,i=1,2,3 … k_end。

3 广义融合模型之中权值分析

在广义融合方法数学模型((3)式)中a₁+a₂t_n+a₃t_n²-x_n表示逼近函数与状态量之间的残差; a₁+a₂t_n+a₃t_n²-${{\tilde x}_n}$表示逼近函数与状态量的预估值之间的残差。它们的权系数k₁、k₂的取值大小会影响它们各自的残差对目标函数的贡献,所以权值的选择极为重要。故在确定权系数之前要分析状态 量的预估值${{\tilde x}_n}$、状态量的测量值${{\tilde x}_n}$与逼近函数之间的残差大小比例关系;在融合数据时,要考虑被融合数据自身的精度及误差特性等诸多因素。通过改变k₁、k₂的大小可以调控广义融合最优估计值与状态量及预估值的靠近程度。

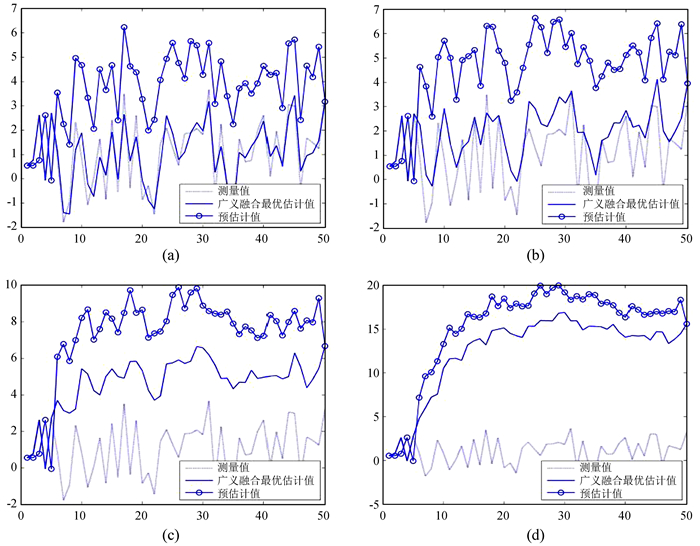
用仿真验证方法的可行性,即生成两组数据:一组数据随机误差较大但偏移较小(随机误差-3-3,偏差为1);另一组随机误差较小但有较大的偏移(随机误差-1-1,偏差为3)。数据生成后代入广义融合求解模型,选取不同的4对权值进行组合分析,所得结果如图 2。

从图 2(a)、(b)、 (c)、 (d) 4幅图可以看出:当k₁逐渐减小而k₂逐渐增大时,状态量的最优估计值开始远离状态测量值向预估值逼近;随着k₁越来越小,k₂越来越大,这种现象更加明显。在数据处理过程中,如果有一组数据序列的某些测量量发生突跳导致数据不准确时,便可以通过改变权值组合来降低这些突跳数据对获取最优估计值的贡献,使获得的最优估计值更加平稳。

4 广义融合方法在卫星导航中的应用及仿真与实测分析 4.1 广义融合在卫星导航中的应用

以卫星定位导航为例说明采用广义融合方法的实用性:卫星导航定位解算出用户的位置坐标为x 、y、z3个方向,本文只对一个方向的用户位置作详细分析,其余两个方向使用相同方法修正即可获得用户位置的完整坐标。

4.1.1 获得t_m时刻位置最优估计值解${{\hat x}_m}$和相应时刻的速度${{\hat v}_m}$

将从初始时刻到t_m历元时刻接收机的位置量设为x_i(i=1,2,…,m)。通过对t_m历元时刻以前的位置测量量采用分段最小二乘拟合的方法(5个历元时刻点做一次拟合)对位置测量量进行处理,用处理后通过逼近多项式(6)获得的t_m时刻的值,作为t_m时刻位置的最优估计值解${{\hat x}_m}$^[10]。由于在导航定位中速度的测量值精确度较高,初始时刻的最优速度值及之后各时刻的最优速度值都直接选用对应时刻的速度测量值即可。

4.1.2 获取t_m+1时刻位置量的预估值${{\tilde x}_{m + 1}}$

由第1步已经得到了t_m时刻位置的最优估计值解${{\hat x}_m}$和相应时刻速度的最优值${{\hat v}_m}$,利用(5)式 解算出t_m+1时刻位置量的预估值x_m+1。(5)式中${{\dot x}_n}$为t_n历元时刻状态量的一阶导数即t_n时刻的速度值;${{\ddot x}_n}$为t_n历元时刻状态量的二阶导数即加速度值,加速度本文暂不考虑。

4.1.3 获得t_m+1时刻最优估计值解${{\hat x}_{m + 1}}$

通过上述步骤,已经得到t_m+1时刻位置量的预估值,相应时刻位置量的测量值可以通过测量数据直接获得。因为实际的测量值会因为误差等因素导致最终结果不精确,所以本文在测量值与预估值之间添加一个阈值。当两者之间的绝对差值超过这个阈值时,便认为测量值已经发生了跳变,此时(3)式中的权值组合k₁≈0、k₂≈1,使最优估计值的解向预估值方向逼近;当两者之间绝对差值没有超过阈值时,认为测量数据在误差范围之内,就要选择合适的权值组合,再代入(3)式,组合求解获得最优估计值${{\hat x}_{m + 1}}$。

4.1.4 获得经优化的一组最优估计值解

上述第2、第3步不断迭代、递推、融合就能获得一组优化的最优估计值解${{\hat x}_{m + 1}},{{\hat x}_{m + 2}}, \cdots ,{{\hat x}_{{\rm{end}}}}$。

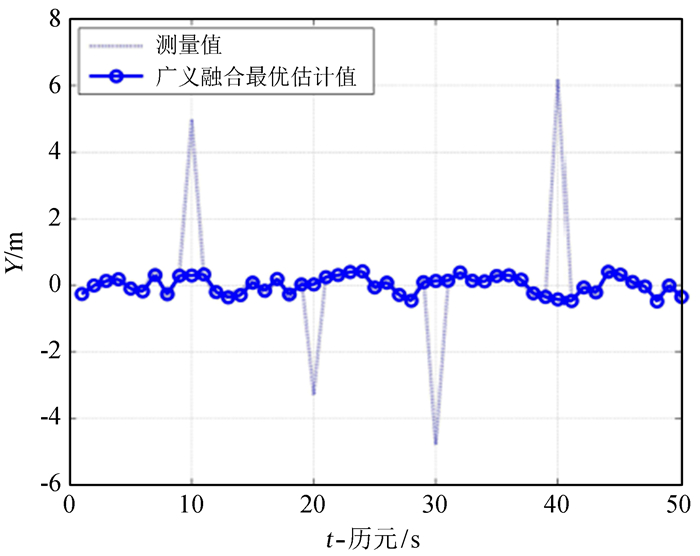
4.2 仿真 4.2.1 广义融合对突跳数据的修正

卫星定位系统的精度主要取决于两方面: 一是观测卫星在空间的分布情况,通常称为卫星分布几何衰减因子; 二是各观测量的精度^[11]。大气层干扰、对流层延迟改正后的残差、星历误差及多路径效应等影响导致最后的测量数据产生偏差或是突跳,而广义融合方法能够很好地修正这些误差数据。现生成一组随机误差在(-0.5-0.5)的数据,分别在第10、20、30、40 4个点处加上较大的偏移量构成突跳点,然后用广义融合方法对这组数据进行处理,仿真结果如图 3。

由图 3可以看出,广义融合法对4个突跳点的数据都做了实时修正,其结果不但在没有发生突跳的部分很好地遵循了原始测量值的变化规律,而在有突跳的时段,也能有效排除突跳的影响。

4.2.2 最小二乘拟合法与广义融合法对误差数据处理对比

在卫星数目多于4颗,各测量值之间相互独立且符合高斯正态分布的情况下,采用最小二乘算法解算接收机的三维坐标是最经典的办法。因为最小二乘算法能使各观测伪距之间的残差平方和最小,从而使获得的估计值解达到最优。但是多路径效应等因素产生的误差却时刻影响其定位精度,这导致各实际测量值之间并不是相互独立,甚至有些情况下不符合正态分布,这时若仍采用最小二乘算法就很难保证最后能获得最优估计值解^[12],而广义融合法在此种情况下依然适用。

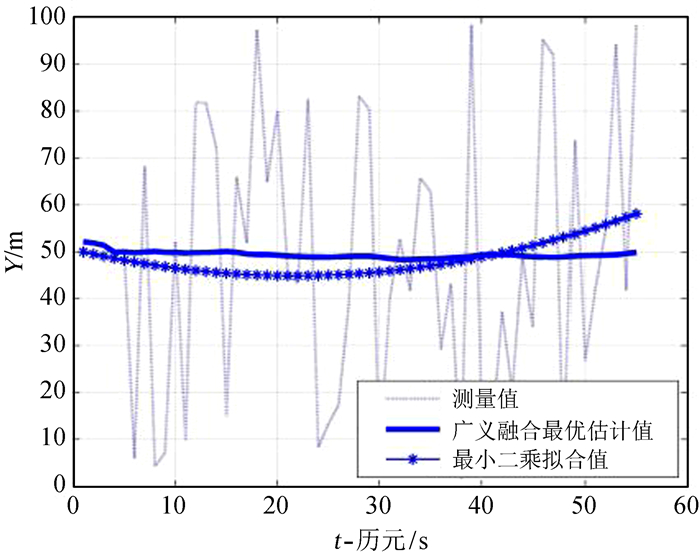
下面通过仿真实验验证此方法的有效性。令测量值的理论值为50,这时在理论值的基础上加噪声生成一组带有随机误差的数据,作为测量仿真计算数据,为了便于体现广义融合法的优越性,分别用广义融合法和最小二乘算法对这组数据进行处理,修正后的效果如图 4。

经计算,得到最小二乘拟合值的标准差为σ=3.626 396 349 003 966,广义融合最优估计值的标准差为σ=0.758 068 193 045 756,广义融合法稳定程度要比最小二乘拟合法提高大约79%(图 4);而且广义融合法的偏差也较小,误差数据的修正值更加靠近理论值。

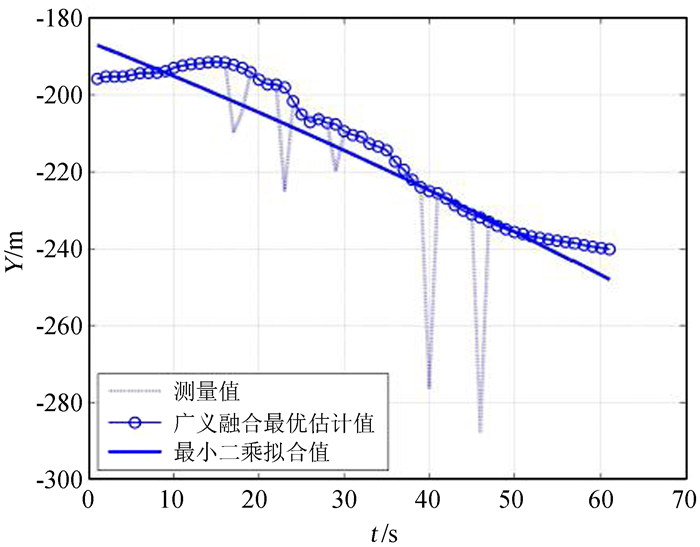
4.2.3 实测数据分析

(1) 2015年5月11日在中国科学院国家天文台用中科微ATGM332D卫星定位芯片的接收机做动态测试。从最终获取的接收机三维坐标中截取Y方向上一段带有明显突跳的原始定位数据和对应时刻的原始速度值,分别用广义融合法和最小二乘拟合法对其进行处理,结果如图 5。

由图 5可以看出最小二乘拟合法对某些突跳点并没有很好的修复作用,只是在少数点处遵循了原始数据的变化规律,但是整体数据偏离了实测数据;而广义融合法能实时修正原始数据中的坏数据,并且在没有发生突跳的部分很好地跟随原始数据的运动轨迹。

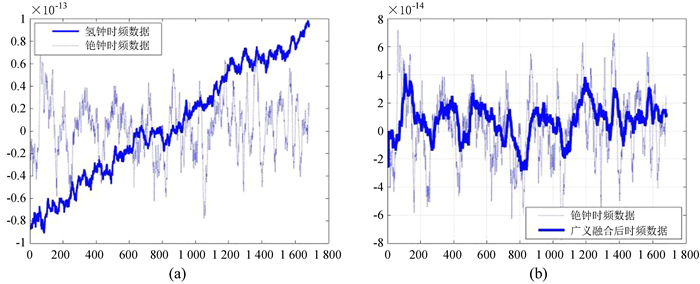
(2) 当代社会对时频基准的要求越来越高,氢原子钟、铯原子钟等多种高精度时频基准已被相继研发出来。然而还可以通过另外一种方法获得更高精度和稳定度的时频基准,那就是组合处理和精细加工原子钟组的输出数据,获得性能更优良的时频输出数据。本文把氢原子钟与铯原子钟的输出数据用广义融合法融合起来。图 6(a)显示了铯原子钟与氢原子钟输出的频率数据变化图,通过对比可以发现铯原子钟频率的随机误差偏大,但长期稳定度很好;而氢原子钟则不同,它随机误差的幅度很小,但是随着时间的增长其频率出现很明显的漂移。广义融合法能把这两种原子钟的频率特性的优势组合起来,从而获得随机误差小并且长期稳定度好的时频基准。用这一方法对国家授时中心的铯原子钟和氢原子钟输出的时频数据进行融合处理,用氢钟时频的变化率修正铯钟的时频输出,处理结果见图 6(b)。

5 结 论

本文针对卫星导航定位数据中出现的坏数据,尤其是突跳数据的修正,在广义延拓插值外推法的基础上提出了一种新的数据融合方法——广义融合法。通过仿真和实测数据分析,与最小二乘算法进行对比后得出:广义融合法较最小二乘拟合法更能够修复定位数据中产生的突跳数据;广义融合法比最小二乘拟合法对数据的处理可靠性更高;广义融合法实用性好,数据平稳性好,外推稳定度高,有望成为一种新的解决数据融合问题的普适求解方法。