2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijng 100049, China
时域脉冲雷达具备快速、无损、高分辨率等特点,是一种应用广泛的浅层电磁探测手段。在地球探测中,时域脉冲雷达广泛应用于工程与环境地球物理勘查、工程质量检测、水文地质检测、基地考察等领域[1, 2];嫦娥三号月球车搭载的测月雷达正是基于时域脉冲机制,其科学目标为探测月壤厚度及次表层的结构特性[3],基于嫦娥三号的雷达数据处理也取得了一些初步的结果[4, 5, 6]。该雷达工作原理为发射天线发射高频脉冲电磁波,电磁波在传播过程中,由于地下介质存在电性参数差异,会对电磁波的振幅、波形和频率等特性产生影响,通过分析接收天线接收的回波信号推断地下介质结构以及介质的介电特性。
雷达究竟能探测多深,需探测的地下目标是否在雷达系统的有效测距范围之内,在雷达数据中发现的特征信息是否在雷达有效数据范围之内,这是实际工程中必须考虑的一个重要问题[7]。传统的计算方法[8, 9, 10],大多需要预估地下的分层结构以及各分层介质的物理特性,然后结合经典的雷达传输方程对雷达的探测深度进行估计。由于传统探测深度的计算方法需要做先验性假设,没有结合雷达的探测数据,所以只能给出一个理论的估计值。本文提出了一种基于相关系数法雷达极限探测深度的计算方法,该方法不需要对地下介质进行假设,直接从雷达实测数据的角度出发,通过数据间的相关性,给出雷达的极限探测深度。文中对于相关系数法给出了两种具体的计算方法,第1种为子波法,该方法利用雷达发射子波与雷达数据进行相关计算,得到相关系数矩阵,在相关系数矩阵中寻找雷达的极限探测深度;第2种为道相关法,该方法不需要子波,利用相邻道之间的相关性得到相关系数矩阵,在相关系数矩阵中寻找雷达的极限探测深度。
需要指出,基于相关系数法确定的极限探测深度为雷达实测数据中最后一个有用回波信号(强度大于噪声)与噪声的分界位置,在该位置以下,信号成分以噪声为主,即使存在有用信号,也淹没在噪声之中。对于有用信号(强度小于噪声)隐藏在噪声中的情形,有用信号的相关性已经被噪声破坏,采用该方法无法提取,该情形不属于本文的研究内容。另外,有些学者提出结合有效的数据处理方法[11, 12, 13],也可以对弱信号、薄层进行提取,但是很多时候需要信号满足一些特定的约束条件。
本文详细介绍了两种计算方法的理论基础及计算步骤,并通过模型仿真验证和对比了两种计算方法的有效性,并对仿真结果进行了分析和讨论。
1 相关系数法本节介绍两种基于相关系数对雷达极限探测深度进行计算的方法,子波法和道相关法。子波法在计算时需要先对子波进行测量和估计,而道相关法不需要子波,直接利用实测数据。
1.1 子波法子波法计算雷达探测深度的理论基础是当利用雷达子波与单道雷达数据进行滑动相关时,真实的反射信号与子波存在高相关性,噪声信号与子波进行相关运算时相关性较低,在相关矩阵中,找到最后一个高相关信号的位置就是雷达的极限探测深度。
子波的获取可以用模拟仿真和实际测量两种方法。结合软件模拟仿真时,首先搭建仿真模型,将发射天线与接收天线置于自由空间,固定好天线间隔,模型的边界采用吸收边界,发射脉冲选用雷克子波,可以把接收天线接收的波形作为子波。实际测量时,可以选在微波暗室或者空旷的场地,尽量保证周边没有反射介质,同样将接收天线接收的波形作为子波;同时也可以在获取实测数据后,采用子波提取法[14]在实测雷达数据中提取子波。
已知,子波wlet长度为n,实测雷达数据data共有m道数据,每道数据有n_data个采样点;利用子波法进行探测深度计算的具体步骤为
(1) 确定雷达数据中每个采样点对应的处理区间xi,j,区间大小与子波宽度一致;
| $ {x_{i,j}} = \left\{ \begin{array}{l} data\left( {1:n,j} \right),i < \left( {n\_wlet - 1} \right)/2\\ data\left( {n\_data - n + 1:n\_data,j} \right),i > n\_data - \left( {n - 1} \right)/2,\\ data\left( {i - \left( {n - 1} \right)/2:i + \left( {n - 1} \right)/2,j} \right),else \end{array} \right. $ | (1) |
(2) 计算子波均值wlet'以及每个采样点对应采样区间的均值xi,j':
| $ wlet' = \frac{1}{n}\sum\limits_{i = 1}^n {wle{t_i}} ,{x_{i,j}}' = \frac{1}{n}\sum\limits_{i = 1}^n {{x_{i,j}}} . $ | (2) |
(3) 将子波与采样点处理区间进行相关计算得到相关系数,c(i,j)为第j道数据、第i点的相关系数值:
| $ c\left( {i,j} \right) = \frac{{\sum\limits_{i = 1}^n {\left( {{x_{i,j}} - {x_{i,j}}'} \right)\left( {wle{t_i} - wlet'} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {\left( {{x_{i,j}} - {x_{i,j}}'} \right)\left( {wle{t_i} - wlet'} \right)} } }}. $ | (3) |
(4) 遍历该道数据所有采样点以及所有雷达数据道,得到相关系数矩阵C。
(5) 在相关系数矩阵的每列中找到最后一个高相关的脉冲的位置,确定雷达极限探测深度。
1.2 道相关法道相关法与子波法不同,在利用道相关进行探地雷达深度估计时,不需要提取雷达子波,仅依据雷达实测数据,考虑到雷达行进的速度较慢,相邻两道对应地下的介质结构相似,所以有效的反射信号在雷达相邻道之间具有较高的相关性,而噪声为随机的,在相邻道之间的相关性较低,所以道相关法的理论基础是利用雷达数据中有用反射信号在雷达相邻道之间具有的高相关性以及噪声在相邻道之间的弱相关性来确定有用信号与噪声的分界位置,即可得到雷达极限探测深度。
在利用道相关法进行计算时,要设定每个采样点的处理区间,通常情况下,区间应大于一个子波宽度;然后与子波法相同,采用滑动的计算方法,得到每个采样点的相关系数值。
道相关法的具体计算步骤如下:
(1) 确定每个采样点的相关区间,通常情况下,区间大小应大于一个子波的宽度;
| $ {x_{i,j}} = \left\{ \begin{array}{l} data\left( {1:n,j} \right),i < \left( {n - 1} \right)/2\\ data\left( {n\_data - n + 1:n\_data,j} \right),i > n\_data - \left( {n - 1} \right)/2,\\ data\left( {i - \left( {n - 1} \right)/2:i + \left( {n - 1} \right)/2,j} \right),else \end{array} \right. $ | (4) |
(2) 计算每个采样点对应的采样区间的均值xi,j':
| $ {x_{i,j}}' = \frac{1}{n}\sum\limits_{i = 1}^n {{x_{i,j}}} . $ | (5) |
(3) 计算该采样点与相邻采样点的相关系数,c(i,j)为第j道数据、第i点的相关系数值:
| $c\left( {i,j} \right) = \frac{{\sum\limits_{i = 1}^n {\left( {{x_{i,j}} - {x_{i,j}}'} \right)\left( {{x_{i,j + 1}} - {x_{i,j + 1}}'} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {\left( {{x_{i,j}} - {x_{i,j}}'} \right)\left( {{x_{i,j + 1}} - {x_{i,j + 1}}'} \right)} } }}. $ | (6) |
(4) 遍历所有采样点及雷达数据道得到相关系数矩阵C。
(5) 在相关系数矩阵的每列中找到最后一个高相关的脉冲的位置,确定雷达极限探测深度。
2 仿真验证通过建立模拟仿真模型,验证两种计算探测深度方法的有效性。
具体的仿真流程如下:首先搭建电磁波传播的介质模型,设置接收天线的最小可检测幅值,当回波信号小于该幅值时,以高斯噪声为主。利用设定的最小可检测幅值,可以预先计算出雷达的极限探测深度作为真实值,然后再利用两种探测深度的计算方法从雷达数据的角度计算极限探测深度,并将计算结果与最小可检测幅值算出的真实值进行比对,验证基于相关系数法计算结果的有效性。
搭建的仿真模型如图 1,模型为多层介质,模型大小2 m × 5 m,其中最上方为空气,依次向下包含了8种介质,其相对介电常数也逐渐增加,分别为2.9、5、10、13、17、21、25、30;天线包含一个发射天线和两个接收天线(Rx_A,Rx_B),接收天线位于发射天线的两侧,收发天线间距均为10 cm,天线距离第1层介质40 cm。发射激励波形采用雷克子波,中心频率为400 MHz,时窗为240 ns,采样率为84.8 GHz。通过在x轴方向移动天线,获取在该模型下的雷达剖面数据。
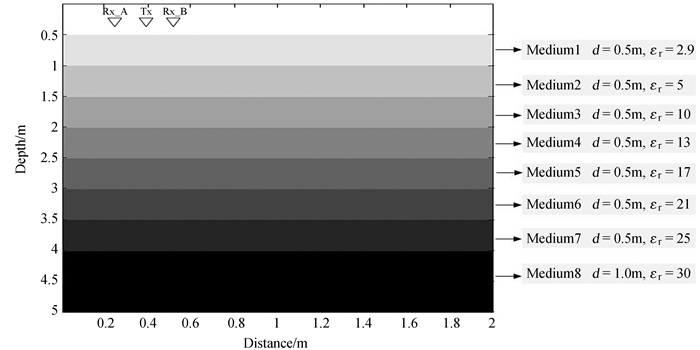
|
| 图 1 仿真模型示意图 Fig. 1 The configuration in the simulation |
理想的雷达单道波形如图 2。理想情况下,接收天线可以识别任意小的回波信号,在图 2中,每个反射层位的反射信号均被天线接收,各个反射信号在单道波形上能清晰分辨。
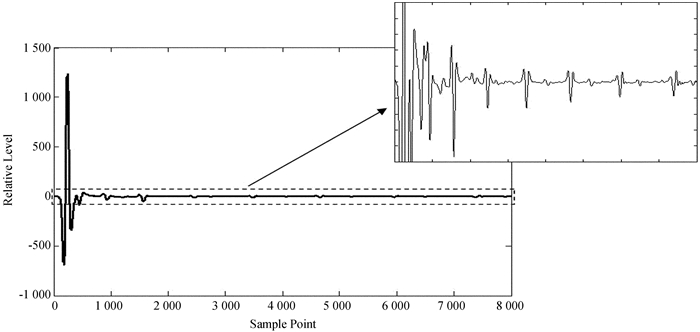
|
| 图 2 理想的单道波形及局部放大图 Fig. 2 ideal signal and the partial enlarged view |
为了更加接近实际情形(接收天线存在最小可检测功率/幅度,当回波信号强度小于该值时,信号无法被检测),设定A天线的最小可检测信号的相对强度为10,如果回波信号相对强度小于10,则该信号不能被检测出来,同时整个时窗内由均值为0、标准差为5的高斯白噪声填充;设定B天线的最小可检测信号的相对强度为14,如果回波信号相对强度小于14则该信号不能被检测出来,同时整个时窗内由均值为0、标准差为7的高斯白噪声填充。图 3给出了改进后A天线和B天线接收到的信号,为了较好地显示弱信号,相对幅值显示范围设定在-50到50的区间。
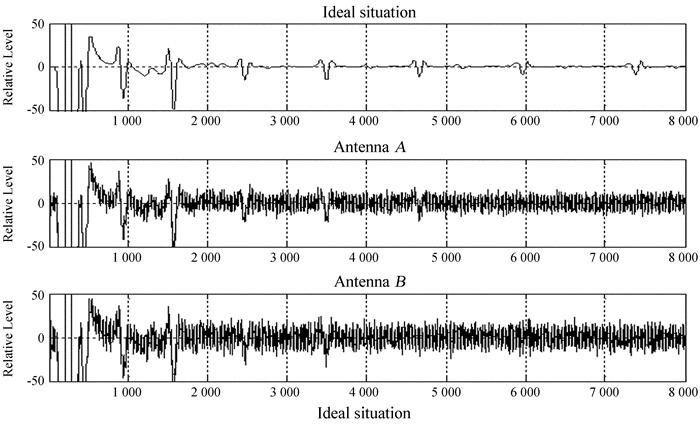
|
| 图 3 改进后的接收天线接收波形的对比图 Fig. 3 Waveform comparison after the receiving antenna is improved |
从图 3可以看出,由于A天线最小可检测相对幅度为10,由于第7和第8个回波信号幅度小于10,所以在A天线的单道接收波形中,只检测到了前6个回波信号,且第6个回波位于4 664点;B天线最小可以检测相对幅度为14,由于第6、第7和第8个回波信号幅度小于15,在B天线的单道接收波形中,只能检测到前5个回波信号,且第5个回波位于3 493点。A天线和B天线添加噪声之后,从图 3中得出A天线的极限探测深度为4 664点;B天线的极限探测深度为3 493点。接下来结合子波法和道相关法对雷达数据进行处理,计算两个天线的极限探测深度,验证两种方法能否准确地确定深度位置。
2.1 基于子波法的计算结果首先,子波的获取可以通过搭建自由空间模型得出。搭建的模型示意图及获取的子波如图 4和图 5。在图 4中,发射天线与接收天线的距离为10 cm,与先前仿真天线距离一致,天线置于自由空间,边界采用吸收边界。图 5显示了获取的子波波形,获取子波的宽度为347个采样点。
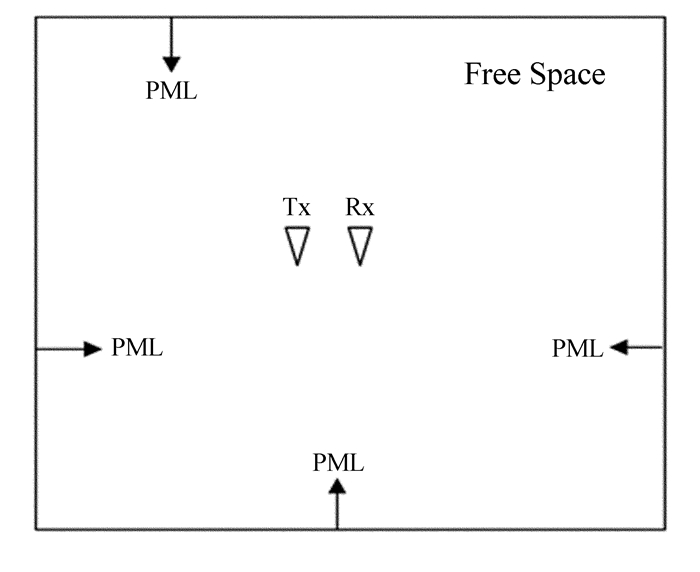
|
| 图 4 获取子波模型示意图 Fig. 4 The configuration in the simulation of acquiring wavelet |
|
| 图 5 子波波形 Fig. 5 The wavelet |
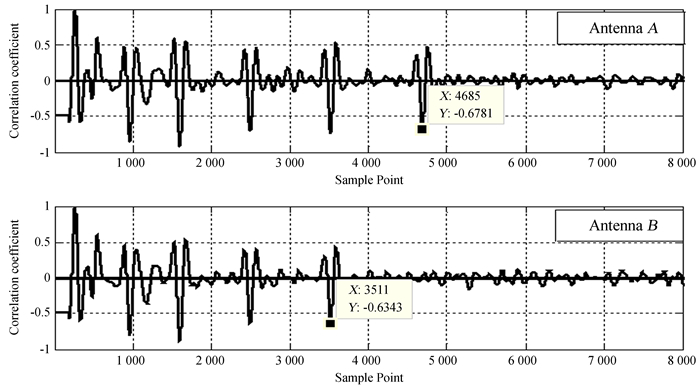
利用子波法得到相关系数波形如图 6,取最后一个相关信号的波谷作为探测深度位置,利用子波法得出A天线的极限探测深度为4 685,B天线的极限探测深度为3 511。同时,由图 6可以看出,雷达在与子波相关后,各个层位信息与原始回波信号相比,更加易于识别,所以利用子波法进行探测深度分析,还能起到提取精确反射层位置的作用。
|
| 图 6 基于子波法的计算结果 Fig. 6 The results based on the wavelet |
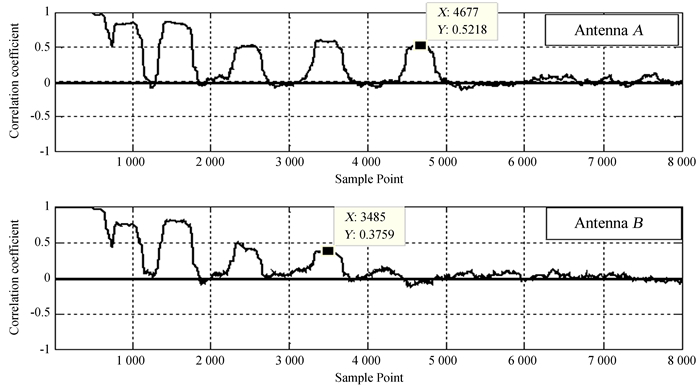
首先估计各采样点的处理区间大小,子波宽度在300点左右,程序设定的各个采样点的处理区间为351,大于一个子波的宽度。图 7为结合道相关法对探测深度估计的计算结果,取相关包络中间位置作为探测深度值,得出A天线的极限探测深度为4 677点,B天线的极限探测深度为3 485点。
|
| 图 7 基于道相关法的计算结果 Fig. 7 The results based on trace correlation method |
相关系数法,无论是道相关还是子波法都是通过相关性对有用信号进行放大,噪声信号进行压缩,在得到的相关系数曲线中确定最后一个有用信号的位置,对比图 3、图 6和图 7,有用信号较周边噪声信号幅度明显增强,相对于原始天线接收信号而言更容易确定最后一个有用信号的位置,这验证了相关系数法的有效性。至于如何确定最后一个高相关信号,对于分层清晰、回波信号结构完整的情形,可以直接从相关曲线中确定;对于结构复杂,回波信号混叠在一起的情形,可根据具体情况采用一阶偏导求极值,寻找第1个过0点以及采用统计法统计得出阈值等方法。
表 1给出了A天线和B天线两组数据的实际极限深度和利用两种方法计算得出的深度对比图。子波法在计算A天线的极限深度时偏差小于0.45%,B天线的极限深度偏差小于0.51%。道相关法在计算A天线的极限深度时偏差小于0.27%,B天线的极限深度偏差小于0.25%。结果表明,两种方法在结合雷达数据进行探测深度估计时,都能准确计算出雷达的极限探测深度,误差小于1%;道相关法略优于子波法,推测原因是因为子波法需要子波输入,子波无法做到完全一致估计,可能会带来一些误差。另外,两种方法计算的结果和真实值略有偏差,推断原因一方面可能是因为计算机仿真精度,仿真自带的不可消除的误差;另一方面可能是因为加入了较强的高斯白噪声,对计算结果产生一些影响。
| A天线数据 | B天线数据 | ||
| 极限深度 | 真实值 | 4 664 | 3 493 |
| 子波法计算值 | 4 685 | 3 511 | |
| 道相关法计算值 | 4 677 | 3 485 |
基于相关系数的计算方法能较好地推断雷达的极限探测深度。子波法由于在计算过程中需要子波的输入,在实际应用中,子波不方便获取或者不能准确获取时,对计算准确性的影响较大,同时需要指出,子波法只适合于地质结构较单一的情形,如果地下结构复杂,多次反射叠加会破坏波形,此时利用子波法往往不能得出一个较好的结果;道相关法仅依据实测的雷达数据,基于有用信息在相邻道之间的高相关性和噪声在相邻道之间的随机相关性的特点,能很准确地计算出探测深度,由于该方法不结合子波,不需要保证雷达回波信号的包络整体性,所以即使地下结构较复杂,也能取得较好的结果。
3 结 论针对传统雷达探测深度计算方法中存在先验性假设的不足,本文给出了两种基于相关系数法计算探测深度的方法。当子波已知或比较容易获取,同时地下分层结构较单一,可以采用子波法进行探测深度估计;当子波未知,地下结构较复杂时,可以尝试使用道相关法。文中通过仿真验证了两种方法的有效性,最后需要指出本文只是提出结合雷达数据进行探测深度估计的一种思路,虽然两种方法在仿真时能取得较好的结果,但在处理雷达数据时,考虑到信号波形、空间环境、设备状态等,需要在应用中加入更多的参考因素进行深入研究。
| [1] | 曾昭发, 刘四新, 冯晅, 等. 探地雷达原理与应用[M]. 北京: 电子工业出版社, 2010. |
| [2] | 丁春雨, 封剑青, 郑磊, 等. 雷达探测技术在探月中的应用[J]. 天文研究与技术, 2015, 12(2): 228-243. Ding Chunyu, Feng Jianqing, Zheng Lei, et al. A review of application of radar-detection techniques in lunar explorations[J]. Astronomical Research & Technology, 2015, 12(2): 228-243. |
| [3] | Fang Guangyou, Zhou Bin, Ji Yicai, et al. Lunar penetrating radar onboard the Chang'e-3 mission[J]. Research in Astronomy and Astrophysics, 2014, 14(12): 1607-1622. |
| [4] | Su Yan, Fang Guangyou, Feng Jianqing, et al. Data processing and initial results of Chang'e-3 lunar penetrating radar[J]. Research in Astronomy and Astrophysics, 2014, 14(12): 1623-1632. |
| [5] | Zhang Jinhai, Yang Wei, Hu Sen, et al. Volcanic history of the Imbrium basin: a close-up view from the lunar rover Yutu[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(17): 5342-5347. |
| [6] | 邢树果, 苏彦. 基于测月雷达机制月壤相对介电常数反演方法模拟研究[J]. 天文研究与技术, 2015, 12(3): 306-311. Xing Shuguo, Su Yan. Simulation and research of inversion method of the regolith relative permittivity based on principle of lunar penetrating radar[J]. Astronomical Research & Technology, 2015, 12(3): 306-311. |
| [7] | Davis J L, Annan A P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy[J]. Geophysical Prospecting, 1989, 37(5): 531-551. |
| [8] | 李雪萍, 纪弈才, 卢伟, 等. 车载探地雷达信号在分层介质中的散射特性[J]. 物理学报, 2014, 63(4): 1-8. Li Xueping, Ji Yicai, Lu Wei, et al. Characteristics of electromagnetic scattering from the vehicle-mounted ground penetrating radar in layered media[J]. Acta Physica Sinica, 2014, 63(4): 1-8. |
| [9] | 赵永辉, 吴建生, 万明浩, 等. 不同地下介质条件下探地雷达的探测深度问题分析[J]. 电波科学学报, 2003, 18(2): 220-224. Zhao Yonghui, Wu Jiansheng, Wan Minghao, et al. The analysis of detectable range of ground penetrating radar system in different underground medium[J]. Chinese Journal of Radio Science, 2003, 18(2): 220-224. |
| [10] | 雷林源. 探地雷达应用中的几个基本问题[J]. 物探与化探, 1988, 22(6): 408-414. Lei Linyuan. Some basic problems in the application of ground penetration radar[J]. Geoophysical & Geochemical Exploration, 1988, 22(6): 408-414. |
| [11] | Tugnait J K. Time delay estimation with unknown spatially correlated Gaussian noise[J]. IEEE Transactions on Signal Processing, 1993, 41(2): 549-558. |
| [12] | Coppens F. First arrival picking on common-offset trace collections for automatic estimation of static corrections[J]. Geophysical Prospecting, 1985, 33(8): 1212-1231. |
| [13] | 张先武. 探地雷达深度分辨率及其增强方法研究[D]. 北京: 中国科学院电子学研究所, 2013. |


