太阳光球表面布满了米粒状结构,在米粒的暗径中有一些发亮的结构,称为光球亮点(Photospheric bright points, PBPs)。普遍认为,光球亮点与磁场有密切关系,通过研究光球亮点可以促进太阳磁场的研究,促进更深层和更热的等离子体和日冕加热等太阳物理现象的研究[1]。但是,光球亮点很容易和发亮的碎米粒以及其他局部强度较高的太阳表面小尺度特征相混淆。目前在二维图像上识别亮点主要采用阈值法、区域生长法和形态学等几种技术。阈值法通过设置一个或几个阈值将图像的灰度级分为几部分,认为属于同一部分的像素是同一个物体[2-3];区域生长法是从初始区域开始,将相邻的具有同样性质的像素或其它区域归并到目前的区域中,从而逐步增长区域,直至没有可以归并的点或其它小区域为止[4];形态学是用具有一定形态的结构元素度量和提取图像中的对应形状以达到对图像分析和识别的目的。但这些方法在识别时一部分发亮的碎米粒会被误识别为亮点。
数据清洗是近年来随着数据挖掘的发展而出现的一门新兴技术,是指从数据集中发现并纠正“脏数据”,即从数据文件中检测出错误和不一致的数据,并剔除或修正它们,以提高数据质量[5-6]。
近年来国内外学者提出通过聚类方法实现数据清洗[7]。聚类分析是将研究对象分为相对同质的群组的统计分析技术,目的是发现数据间的关系,将相似的归为一类,相异的互为一类[8-9]。按照聚类分析算法的主要思路,聚类算法可以归纳为划分法、层次法、基于密度的方法、基于网格的方法和基于模型的方法[10]。其中,基于划分和基于密度是两种高效的适合大型数据集的聚类方法,常用于图像分析、图像处理等领域。
本文提出采用聚类分析的K-means算法和DBSCAN算法对亮点数据进行清洗,达到将非亮点结构从亮点结构中剔除的目的。论文第1节介绍了数据的来源以及数据的提取;第2节介绍了聚类数据的预处理和聚类方法;第3节介绍了光球亮点进行清洗后的结果和分析;第4节进行总结。
1 数据 1.1 数据来源本文的实验数据是Hinode/Solar Optical Telescope (SOT; Ichimoto et al. 2004; Suematsu et al. 2008)于2007年2月19日18时19分到20时40分在G波段观测的日面中心附近宁静区的高分辨序列图像。该组数据的像元分辨率为0.054 arcsec/pixel,视场大小为20 arcsec×20 arcsec,时间分辨率为11 s,一共由758张图组成。图 1(a)为序列中的第1帧高分辨图像。

|
| 图 1 (a)Hinode上的SOT于2007年12月19日在G-band观测的日面中心附近的高分辨像; (b)用LMD识别的亮点在原图中点亮的结果 Figure 1 (a) The G-band image observed with the SOT onboard the Hinode at 18:19 UT on 2007 February 19; (b) The PBPs detected by LMD algorithm |
首先用一个基于局部相关的亚像元级对齐算法把序列图像对齐[11],然后采用拉普拉斯形态学算法(Laplacian and Morphological Dilatation, LMD)识别光球亮点。图 1(b)显示了识别出的亮点在原图点亮的结果。
在序列图像的每一幅图上识别出亮点后,采用三维时空立方体的思想对光球亮点以26联通的思想跟踪[12]。如果一个亮点在生命期中没有发生过合并或者分裂,则称之为孤立点,否则称为非孤立点。在三维立方体中,孤立点的演化过程表现为一个圆柱形结构,其水平速度显示为这个圆柱状结构在时间轴上的扭曲情况,而生命周期就是这个圆柱状结构在时间轴上的开始和截止。
1.2.2 亮点数据特征提取经分析,亮点的等效直径、强度、偏心率、亮点边缘暗径比例、速度、运动方式和扩散系数等特征值作为分类的数据比较合理,因为这7个属性相关度较低,并且能代表亮点的光学强度、形态和运动等方面的特点。其定义如下:
等效直径:将每一个亮点对应的所有像素点作为面积,将其等效为圆计算等效直径。
最大强度比:用亮点的最大强度除以整幅图的平均强度描述亮点的强度。
偏心率:用椭圆两焦点间的距离除以长轴长度描述亮点的形状。偏心率越大,说明越偏向于长椭圆,反之则说明越偏向于圆形。
亮点边缘暗径比例:亮点的一个重要特性是其位于米粒暗径,因此提取了每一个亮点边缘位于暗径的比例。
速度:通过亮点的质心位置获取每两帧之间的位移计算亮点的速度。
运动方式:定义一个mt,其值为位移除以运动轨迹长度和。位移公式如(1)式;1为起始帧,n为结束帧,表示亮点的首尾位移;运动轨迹长度和定义为(2)式,(3)式即为生命期内所有位移之和。根据定义,mt可以用来定量描述亮点的运动轨迹,其值范围为0到1。如果mt=1,则意味着亮点的运动轨迹为直线;如果mt=0,则表示亮点从起始点出发又回到原点。因此mt越接近1则亮点沿着接近直线的轨迹运动,越接近0,则亮点的轨迹近似于圆形。
扩散系数:扩散系数是描述亮点的扩散面积与时间的关系,定义为(4)式,其中〈(Δt)2〉代表亮点在生命期中任意时刻的位置与初始位置的平方位移;γ是扩散系数;Т是亮点的生命期。扩散系数越大,在单位时间内扩散的面积越大,反之亦然。
| $\text{Displacement=}\sqrt{{{\left[ X\left( n \right)-X\left( 1 \right) \right]}^{2}}+{{\left[ Y\left( n \right)-Y\left( 1 \right) \right]}^{2}}}$ | (1) |
| $\text{Totallength=}\sum\limits_{t=1}^{n}{\sqrt{\Delta X{{\left( t \right)}^{2}}+\Delta Y{{\left( t \right)}^{2}}}}$ | (2) |
| $\Delta X\left( t \right)=X\left( t+1 \right)-X\left( t \right),\Delta Y\left( t \right)=Y\left( t+1 \right)-Y\left( t \right)$ | (3) |
| $\left\langle {{\left( \Delta T \right)}^{2}} \right\rangle =C{{T}^{\gamma }}.$ | (4) |
这7个属性中,由于每个亮点在生命期内等效直径、强度、偏心率、亮点边缘暗径比例和速度这5项有多个属性值,因此先分别计算每个亮点在生命期内这5个属性的平均值分别代表其一生的一个平均状态,比如平均直径、平均强度、平均偏心率、平均边缘暗径比例和平均速度。
2 聚类 2.1 数据预处理 2.1.1 数据标准化由于这7个属性的量纲不同,因此需要先对数据进行标准化处理。标准化指去除数据的单位限制,将其转化为无量纲的纯数值,以便于不同单位或量级的指标能够进行比较和加权。采用z-score标准化方法。基本思想是基于原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化,定义为:
| ${{x}^{*}}=\frac{x-\mu }{\sigma },$ | (5) |
其中,μ为所有样本数据的均值;σ为所有样本数据的标准差。标准化后的数据符合标准正态分布,即均值为0,标准差为1。
2.1.2 数据降维高维数据包含了大量冗余的信息,因此采用特征降维的方法对这7列数据进行降维处理。特征降维是指在所有的特征数据中选择几个基本能代表所有特征数据包含的信息的主要特征数据,一般有两类方法:特征选择和特征抽取。特征选择即从高纬度的特征中选择其中的一个子集作为新的特征;而特征抽取是指将高纬度的特征经过某个函数映射至低纬度作为新的特征。
主成分分析(Principal Components Analysis, PCA)是一种无监督特征抽取降维方法,利用特征数据的内在关联结构,通过线性变换将多维的特征数据变换为维度较少包含原有特征大部分信息且相互独立的特征数据。由于各项特征数据不存在人为关联,可使得最后清洗亮点的结果更为合理,因此采用主成分分析对亮点的七维特征数据进行降维。主成分分析的降维过程描述如下:
首先用每个样本的多个特征数据构造一个特征数据矩阵,如(6)式。其中,n代表第几维特征数据;p代表某维的第几个特征数据。
| $X=\left[ \begin{matrix} {{X}_{11}} & {{X}_{12}} & \cdots & {{X}_{1p}} \\ {{X}_{21}} & {{X}_{22}} & \cdots & {{X}_{2p}} \\ \vdots & \vdots & {} & \vdots \\ {{X}_{n1}} & {{X}_{n2}} & \cdots & {{X}_{np}} \\ \end{matrix} \right]$ | (6) |
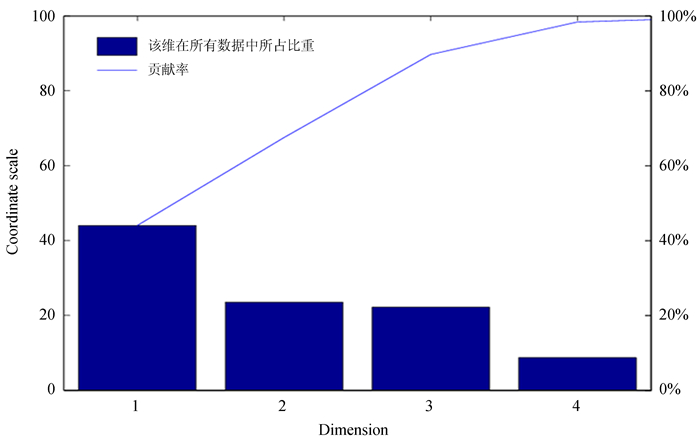
然后计算原始数据的协方差矩阵,得到每维数据间的关系;通过协方差矩阵算出特征向量和特征值,将特征值由大到小排列,给出成分的重要性级别选择降维目标数k,最后用协方差矩阵的前k列乘以原始数据矩阵,即得到降维后的数据矩阵。其中,k的选择通过分析贡献率确定,贡献率表示所定义的主成分在整个数据分析中承担的主要意义占多大的比重,当取前k个主成分代替原来全部变量时,累计贡献率的大小反应了这种取代的可靠性,累计贡献率越大,可靠性越大;反之,则可靠性越小。亮点的7列标准化后的数据通过主成分分析降维后,主成份的贡献率如图 2,降至一维的贡献率仅为46%,二维的为71%,到第三维时贡献率已达到90%,这意味着三维数据已能代表原始数据90%的意义,因此将七维数据选择降至三维。
|
| 图 2 贡献率与主成分的关系 Figure 2 Relation between the rate of contribution and principal component |
K-means也称为K-均值,是划分聚类方法中最具代表性的一种算法[13]。该算法通过最近距离的原则把n个对象划分为k个簇,以使簇内具有较高的相似度。算法首先随机选择k个对象,每个对象初始代表了一个簇的平均值或中心。然后对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇,再重新计算每个簇的平均值[14-15]。该过程不断迭代,直到准则函数收敛。准则函数定义为
| $E=\sum\limits_{i=1}^{k}{{{\sum\limits_{x\in {{c}_{i}}}{\left\| x-{{{\bar{x}}}_{i}} \right\|}}^{2}},}$ | (7) |
其中,x是空间中的点,表示给定的数据对象,是簇的平均值,该准则的主要目标是使生成的簇尽可能地紧凑和独立。
2.2.2 DBSCAN算法聚类DBSCAN是一种基于密度的聚类算法。该算法把具有足够高密度的区域划分为簇,并可以发现任意形状的聚类,它定义簇为基于密度的点的最大集合。描述该算法之前需做以下定义:
定义1(ε-邻域):给定对象半径ε内的区域称为该对象的ε-领域。
定义2(核心对象):如果一个对象的ε-领域至少包含最小数目MinPts个对象,则称该对象为核心对象。
定义3(直接密度可达):给定一个对象集合D,如果p在q的ε-邻域内,而q是一个核心对象,则对象p从对象q出发是直接密度可达的。
定义4(密度可达):如果有一个数据对象序列p1,p2,…,pn∈D,其中p1=q, pn=p,并且pi+1是从pi直接密度可达的,则称p是从q关于ε和MinPts密度可达的。
定义5(密度相连):如果存在一个数据对象O使得p和q都是从O关于ε和MinPts密度可达的,则称p和q是关于ε和MinPts密度相连的。
DBSCAN算法的流程可描述如下[16]:首先通过检查数据库中每个点的ε-邻域寻找聚类。如果一个点p的ε-邻域内含多于MinPts个点,则建一个以p作为核心对象的新簇。然后,DBSCAN反复地寻找从这些核心对象直接密度可达的对象,这个过程可能涉及一些密度可达簇的合并。当没有新的点可以被添加到任何簇时,该过程结束。
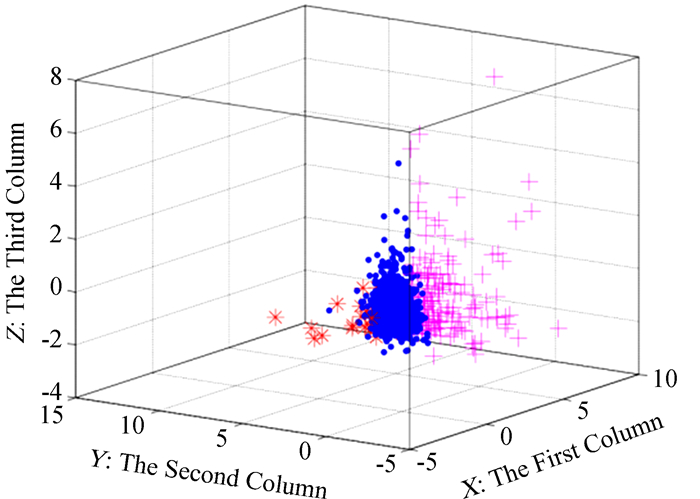
3 结果 3.1 K-means算法聚类结果K-means算法在设置清洗目标数为2时的结果如图 3,图中,实心圆型(蓝色)代表亮点,十字型(玫红色)和米字型(大红色)代表噪声点。但对照原始图像发现噪声点的数目过多,把很多亮点也包含在内,因此对第1次清洗出的噪声点再用K-means进行第2次清洗,结果如图 3中的十字型(玫红色)和米字型(大红色)点,米字型(大红色)即为第2次清洗出的噪声点。
|
| 图 3 K-means算法清洗数据的结果 Figure 3 The cleaning result of the K-means algorithm |
为检验清洗的结果是否有效,首先将第2次
清洗后的结果通过不同颜色显示在二维图中。图 4显示的是其中一帧二维图像,(a)是原图,(b)中蓝色代表亮点,红色代表噪声点。由于采用特征数据表示亮点的演化特征,因此在三维时空立方体中通过不同的颜色标注噪声点和亮点的三维演化结构,如图 4(c),红色代表噪声点,蓝色代表亮点。从亮点的三维演化结构可以看到,噪声点的三维演化结构有长有短,有大有小,运动的轨迹也是各式各样,因此进一步在时间序列图中分析K-means算法清洗的结果。

|
| 图 4 (a)原图;(b)K-means算法清洗的亮点在二维图上的显示; (c)K-means算法清洗结果在三维时空立方体中的显示 Figure 4 (a) One G-band image; (b) The cleaning result of the K-means algorithm of (a); (c) The cleaning result of the K-means algorithm in the three-dimension space-time cube |
图 5显示了亮点和噪声点在其生命期中的演化情况。用不同的颜色标记用K-means算法清洗后的亮点以及噪声点的演化过程,红色代表噪声点,蓝色代表亮点。对照图(a)和(b),圈1、2和3对应的位置上分别示意了3种不同的演化情况:圈1对应的位置是一个自始至终在米粒暗径中的亮点;圈2对应的位置是一个自始至终在米粒上的噪声点;而圈3则反应了另一种情况,K-means算法分类是一个亮点,但在对应位置上看到其在19:02:50 UT时在米粒上,所以清洗存在误差。K-means算法一共清洗出29个噪声点,通过分析所有的演化发现满足非亮点结构的有23个,即K-means算法清洗的正确率为80%。

|
| 图 5 (a)一段序列图;(b)K-means算法清洗的亮点演化 Figure 5 (a) A time-series; (b) Evolution of corresponding PBPs cleaned by the K-means algorithm |
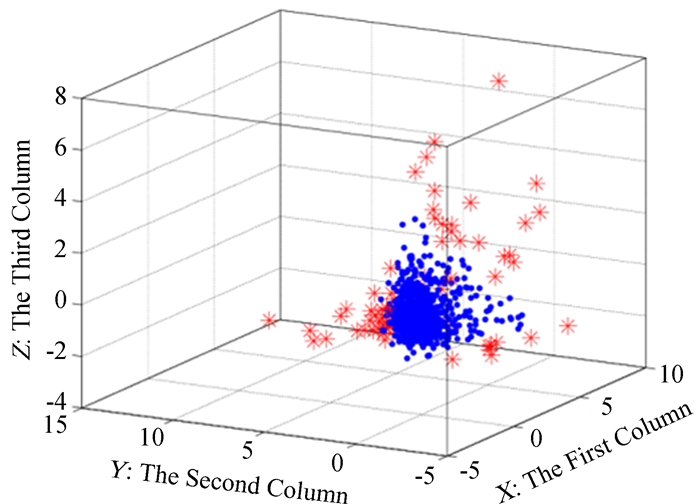
DBSCAN算法清洗结果如图 6,图中,实心圆型(蓝色)代表亮点,米字型(红色)代表噪声点。
|
| 图 6 DBSCAN算法清洗结果 Figure 6 The cleaning result of the DBSCAN algorithm |
为检验清洗的结果是否有效,将清洗后的结果通过不同颜色显示在二维图中。图 7显示了其中一帧二维图像,(a)是原图,(b)中蓝色代表亮点,红色代表噪声点。

|
| 图 7 (a)原图;(b)DBSCAN算法清洗的亮点在二维图上的显示;(c)DBSCAN算法清洗结果在三维时空立方体中的显示 Figure 7 (a) One G-band image; (b) The cleaning result of the DBSCAN algorithm corresponding (a); (c) The cleaning result of DBSCAN algorithm in the three-dimension space-time cube |
在三维时空立方体中通过不同的颜色标注噪声点和亮点的三维演化结构如图 7(c),红色代表噪声点,蓝色代表亮点。
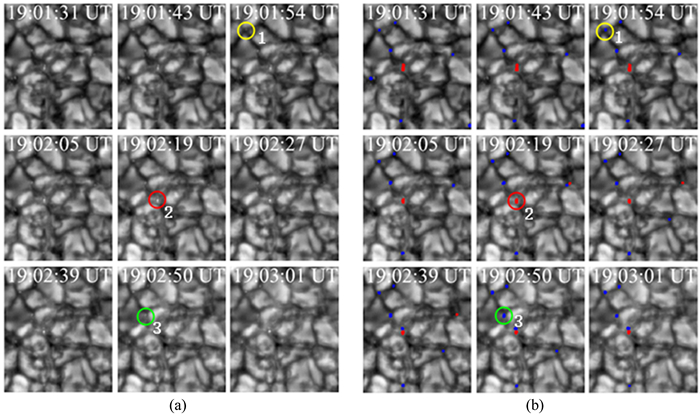
进一步在时间序列图中分析DBSCAN算法清洗的结果。图 8显示了亮点和噪声点在其生命期中的演化情况。用不同的颜色标记了用DBSCAN算法清洗后的亮点以及噪声点的演化过程,红色代表噪声点,蓝色代表亮点。圈1、2和3对应的位置上分别示意了3种不同的演化情况:圈1对应的位置是一个自始至终在米粒暗径中的亮点;圈2对应的位置是一个自始至终在米粒上的噪声点;而圈3则反应了另一种情况,DBSCAN算法认为它是一个亮点,但在对应位置上看到其在19:02:50 UT时在米粒上,因此清洗存在误差。DBSCAN算法清洗出的噪声点数为38,通过分析亮点的演化得出:满足非亮点结构的有20个,即DBSACN算法清洗的正确率为53%。
|
| 图 8 (a)一段序列图;(b)DBSCAN算法清洗的亮点的演化 Figure 8 (a) A time-series; (b) Evolution of corresponding PBPs cleaned by the DBSCAN algorithm |
本文采用聚类方法清理亮点数据,以达到将非亮点结构从亮点结构中剔除的目的。首先采用LMD算法识别每一帧图像中的亮点,采用三维时空立方体思想进行跟踪。然后提取能代表亮点的光学强度、形状和运动特性的7个相关度较低的特征值,包括等效直径、强度、偏心率、亮点边缘在暗径中的比例、速度、运动方式和扩散系数。由于这些数据量纲不一致,首先采用zscore法进行标准化;又考虑到高维数据包含冗余和相关的信息,因此采用主成份分析法进行降维分析,选择90%的贡献率将数据降到三维。最后分别采用K-means算法和DBSCAN算法对光球亮点数据进行清洗。经过检验发现两种聚类算法均能达到将非亮点结构清洗出来的目的,但还存在一定的误差。K-means算法的正确率为80%,DBSCAN算法的正确率为53%。因此,K-means算法比DBSCAN算法更适合清洗非亮点结构。
本文提供了一个较好的方法剔除识别中不可避免的噪声,为小尺度的磁场研究清洗出更为准确的亮点数据,这对进一步研究日冕加热等问题提供了更为准确的数据。但是,从目前的结果可以看出,仍旧存在一些需要改进的地方。如算法的结果误差较大、对阈值和参数的选取有较大的依赖性;两个算法的不同,清洗的正确率有可能是因为其物理模型调整、清洗所需的参数及其权重导致的;亮点的等效直径、强度、偏心率等参数与空间分辨率有关系,因此对于不同分辨率的观测结果可能有不同的清洗结果。在今后的工作中,将进一步对算法进行改进,并考虑物理参数等因素,得到更为精确、合理的清洗结果。
致谢:
感谢Hinode团队提供数据。
| [1] | 刘艳霄, 杨云飞, 林隽. 太阳光球磁亮点的识别算法[J]. 天文研究与技术——国家天文台台刊 , 2014 , 11 (2) : 145 –150 Liu Yanxiao, Yang Yunfei, Lin Jun. A region-growth algorithm to recognize magnetic bright spots in the solar photosphere[J]. Astronomical Research & Technology—— Publications of National Astronomical Observatories of China , 2014 , 11 (2) : 145 –150. |
| [2] | Almeida J S, Bonet J A, Viticchié B, et al. Magnetic bright points in the quiet Sun[J]. The Astrophysical Journal Letters , 2010 , 715 (1) : L26 –L29. DOI: 10.1088/2041-8205/715/1/L26 |
| [3] | Bovelet B, Wiehr E. Multiple-scale pattern recognition applied to faint intergranular G-band structures[J]. Solar Physics , 2007 , 243 (2) : 121 –129. DOI: 10.1007/s11207-007-9010-x |
| [4] | Crockett P J, Jess D B, Mathioudakis M, et al. Automated detection and tracking of solar magnetic bright points[J]. Monthly Notices of the Royal Astronomical Society , 2009 , 397 (4) : 1852 –1861. DOI: 10.1111/mnr.2009.397.issue-4 |
| [5] | 王咏梅, 陈家琪, 耿玉良. 一种可交互的数据清洗系统[J]. 计算机工程与设计 , 2005 , 26 (4) : 955 –957 Wang Yongmei, Chen Jiaqi, Geng Yuliang. Interactive data cleaning system[J]. Computer Engineering and Design , 2005 , 26 (4) : 955 –957. |
| [6] | 郭志懋, 周傲英. 数据质量和数据清洗研究综述[J]. 软件学报 , 2002 , 13 (11) : 2076 –2082 Guo Zhimao, Zhou Aoying. Research on data quality and data cleaning:a survey[J]. Journal of Software , 2002 , 13 (11) : 2076 –2082. |
| [7] | 张燕.基于聚类算法的数据清洗的研究与实现[D].保定:华北电力大学, 2008. http://cdmd.cnki.com.cn/article/cdmd-10079-2008073934.htm |
| [8] | 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报 , 2008 , 19 (1) : 48 –61 Sun Jigui, Liu Jie, Zhao Lianyu. Study on clustering algorithms[J]. Journal of Software , 2008 , 19 (1) : 48 –61. DOI: 10.3724/SP.J.1001.2008.00048 |
| [9] | Xu R, Wunsch D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks , 2005 , 16 (3) : 645 –678. DOI: 10.1109/TNN.2005.845141 |
| [10] | Feng Song, Deng Linhua, Yang Yunfei, et al. Statistical study of photospheric bright points in an active region and quiet Sun[J]. Astrophysics and Space Science , 2013 , 348 (1) : 17 –24. DOI: 10.1007/s10509-013-1555-6 |
| [11] | 陈洁, 冯松, 邓辉, 等. 太阳磁场观测中相关位移叠加算法的比较[J]. 天文研究与技术——国家天文台台刊 , 2013 , 10 (2) : 201 –206 Chen Jie, Feng Song, Deng Hui, et al. Comparison of correlation-based techniques for correcting and stacking solar magnetic-field images[J]. Astronomical Research & Technology—— Publications of National Astronomical Observatories of China , 2013 , 10 (2) : 201 –206. |
| [12] | Yang Yunfei, Qu Huixue, Ji Kaifan, et al. Characterizing motion types of G-band bright points in the quiet Sun[J]. Research in Astronomy & Astrophysics , 2015 , 15 (4) : 569 –582. |
| [13] | Yu S, Tranchevent L C, Moor B D, et al. Optimized data fusion for kernel k-means clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2012 , 345 : 89 –107. |
| [14] | Ghosh S, Dubey S K. Comparative analysis of k-means and fuzzy c-means algorithms[J]. International Journal of Advanced Computer Science and Applications (IJACSA) , 2013 , 4 (4) : 35 –39. |
| [15] | Patel B C, Sinha D G R. An adaptive k-means clustering algorithm for breast image segmentation[J]. International Journal of Computer Applications , 2010 , 10 (4) : 35 –38. DOI: 10.5120/ijca |
| [16] | Zhou Aoying, Zhou Shuigeng, Cao Jing, et al. Approaches for scaling DBSCAN algorithm to large spatial databases[J]. Journal of Computer Science and Technology , 2000 , 15 (6) : 509 –526. DOI: 10.1007/BF02948834 |



