2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1m太阳望远镜(New Vacuum Solar Telescope,NVST)于2010年正式投入常规观测[1]。随着高分辨率成像观测系统、多波段光谱仪[2]、大色散光谱仪、磁分析仪等终端仪器逐步完善,望远镜的使用效率变得越来越重要,因此,需要充分利用有限的可观测晴天数。然而,1m太阳望远镜为了提高观测的圆顶视宁度,在观测过程中将圆顶平移使圆顶远离望远镜[3],在观测时,这种敞开式观测模式使得随机风载直接作用在望远镜上,最终导致焦面图像的抖动。目前,1m太阳望远镜通过提高伺服系统的钢度减小随机风载引起的图像抖动取得了一定的成效,使高分辨成像能工作在四级风左右[4, 5]。但1m太阳望远镜的光谱仪等终端仪器需要焦面图像有更小的抖动,依靠目前的伺服跟踪系统无法达到要求。
为进一步减少1m太阳望远镜焦面图像的抖动,使其能工作在更高的风速下,拟采用二维压电摆镜稳定风载引起的图像抖动。摆镜是近年发展起来的精密控制仪器,它不仅可以实现光束精确扫描镇定、光路调制以及光机抖动补偿[6],也可以实现目标指向、稳定空间以及精确的跟踪捕获。目前,它已被广泛用于空间光学望远镜、空间激光通信平台、天文望远镜、高分辨率侦查照相卫星、图像稳定、自适应光学等许多领域[7, 8, 9, 10, 11, 12, 13]。摆镜在天文上的应用主要是跟踪系统,也称为Tip-tilt低阶改正系统,是针对湍流大气引起的低阶图像抖动。但它与随机风载引起的图像抖动相比,频率更高,幅度更小。因此,摆镜在不同应用系统中的侧重点不同。
本文针对1m太阳望远镜随机风载下焦面图像抖动的特点,基于芯明天公司的XS-340.4SL二维压电摆镜和1m太阳望远镜氧化钛通道(以下简称TiO通道)的高分辨率成像观测系统,设计了摆镜图像稳定控制系统,并根据摆镜的实测性能和随机风载下焦面图像的实测误差,通过数值模拟的方法深入分析了系统的控制性能。文章第1节给出了摆镜图像稳定控制系统的光机结构设计;第2节通过实测分析了随机风载下1m太阳望远镜焦面图像抖动特性和摆镜系统特性;第3节通过数值模拟分析了摆镜图像稳定控制系统的具体性能;第4节根据摆镜的系统结构和数值模拟分析,在1m太阳望远镜的TiO通道对星展开跟踪实验,并给出实验结果;第5节对本文进行总结。
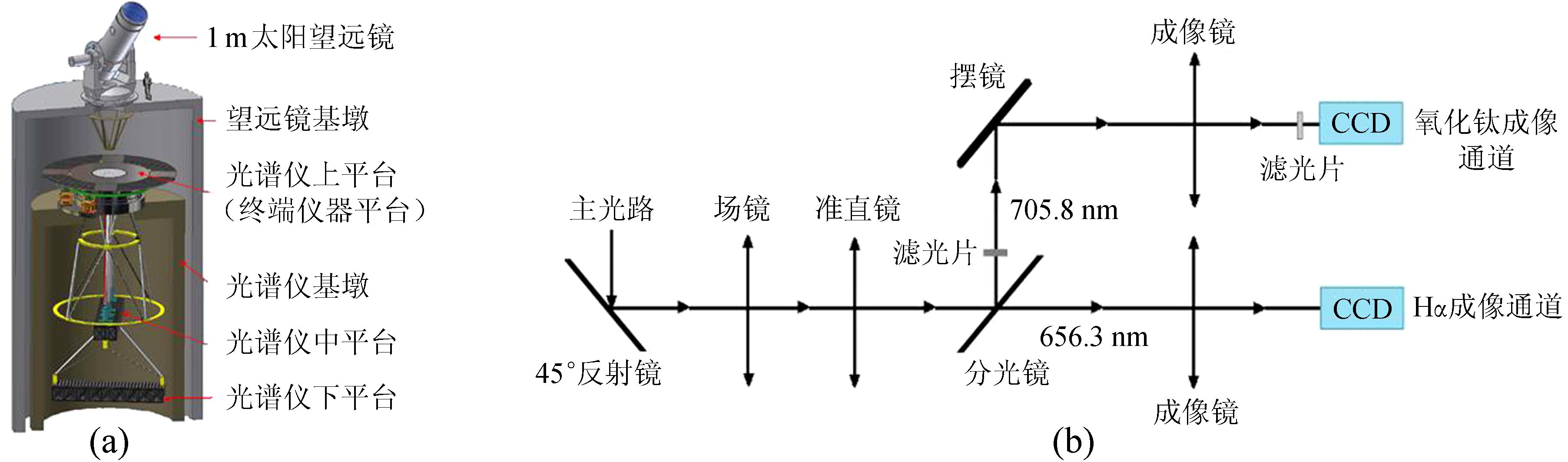
1 摆镜图像稳定控制系统的结构设计1m太阳望远镜剖面结构如图 1(a),终端仪器安放在光谱仪的上平台,观测时,整个平台与焦面像同步旋转。1m太阳望远镜高分辨率成像系统目前有两个通道,分别是705.8nm波段的TiO成像观测通道和656.3nm波段的Hα成像观测通道[14],二维摆镜安放在TiO通道中,如图 1(b)。由于是实验系统,经过摆镜出射的光路没有进行分光,因此,摆镜实验时,需要停止TiO通道的观测。
|
| 图 1 (a) 1m太阳望远镜剖面结构示意图;(b) 摆镜图像稳定系统安装结构 Fig. 1 (a) The sketch map of the cross section structure for the NVST; (b) The mounting structure of the tip-tilt mirror image stabilization system |
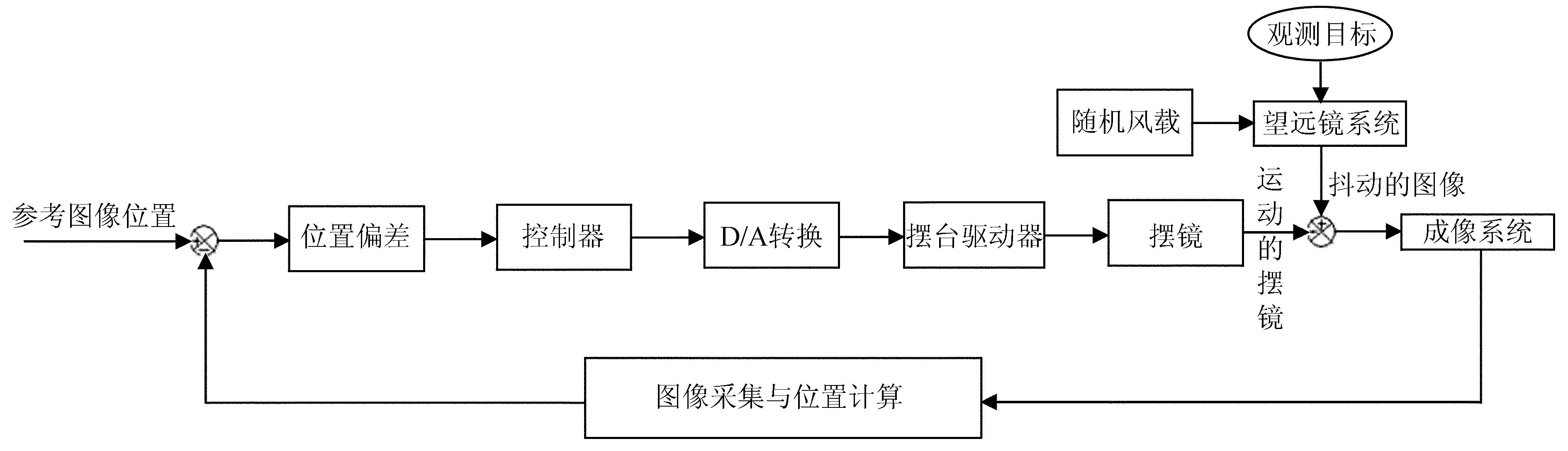
在图 1(b)的系统中,摆镜是芯明天公司型号为XS_340.4SL的二维压电偏摆台,摆台上的反射镜片直径30mm,厚6mm,摆台控制器为该公司的XE-501D控制器。根据图 1(b)的系统设计,摆镜的反馈控制信号通过TiO成像通道的CCD获得。闭环工作过程这样设计:闭环开始时刻,确定此时图像在CCD上的参考位置,当随机风载引起图像抖动时,会相对于参考位置随机抖动,通过获取TiO通道的图像可以计算出图像相对于参考位置的偏移量,然后将偏移量转化为摆镜控制器的电信号转动摆镜,使图像回到参考位置。摆镜图像稳定闭环控制系统的控制原理如图 2。
|
| 图 2 摆镜图像稳定闭环控制系统的控制原理图 Fig. 2 The control schematic of the closed-loop control system for the tip-tilt mirror image stabilization |
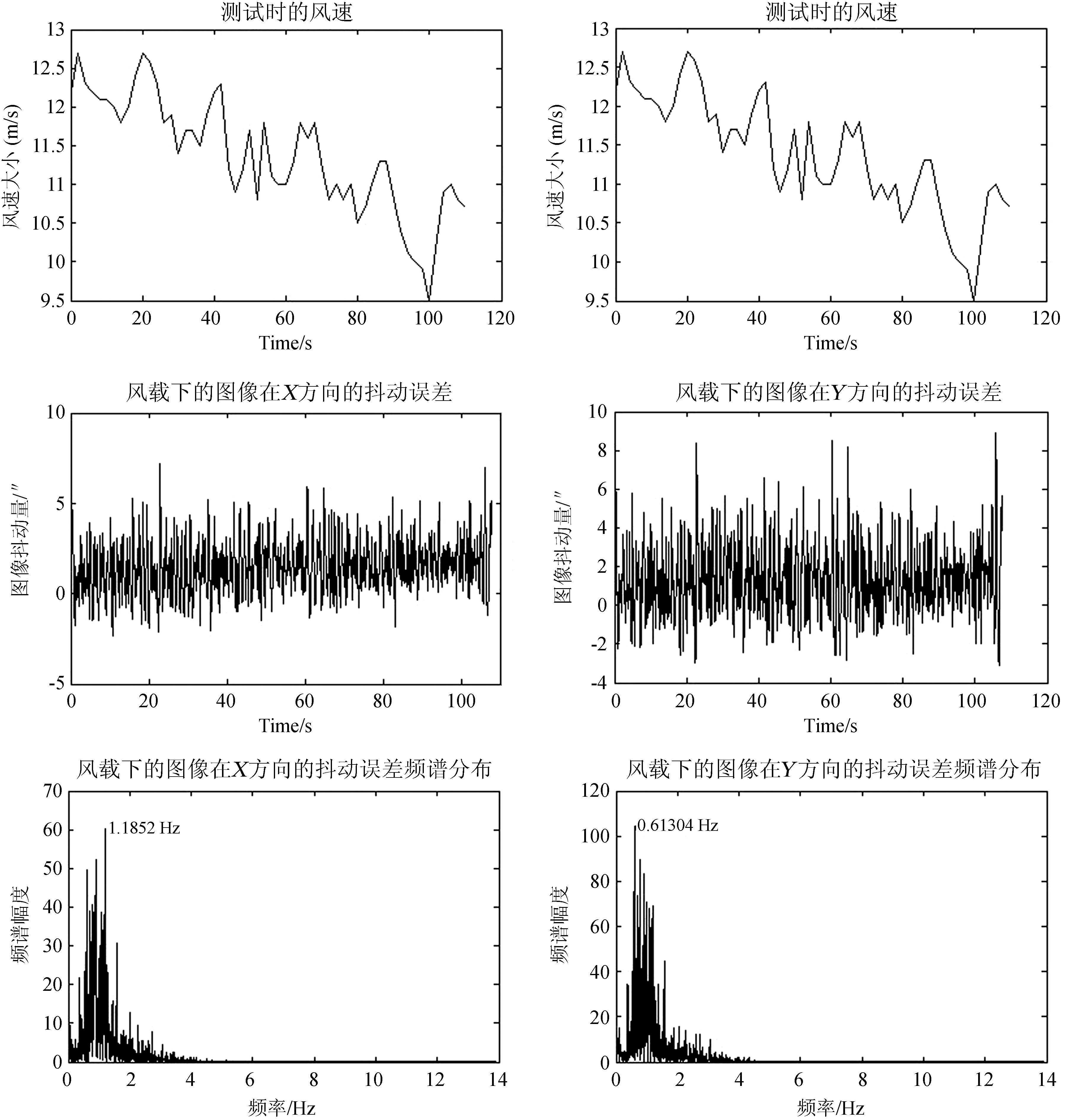
当随机风载作用在1m太阳望远镜的镜筒上时,能通过伺服系统误差以及光电导行全日面图像监测系统和高分辨率成像观测系统的图像抖动反应出来。在摆镜图像稳定系统中,主要关心的是高分辨率成像观测系统中TiO通道的图像抖动。实测时,望远镜的跟踪目标可以选择星,也可以是太阳上某个活动区。观测目标是星时,位置偏移量计算采用重心算法,观测目标是太阳上某个活动区时,则采用相关算法。本文的观测目标选择星,通过TiO高分辨率成像观测通道实测得到CCD靶面上X和Y两个正交方向的图像抖动以及频谱如图 3,相应的均方根值和峰峰值如表 1。根据图 3或表 1可以知道:六级风下,1m太阳望远镜焦面图像的抖动范围在12″左右,由此确定摆镜的最大偏转角应该大于此值;随机风载引起的图像抖动在1Hz左右,频率成分在5Hz以内。因此,大致可以估计摆镜图像稳定系统在控制随机风载引起图像抖动时所需的带宽不是很高。
|
| 图 3 随机风载作用下TiO通道的图像抖动及频谱分布 Fig. 3 The image jitter and its spectrum distribution of the TiO channel with the random wind load |
| X方向误差 | Y方向误差 | ||
| 均方根/″ | 峰峰值/″ | 均方根/″ | 峰峰值/″ |
| 1.3672 | 9.5030 | 1.7155 | 11.9859 |
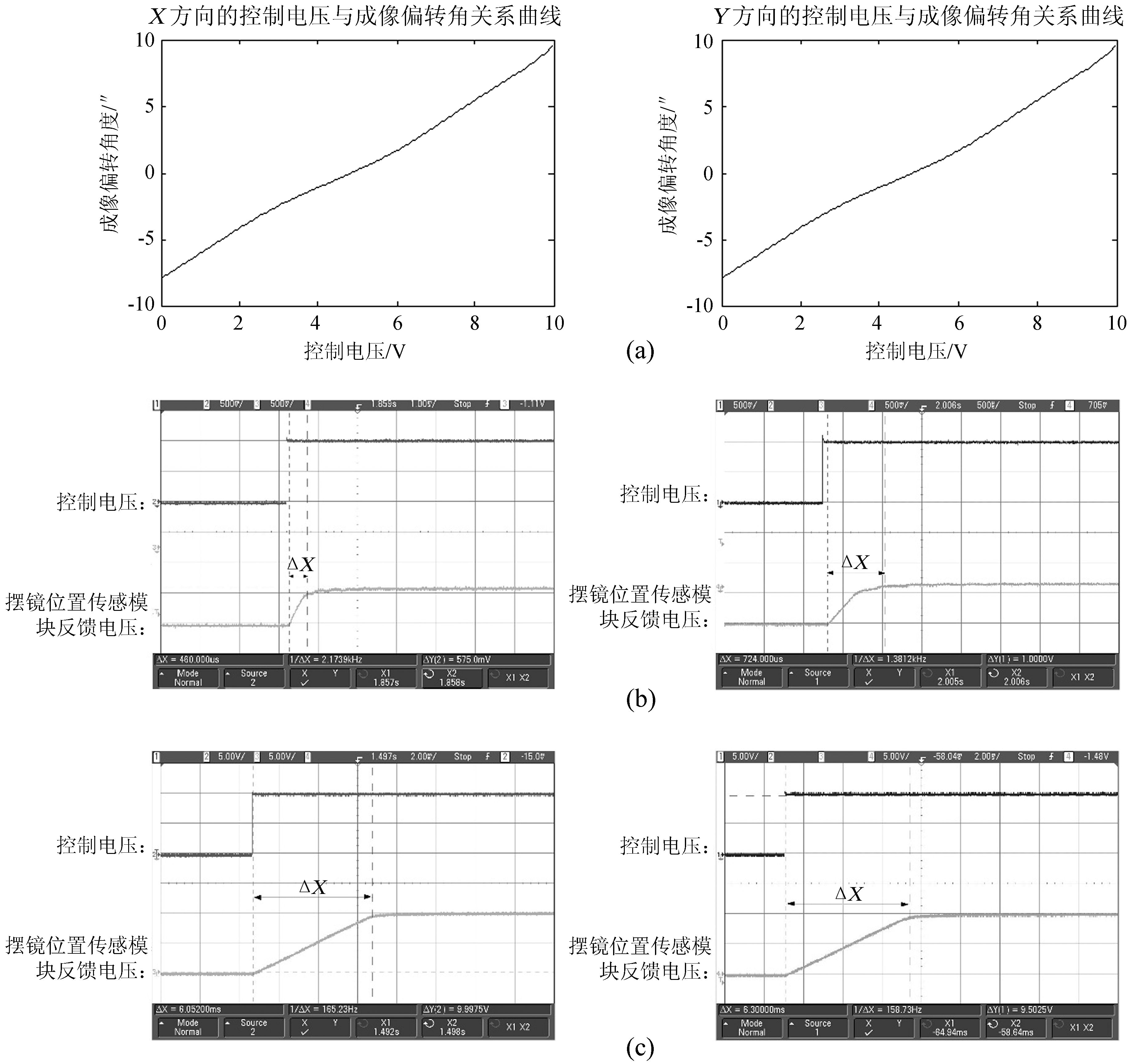
摆镜系统特性包括摆镜的静态特性和动态特性。摆镜的静态特性主要是摆镜的最大偏转角和响应曲线(电压-偏转角曲线),摆镜的动态特性主要是摆镜的阶跃响应和频率响应。静态特性测试时,在TiO成像观测通道的光路中加激光进行测试,摆镜控制器XE-501D输入端加入相应的控制电压,输入控制器的电压范围是0到10V,然后测试激光光斑重心随输入电压的变化。动态特性测试时,由于CCD需要一定的曝光时间和读出时间,无法达到动态特性测试所需的响应速度,因此,动态特性主要通过XE-501D控制器内部的压敏电阻位置传感器的反馈信号进行。XE-501D控制器可以工作在开环模式和闭环模式,XE-501D控制器的闭环工作模式主要校正摆镜系统的非线性度,但降低了系统响应速度。由于图像稳定闭环控制系统本身工作在XE-501D控制器更外层闭环控制回路,一定程度上可以改正摆镜系统的非线性带来的影响,而更需要摆镜系统有更快的响应速度。因此,图像稳定闭环控制系统工作时,将XE-501D控制器设置在开环模式,相应地,本文主要给出XE-501D控制器工作在开环模式时摆镜系统两个正交方向的动静态特性。图 4(a)为摆镜在控制器开环模式下在两个正交方向(分别与TiO通道的图像X方向和Y方向对应)的响应曲线。
|
| 图 4 (a) X、Y方向在摆镜控制器开环下的成像偏转角与控制电压关系曲线;(b) 控制电压在1V下 X、Y两个正交方向的阶跃响应曲线;(c) 控制电压在10V下X、Y两个正交方向的阶跃响应曲线 Fig. 4 (a) The relation curve of the control voltage and the imaging deflection angle in X and Y directions for the tip-tilt mirror controller working at the open-loop mode; (b) The step response curve in the orthogonal direction when the control voltage is 1V; (c) The step response curve in orthogonal direction when control voltage is 10V |
从图 4(a)可以看出,当控制器开环时,两正交方向上的响应曲线有一定的非线性关系,且非线性主要在参考0点附近。图 4(a)的数据是通过将摆镜加5V电压置中后得到的。当控制电压从0到10V变化时,摆镜可以正负方向转动。通过多项式拟合的方式,得到摆镜的电压-偏转角关系,表示为
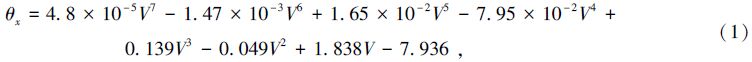
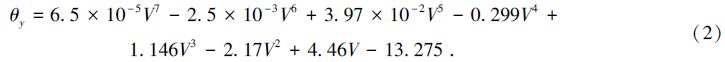
通过实验可知,系统的延迟时间与控制电压幅度无关,且在60μs左右。从图 4(b)和4(c)可以看出:当控制器的输入电压为1V时,X方向的阶跃响应时间460μs,Y方向的阶跃响应时间460μs,因此当控制电压在1V时,最高频率响应可达1KHz;输入电压为10V时,X方向的阶跃响应时间6.052ms,Y方向的阶跃响应时间6.3ms,因此最高频率响应在80Hz。
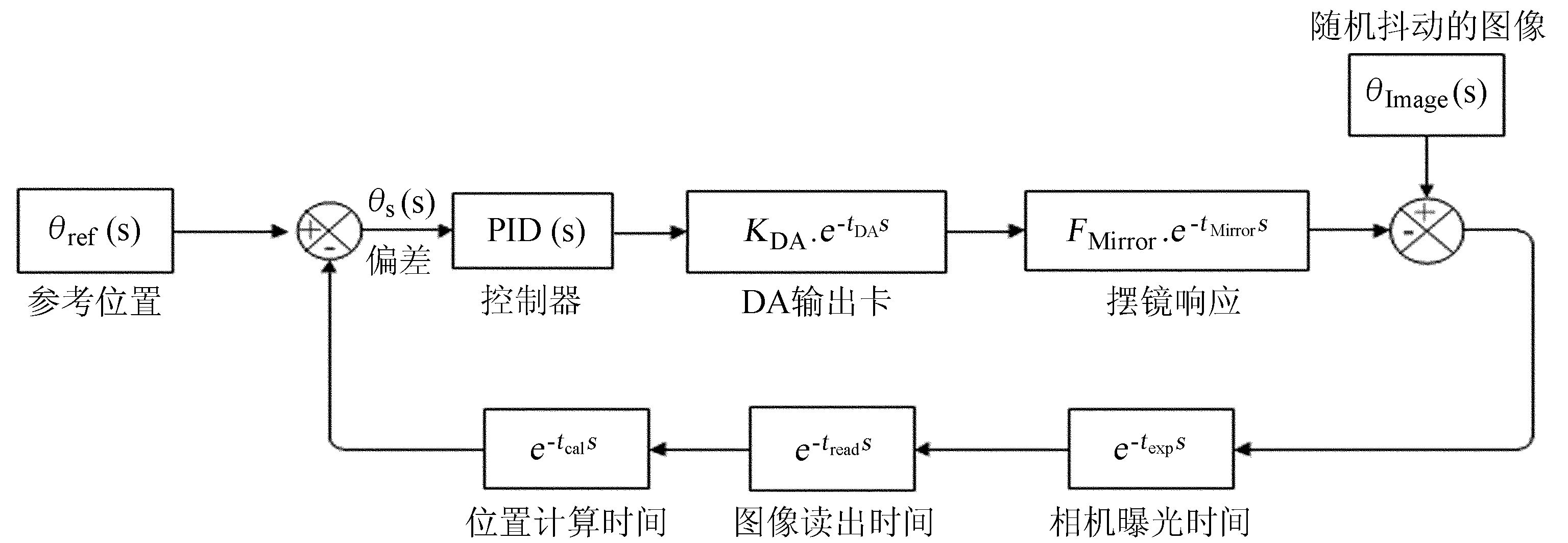
3 摆镜图像稳定闭环控制系统的数值模拟 3.1 摆镜图像稳定闭环控制系统传递函数的建立根据图 2摆镜图像稳定闭环控制系统的控制原理图,用传递函数表示每个环节,可以得到控制系统的传递函数框图,如图 5。从该图可以看出,系统主要包括PID控制器、系统延迟环节、系统比例环节和被控制对象(摆镜系统)环节。除被控对象摆镜外,其它每个环节的传递函数都容易得到。因此,摆镜图像稳定控制系统的传递函数主要先确定被控对象摆镜系统的传递函数。
|
| 图 5 摆镜闭环控制系统的传递函数框图 Fig. 5 The block diagram of the transfer function for the closed-loop control system of the tip-tilt mirror |
在测试摆镜系统的阶跃响应动态特性时,系统有一个小的延迟,在微秒量级,在1V和10V的阶跃响应特性中,压敏电阻的反馈电压(或者摆镜的转动角)随时间成线性变化,是一个斜坡响应,传递函数可以简化为以下模型:
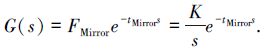
通过实验,摆镜系统的延迟时间tMirror与控制电压的幅度无关,且平均值在60μs左右,因此tMirror等于6×10-5s。斜率K代表摆镜转动角随时间的变化速度,根据图 4(b)和4(c)中1V和10V的阶跃响应以及转角电压响应(1)和(2)式,以角秒/毫秒为单位,不难求出KX和KY。因此,摆镜系统在两个正交方向的传递函数为
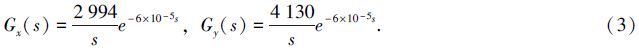
摆镜闭环控制系统中,延迟环节主要包括5个,数字信号转模拟信号的延迟几微秒,摆镜延迟tMirror为60μs,相机曝光时间几毫秒,图像的读出时间和计算时间与图像的大小有关,如果以TiO通道的CCD像素比0.05446″/pixel,当望远镜工作在6级风,则图像大小应该在300×300,此时,实测CCD图像读出时间需要13.16ms,图像重心计算时间0.689ms。因此,如果将系统的延迟环节进行合并,系统总延时在20ms左右。
3.2 摆镜图像稳定闭环控制系统的数值模拟对控制系统的数值模拟,主要根据控制系统的传递函数设计相应的控制器,分析系统参数变化时控制系统性能的变化,最终确定控制系统的比例积分微分控制器参数、系统延迟参数和控制带宽等重要指标。数值模拟时,图像抖动随时间的变化为图 3的实测数据,摆镜的传递函数为(3)式。数值模拟的方法是根据系统传递函数进行离散变换,然后编写matlab程序进行数值模拟。比例积分微分控制器参数主要根据系统的阶跃响应曲线确定,标准为上升时间、调整时间和峰值时间都应该达到最小,同时将最大超调量控制在20%以内。系统控制性能评价指标为摆镜改正后图像抖动的均方根值。
比例积分微分控制器采用(4)式的传递函数:
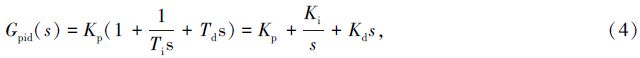
| 序号 | X方向 | Y方向 | ||||||||
| Kp(×10-2) | Ki(×10-3) | Kd(×10-4) | 超调量/% | 误差均方根/″ | Kp(×10-2) | Ki(×10-3) | Kd(×10-4) | 超调量/% | 误差均方根/″ | |
| 1.1 | 0 | 0 | 17.25 | 0.4623 | 0.8 | 0 | 0 | 17.44 | 0.5455 | |
| 1 | 1.2 | 0 | 0 | 22.85 | 0.4380 | 0.9 | 0 | 0 | 25.23 | 0.5028 |
| 1.3 | 0 | 0 | 28.63 | 0.4176 | 1 | 0 | 0 | 33.31 | 0.4679 | |
| 1.2 | 1 | 1 | 20.35 | 0.4354 | 0.9 | 1 | 1 | 21.75 | 0.4968 | |
| 2 | 1.2 | 1 | 3 | 15.16 | 0.4296 | 0.9 | 1 | 3 | 14.74 | 0.4929 |
| 1.2 | 1 | 4 | 12.73 | 0.4272 | 0.9 | 1 | 4 | 11.54 | 0.4907 | |
| 1.2 | 1 | 5 | 10.39 | 0.4252 | 0.9 | 1 | 5 | 8.81 | 0.4893 | |
| 1.3 | 1 | 1 | 26.04 | 0.4151 | 1 | 1 | 1 | 29.74 | 0.4653 | |
| 3 | 1.3 | 1 | 3 | 20.75 | 0.4098 | 1 | 1 | 3 | 22.67 | 0.4603 |
| 1.3 | 1 | 4 | 18.29 | 0.4077 | 1 | 1 | 4 | 19.72 | 0.4589 | |
| 1.3 | 1 | 5 | 15.94 | 0.4060 | 1 | 1 | 5 | 17.13 | 0.4585 | |
| 1.3 | 1.1 | 4 | 18.31 | 0.4078 | 1 | 1.1 | 4 | 19.75 | 0.4590 | |
| 4 | 1.3 | 0.9 | 4 | 18.27 | 0.4076 | 1 | 0.9 | 4 | 19.71 | 0.4589 |
| 1.3 | 0.8 | 4 | 18.24 | 0.4076 | 1 | 0.8 | 4 | 19.68 | 0.4588 | |
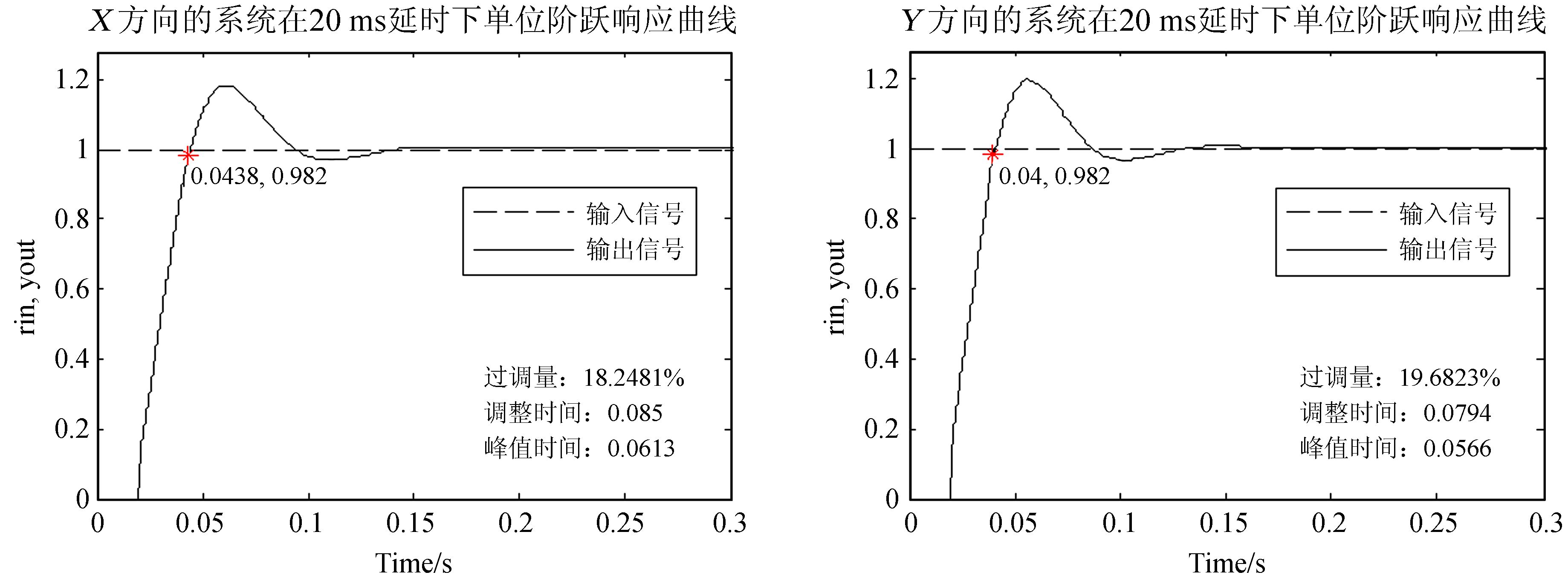
从表 2可以看出,X方向的误差均方根值在Kp=0.013、Ki=0.001、Kd=0.00005时最小,Y方向的误差均方根值在Kp=0.01、Ki=0.001、Kd=0.00005时最小,但此时两方向的单位阶跃响应曲线不再光滑。通过第4组数据发现,增大Ki会增加误差的均方根值,减小Ki会减小误差的均方根值,而在Ki从0.001变化到0.0008时,均方根值的减小程度已不大,因此选择另一个均方根值接近最小值的一组比例积分微分参数:X方向Kp=0.013、Ki=0.0008、Kd=0.00004,Y方向Kp=0.01、Ki=0.0008、Kd=0.00004,且两组参数下的单位阶跃响应的超调量不超过20%。两个方向的单位阶跃响应曲线如图 6。
|
| 图 6 延迟时间为20ms时的系统单位阶跃响应特性曲线 Fig. 6 The unit step response curve of the system at the defer time of 20ms |
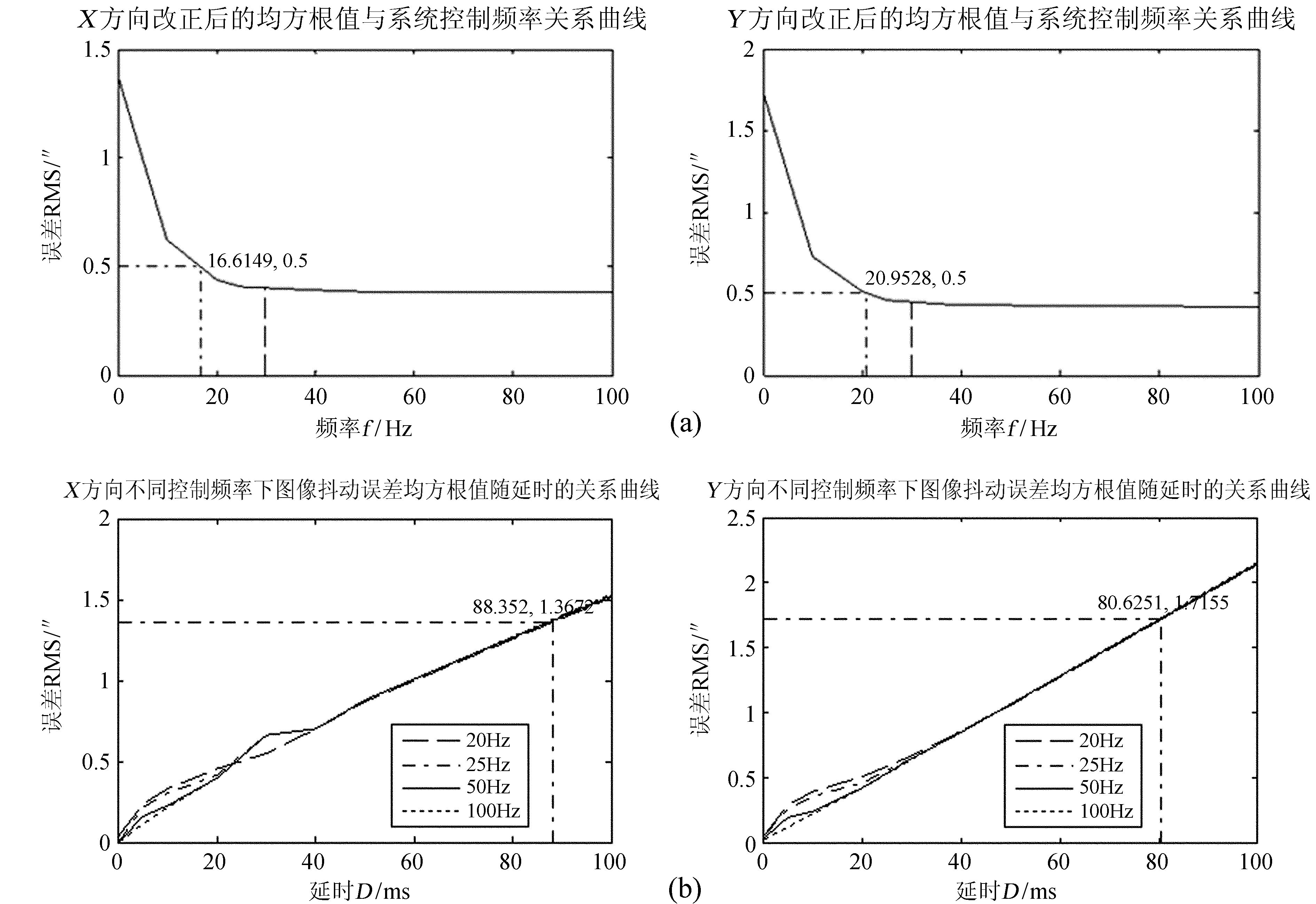
由于不同系统延迟时间和不同控制频率需要采用不同的比例积分微分控制参数,才能得到控制系统误差的最小均方根值。当系统延迟时间固定在20ms时,图像改正后的均方根值随系统的控制频率变化,如表 3或图 7(a)。当系统的控制频率固定后,图像改正后的均方根值随系统的延迟时间变化。图 7(b)给出了控制频率固定为20Hz、25Hz、50Hz、100Hz时,均方根值随系统延迟时间变化的曲线。
| 频率/Hz | X方向误差 | Y方向误差 | ||
| RMS/″ | PV/″ | RMS/″ | PV/″ | |
| 10 | 0.6192 | 8.5611 | 0.7234 | 9.1021 |
| 20 | 0.4390 | 4.9738 | 0.5097 | 4.7752 |
| 25 | 0.4076 | 4.6020 | 0.4588 | 4.3021 |
| 40 | 0.3869 | 4.2827 | 0.4292 | 3.8969 |
| 50 | 0.3849 | 4.3865 | 0.4239 | 4.0874 |
| 100 | 0.3836 | 3.9644 | 0.4205 | 3.5931 |
|
| 图 7 (a) 系统20ms延时下闭环控制后的图像抖动的均方根值随控制频率的变化曲线;(b) 控制系统在不同控制频率下图像抖动的均方根值随延时变化曲线 Fig. 7 (a) The curve of the image vibration RMS value with the frequency change at the defer time of 20ms; (b) The curve of the Image vibration RMS value with the defer time change in different control frequencies for the control system |
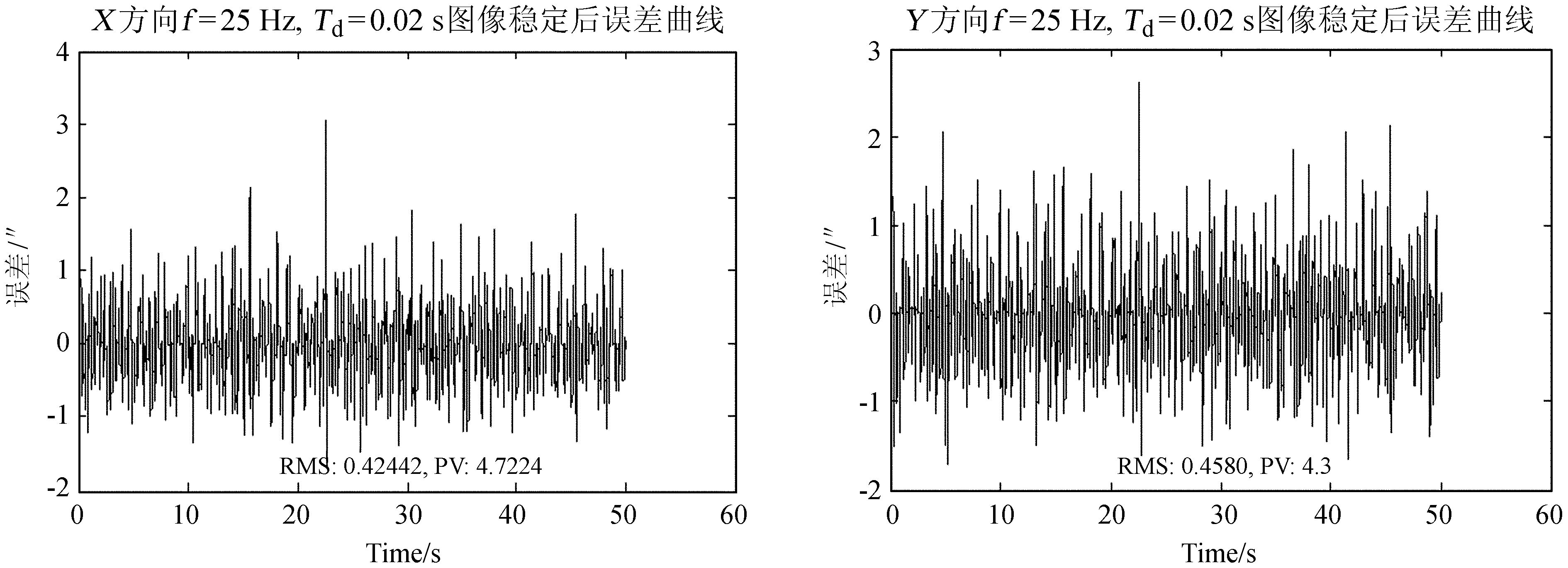
结合表 3和图 7(a):在20ms的系统延迟下,在0~30Hz频率范围内,随着控制系统的频率增加,控制系统的性能越好,当频率超过30Hz时,提高控制系统的频率,系统的性能改善并不明显。从表 3还可看出,当控制系统X、Y方向的系统频率设置在25Hz时,图像抖动(或者闭环系统的误差)均方根值小于0.5″。从图 7(b)可以看出:摆镜的X、Y两个方向在不同控制频率下,图像稳定后的误差均方根值随延迟时间的变化规律是在延迟小于40ms时,随控制频率的增加有所改善,在延迟大于40ms后,提高控制频率,均方根值基本不变。总体来讲,随着延迟时间的增加,各个控制频率下的图像稳定后的误差均方根值都会增加。从图中标注可以看出:当X方向的延迟时间超过88.352ms,Y方向的延迟时间超过80.6251ms时,改正效果比改正之前的更差。因此,在控制系统闭环时,系统在两个方向上的延迟不能超过以上两个值。根据上述结果,图 8展示了控制频率25Hz、延迟时间20ms下的摆镜闭环控制系统对图像稳定后的抖动误差随时间的变化曲线。
|
| 图 8 控制系统在控制频率25Hz和延时20ms时稳像后的模拟误差曲线 Fig. 8 The stabilization simulated error curve with the control frequency of 25Hz and the defer time of 20ms |
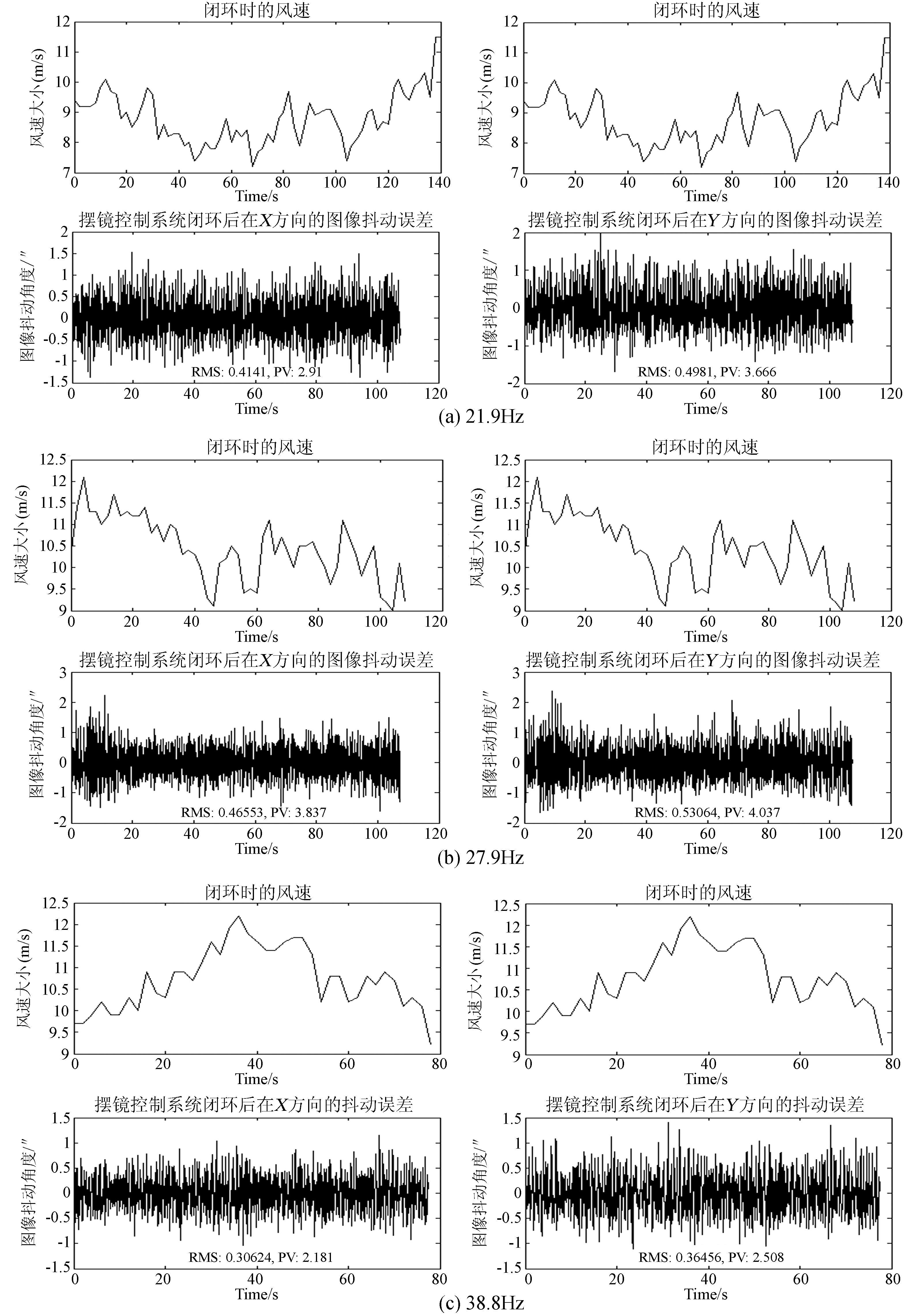
根据数值模拟,开展摆镜图像稳定控制系统闭环实验,实验选择在风速较高时进行,观测目标为星,移开1m太阳望远镜的风障板,让1m太阳望远镜全部暴露在风中,并且镜筒迎风而向,使其受风的影响最大。当系统工作在开环时,对应风速下图像抖动如图 3,当摆镜控制系统闭环后,并且控制频率分别工作在21.9Hz、27.9Hz和38.8Hz时,得到对应风速下的图像抖动如图 9(a)、 (b)、 (c),闭环后图像抖动随时间的变化如表 4。
|
| 图 9 摆镜闭环控制系统分别在21.9Hz、27.9Hz、38.8Hz时的实测图像抖动误差曲线 Fig. 9 The image measured jitter error curves for the closed-loop control system of the tip-tilt mirror working at 21.9Hz,27.9Hz,38.8Hz |
| 频率f/Hz | X方向的误差RMS/″ | Y方向的误差RMS/″ |
| 21.9 | 0.414 | 0.498 |
| 27.9 | 0.466 | 0.531 |
| 38.8 | 0.306 | 0.365 |
从表 4可以看出,随着摆镜控制频率的增加,图像抖动(闭环控制误差)的均方根值随之减小,20Hz也达到较为理想的结果。当然,实验时,图像闭环控制误差的均方根值变化并不完全取决于摆镜闭环控制频率,它受实验时的风速、风向的变化以及风与望远镜作用的方向等因素的影响。
5 结 论本文通过数值模拟分析,当1m太阳望远镜工作在五到六级风的情况下,摆镜图像稳定控制系统的系统延迟时间在20ms,系统闭环控制频率只要工作在25Hz左右,就能将图像抖动的均方根值控制在0.5″以内。经过多次实验证明,这一结论是成立的。因此,采用芯明天公司型号为XS-340.4SL二维摆镜建立图像稳定闭环控制系统以稳定随机风载对1m太阳望远镜引起的焦面图像抖动方法是可行的。
| [1] | Liu Zhong,Xu Jun.1-meter near-infrared solar telescope[C]//Choudhuri A R,Banerjee D.First Asia-Pacific Solar Physics Meeting ASI Conference Series.2011:9-17. |
| [2] | 王瑞,徐稚,刘忠.一米新真空红外太阳望远镜多波段光谱仪光谱弯曲分析[J].天文研究与技术——国家天文台台刊,2014,11(2):165-167.Wang Rui,Xu Zhi,Liu Zhong.An analysis of spectrum curvatures for the multi-wavelength spectrometer of the new vaccum solar telescope of the Yunnan Observatories[J].Astronomical Research and Technology——Publications of National Astronomical Observatories of China,2014,11(2):165-167. |
| [3] | 李志,宋腾飞,许骏.阻导风板及其在NVST上的测试结果[J].天文研究与技术——国家天文台台刊,2012,9(3):329-334.Li Zhi,Song Tengfei,Xu Jun.A set of H-S windscreens and test results of it on the YNAO NVST[J].Astronomical Research and Technology——Publications of National Astronomical Observatories of China,2012,9(3):329-334. |
| [4] | 柳光乾.一米红外太阳望远镜控制系统研制[D].云南:中科院云南天文台,2011. |
| [5] | 柳光乾,程向明,宋腾飞,等.一米太阳望远镜风载对伺服系统的影响及控制[J].光电工程,2011,38(6):50-58.Liu Guangqian,Cheng Xiangming,Song Tengfei,et al.The infuence and control of wind loading on the one meter solar telescope servosystem[J].Opto-Electronic Engineering,2011,38(6):50-58. |
| [6] | 赵艳彬,许域菲,廖鹤,等.压电偏摆镜快速精确控制研究[J].空间控制技术与应用,2014,40(2):31-36.Zhao Yanbin,Xu Yufei,Liao He,et al.On fast and accurate control for piezo-based steering mirro[J].Aerospace Control and Application,2014,40(2):31-36. |
| [7] | 韩诚山,李祥之,文明,等.基于压电偏转系统的卫星平台振动补偿[J].光学精密工程,2011,19(9):2085-2091.Han Chengshan,Li Xiangzhi,Wen Ming,et al.Vibration compensation of satellite platform based on piezo-eletric steering system[J].Optics and Precision Engineering,2011,19(9):2085-2091. |
| [8] | 徐飞飞,纪明,赵创社.快速偏转反射镜研究现状及关键技术[J].应用光学,2010,31(5):847-850.Xu Feifei,Ji ming,Zhao Chuangshe.Status of fast steering mirror[J].Journal of Applied Optics,2010,31(5):847-850. |
| [9] | 黎明,黄勇.16KM空间光通信的跟踪实验研究[J].仪器仪表学报,2011,32(1):230-234.Li Ming,Huang Yong.Experimental study of tracking system for 16km free-space optical communication[J].Chinses Journal of Scientific Instrument,2011,32(1):230-234. |
| [10] | 谭立英,吴世臣,于思源,等.潜望式光通信终端反射镜安装误差补偿方法研究[J].载人航天,2011,16(3):54-57.Tan Liying,Wu Shichen,Yu Siyuan,et al.Compensating algorithm of setting errors of reflex mirror in periscope intersatellite optical communication terminal[J].Manned Spaceflight,2011,16(3):54-57. |
| [11] | 吴松涛.导弹预警系统二维摆镜结构及其控制系统研究[D].哈尔滨:哈尔滨工业大学,2006. |
| [12] | Germann L M,Braccio J.Fine-steering mirror technology supports 10 nanoradiansystems[J].Optical Engineering,1990,29(11):1351-1359. |
| [13] | 曲蔚然,林岩,刘洛霞.基于扫描反射镜的惯性稳像控制系统设计[J].电光与控制,2013,20(9):69-73.Qu Weiran,Lin Yan,Liu Luoxia.Design of an inertial Image stabilization control system based on scan mirror[J].Electronics Optics & Control,2013,20(9):69-73. |
| [14] | Wang Rui,Xu Zhi,Jin Zhenyu,et al.The first observation and data reduction of the Multi-wavelength Spectrometer on the New Vacuum Solar Telescope[J].Research in Astronomy and Astrophysics,2013,13(10):1240-1254. |


