1 Introduction

Most of Earth’s major features can be understood from the interactions between tectonic plates,which move independently,separating from,colliding with,and sliding against one another. Until the middle 1960s an unifying theory was developed to explain Earth’s dynamics^[1]. Several decades after the inception of the theory on plate tectonics,the plate dynamic models constructed using the geological and geophysical data have been dominant,until long time-span geodetic observations were gathered to estimate contemporary plate kinematic parameters^{[2, 3, 4, 5]}. As one of the most representative geological plate motion models,NUVEL-1A is one of the mainstream models regarding the plate dynamics and kinematics. With the setting up of the enhanced amount and quality of the geologic or geodetic data during the last few years,the MORVEL refined the precision and accuracy of the geometric and kinematic parameters for 56 plates that are partly taken from an updated digital model of pate boundaries by Bird^[6]. Relative to the NUVEL-1A,the MORVEL incorporates more than twice as many plates and covers more of Earth’s surface,and nearly all the NUVEL-1A angular velocities differ significantly from its MORVEL counterparts^[7].

To derive an absolute motion model in a NNR reference frame,however,the inertia tensors are always considered as indispensable attribute of all these plates. Despite various established methods for calculating plate inertia tensors corresponding to the NUVEL-1A model presented in many papers^{[8, 9]},however it is necessary to recalculate a new set for the NNR-MORVEL56 model^[10],given the considerable discrepancy between the NUVEL-1A and the MORVEL.

When a polygon on the unit sphere is employed for the representation of a tectonic plate,a simplified analysis of the plate inertia tensor can be performed through a numerical method,which is carried out over all 56 plates. The method for calculating all 9 components of the inertia tensor is illustrated in this paper and this method requires the precise knowledge of the plate boundaries. The boundary file contains a 2-column sequence of the latitude-longitude plate boundary coordinates that fully enclose the plate in the counterclockwise direction.

In the first section,we introduce some concepts regarding the no-net-rotation conditions and indicate the calculation of the Euler vector in an absolute motion model. The following section describes the detailed mathematical models to estimate the area and the inertia tensor of the spherical polygons. The last section of this paper is dedicated to manifest the results for 56 modern plates and the appendix gives the original FORTRAN90 program for obtaining the aforementioned results.

2 Net Lithosphere Rotation

A no-net-rotation model for the lithosphere assumes that the integral of v×r over the Earth’s surface equals zero^[11],i.e.

where,r is the radial vector of the surface element on a unit sphere,and v corresponds to the horizontal velocity at that position. The angular velocity of net rotation ω_net was computed as the total angular momentum of all plates divided by the moment of inertia of the entire lithosphere,using the equation^{[12, 13]} Then it is convenient to convert the Eq.(2) into the following form^[8]: where ω_i is the Euler vector describing the motion of plate i relative to an inertial reference frame,such as ITRF2008,and Q_i is the inertia tensor of plate i,where i goes from 1 to n. The angular velocities of the plates relative to the NNR reference frame were then found by vector subtraction,namely, For those tectonic plates where angular velocities are not available in the geodetic model such as the ITRF2000-PMM,due to a lack of sufficient data,Altamimi^[14] tested four cases to perfect the incomplete geodetic model. The fourth case described a method for estimating the missing angular velocity. Here we employ it in this paper by using a simple equation written as: where ω_i^ITRF is the undetermined rotation vector of plate i in the ITRF model,and ω_ij^MORVEL is the MORVEL rotation vector for plate i relative to plate j,which is adjacent to the missing plate i.

3 Area and inertia tensor of plates 3.1 Evaluation of the plate area

The spherical polygons are defined by great circle arcs connecting points on the sphere,the positions of which are given by latitudes and longitudes. In fact,an algorithm for determining the area of a spherical polygon of arbitrary shape has been presented by Bevis and Cambareri^[15],where the kernel idea is to compute the interior angle at each vertex of the spherical polygon. In this paper,however,we employ a somewhat similar method to that of Miller^[16],trying to determine the area of spherical polygon by summing the signed areas of component triangles.

For a spherical polygon of n sides,the spherical excess E is generalized as

where α_i(i=1…n) are the interior angles of the polygon. Considering a spherical polygon ABCD as shown in Fig. 1(a),the north-pole combined with any two adjacent vertices of the polygon can constitute a spherical triangle,such as NAB. The two sides of the triangle are known from the latitudes of their vertices,i.e. an=π/2-latitude(A) and bn=π/2-latitude(B). Taking the previously obtained two sides and the included angle specified by the difference between longitudes of A and B,the opposite side ab can be calculated via the formula: where the haversine function is defined as havx=(1-cosx)/2 with x in radians. Having obtained all three sides of the spherical polygon,we can use the formula to obtain its excess: where s=${{an + bn + ab} \over 2}$.

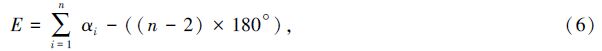
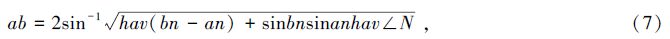
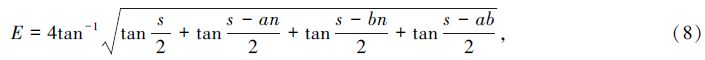
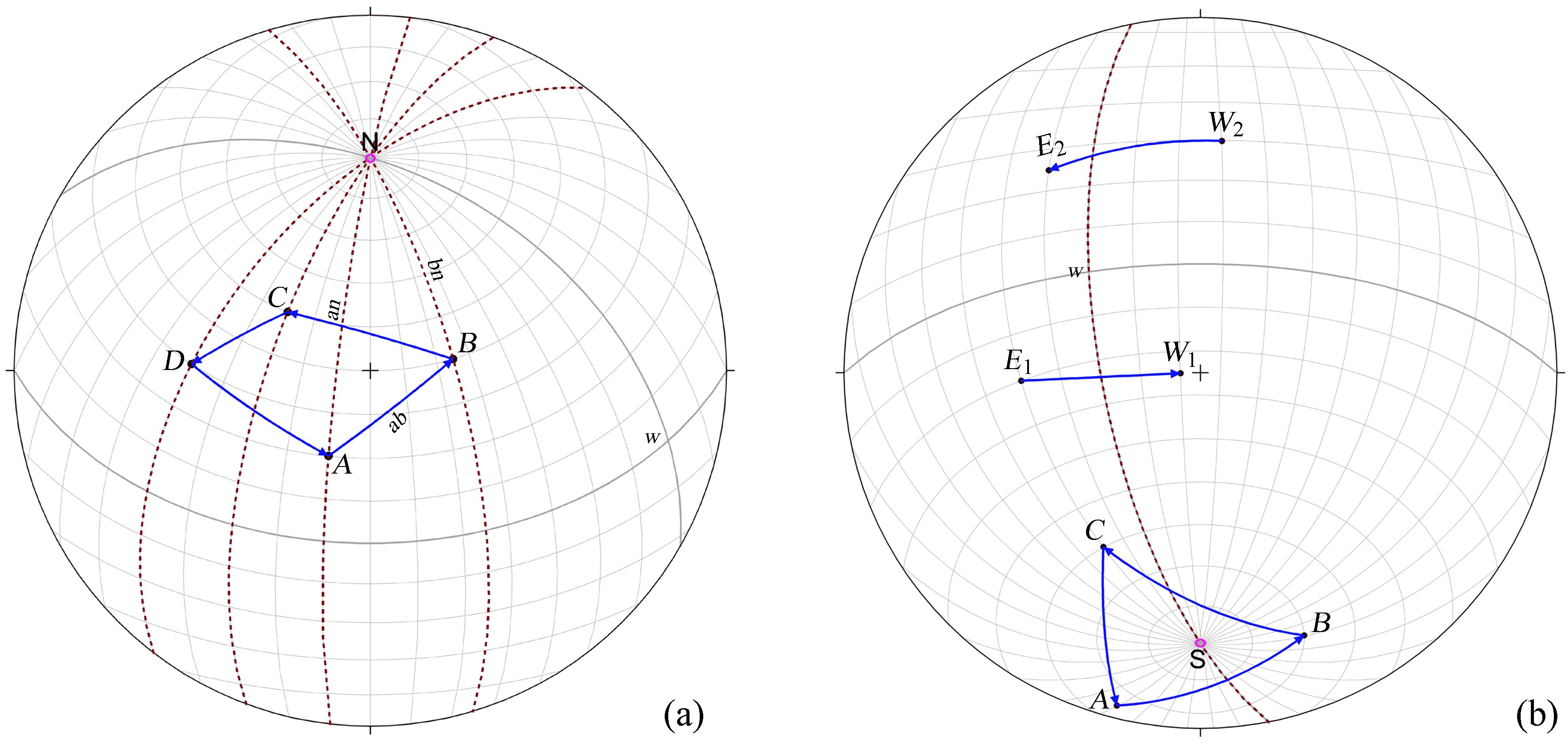
To find the area of a spherical polygon,first,one may use the successive vertices in pair to form a spherical triangle. Each spherical triangle employs the north pole as a common vertex to make the calculations convenient. When calculating the areas of the individual triangles,we adopt a convention that the sign of the triangle area(which has a same value as the spherical excess for a polygon on a unit sphere) is identical to the sign of the difference between the longitudes of a pair of adjacent vertices. If the longitude of the first vertex is less than the second one,then the sign of this triangle area is defined as a positive value for a set of points arranged in the anticlockwise way and vice versa. Therefore the area of the spherical polygon isregarded as the absolute value of the sum of the signed spherical excesses for each of the spherical triangles. Taking the facility of the calculation for the upcoming inertia tensor,a provision is crucial that the vertex point traversing the polygon prefersto be enumerated in the counterclockwise direction.

One should note the following two special cases when estimating the geometric parameters of the spherical polygons. The first case is as follows: if the sides of the polygon cross over the International Date Line from point E₁ to W₁,as illustrated in the Fig. 1(b),a 2π has to be added to the longitude of W₁. The same applies to a similar situation when a vertex leave W₂ for E₂,a 2π has to be subtracted from E₂ in order to promise the continuity of the calculation. The second case occurs when a spherical polygon has an area larger than that of the hemisphere. According to a implicit assumption that the area of any polygon is less than 2π,for those extensive polygons,such as the triangle ABC surrounding the north pole N,the exact area of ABC is the complement of ABC including the north pole,i.e. Exactarea=Area_ABC^S=4π-Area_ABC^N. The original FORTRAN90 program in the appendix has taken into account these two singular cases.

3.2 Estimation of plate inertia tensor

The components of the symmetric inertia tensor Q can be calculated for a region P using the following formula:

where x_μ(μ=1,2,3) are the Cartesian coordinates,δ_μν(μ,ν=1,2,3) are the elements of the identity matrix,and the integration is carried out over the surface of a plate P. These inertia tensors are based on the hypothesis that the surface density of the plate is unit one,and entirely describe the plate geometry. For instance,the plate area A is easily calculated by taking the trace of Q: This implies invariance of the trace under coordinate rotations and the sum of the diagonal components is always double the area of the polygon. Generally speaking,non-diagonal components indicate the asymmetry of the polygon with respect to the Cartesian axes,and all of the diagonal components have a positive value,which is useful,together with the Eq.(10),as the verification test for the calculation results.

In this paper we propose a somewhat different method from Schettino^[17] for constructing the spherical triangle. In fact,we will see that the integral at the right-hand side of (Eq.(9)) is easily calculated for spherical triangles. The components of the total tensor are therefore given by:

where A is the total polygon area,which has been illustrated in the last section. Let a point on the sphere be given in spherical coordinates (θ,λ),where θ is the latitude and λ is the longitude,so that its Cartesian coordinates are given by then the area element dA at this position is equal to cosθdλdθ. The components of the inertia tensor for a triangle NAB are therefore written,in spherical coordinates,as: where λ₁,λ₂ are the longitudes of vertices A,B and the function f is given by Next,as a result of the symmetry of the inertia tensor,the 6 independent components of f are expressed in the following way: The upper limit of the inner integral about the latitude is always set to π/2,because the North Pole is considered as the common vertex of each of the spherical triangles. In contrast,with the simple upper limit,the lower limit function θ(λ) can be obtained from a serious of derivations,whose concrete form is formulated as where C₁,C₂,C₃ represent three constants. Once the integrated triangles are determined by one side of the polygon,such as AB,we can write their expression in the following form: where (θ₁,λ₁),(θ₂,λ₂) are the latitude and the longitude of vertices A and B,respectively.

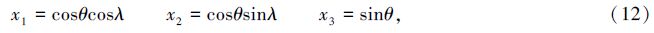
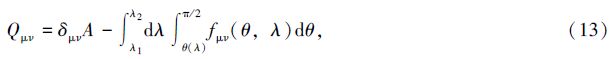
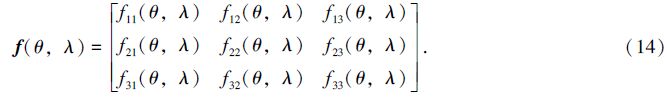
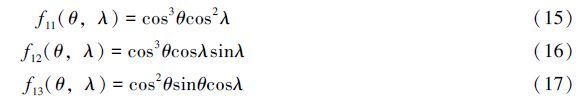
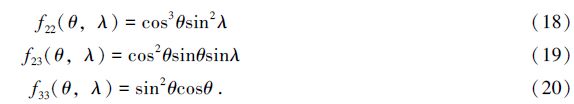
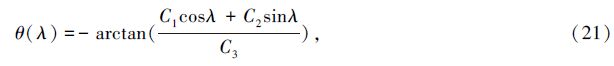
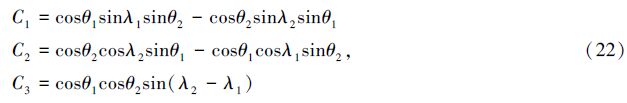
Unlike the process of the area estimation,the evaluation of the inertia tensor is associated with the integral order. Hence,a counterclockwise direction must be adopted in the procedure. All of the special situations have been considered in the Fortran program,including the 180th meridian case and the encompassing the South Pole case. In addition to the aforementioned two special cases in the area estimation,the principal moments in the tensor calculation need to be deducted from the whole inertia tensor of the spherical surface in order to acquire the exact moments,i.e. Moment_Exact^S=8π/3-Moment_Principal^N,when involving the polygon containing the south pole.

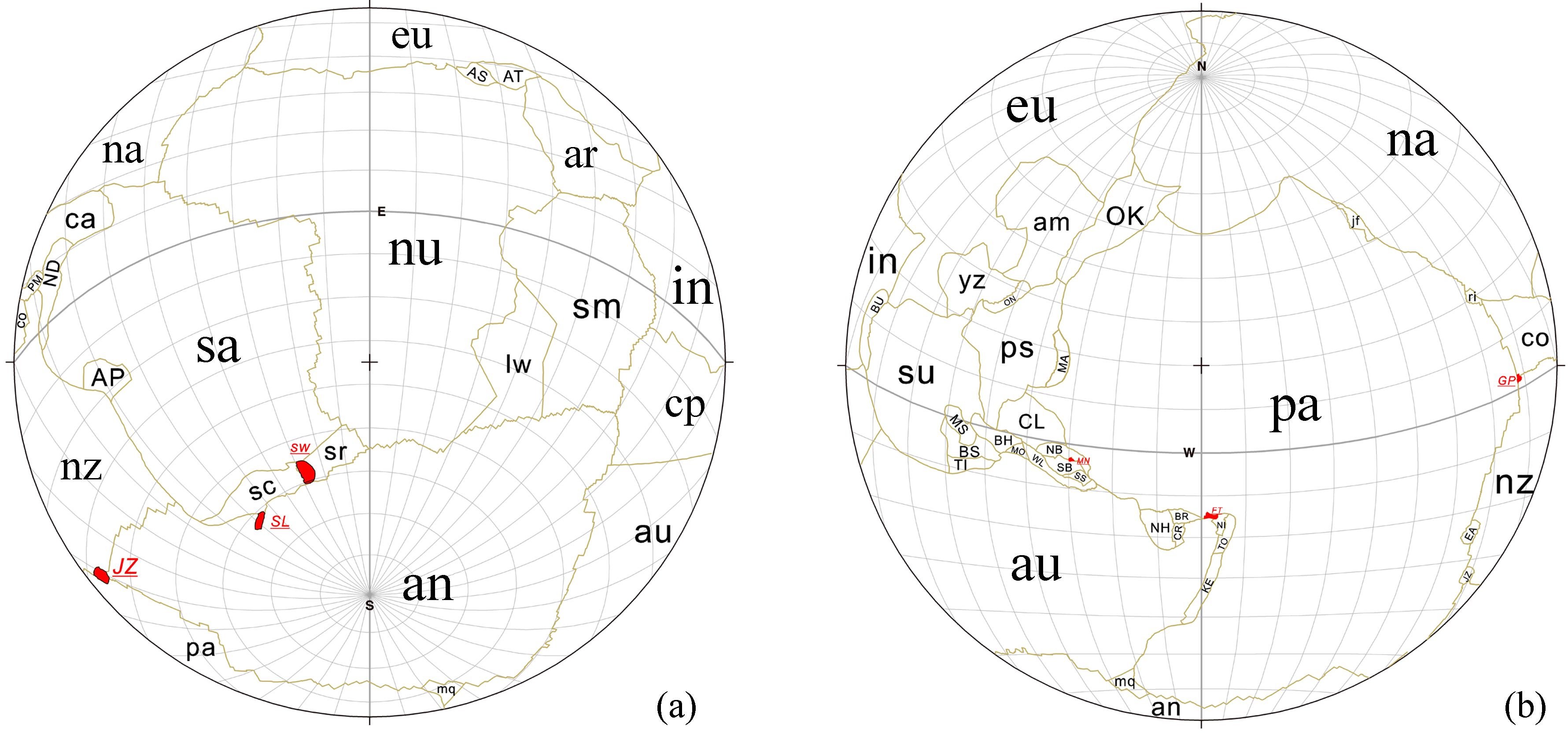
4 Results and analysis

The NNR-NUVEL56 model contains 56 tectonic plates around the earth,and the software OSXStereonet developed by Cardozo and Allmendinger^[18] was applied to plot the global plate distribution map,as illustrated in Fig. 2. Utilizing the Fortran program,we estimated geometry parameters of all 56 modern plates with the accuracy the inertia tensor better than 10^-6. Table 1 lists the area and the inertia tensor of all MORVEL plates,which provide essential material for calculating plate kinematic parameters in the NNR reference frame. The sum of the area of all plates equals 12.566340 steradian,which is slightly less than the surface area of the whole unit sphere,namely 4π(12.566371) with the relative error η=0.00023%. Our results indicate that the relative errors for the six components of the total tensor are 0.00017%,0.00029%,0.00026%,0.0010%,0.00016%,and 0.00010% respectively,It is shown that the inertia tensor of the entire spherical surface is 8π/3E,where E takes the identity matrix. The discrepancy probably arises from either the imperfection of plates over the entire sphere or the unavoidable rounding errors in floating point arithmetic.

5 Conclusion

The method for computing the areas and inertial tensors of tectonic plates has been presented. This method is based upon the triangulation algorithm and the adaptive Simpson’s double integral procedure,which can be applied to the spherical polygons representing such tectonic plates. Results for the NNR-MORVEL56 tectonic plates show that highly reliable data can be produced,as long as starting from the precise definition of the plate boundaries. In addition,a FORTRAN90 program has been attached to the end of thispaper,which is expected to be valuable to the future studies of the kinematics and dynamics associated to the motions of tectonic plates.

The FORTRAN90 Program