2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
弱引力透镜被认为是探测暗能量的一种强有力的工具,它通过探测遥远星系图像的切变来研究暗能量的性质及其他宇宙学参数。很多大型巡天望远镜(如LSST①(① http://www.lsst.org/lsst/)、EUCLID②(② http://sci.esa.int/euclid)、WFIRST③(③ http://wfirst.gsfc.nasa.gov/))把弱引力透镜作为探测暗能量的重要手段。由于弱引力透镜的信号极其微弱,为了提取有用信息,未来的大型弱引力透镜项目需要探测大量的星系红移样本,以至于探测全部样本的光谱红移在时间上是不可能的。因此,必须用多色测光的方法估计红移,而测光红移通过多波段成像,利用经验公式[1, 2]、能谱分布(Spectral Energy Distribution,SED)模板拟合[3]、人工神经网络[4]等方法估计红移。对宇宙学有用的是星系的红移分布,而不是每个星系的红移。通过抽样测量星系的真实红移或者利用宇宙学方法可以校正测光红移误差分布[5, 6, 7, 8]。但是红移分布的不确定性不可避免地传递到暗能量状态方程参数及其他宇宙学参数上[9, 10]。研究表明,若所有在真实红移区间为0.1的星系的测光红移误差分布都可用一个平均值在真实红移附近的高斯分布近似,则需要104到105的光谱红移校正,才使得暗能量的误差放大限制在1.5倍以内[9]。其次,由于星系能谱分布中的谱线特征信息混淆或者波段缺乏特征信息,导致估计的测光红移对真实红移出现较大的偏离④(④ Yee H K C. Photometric redshift techniques: reliability and applications),即所谓灾难性测光红移。特别是红移约小于1的星系能谱分布中的巴尔莫跳变(Balmer break)和红移约大于2的星系能谱分布中的拉曼跳变(Lyman break)的混淆导致局域性的灾难性测光红移[11]。灾难性测光红移的存在使弱引力透镜对暗能量状态方程参数的估计产生偏差[11, 12, 13]。对于灾难性的测光红移,可以通过剔除一些灾难性红移可能性较大的样本,从而在一定程度上减少灾难性红移导致的系统误差的同时又不会过多地增加因减少样本而导致的统计误差[13, 14]。
星系功率谱(或星系关联函数)中的重子声波振荡包含了在最后散射截面的声波视界(标准尺)的信息。利用标准尺可以测量哈勃参数-红移关系及角直径距离-红移的关系[15]。在多色成像巡天中,仅靠重子声波振荡测量的多个红移处的角直径距离对暗能量状态方程参数的限制有较大的简并性[16]。此外,由于星系偏袒因子的不确定性,使得难以从星系角功率谱中抽取更多的信息[17, 18]。
由于重子声波振荡和弱引力透镜的互补效应,当把星系与弱引力透镜的交叉功率谱也考虑进来时,在没有灾难性测光红移的情况下,一方面弱引力透镜可以帮助校正星系偏袒因子,另一方面不同的测光红移区间的星系交叉角功率谱对测光红移的误差分布非常敏感,从而对测光红移误差分布参数具有很强的自校正作用,联合重子声波振荡和弱引力透镜也能使测光红移偏差δz得到更强的限制[19]。
本文研究由于存在局域性的灾难性测光红移但没有把它们纳入拟合的模型而导致暗能量状态方程参数在重子声波振荡和弱引力透镜单独以及联合限制下的估计偏差。然后探讨把灾难性测光红移纳入拟合模型后重子声波振荡和弱引力透镜的互补效应和对暗能量状态方程参数的限制能力。
本文第1节主要介绍星系功率谱和弱引力透镜功率谱,包括局域性的灾难性测光红移在内的测光红移误差分布的模型,以及误差估计的方法——费舍尔矩阵;第2节给出本研究的预测结果;第3节是本文的结论。
1 方 法 1.1 观测量:功率谱以星系的角功率谱、弱引力透镜的角功率谱以及它们的交叉功率谱作为观测量。在林伯(Limber)近似[20, 21]下,星系和弱引力透镜的角功率谱可以写为[19]
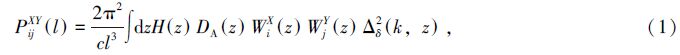
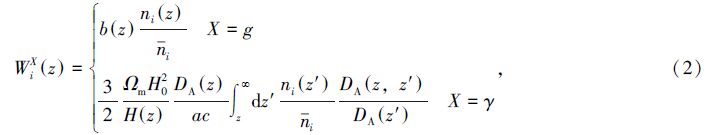
在实际观测中,由于星系角功率谱受到星系散粒(形状)噪声ni-1的影响,弱引力透镜角功率谱则受到固有形状噪声γrms2ni-1的影响,因而观测的功率谱为

本文用CAMB[22, 23]输出不同红移处的非线性物质功率谱(基于Halofit模型[24]的修正[25]),具体使用参考CAMB主页⑤(⑤ http://camb.info)。
1.2 模型与巡天属性模型参数包括10个宇宙学参数,31个星系偏袒因子,60个测光红移误差分布参数。当把灾难性测光红移加入拟合模型时,会增加45个灾难性测光红移误差分布参数。
1.2.1 模型在没有灾难性测光红移的情况下,每一个测光红移区间的真实红移分布用高斯函数描述。如果存在灾难性测光红移,则可相应多加一个高斯函数描述灾难性测光红移的真实红移分布。
假设巡天的测光红移分布是n(zph),对测光红移空间平均分成N个区间,在没有灾难性测光红移的情况下,第i个区间星系的真实红移分布可用高斯分布近似:
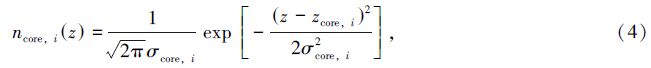
存在灾难性测光红移的情况下,任意区间的真实红移分布可用两个高斯分布的叠加近似,分别用于描述核心(真实红移附近)部分和灾难性测光红移部分的真实红移分布:
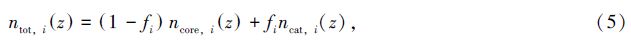
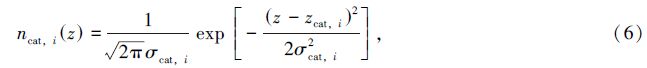
参照[9, 19],把测光红移为0到3的区间均匀分成30个子区间,即N=30,每个子区间宽为0.1。zcore,i和σcore,i的基准值取:
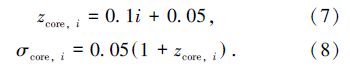
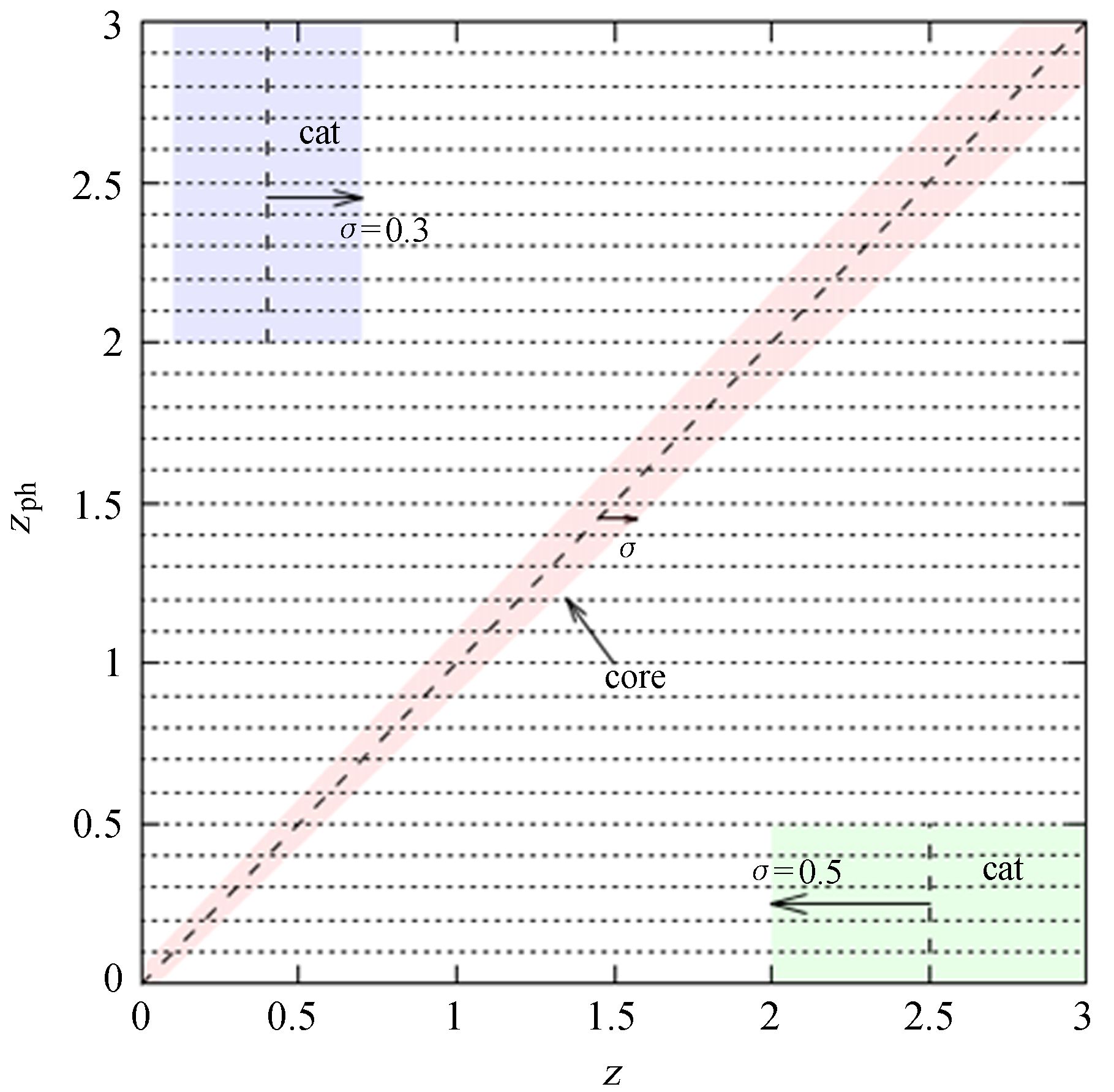
由于光谱特征的混淆或者光谱缺乏信息量等原因,测光红移的估计会出现灾难性的错误,特别是当光谱上的拉曼跳变和巴尔莫跳变混淆时,会在z-zph面的左上角和右下角分别出现局域性分布的灾难性测光红移[11](下文将用UL和BR分别指代左上角和右下角出现的灾难性测光红移)。为构造在z-zph面的左上角和右下角分别出现局域性分布的灾难性测光红移,令在前5个区间和最后10个区间才存在灾难性测光红移,而第5到第19个区间没有灾难性测光红移,见图 1。前5个区间的参数基准值统一为zcat,i=2.5,σcat,i=0.5(i=0到4),最后10个区间的参数基准值统一为zcat,i=0.4,σcat,i=0.3(i=20到29)。对所有存在灾难性测光红移的区间fi取相同值,并根据给定的灾难性测光红移的总比值Ft确定fi。用Ni表示测光红移分布归一化为1时任一测光红移区间的星系数目,$\sum\limits_{i \to {\rm{cat}}} {{N_i}} $表示包含灾难性测光红移的区间的星系数目总和,则fi和Ft的关系满足Ft=fi$\sum\limits_{i \to {\rm{cat}}} {{N_i}} $。本文采用(13)式作为星系的测光红移分布,经计算fi和Ft的关系满足fi=3.65Ft。描述灾难性测光红移的参数共有15 × 3=45个。
|
| 图 1 灾难性测光红移误差分布示意图。测光红移从0到3分成30个区间,灾难性测光红移分布在右下角(分布在前5个区间)和左上角(分布在最后10个区间)。矩形的半宽表示灾难性测光红移分布的标准差 Fig. 1 Schematic diagram of the catastrophic photo-z error distribution. The Photo-z space is divided into 30 bins from 0 to 3. The catastrophic photo-z is distributed at the bottom-right (0th-4th bin) and the upper-left (20th-29th bin) of the z-zph plane |
参照文[19]的方法,在真实红移为0到3分成30个区间,每个节点对应一个星系偏袒因子参数,共31个,其他红移上的偏袒因子通过线性插值得到。星系偏袒因子的基准值随真实红移的变化关系为b=1+0.84z[26]。
假设每个重子声波振荡区间用ntr个光谱红移校正。测光红移模型中参数的先验误差与ntr的关系为[13]
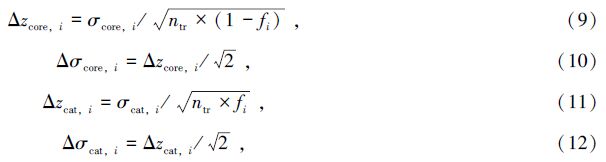
宇宙学参数取10个,它们分别是暗能量状态方程参数w0和wa,重子密度ωb,暗物质密度ωc,曲率的等价成分比Ωk,约化的哈勃常数h,原初氦丰度Yp,谱指数ns,谱指数的移动(running)α(定义同[19]),原初曲率功率谱在k=0.05Mpc-1处的幅值ΔR2。w0和wa是描述随红移演化的暗能量状态方程:w=w0+wa1-a。这些参数基准值和先验误差主要参考了PLANK2013年的结果[27],具体见表 1。
| w0 | wa | ωb | ωc | Ωk | h | Yp | ns | α | Δ2R | |
| 基准值 | -1 | 0 | 0.022 | 0.12 | 0 | 0.673 | 0.248 | 0.96 | -0.013 | 2.196E-9 |
| 先验误差 | 0.5 | 2.5 | 2.8E-4 | 2.7E-3 | 0.023 | 0.012 | 1.2E-4 | 7.3E-3 | 9.0E-3 | 5.6E-11 |
本文依据大口径全天巡视望远镜的巡天能力设定巡天参数。取星系的测光红移分布为

参照[28],本文取

用Nb和Nw分别表示重子声波振荡区间的数目和弱引力透镜区间的数目,用Nbw表示它们的数目之和,即Nbw=Nb+Nw=36。
参数{pα}的费舍尔矩阵可表示为[29]
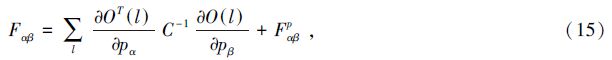
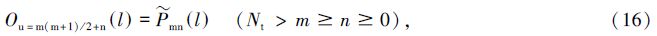
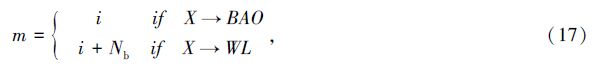
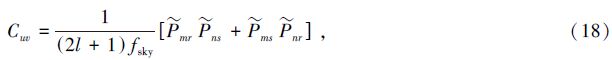
参数的协方差矩阵与相应的费舍尔矩阵互逆。本文计算的任一参数的限制误差都是把其他参数边缘化后的误差,即σpα=[F-1]αα。
假设观测量存在系统误差,则拟合的参数会出现偏离,可以用费舍尔矩阵估计系统误差给参数带来的偏差{δpα}[10, 13, 30]:
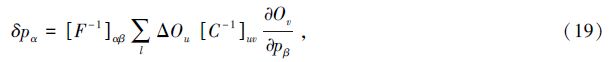
为避免可能存在的暗能量成团性效应,本文忽略大尺度的星系及其图像切变统计信息[28],同时为避免小尺度非线性效应和重子效应[15, 31],对于弱引力透镜取40<l<2000,对于重子声波振荡取40<l<3000。且重子声波振荡还要求功率谱Δδ2(k;z)<0.4,在实际处理时z取相应重子声波振荡区间的中心值。
2.1 由灾难性测光红移导致的暗能量状态方程参数的系统偏差表 2是没有灾难性测光红移误差时对暗能量状态方程参数的限制情况以及由Ft=0.02的灾难性测光红移误差导致的暗能量状态方程参数的偏差。其中,σ(p)是没有灾难性测光红移误差时的限制情况;δp是灾难性测光红移导致的偏差;δp/σ(p)即两者比值。δp和δp/σ(p)下分别有3列,分别对应于图 1中左上角出现的灾难性测光红移,右下角出现的灾难性测光红移和左上角+右下角出现的灾难性测光红移的情况。注意Ft是指包括左上角出现的灾难性测光红移和右下角出现的灾难性测光红移在内的总比值,当只有左上角出现的灾难性测光红移或右下角出现的灾难性测光红移误差时,相应的fi仍然满足fi=3.65Ft。
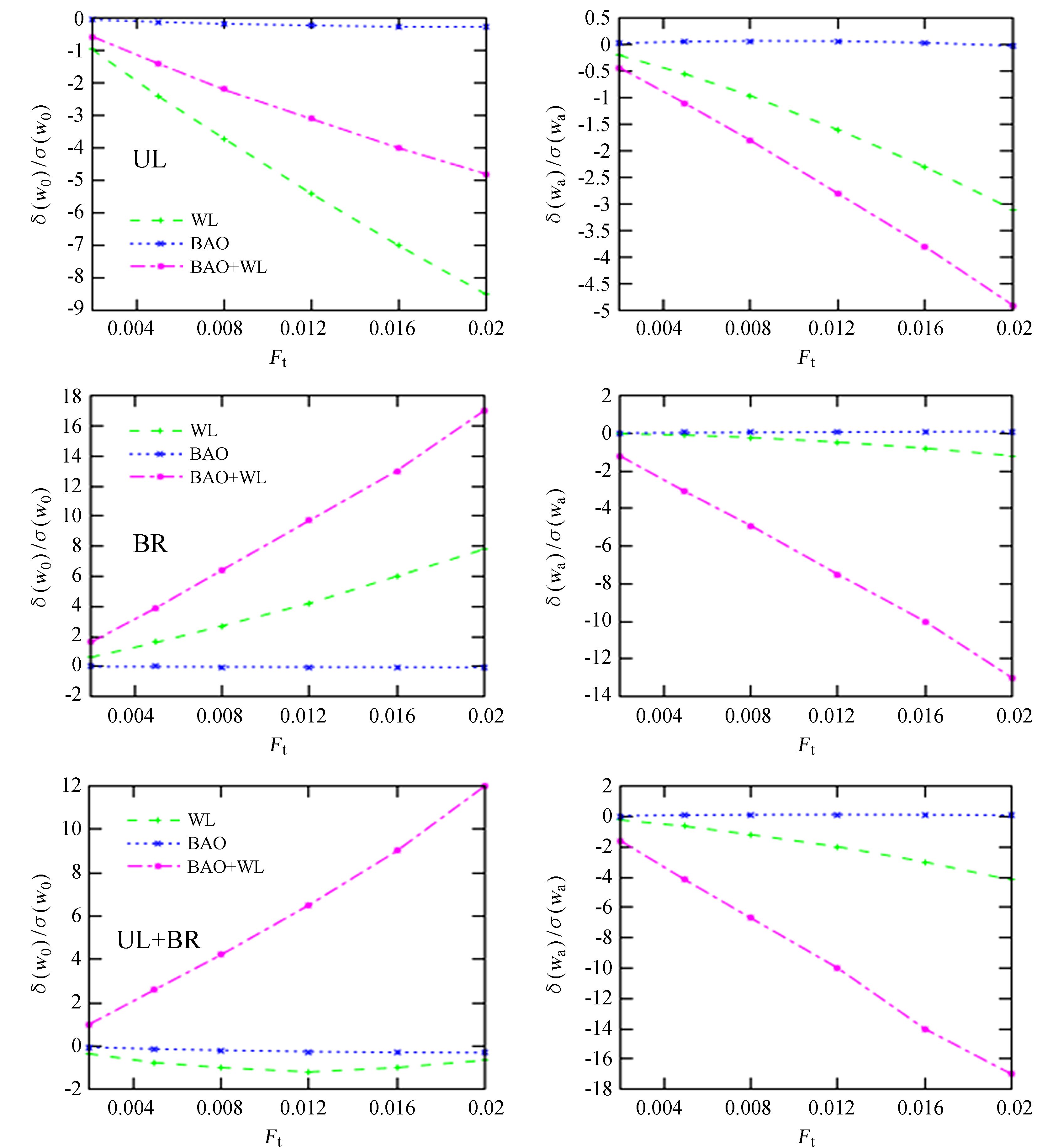
从表 2和图 2可以看出,左上角出现的灾难性测光红移和右下角出现的灾难性测光红移的影响有些是正负反号的(重子声波振荡对wa,弱引力透镜对w0,重子声波振荡+弱引力透镜对w0),特别在弱引力透镜限制w0的影响上,左上角出现的灾难性测光红移和右下角出现的灾难性测光红移造成的偏差大小几乎相等,但符号却相反,从而导致总体的影响反而变得很小。重子声波振荡受灾难性测光红移误差的影响最小(见表 2和图 2),对于Ft=0.02,最大的影响是左上角和右下角出现的灾难性测光红移两部分对w0的偏差(相对偏差为31%,见表 2)。
| σ(p) | δp | δp/σ(p) | ||||||
| ULa | BRb | BOTHc | UL | BR | BOTH | |||
| BAO | w0 wa | 0.1188 0.4191 | -0.031 -0.0097 | -0.0058 +0.04 | -0.037 +0.030 | -0.26 -0.023 | -0.049 +0.095 | -0.31 +0.072 |
| WL | w0 wa | 0.088 0.340 | -0.75 -1.1 | +0.69 -0.42 | -0.058 -1.4 | -8.5 -3.1 | +7.8 -1.2 | -0.66 -4.2 |
| BAO+WL | w0 wa | 0.064 0.2081 | -0.31 -1.0 | +1.1 -2.7 | +0.75 -3.6 | -4.8 -4.9 | +17 -13 | +12 -17 |
| a) include UL only; b) include BR only; c)include UL+BR | ||||||||
|
| 图 2 δ(w0)/σ(w0 )以及δ(wa)/σ(wa )随Ft的变化。左边3幅图从上到下分别是图 1中左上角、右下角以及这两部分灾难性测光红移误差对w0造成的相对偏差。右边3幅图同左,但是对wa造成的相对偏差 Fig. 2 The variations of δ(w0)/σ(w0 ) and δ(wa)/σ(wa ) with Ft. The three panels on the left are the impact of the upper-left (UL),bottom-right (BR) and both the two parts (UL+BR) catastrophic photo-z in Fig. 1 on w0. The right panels are the same as the left but for impact on wa |
灾难性测光红移误差对重子声波振荡的影响相对弱引力透镜较小的原因是由于弱引力透镜的窗函数比重子声波振荡的要宽得多,尤其对于红移较远的区间更甚。因此弱引力透镜窗函数比重子声波振荡受灾难性测光红移误差的影响更明显,从而直接导致弱引力透镜的功率谱比重子声波振荡受灾难性测光红移误差的影响更明显。
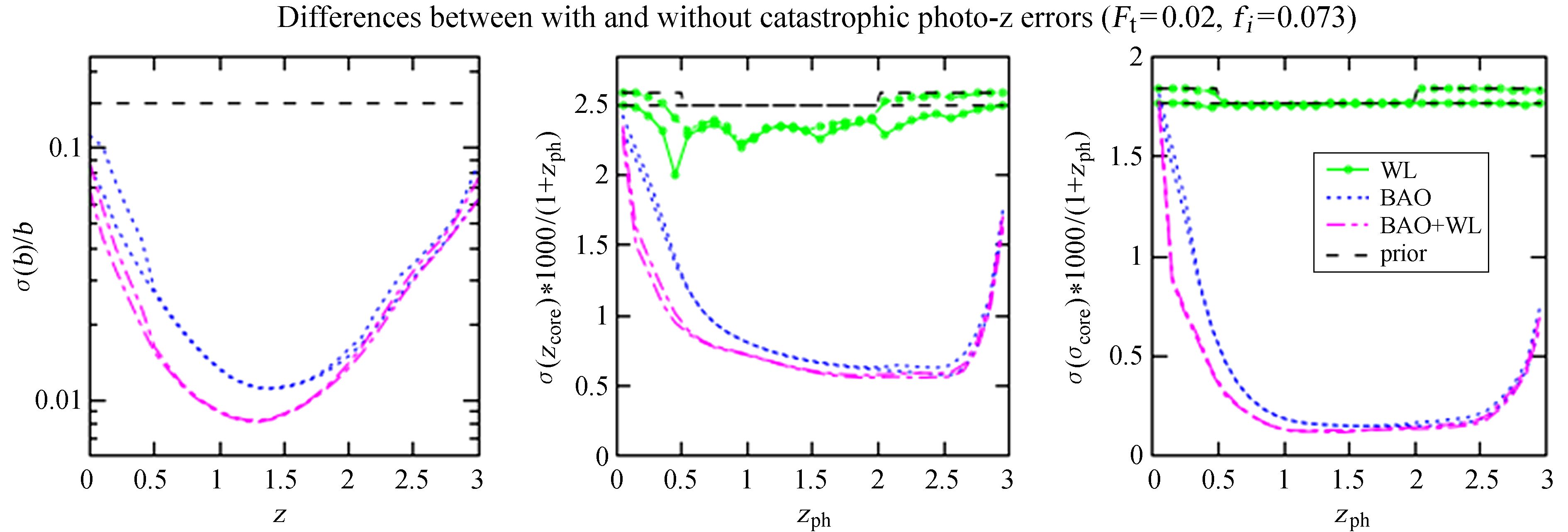
2.2 把灾难性测光红移的误差分布加入拟合模型中时暗能量状态方程参数的限制情况在没有灾难性测光红移误差的情况下,由于弱引力透镜不受星系偏袒因子的影响,联合重子声波振荡可以有效地提高对星系偏袒因子的限制能力[19]。让测光红移误差模型包括灾难性测光红移误差,结果发现,对于Ft=0.02,在测光红移误差模型添加了15 × 3=45个自由度后,星系偏袒因子b,测光红移区间的核心部分的星系真实红移分布的平均值zcore,i和标准差σcore,i的限制情况与没有灾难性测光红移误差的情况并没有实质性的差别。图 3比较这种情况下与没有灾难性测光红移误差时b、zcore,i和σcore,i的限制情况。重子声波振荡和联合重子声波振荡+弱引力透镜对b的限制受灾难性测光红移误差的影响主要出现在相应区间附近(即z<0.5和z>2),而中间没有灾难性测光红移误差的区域则不受影响。总体来说,联合重子声波振荡和弱引力透镜仍然使星系偏袒因子得到比单独重子声波振荡更强的限制。另外,重子声波振荡和联合重子声波振荡+弱引力透镜对zcore,i和σcore,i的限制几乎没有变化。综上所述,在加入Ft=0.02的灾难性测光红移误差的情况下,重子声波振荡和弱引力透镜仍然具有很强的互补效应。
|
| 图 3 比较存在和不存在局域性灾难性测光红移的两种模型下重子声波振荡,弱引力透镜及联合重子声波振荡+弱引力透镜的校正能力。3张子图的图例相同并画在第3张子图上。第1张子图是重子声波振荡和联合重子声波振荡+弱引力透镜对星系偏袒因子的限制情况,并分别对应两条曲线,略高者为存在灾难性测光红移的情况(后面两子图同理)。每个参数的先验误差为15%。第2张子图是弱引力透镜、重子声波振荡和联合重子声波振荡+弱引力透镜对zcore,i的限制情况。先验误差为Δzcore,i=0.05σcore,i/$\sqrt {1 - {f_i}} $。第3张子图是对σcore,i的限制情况。先验误差是Δzcore,i的1/$\sqrt 2 $倍,对重子声波振荡和联合重子声波振荡+弱引力透镜,图中几乎分辨不出存在和不存在灾难性测光红移的限制差别。子图 2,3中弱引力透镜的限制情况在0<zph<0.5和2<zph<3出现明显的差别是由于先验误差的取值不同造成的 Fig. 3 The comparison of different constrains by BAO,WL and BAO+WL between with and without localized catastrophic photo-z error (Ft=0.02). The legends for each panel are the same and put in the 3rd panel. The 1st panel is constrains of galaxy biases by BAO and BAO+WL and each has two curves respectively corresponding to the one with and without catastrophic photo-z error respectively. For both BAO and BAO+WL,the curve which is a little higher is the one with catastrophic photo-z error (The same for the 2nd and 3rd panel). The prior for each galaxy bias parameter is 15%. The 2nd panel is constrains of zcore,i by BAO,WL,BAO+WL. The prior is Δzcore,i=0.05σcore,i/$\sqrt {1 - {f_i}} $. The 3rd panel is constrains of σcore,i. The prior for σcore,i is Δzcore,i/$\sqrt 2 $. For BAO and BAO+WL constrains,the curves with and without catastrophic photo-z errors are almost the same in the 3rd panel. The obvious differences between WL constrains at 0<zph<0.5 and 2<zph<3 is due to the different priors adopted |
表 3列出了加入灾难性测光红移误差到测光红移误差分布模型中之后的暗能量状态方程参数的限制情况,并与没有灾难性测光红移误差时的结果做了比较。在加入Ft=0.02的灾难性测光红移误差后,总体来看,暗能量状态方程参数的误差并没有太大的增加。特别是重子声波振荡的限制结果增加量少于1%。弱引力透镜对w0和wa的限制误差分别增加了14%左右(UL+BR)和6%左右(UL+BR)。而联合重子声波振荡+弱引力透镜对w0和wa的限制误差都只增加了5%左右(UL+BR)。
3 总结及讨论本文建构了在z-zph面左上角和右下角局域性分布的灾难性测光红移误差分布模型。计算了由于不知道灾难性测光红移误差的存在(Ft=0.02)导致的重子声波振荡、弱引力透镜以及联合重子声波振荡+弱引力透镜限制暗能量状态方程参数时的系统偏差,并分别考察左上角和右下角部分的测光红移误差造成的影响。结果发现,左上角和右下角造成的偏差有些是正负反号的(重子声波振荡对wa,弱引力透镜对w0,联合重子声波振荡+弱引力透镜对w0),特别在对弱引力透镜限制w0的影响上,左上角和右下角造成的偏差大小几乎相等,但符号却相反,从而导致总体的影响反而变得很小。重子声波振荡受灾难性测光红移误差的影响最小,对于Ft=0.02,对重子声波振荡最大的影响是左上角+右下角两部分对w0造成的偏差(31%)。最后把Ft=0.02的灾难性测光红移误差加入测光红移误差模型中,计算增加45个自由度后对星系偏袒因子、测光红移误差参数以及暗能量状态方程参数的限制。结果在加入Ft=0.02的灾难性测光红移误差的情况下,重子声波振荡和弱引力透镜仍然具有很强的互补效应。重子声波振荡和联合重子声波振荡+弱引力透镜对星系偏袒因子的限制受灾难性测光红移误差的影响主要出现在相应有灾难性测光红移误差的区间附近(即z<0.5和z>2),而中间没有灾难性测光红移误差的区域则几乎不受影响。总体来说,联合重子声波振荡和弱引力透镜仍然使星系偏袒因子得到比单独重子声波振荡更强的限制。另外,重子声波振荡和联合重子声波振荡+弱引力透镜对zcore,i和σcore,i的限制几乎没有变化。至于对暗能量状态方程参数限制的影响,在把Ft=0.02的灾难性测光红移误差加入拟合模型后,暗能量状态方程参数的误差并没有太大的增加。特别是重子声波振荡的限制结果增加量少于1%。弱引力透镜对w0和wa的限制误差分别增加了14%左右(UL+BR)和6%左右(UL+BR),而联合重子声波振荡+弱引力透镜对w0和wa的限制误差都只增加了5%左右(UL+BR)。
| add cata | Rb(10-2) | ||||||
| UL | BR | BOTH | UL | BR | BOTH | ||
| BAO | w0 wa | 0.11960 0.4217 | 0.1189 0.4193 | 0.11963 0.4218 | 0.67 0.62 | 0.08 0.05 | 0.70 0.64 |
| WL | w0 wa | 0.097 0.355 | 0.095 0.345 | 0.10 0.360 | 10 4.4 | 8.0 1.5 | 14 5.9 |
| BAO+WL | w0 wa | 0.065 0.2120 | 0.066 0.2119 | 0.067 0.2159 | 1.6 1.9 | 3.1 1.8 | 4.7 5.5 |
a.“cat” means “catastrophic photo-z error”;b. R=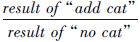 -1 -1
| |||||||
致谢:感谢国家天文台詹虎研究员在研究过程中给予的宝贵意见和指导。感谢孙磊、许优华、王乔在此过程中非常有益的讨论和帮助。
| [1] | Connolly A J,Csabai I,Szalay A S,et al.Slicing through multicolor space:galaxy redshifts from broadband photometry[J].The Astronomical Journal,1995,110(6):2655-2664. |
| [2] | Carliles S,Budavári T,Heinis S,et al.Random forests for photometric redshifts[J].The Astrophysical Journal,2010,712:511-515. |
| [3] | Bolzonella M,Miralles J M,Pello R,et al.Photometric redshifts based on standard SED fitting procedures[J].Astronomy & Astrophysics,2000,363:476-492. |
| [4] | Collisster A A,Lahav O.ANNz:estimating photometric redshifts using artificial neural networks[J].The Publications of the Astronomical Society of the Pacific,2004,116(818):345-351. |
| [5] | Schneider M K L,Zhan H C A.Using galaxy two-point correlation functions to determine the redshift Distributions of galaxies binned by photometric redshift[J].The Astrophysical Journal,2006,651(1):14-23. |
| [6] | Newman J A.Calibrating redshift distributions beyond spectroscopic limits with cross-correlations[J].The Astrophysical Journal,2008,684(1):88-101. |
| [7] | Benjamin J,Waerbeke L V,Ménard B,et al.Photometric redshifts:estimating their contamination and distribution using clustering information[J].Monthly Notices of the Royal Astronomical Society,2010,408:1168-1180. |
| [8] | Schmidt S J,Ménard B,Scranton R.Recovering redshift distributions with cross-correlations:pushing the boundaries[J].Monthly Notices of the Royal Astronomical Society,2013,431(4):3307-3318. |
| [9] | Ma Z,Hu W,Huterer D.Effects of photometric redshift uncertainties on weak-lensing tomography[J].The Astrophysical Journal,2006,636(1):21-29. |
| [10] | Huterer D,Takada M,Bernstein G,et al.Systematic errors in future weak lensing surveys:requirements and prospects for self-calibration[J].Monthly Notices of the Royal Astronomical Society,2006,366(1):101-114. |
| [11] | Sun L,Fan Z H,Tao C,et al.Catastrophic photo-z errors and the dark energy parameter estimates with cosmic shear[J].The Astrophysical Journal,2009,699:958-967. |
| [12] | Bernstein G,Huterer D.Catastrophic photometric redshift errors:weak-lensing survey requirements[J].Monthly Notices of the Royal Astronomical Society,2010,401(2):1399-1408. |
| [13] | Hearin A P,Zentner A R,Ma Z,et al.A general study of the influence of catastrophic photometric redshift errors on cosmology with cosmic shear tomography[J].Astrophysical Journal,2010,720(2):1351-1369. |
| [14] | Nishizawa A J,Takada M,Hamana T,et al.A clipping method to mitigate the impact of catastrophic photometric redshift errors on weak lensing tomography[J].The Astrophysical Journal,2010,718(2):1252-1265. |
| [15] | Seo H J,Eisenstein D J.Probing dark energy with baryonic acoustic oscillations from future large galaxy redshift surveys[J].The Astrophysical Journal,2003,598(2):720-740. |
| [16] | Zhan H,Knox L,Tyson J A.Distance,growth factor,and dark energy constraints from photometric baryon acoustic oscillation and weak lensing measurements[J].The Astrophysical Journal,2009,690(1):923-936. |
| [17] | Knox L,Song Y S,Zhan H.Weighing the universe with photometric redshift surveys and the impact on dark energy forecasts[J].The Astrophysical Journal,2006,652(2):857-863. |
| [18] | Zhan H,Knox L.Baryon oscillations and consistency tests for photometrically determined redshifts of very faint galaxies[J].The Astrophysical Journal,2006,644(2):663-670. |
| [19] | Zhan H.Cosmic tomographies:baryon acoustic oscillations and weak lensing[J].Journal of Cosmology and Astroparticle Physics,2006,4(8):747-748. |
| [20] | Limber D N.The analysis of counts of the extragalactic nebulae in terms of a fluctuating density field.Ⅱ[J].The Astrophysical Journal,1954,119:655-681. |
| [21] | Kaiser N.Weak gravitational lensing of distant galaxies[J].The Astrophysical Journal,1992,388:272-286. |
| [22] | Lewis A,Challinor A,Lasenby A.Efficient computation of cosmic microwave background anisotropies in closed friedmann-robertson-walker models[J].The Astrophysical Journal,2000,538(2):473-476. |
| [23] | Howlett C,Lewis A,Hall A,et al.CMB power spectrum parameter degeneracies in the era of precision cosmology[J].Journal of Cosmology and Astroparticle Physics,2012,4(4):1-27. |
| [24] | Smith R E,Peacock J A,Jenkins A,et al.Stable clustering,the halo model and non-linear cosmological power spectra[J].Monthly Notices of the Royal Astronomical Society,2003,341(4):1311-1332. |
| [25] | Takahashi R,Sato M,Nishimichi T,et al.Revising the halofit model for the nonlinear matter power spectrum[J].The Astrophysical Journal,2012,761(2):152-161. |
| [26] | Weinberg D H,Dave' R,Katz N,et al.Galaxy clustering and galaxy bias in a ΛCDM universe[J].The Astrophysical Journal,2004,601(1):1-21. |
| [27] | Plank Collaboration,Ade P A R,Aghanim N,et al.Planck 2013 results.XVI.cosmological parameters[J].Astronomy and Astrophysics,2014,571:A16-A81. |
| [28] | Song Y S,Knox L.Determination of cosmological parameters from cosmic shear data[J].Physical Review D,2004,70(6):298. |
| [29] | Tegmark M.Measuring cosmological parameters with galaxy surveys[J].Physical Review Letters,1997,79(20):3806-3809. |
| [30] | Amara A,Réfrégier A.Systematic bias in cosmic shear:extending the Fisher matrix[J].Monthly Notices of the Royal Astronomical Society,2008,391(1):228-236. |
| [31] | Seo H J,Eisenstein D J.Baryonic acoustic oscillations in simulated galaxy redshift surveys[J].The Astrophysical Journal,2005,633(2):575-588. |


