Blazar黑洞自旋能量与红移相关性研究

引用本文

张旭, 张雄. Blazar黑洞自旋能量与红移相关性研究[J]. 天文研究与技术, 2015, 12(3): 253-261 复制到剪切板

Zhang Xu, Zhang Xiong. A Study of Correlations between Redshifts and Spin Energies of Black Holes in AGN[J]. ASTRONOMICAL RESEARCH & TECHNOLOGY, 2015, 12(3): 253-261. 复制到剪切板

Blazar黑洞自旋能量与红移相关性研究

张旭, 张雄

云南师范大学物理与电子信息学院, 云南昆明 650500

收稿日期: 2014-10-12

基金项目: 国家自然科学基金(U1231203);国家自然科学基金(11163007);云南省自然科学基金项目(2010CD046);云南省高能天体物理重点实验室资助.

作者简介: 张旭,男,硕士.研究方向:黑洞,活动星系核.Email:2226997466@qq.com

通讯作者: 张雄,男,教授.研究方向:黑洞,活动星系核.Email:kmzhanghj@163.com

摘要: 黑洞自旋及其参量能提供黑洞合并及吸积的信息。从文献资料中收集了112个Blazar源,这些源包含了67个FR II射电星系(RG),11个FR II射电噪类星体(RLQ),27个核占优星系(CD)。通过样本数据研究黑洞自旋能量与红移的相关性。研究结果表明:(1)112个Blazar的黑洞自旋能量与红移存在相关性,尤其在爱丁顿磁场条件下(B=B_EDD),黑洞自旋能量与红移的相关性最为明显;(2)FR II射电星系(RG)、FR II射电噪类星体(RLQ)、核占优星系(CD)的黑洞自旋能量在3种磁场条件下(B=B_EDD,B=10⁴G,B∝j)与红移的相关性强弱上存在差异,但总体趋势较为相似,均呈现正比关系;(3)黑洞自旋能量与红移的强相关性表明,黑洞自旋能量在一定程度上给出黑洞并合与吸积的信息。这些研究结果与其他人用其他方法获得的结果是一致的。

关键词： Blazar 黑洞自旋自旋能量红移相关性

A Study of Correlations between Redshifts and Spin Energies of Black Holes in AGN

Zhang Xu, Zhang Xiong

College of Physics and Electronic Information Technology, Yunnan Normal University, Kunming 650500, China

Abstract: We have collected a sample of 112 Blazars. Our sample includes 67 FRII Quasars, 11 FRII Radio-Loud Quasars, and 27 FRII cD galaxies. The Quasars and Radio-Loud Quasars have redshifts from about 0 to about 2. We have analyzed correlations between redshifts and spin energies of black holes for our sampled AGN. The spin energies were calculated using a set of assumptions. Our conclusions are as follows. (1) The spin energies of the sampled Blazars show appreciable correlations with redshifts; the correlations are most obvious if magnetic-field strengths (B)around the black holes are assumed to follow B=B_EDD; (2) The correlations are similar for different types of Blazars and for three different assumptions of magnetic-field strengths (, i.e., B=B_EDD, B=10⁴G, and B∝j_M); (3) The results suggest that spin energies statistically increase with redshifts for black holes in the redshift range of 0 to 3, which is consistent with independent studies of other authors.

Blazar Spin of a black hole Spin energy Redshfit Correlation

黑洞自旋和质量是Blazar的两个基本物理量。黑洞自旋与黑洞合并和吸积有着明显的关系^[1]。文^{[2, 3, 4, 5, 6, 7]}的研究均得出相同的结论。文^[2]认为黑洞自旋和质量的变化在二元合并时是同时发生的。在并合的过程中黑洞的自旋速率会慢慢降低。文^[6]认为大质量黑洞的吸积可能是由一系列连续随机的吸积事件组成的，正是由于这些吸积事件使大质量黑洞具有中等的自旋。文^[8]认为自旋及其参量与红移一样的功能，能对AGN黑洞的并合与吸积特征进行精确的描绘。

大质量黑洞自旋的研究为大质量黑洞合并与吸积提供了全新的视角。现在有很多可行的方法估算大质量黑洞的自旋。例如当AGN吸积盘区域能观测到X射线时，就可根据其辐射光谱的特性估算黑洞自旋^[9]。又如当一个AGN拥有较强的喷流时，其喷流的特性也可用于估算AGN黑洞的自旋大小。正如文^[10]所总结的，当黑洞样本中有X射线辐射源或较强的喷流时能提供一个凭借经验估算黑洞自旋的途径。

在文^{[11, 12]}的模型中黑洞自旋能量与自旋在不同磁场下均存在紧密的联系。研究显示，黑洞自旋能量作为黑洞自旋的重要参量，与红移之间同样存在着相关性。文^[5]认为，对自旋及其自旋能量的研究同红移一样，可以对AGN黑洞的合并吸积特性进行精确的描绘。但目前为止自旋及自旋能量与红移关系仍没有统一定论。

文^[1]讨论了自旋与红移的关系，其结果表明自旋与红移存在着明显的相关性。但对于黑洞自旋能量仅仅讨论了黑洞吸积盘提取的自旋能量片段，没有详细讨论黑洞自旋与黑洞质量共同作用下的总自旋能量与红移的相关性。本文对黑洞的自旋能量与红移进行相关性分析。

运用文^{[1, 13]}的黑洞样本数据为基础将数据扩大到112个Blazer源，其中包含了67个FR II射电星系(RG)、11个FR II射电噪类星体(RLQ)、27个中核星系(CD)。运用黑洞自旋的关系式计算出自旋能量，讨论了不同类型的源在3种不同特性磁场下黑洞自旋能量与红移的相关特性，得出的结果表明Blazer黑洞自旋能量与红移存在较为直接的联系，这与文^[1]得出的结论相同。同时也表明黑洞自旋能量同样能在一定程度上给出黑洞合并与吸积的信息。本文给出了用模型公式估算Blazer自旋能量大小的方法，为下一步自旋能量与模型的研究提供了依据。

1 黑洞自旋及自旋能量的计算 1.1 黑洞自旋

计算黑洞自旋数据的方法与文^[13]相同。在著名的BZ模型中电子束功率L_j的产生与自旋j的关系：

L_j=(j²B²_p0r²Hc)/32≈2×10⁴³ j²M²₈B²₄erg s^-1 ，

(1)

r_H为黑洞视界半径(r_H=2GM/c²)；B_p0为黑洞视界磁场强度；j≡Sc/(GM²)；M₈为10⁸M_⊙为单位的黑洞质量；B₄为10⁴G为单位的电磁场轴相分量强度。

jb_BZ≈(B_E,4M₈)^-15L₄₄≈17.5L_j/LE

(2)

b_BZ≡B_p0/B_E为黑洞磁场强度；B_E,4≈6M^-1/2₈为爱丁顿磁场；L_E≈1.26×10⁴⁶M₈ erg s^-1 为黑洞爱丁顿光度。由L_j=k L_j(BZ)、jb=jb_BZ/k及k [jb_BZ]²可得出如下关系式：

L_j(M)≈10⁴⁴j²M²₈B²₄ erg s^-1 .

(3)

当黑洞喷流较强时用这种方法估算黑洞自旋比较准确^[13]。这种方法是基于喷流较强时其自旋能量与旋转的黑洞周围区域的吸积物质有关的标准模型^{[14, 15, 16]}。很多黑洞自旋与喷流电子束关系模型中http://arxiv.org/abs/1307.3246，磁场强度和黑洞质量通常被设定为常数^{[17, 18]}，它们有如下关系^{[19, 20]}：

L_j∝j²M²B² ，

(4)

L_j为黑洞喷流电束功率；M是黑洞质量；j为黑洞自旋量，j=a/m ，a=S/(Mc)，m=GM/c²；S为黑洞自旋的角动量大小；c为光速；B为吸积盘和黑洞的电磁场轴相分量的强度^[21]。由此算出黑洞自旋量j的值http://arxiv.org/abs/1312.6698：

j=k(L₄₄)^0.5B₄^-1M₈^-1 ，

(5)

L₄₄是以10⁴⁴ erg/s为单位的喷流电子束功率；B₄是以10⁴G为单位的电磁场轴向量强度；M₈以10⁸M_⊙为单位的黑洞质量。比例常数k的数值根据不同的模型而变化，例如在文^[10]的模型中k≈(1.05)^-1/2，在文^[11]的模型中k≈5。在对恒星质量黑洞的研究中，应用(4)式能很好地描述黑洞自旋与喷流电子束功率之间的关系^[22]，Narayan & McClintock独立研究估算出的5个恒星质量的黑洞自旋与喷流电子束功率所呈现的比列关系与(4)式所描述的相符合。数据结果是应用文^[10]的模型的计算结果，也可应用其他模型计算。

1.2 自旋能量

在本文中运用文^[1]的计算公式求出黑洞样本的自旋能量。用(5)计算出黑洞自旋j后，可以用其估算自旋能量E_S^[23]：

ESMc²=1-(1+[1-j²]^1/22)^1/2 .

(6)

得到的E_SMc²要比其他数据小很多，因为r≡E_S(Mc²)是对自旋j的详细描绘，r总体来说是很小的。(6)式可以很好地描绘自旋j和自旋能量的关系。通过(6)式可以得到E_SMc²的值，通过黑洞质量M的数据算出自旋能量E_S的值。文^{[12, 13]}的模型中在不同磁场下的自旋能量都与自旋大小有着紧密联系。在对黑洞自旋能量进行估算时，也考虑了3种不同的磁场条件。即考虑了爱丁顿磁场、静磁场和与自旋有关的磁场，这3种磁场分别与黑洞的参数有联系。爱丁顿极限下的磁场定义为爱丁顿磁场，爱丁顿磁场以10⁴G为单位，B_EDD≌6M₈^-1/2^[24]，这种磁场是基于爱丁顿光度的辐射源所检测出的http://arxiv.org/abs/0810.1055，文^[21]认为很多AGN的辐射均在此光度下。为了比较爱丁顿磁场特性的影响，引入静磁场，其磁场强度以10⁴G为单位，B₄=1^{[23, 24, 25]}。作为对比研究引入了自旋磁场，如果黑洞的自旋能量是连续的，FRII射电星系的磁场强度与自旋成比例关系以10⁴G为单位，B₄≌2.78j^{[24, 26, 27]}。在文^[10]的模型及文^{[27, 28]}的经验推论中均表明磁场强度与自旋存在着某种联系(B∝j)，与自旋有关的磁场做为参考项对自旋能量与红移的关系研究非常有用。

2 实验结果

根据文^[1]及文^[15]的黑洞样本^{[1, 15]}收集扩充了Blazar源^[14]，用(5)、 (6)式计算了相关的量给出了表 1。本文着重讨论黑洞自旋能量与红移的相关性。计算过程这里不再复述。数据源按红移值由小到大排列。

表 1 黑洞红移质量自旋及自旋能量 Table 1 Data of redshift,mass,spin,and spin energy of our studied black holes

Source (1)	Type (2)	z (3)	L₄₄^a (4)	M₈^b (5)	J_M (B=B_EDD) (6)	E_s(B=B_EDD) Mc² (7)	J_M (B=10⁴) (8)	E_s(B=10⁴) Mc² (9)	J_M (B∝j) (10)	E_s(B∝j) Mc² (11)
3C405	RG	0.056	47	25	0.23	0.006 725	0.27	0.009 328	0.31	0.012 393
3C244.1	RG	0.43	14	9.5	0.2	0.005 064	0.38	0.018 933	0.37	0.017 902
3C172	RG	0.519	31	7.8	0.33	0.014 104	0.7	0.074 218	0.5	0.034 074
3C330	RG	0.549	80	13	0.41	0.022 226	0.68	0.069 083	0.49	0.032 601
3C427.1	RG	0.572	31	14	0.25	0.007 97	0.38	0.018 933	0.37	0.017 902
3C33	RG	0.059 5	2.4	3.7	0.13	0.002 124	0.42	0.023 393	0.39	0.019 996
3C192	RG	0.059 8	1.1	2.6	0.11	0.001 518	0.4	0.021 094	0.38	0.018 933
3C337	RG	0.63	20	9.1	0.25	0.007 97	0.48	0.031 169	0.41	0.022 226
3C35	RG	0.067 7	0.77	4.4	0.068	0.000 579	0.19	0.004 564	0.26	0.008 635
3C34	RG	0.69	65	16	0.33	0.014 104	0.48	0.031 169	0.41	0.022 226
3C441	RG	0.707	65	18	0.32	0.013 233	0.45	0.027 11	0.4	0.021 094
3C55	RG	0.72	180	14	0.58	0.047 473	0.91	0.158 986	0.57	0.045 63
3C247	RG	0.749	35	26	0.19	0.004 564	0.22	0.006 144	0.28	0.010 051
3C285	RG	0.079 4	1.1	3.4	0.093	0.001 084	0.3	0.011 582	0.33	0.014 104
3C452	RG	0.081 1	4.2	5.1	0.15	0.002 833	0.39	0.019 996	0.37	0.017 902
3C326	RG	0.089 8	2.2	2.4	0.16	0.003 226	0.6	0.051 317	0.46	0.028 424
3C388	RG	0.090 8	2.6	6.9	0.1	0.001 254	0.23	0.006 725	0.29	0.010 802
3C321	RG	0.096	1.7	6.1	0.086	0.000 927	0.21	0.005 59	0.27	0.009 328
3C289	RG	0.967	85	27	0.3	0.011 582	0.34	0.015 006	0.35	0.015 94
3C280	RG	0.996	53	27	0.23	0.006 725	0.26	0.008 635	0.31	0.012 393
3C236	RG	0.098 9	1.9	6.5	0.088	0.000 97	0.21	0.005 59	0.27	0.009 328
3C433	RG	0.101 6	6.3	9.2	0.14	0.002 465	0.27	0.009 328	0.31	0.012 393
3C223	RG	0.136 8	3.5	3	0.18	0.004 092	0.61	0.053 321	0.47	0.029 777
4C12.03	RG	0.156	3.3	7.1	0.11	0.001 518	0.25	0.007 97	0.3	0.011 582
3C28	RG	0.195 2	7.6	7.5	0.16	0.003 226	0.36	0.016 905	0.36	0.016 905
3C349	RG	0.205	6.7	3.6	0.22	0.006 144	0.7	0.074 218	0.5	0.034 074
3C132	RG	0.214	7.3	5.5	0.19	0.004 564	0.48	0.031 169	0.42	0.023 393
3C436	RG	0.214 5	9.4	7.1	0.19	0.004 564	0.42	0.023 393	0.39	0.019 996
3C171	RG	0.238 4	12	3.9	0.29	0.010 802	0.87	0.135 983	0.56	0.043 838
3C284	RG	0.239 4	8	7.8	0.17	0.003 646	0.36	0.016 905	0.36	0.016 905
3C79	RG	0.255 9	21	6	0.3	0.011 582	0.73	0.082 545	0.51	0.035 59
3C300	RG	0.272	14	3.6	0.33	0.014 104	1	0.292 893	0.61	0.053 321
3C153	RG	0.276 9	13	8.6	0.2	0.005 064	0.4	0.021 094	0.38	0.018 933
3C438	RG	0.29	36	13	0.27	0.009 328	0.45	0.027 11	0.4	0.021 094
3C14.27	RG	0.392	20	5.4	0.31	0.012 393	0.82	0.113 331	0.54	0.040 4
3C42	RG	0.395	21	8.8	0.25	0.007 97	0.51	0.035 59	0.43	0.024 595
3C16	RG	0.405	22	4.6	0.35	0.015 94	1	0.292 893	0.6	0.051 317
3C274.1	RG	0.422	32	8.6	0.31	0.012 393	0.64	0.059 688	0.48	0.031 169
3C457	RG	0.428	28	6.4	0.34	0.015 006	0.81	0.109 374	0.54	0.040 4
3C46	RG	0.437 3	25	15	0.21	0.005 59	0.31	0.012 393	0.34	0.015 006
3C341	RG	0.448	25	10	0.25	0.007 97	0.47	0.029 777	0.41	0.022 226
3C200	RG	0.458	27	8.8	0.29	0.010 802	0.58	0.047 473	0.46	0.028 424
3C295	RG	0.461 4	130	29	0.35	0.015 94	0.4	0.021 094	0.38	0.018 933
3C192	RG	0.482	29	14	0.23	0.006 725	0.37	0.017 902	0.36	0.016 905
3C225B	RG	0.58	76	10	0.45	0.027 11	0.85	0.126 277	0.55	0.042 095
3C49	RG	0.602 07	42	13	0.29	0.010 802	0.49	0.032 601	0.42	0.023 393
3C277.2	RG	0.766	85	11	0.45	0.027 11	0.83	0.117 457	0.54	0.040 4
3C340	RG	0.775 4	65	11	0.4	0.021 094	0.72	0.079 681	0.51	0.035 59
3C352	RG	0.806	83	16	0.37	0.017 902	0.57	0.045 63	0.45	0.027 11
3C263.1	RG	0.824	130	19	0.43	0.024 595	0.6	0.051 317	0.46	0.028 424
3C175.1	RG	0.92	110	12	0.49	0.032 601	0.85	0.126 277	0.55	0.042 095
3C356	RG	1.079	250	28	0.5	0.034 074	0.55	0.042 095	0.44	0.025 834
3C252	RG	1.105	170	20	0.47	0.029 777	0.63	0.057 505	0.48	0.031 169
3C368	RG	1.132	240	28	0.48	0.031 169	0.54	0.040 4	0.44	0.025 834
3C267	RG	1.144	190	24	0.47	0.029 777	0.55	0.042 095	0.44	0.025 834
3C324	RG	1.21	150	37	0.34	0.015 006	0.33	0.014 104	0.34	0.015 006
3C266	RG	1.272	220	23	0.5	0.034 074	0.62	0.055 383	0.47	0.029 777
3C13	RG	1.351	260	40	0.41	0.022 226	0.39	0.019 996	0.38	0.018 933
4C13.66	RG	1.45	260	16	0.66	0.064 247	0.99	0.244 663	0.6	0.051 317
3C68.2	RG	1.575	210	35	0.41	0.022 226	0.41	0.022 226	0.38	0.018 933
3C241	RG	1.617	370	37	0.51	0.035 59	0.5	0.034 074	0.43	0.024 595
3C470	RG	1.653	290	28	0.53	0.038 751	0.6	0.051 317	0.47	0.029 777
3C322	RG	1.681	510	32	0.66	0.064 247	0.68	0.069 083	0.49	0.032 601
3C294	RG	1.786	440	29	0.64	0.059 688	0.71	0.076 907	0.51	0.035 59
3C239	RG	1.79	480	37	0.6	0.051 317	0.58	0.047 473	0.45	0.027 11
3C334	RLQ	0.555	62	50	0.19	0.004 564	0.15	0.002 833	0.23	0.006 725
3C254	RLQ	0.734	63	20	0.3	0.011 582	0.39	0.019 996	0.37	0.017 902
3C175.1	RLQ	0.768	130	79	0.21	0.005 59	0.14	0.002 465	0.22	0.006 144
3C336	RLQ	0.927	100	16	0.41	0.045 63	0.63	0.211 614	0.47	0.049 368
3C245	RLQ	1.029	160	25	0.41	0.022 226	0.49	0.057 505	0.42	0.029 777
3C212	RLQ	1.049	190	16	0.56	0.022 226	0.84	0.032 601	0.55	0.023 393
3C186	RLQ	1.063	210	32	0.41	0.043 838	0.44	0.121 767	0.4	0.042 095
3C208	RLQ	1.109	230	25	0.49	0.022 226	0.59	0.025 834	0.46	0.021 094
3C204	RLQ	1.112	170	32	0.38	0.032 601	0.4	0.049 368	0.38	0.028 424
4C16.49	RLQ	1.296	220	63	0.3	0.018 933	0.23	0.021 094	0.29	0.018 933
3C68.1	RLQ	1.238	410	79	0.38	0.018 933	0.25	0.007 97	0.3	0.011 582
3C181	RLQ	1.382	330	40	0.47	0.011 582	0.44	0.006 725	0.4	0.010 802
3C268.4	RLQ	1.4	830	63	0.6	0.051 317	0.45	0.027 11	0.4	0.021 094
3C191	RLQ	1.952 3	600	50	0.56	0.029 78	0.48	0.027 11	0.41	0.021 094
3C9	RLQ	2.012	940	63	0.63	0.043 838	0.47	0.031 2	0.41	0.022 226
M87	CD	0.004 2	0.06	8.6	0.014	0.000 01	0.028	0.000 1	0.1	0.001 254
Centaurus	CD	0.011	0.074	8.6	0.015	0.000 03	0.031	0.000 1	0.1	0.001 254
HCG 62	CD	0.014	0.039	5.7	0.014	0.000 03	0.034	0.000 12	0.11	0.001 254
A262	CD	0.016	0.097	8.6	0.018	0.000 02	0.035	0.000 145	0.11	0.001 518
Perseus	CD	0.018	1.5	17	0.049	0.000 04	0.07	0.000 153	0.16	0.001 518
PKS1404 -267	CD	0.022	0.2	5.7	0.031	0.000 3	0.076	0.000 613	0.16	0.003 226
A2199	CD	0.03	2.7	20	0.061	0.000 12	0.08	0.000 723	0.17	0.003 226
A2052	CD	0.035	1.5	17	0.049	0.000 466	0.07	0.000 802	0.16	0.003 646
2A0335 +096	CD	0.035	0.24	14	0.022	0.000 3	0.033	0.000 613	0.11	0.003 226
MKW 3S	CD	0.045	4.1	8.6	0.12	0.000 05	0.23	0.000 136	0.29	0.001 518
A4059	CD	0.048	0.96	29	0.031	0.001 808	0.033	0.006 725	0.11	0.010 802
Hydra A	CD	0.055	4.3	11	0.1	0.000 12	0.18	0.000 136	0.25	0.001 518
A85	CD	0.055	0.37	29	0.019	0.001 254	0.021	0.004 092	0.086	0.007 97
Cygnus A	CD	0.056	13	29	0.11	0.000 005	0.12	0.000 06	0.21	0.000 927
Sersic 159/03	CD	0.058	7.8	17	0.11	0.001 518	0.16	0.001 808	0.4	0.005 59
A 133	CD	0.06	6.2	20	0.093	0.001 518	0.12	0.003 226	0.21	0.021 094
A1795	CD	0.063	1.6	23	0.044	0.001 084	0.054	0.001 808	0.14	0.005 59
A2029	CD	0.077	0.87	60	0.02	0.000 242	0.015	0.000 365	0.073	0.002 465
A478	CD	0.081	1	26	0.033	0.000 05	0.038	0.000 003	0.12	0.000 667
A2597	CD	0.085	0.67	8.6	0.047	0.000 136	0.093	0.000 181	0.18	0.001 808
3C388	CD	0.092	2	17	0.057	0.000 276	0.081	0.001 084	0.17	0.004 092
PKS0745 -191	CD	0.103	17	31	0.12	0.000 407	0.13	0.000 822	0.21	0.003 646
Hercules A	CD	0.154	3.1	20	0.066	0.001 808	0.086	0.002 124	0.17	0.005 59
Zw2701	CD	0.214	60	17	0.31	0.000 545	0.44	0.000 927	0.4	0.003 646
MS0735.6 +7421	CD	0.216	69	20	0.31	0.012 393	0.41	0.025 834	0.38	0.021 094
4C55.16	CD	0.242	4.2	14	0.09	0.012 393	0.14	0.022 226	0.22	0.018 933
A1835	CD	0.253	18	54	0.1	0.001 015	0.076	0.002 465	0.16	0.006 144
Zw3146	CD	0.291	58	74	0.15	0.001 254	0.1	0.000 723	0.19	0.003 226
注：表中 (1) 源; (2) 类型; (3) 红移; (4) 喷流中电子束功率; (5) 黑洞质量部分来源于文^[13]及文^[14]，其余均源于NED 网络数据库; (6) 爱丁顿磁场条件下的自旋; (7) 爱丁顿磁场条件下的自旋能量; (8) 静磁场条件下的自旋; (9) 静磁场条件下的自旋能量; (10) 与自旋有关的磁场条件下的自旋; (11) 与自旋有关的磁场条件下的自旋能量 (运用(6)式计算得出) Notes: The meanings of the columns are as follows. Column (1): Source name. Column (2): AGN type. Column (3): Redshift value. Column (4): Power of the electron beam in the jet. Column (5): Mass value of the black hole. Column (6): Spin of the black hole with B=B_EDD assumed. Column (7): Spin energy of the black hole with B=B_EDD assumed. Column (8): Spin of the black hole with B=10⁴G assumed. Column (9): Spin energy of the black hole with B=10⁴G assumed. Column (10): Spin of the black hole with B∝j_M assumed. Column (11): Spin energy of the black hole with B∝j_M assumed.

表选项

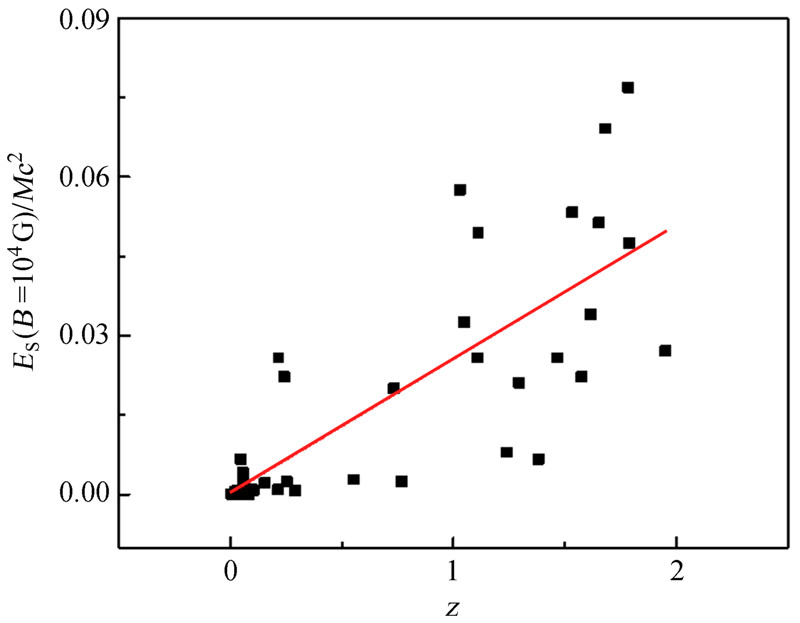
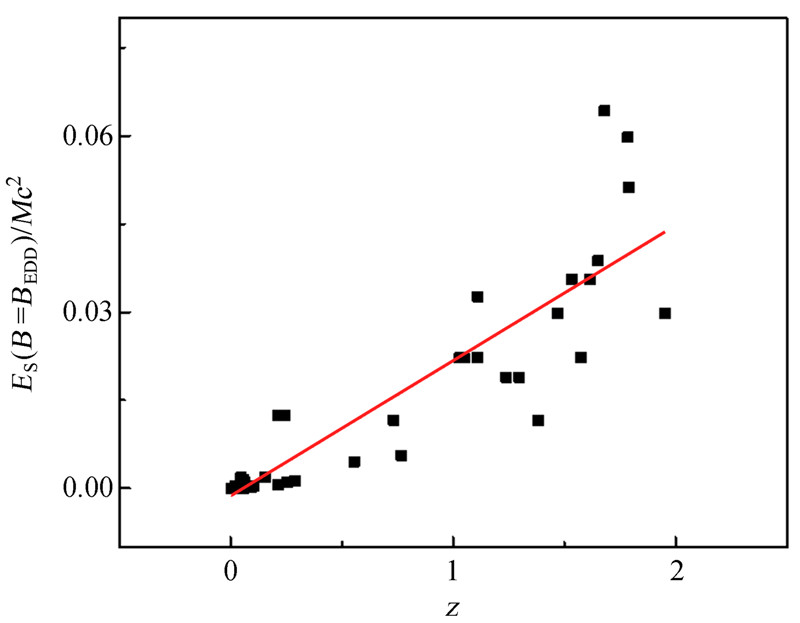
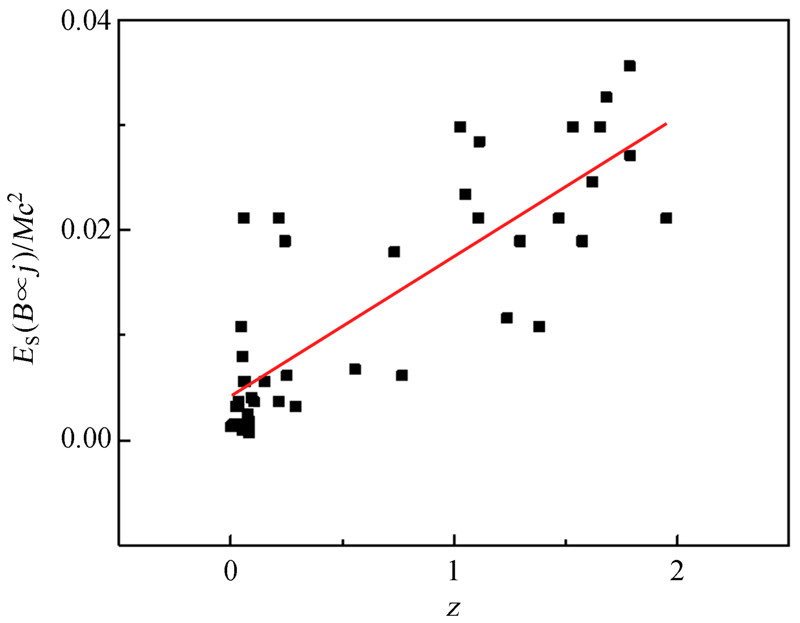
在考虑黑洞质量的情况下，由图 1、2、3可以看出E_S/Mc²与红移z分别在B=B_EDD、B=10⁴G、B∝j 3种磁场情况下具有较高的相关性。说明黑洞的自旋能量和红移z都存在联系，红移z与黑洞自旋能量在总体上的关联紧密。自旋能量与红移的关系满足Blazar的一些基本观测特征。

图 1 E_S/Mc²与红移z的相关性(B=B_EDD) Fig. 1The correlation between redshifts and E_S/Mc²

(with B=B_EDD assumed) of the black holes

图选项

图 2 E_S/Mc²与红移z的相关性(B=10⁴G) Fig. 2The correlation between redshifts and E_S/Mc²

(with B=10⁴G assumed) of the black holes

图选项

图 3 E_S/Mc²与红移z的相关性(B∝j) Fig. 3The correlation between redshifts and E_S/Mc² (with B∝j_M assumed) of the black holes

图选项

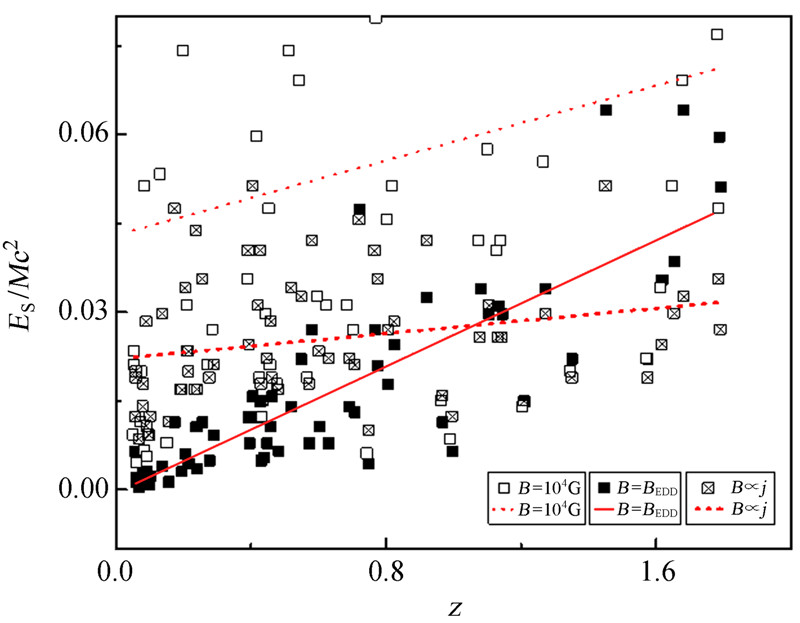
如图 4射电星系E_S/Mc²与红移z在3种不同磁场下均存在一定相关性。在爱丁顿磁场(B=B_EDD)条件下射电星系的E_S/Mc²与红移z存在强相关性。但在B=10⁴G与B∝j两种磁场条件下，射电星系E_S/Mc²与红移z有弱相关性。但总体上射电星系E_S/Mc²与红移z存在正比关系，说明黑洞的自旋能量随红移z的增大而增加。这与文^[1]的研究结果相同。

图 4 RG类黑洞E_S/Mc²与红移z的相关性 Fig. 4The correlation between redshifts and E_S/Mc² of the black holes in RG-type AGN

图选项

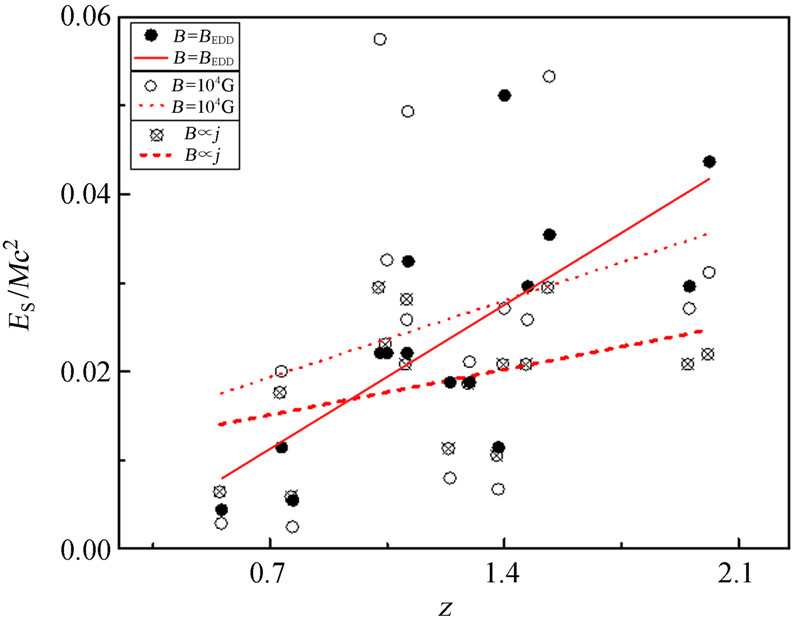
如图 5射电噪类星体(RLQ)的E_S/Mc²与红移z的相关性与射电星系(RG)相比较低，但数据整体趋势非常相似。射电噪类星体(RLQ)E_S/Mc²与红移z在3种不同磁场下均存在一定相关性。在B=B_EDD磁场条件下，射电噪类星体(RLQ)E_s/Mc²与红移z存在强相关性。但在B=10⁴G与B∝j两种磁场条件下，射电噪类星体E_S/Mc²与红移z有弱相关性。但总体上射电星系(RG)的E_S/Mc²与红移z存在正比关系，说明黑洞的自旋能量随红移z的增大而增加。这与文^[1]的研究结果也是相同的。

图 5 RLQ类黑洞E_S/Mc²与红移z的相关性 Fig. 5The correlation between redshifts and E_S/Mc² of the black holes in RLQ-type AGN

图选项

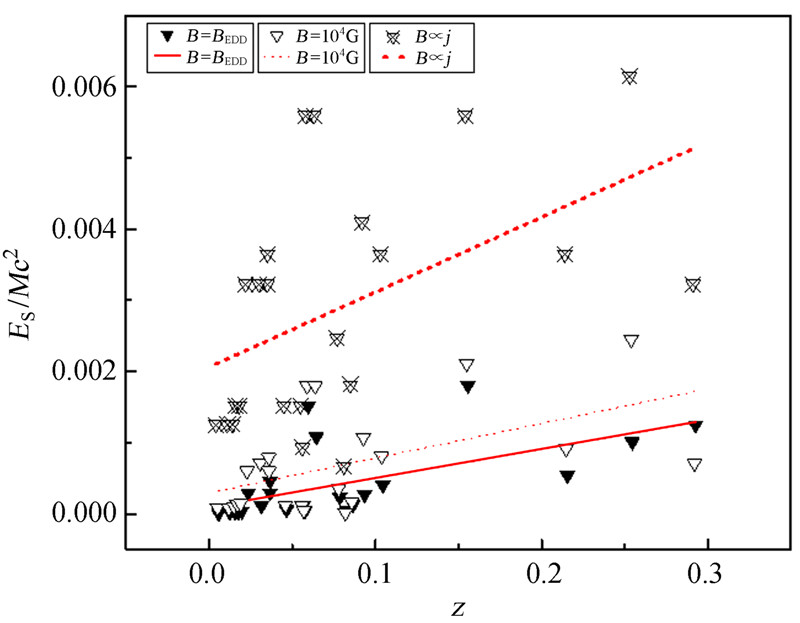
如图 6，核占优星系(CD)的E_S/Mc²与红移z在3种不同磁场的相关性均存在相关性。在B=B_EDD，B=10⁴G，B∝j 3种磁场条件下，核占优星系(CD)的E_S/Mc²与红移z均存在较明显的相关性。说明核占优星系(CD)的黑洞自旋能量在3种磁场条件下均与红移z存在较为直接的关联。

图 6 cD类黑洞E_S/Mc²与红移z的相关性 Fig. 6 The correlation between redshifts and E_S/Mc² of the black holes in cD-type AGN

图选项

不同条件下黑洞自旋能量与红移的相关性的详细分析数据如表 2。总体上E_S/Mc²均与红移z存在相关性。自旋能量随红移z的增大而增加，与文^[1]的研究结论相同。

表 2 不同条件下黑洞自旋能量与红移的相关性数据 Table 2 Results of the correlations between spin energies and redshifts of the black holes in different types of AGN under different assumptions of B

X	Y	N	R Value	Prob>F	Value (Intercept)	Value (Slope)	Error (Slope)	B	类型
Z	E_S/Mc²	112	0.802	0	-0.001 4	0.023	0.001 7	B=B_EDD	—
Z	E_S/Mc²	112	0.827	0	0.000 2	0.025	0.002 8	B=10⁴G	—
Z	E_S/Mc²	112	0.827	0	0.004 2	0.013	0.001 8	B∝j	—
Z	E_S/Mc²	67	0.84	0	0.002 2	-0.027	-0.000 3	B=B_EDD	RG
Z	E_S/Mc²	67	0.142	0.259	0.042 9	0.016	0.013 9	B=10⁴G	RG
Z	E_S/Mc²	67	0.243	0.051	0.022 1	0.005	0.002 7	B∝j	RG
Z	E_S/Mc²	11	0.712	0.003	-0.004 8	0.023	0.006 4	B=B_EDD	RLQ
Z	E_S/Mc²	11	0.293	0.29	0.010 7	0.012	0.011 2	B=10⁴G	RLQ
Z	E_S/Mc²	11	0.396	0.144	0.010 2	0.007 32	0.004 7	B∝j	RLQ
Z	E_S/Mc²	27	0.601	0.002	0.000 1	0.004 07	0.001 2	B=B_EDD	CD
Z	E_S/Mc²	27	0.529	0.009	0.000 3	0.004 87	0.001 7	B=10⁴G	CD
Z	E_S/Mc²	27	0.492	0.017	0.002 1	0.010 54	0.004	B∝j	CD
注：表中类型“—”表示本文中RG,RLQ,cD 3种类型均考虑的总体情况 Notes: The sign‘—’means the results are for all AGN types (RG,RLQ,and cD) combined

表选项

3 结论

由于射电噪类星体(RLQ)及核占优星系(CD)的样本数量较少，可能对黑洞自旋能量与红移的相关性分析产生一定的误差。要进一步详细探讨黑洞自旋能量与红移的相关性以及测定自旋能量与红移的关系公式，就需要更多的观测数据来验证本文的研究结果。

本文依据文^[14]与文^[1]的黑洞质量、中子束功率及磁场强度等运用(1)式(Blandford & Znajek^[13] Blandford^[28]；Meier^[12]；Narayan^[21])依次计算出3种磁场条件下的自旋j，后运用(3)式计算出对应的E_S/Mc²(其中自旋、黑洞、磁场测量值均独立于红移)，并依据文^[2]和文^[6]的模型，对黑洞自旋能量进行估算。最后对黑洞自旋能量与红移进行相关性分析。

本文结果表明Blazar的黑洞总体自旋能量与红移存在关系，尤其以在爱丁顿磁场条件下(B=B_EDD)最为明显。黑洞自旋能量在3种不同类型的磁场条件下(B=B_EDD，B=10⁴G，B∝j)的趋势均较为相似，呈现正比关系。实验结果与文^[1]得出的结论相同。说明Blazar黑洞自旋能量与红移存在较直接的联系。这为依据红移与自旋能量的关系，估算Blazar自旋能量提供了依据。黑洞自旋和质量的变化在二元合并时是共同发生的，随着合并的发生其自旋速度降低。由于黑洞自旋能量与AGN红移的相关性，可推断黑洞自旋能量能如同红移一样可以对AGN黑洞的合并吸积历史进行一定的描绘。

参考文献

[1]	Daly R A, Sprinkle T B. Black hole spin properties of 130 AGN[J]. Monthly Notices of the Royal Astronomical Society, 2014, 438(4): 3233-3242.

[2]	Hughes S A, Blandford R D. Black hole mass and spin coevolution by mergers[J]. The Astrophysical Journal Letters, 2003, 585(2): L101-L104.

[3]	Volonteri M, Rees M A. Rapid growth of high redshift black holes[J]. The Astrophysical Journal, 2005, 633(2): 624-629.

[4]	King A R, Pringle J E. Fuelling active galactic nuclei[J]. Monthly Notices of the Royal Astronomical Society, 2007, 385(3): 1621-1627.

[5]	Volonteri M, Sikora M, Lasota J P. Black-hole spin and galactic morphology[J]. The Astrophysical Journal, 2007, 667(2): 704-713.

[6]	Berti E, Volonteri M. Cosmological black hole spin evolution by mergers and accretion[J]. The Astrophysical Journal, 2008, 684(2): 822-828.

[7]	Zhang S N, Cui W, Chen W. Black hole spin in X-ray binaries: observational consequences[J]. The Astrophysical Journal, 1997, 482(2): L155-L158.

[8]	McClintock J E, Narayan R, Steiner J F. Black hole spin via continuum fitting and the role of spin in powering transient jets[J]. Space Science Reviews, 2013, 2(1): 256-258.

[9]	Steiner J F, McClintock J E. Measuring black-hole spin and modeling the jet dynamics in microquasar XTE J1550-564[J]. Monthly Notices of the Royal Astronomical Society, 2011, 416(1): 941-946.

[10]	Richardson G A, Nishikawa K I. Simulations of relativistic jet formation[J]. The Astrophysical Journal, 1999, 35: 1333.

[11]	Blandford R D. Spectrum of a radio pulse from an exploding black hole[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(2): 489-498.

[12]	Schmoll S, Miller J M, Volonteri M, et al. Constraining the spin of the black hole in Fairall 9 with Suzaku[J]. The Astrophysical Journal, 2009, 703(2): 2171-2176.

[13]	Daly R A. Estimates of black hole spin properties of 55 sources[J]. Monthly Notices of the Royal Astronomical Society, 2011, 414(2): 1253-1262.

[14]	Reynolds C S, Garofalo D, Begelman M C. Trapping of magnetic flux by the plunge region of a black hole accretion disk[J]. The Astrophysical Journal, 2006, 651(2): 1023-1030.

[15]	Tatum M M, Turner T J, Miller L, et al. The global implications of the hard X-ray excess in type 1 AGN[J]. The Astrophysical Journal, 2012, 762(2): 80-108.

[16]	Tchekhovskoy A, Narayan R, McKinney J C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole[J]. Monthly Notices of the Royal Astronomical Society, 2011, 418(1): L79-L83.

[17]	Thorne K S, Price R H, MacDonald D A. Book-review-black-holes-the membrane paradigm[J]. The Astrophysical Journal, 1990, 311(2): 122.

[18]	Nardini E, Fabian A C, Walton D J. Investigating the reflection contribution to the X-ray emission of Ton S180[J]. Monthly Notices of the Royal Astronomical Society, 2012, 423(4): 3299-3307.

[19]	Zoghbi A, Fabian A C, Uttley P, et al. Broad iron L-line and X-ray reverberation in 1H0707-495[J]. Monthly Notices of the Royal Astronomical Society, 2010, 401(1): 2419-2432.

[20]	Daly R A. Bounds on black hole spins[J]. The Astrophysical Journal Letters, 2009, 696(1): L32-L33.

[21]	Narayan R, McClintock J E. Observational evidence for a correlation between jet power and black hole spin[J]. Monthly Notices of the Royal Astronomical Society, 2011, 419(1): L69-L73.

[22]	Blandford R D, Netzer H, Woltjer L. Active galactic nuclei [M]. New York: Springer-Verlag, 1990.

[23]	Punsly B, Coroniti F V. Relativistic winds from pulsar and black hole magnetospheres[J]. The Astrophysical Journal, 1990, 350(2): 518-535.

[24]	Rees M J. Black hole models for active galactic nuclei[J]. Annual Review of Astronomy and Astrophysics, 1984, 22(1): 471-506.

[25]	King A R. Black hole outflows[J]. Monthly Notices of the Royal Astronomical Society, 2010, 402(1): 1516-1522.

[26]	Daly R A, Mory M P, Guerra E J. High-redshift radio galaxies as a cosmological tool: exploration of a key assumption and comparison with supernova results[C]//American Institute of Physics Conference Proceedings. 2002: 87-94.

[27]	Allen S W, Dunn R J H, Fabian A C, et al. The relation between accretion rate and jet power in X-ray luminous elliptical galaxies[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(1): 21-30.

[28]	Merloni A, Heinz S. Measuring the kinetic power of active galactic nuclei in the radio mode[J]. Monthly Notices of the Royal Astronomical Society, 2007, 381(2): 589-601.

由中国科学院国家天文台主办。

文章信息

张旭, 张雄

Zhang Xu, Zhang Xiong

Blazar黑洞自旋能量与红移相关性研究

A Study of Correlations between Redshifts and Spin Energies of Black Holes in AGN

天文研究与技术, 2015, 12(3): 253-261.

ASTRONOMICAL RESEARCH & TECHNOLOGY, 2015, 12(3): 253-261.

文章历史

收稿日期：2014-10-12

文章信息

文章历史

工作空间