2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
早期的射电天文数据处理采用模拟数据终端,结构简单且造价相对便宜,如1951年Ewen和Purcell首次发现来自银河系中心的中性氢谱线所用的模拟终端[1];乌鲁木齐天文站1998年研制的用于脉冲星观测的模拟多通道消色散终端等。与模拟终端相比,数字终端具有处理方式灵活、性能稳定、可移植性好、易于升级的特点,且更容易存储大量数据。随着电子以及计算机技术的发展,数字终端已经成为射电望远镜终端的主流技术。如2007年安装在青海德令哈观测基地的由紫金山天文台研制的 “数字FFT频谱及配套中频系统”;云南天文台与北京大学合作研制的0.7~1.4GHz分米波自相关型宽带频谱仪[2];上海天文台研制的数字滤波和数字基带转换器(Digital Base-band Converter,DBBC)[3];美国国立射电天文台GreenBank射电望远镜的VEGAS多用途数字终端等。
本文对滤波的基本原理和滤波器性能优化的方法做了回顾,并对多相滤波技术在多通道频谱分析中的应用做了说明。同时对计算量进行了分析,由于多相滤波进行了降采样操作,故节省了计算量,在射电天文频谱观测中得到了广泛应用。本文采用多相滤波技术在CASPER研制的终端开发平台上设计和实现了一个观测带宽为400MHz,通道数16k的数字频谱终端,该终端可应用于FAST河外中性氢巡天观测①。
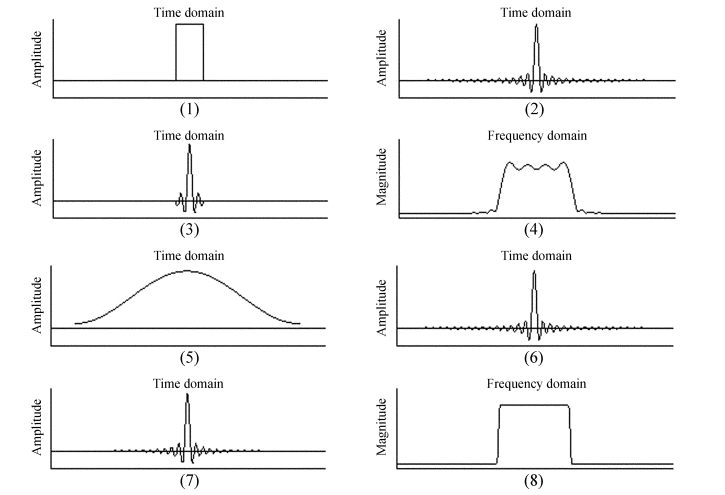
1 滤波和多通道频谱分析基本原理 1.1 滤波基本原理回顾滤波是在频域上对数据进行选择,带通滤波器形状为矩形的滤波函数使得通带内的信号不失真地通过滤波器,通带外的信号则被滤掉。当滤波器作用于信号时,在频域上实现的操作为信号的频域响应和带通滤波器的 “矩形” 频域响应相乘,对应在时域上的操作为信号和带通滤波器时域函数的卷积。在实际操作中,往往对 “矩形” 滤波器的时域sinc函数做一定长度的截取(见图 1(1)至图 1(3)),并用这个截取后的sinc函数和输入信号卷积。此时由于对频域 “矩形” 滤波器的时域函数进行了截取,频域的滤波器性能发生了变化。根据卷积定理,时域上无限长的sinc函数和截断函数(这里为矩形窗)的相乘对应到频域的操作为二者对应的频域响应的卷积,这里即为 “矩形” 滤波器和一个sinc函数(截断函数矩形窗对应的频率响应)的卷积。与 “矩形” 滤波器相比,此时得到的滤波函数的频域响应不再为矩形,出现过渡带和震荡,存在频谱泄露现象② (见图 1(4))。
|
| 图 1(1) 为一个矩形窗函数,起到对序列进行截断的作用;(2)为一个无限长的sinc函数,其频域响应为一个频域矩形函数;(3)对图 1(2)的无限长的sinc函数采用图 1(1)的矩形窗相乘进行截断操作后得到的序列;(4)为图 1(3)截断序列所对应的频域响应,有较大震荡和较宽过渡带,存在频谱泄露现象。(5)为加长的窗函数(此处为汉明窗);(6)为无限长的sinc函数;(7)为加长的窗函数和无限长sinc函数相乘得到的序列;(8)为图 1(7)对应序列的频域响应,经过加长序列和采用窗函数后,震荡和过渡带减小,频域响应性能得到改善 Fig. 1 llustration of bandpass filtering. The panel (1) is a plot of a rectangular window to truncate a signal sequence. The panel (2) is a plot of an infinitely long signal sequence which is a sinc function of time. In the frequency domain,the sequence is a top-hat function. The panel (3) is a plot of the result of multiplying the window in (1) and the sequence in (2). The panel (4) is a plot of the function of the signal sequence in (3) in the frequency domain. There are strong ripples and wide transition ranges in the frequency-domain function,showing obvious signal leak in the frequency domain. The panel (5) is a plot of a window function wider than the window in (1). Here,the Hamming window is used as the example. The panel (6) is a re-plot of (2). The panel (7) is a plot of the result of multiplying the window in (5) and the sequence in (6). The panel (8) is a plot of the function in (7) in the frequency domain. The result in (8) is improved compared to that in (4) with the ripples weakened and the transition ranges reduced |
为了改善该滤波函数的频域带通性能,可以加长其时域函数截断长度(即矩形窗长度)。此时截断函数(矩形窗)的频率响应sinc函数的主瓣变窄,使得滤波函数通带形状更接近矩形,但吉布斯现象增强;可以选择其他合适的窗函数(如汉明窗)改善,得到较好的滤波性能(见图 1(5)至1(8))。汉明窗和矩形窗的频率响应对比如图 2,频域采用归一化频率,可以看出汉明窗的频域响应旁瓣抑制(约-50dB)较矩形窗的旁瓣抑制(约-15dB)要好,但其主瓣宽度较宽。
1.2 多通道输出和多相滤波基本原理射电天文中频谱观测往往需要在一定的频率范围内做多个通道,并获取每个通道的功率。根据帕斯瓦尔定律,要获取每个通道的功率,不需要得到每个通道内的时域函数,而是通过得到通道内的频域函数的均值后,直接进行平方运算得到功率[4]。取通道带宽对应的 “矩形” 滤波器,进行傅里叶逆变换后得到时域的sinc函数,输入信号与该函数相乘后进行傅里叶变换得到频域 “矩形” 滤波器和输入信号频谱的卷积,得到的卷积值即为 “矩形” 滤波器通带内的输入信号频谱的平均值。将得到的频域上的卷积值以通带带宽为间隔取样,取平方后,得到多通道输出的功率谱。
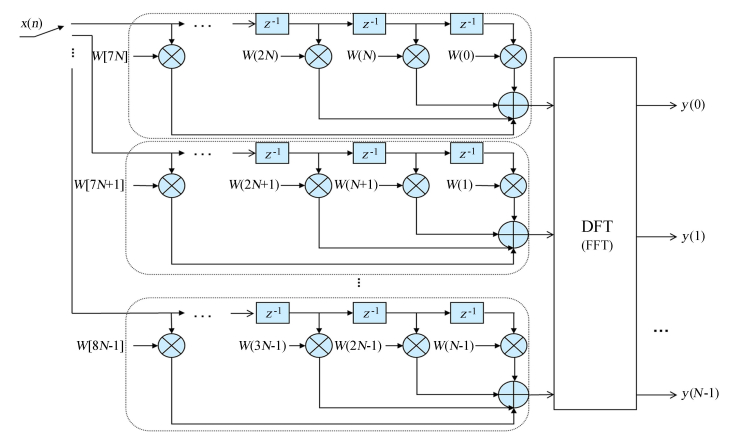
对于满足奈奎斯特采样定理的采样频率为fs的离散序列,取N个时域数据进行快速傅里叶转换后可以得到N个频域数据。N个频域数据即为在原频谱与一个主瓣宽度为2fs/N的sinc函数卷积上的间距为fs/N的采样,通过取平方运算后可以得到包括各个频点的带通为主瓣宽度2fs/N sinc函数内的功率。为了改善通道带通性能形状,可以在时域乘以频率通道带宽为fs/N的 “矩形” 滤波器函数对应到时域上的sinc函数。但因时域上矩形窗长度的限制,通道形状难以 “矩形”。为了获得上述 “矩形” 通道的性能,需要增加时域矩形窗的长度,对时域上的sinc函数取更长的序列(如8倍的N/fs,见图 1(7)),再进行快速傅里叶变换运算后得到更多的数据点(8倍,见图 1(8))。此时的通道函数频域响应为加长的矩形窗函数和sinc函数各自的频域响应的卷积结果。通过改变时域矩形窗的长度,选择不同的窗函数可以改善通道形状,从而影响每个通道的平坦度和矩形系数。由于只加长了时域sinc函数截断长度,其主瓣宽度并未改变,所以通道带宽仍为fs/N。但此时的频域数据量为原来的8倍,相邻数据点之间间隔为fs/8N ,因此只需要进行8倍降采样即可得到通道带宽为fs/N频域数据。多相滤波[5, 6]即为实现该计算的一种手段。与对加长窗长度和改变窗函数的序列直接进行8N个点的快速傅里叶变换相比,多相滤波计算量大大减少;而与采用矩形窗只进行N个点的快速傅里叶变换相比,计算量增加也不多(见表 1),其硬件实现结构如图 3。
| 直接 N点FFT | 8 N点加窗序列FFT | (多相滤波结构+FFT) | |
| FFT乘法计算量 | Nlog 2 N | 8 Nlog 28 N | Nlog 2 N |
| 加窗乘法计算量 | 0 | 8 N | 8 N |
| 乘法总计算量 | Nlog 2 N | 8 N+8 Nlog 28 N | 8 N+Nlog 2 N |
|
| 图 3 多相滤波硬件实现结构图 Fig. 3 A structural diagram of the hardware of the Polyphase Filter Bank |
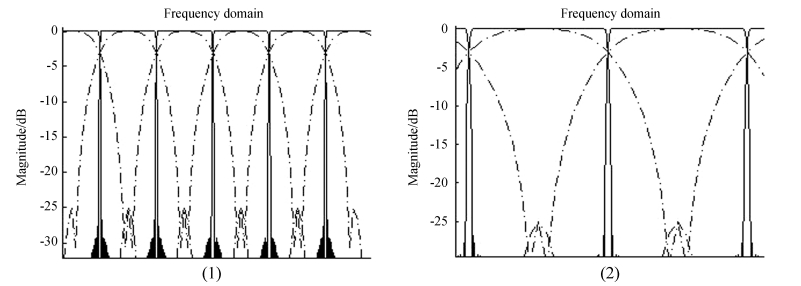
如上两节所述,通过改变时域sinc函数截取长度和选择不同的窗函数可以改善通道带通性能。图 4(1)展示了采用相同的时域汉明窗和相同的时域sinc函数的情况下,只改变sinc函数的截取长度,在符合奈奎斯特采样定理要求下用相同采样率分别取一个主瓣长度的时域sinc函数(虚线)和16倍主瓣长度的时域sinc函数(实线)所对应的多相滤波的通道形状。图 4(2)是对两个相邻通道交叠处的放大。当sinc函数截取长度越长时,对应的通道函数越趋近于矩形。时域sinc函数相同,故时域主瓣宽度保持不变,因此对应的频域通道的宽度也相同。当时域的矩形窗足够长时,相邻通道的频谱响应的交叠点大致相同(在-3dB左右)。
|
| 图 4 不同截取长度和不同主瓣宽度的sinc函数对频域通带形状的影响 Fig. 4 Plots showing the frequency-domain functions of (time-domain) sinc-form signal sequences of different truncation lengths and main-lobe widths |
和直接快速傅里叶变换相比,由于多相滤波的降采样处理,计算量大大减少,在射电天文数据处理方面得到了广泛的应用。国内云南天文台、上海天文台、国家天文台太阳射电团组等都对该技术进行了研究和应用。美国UC Berkeley的CASPER团组开发了一系列的射电天文数字终端软硬件平台,对于不需了解底层硬件的天文学家是一个不错的选择,FAST终端开发将采用该平台。本文在CASPER终端平台上实现了一个观测带宽为400MHz、通道数16k,可通过10GbE网卡传输数据的数字终端。该终端可在FAST多波束河外中性氢巡天中得到应用。河外中性氢巡天观测的需求如下:
带宽:400MHz,观测中性氢红移从0到0.26,频率范围为1050MHz~1450MHz。
采样精度:8bits。
通道数:12k。
河外中性氢观测速度分辨率应达到10km/s,结合带宽,通道数为
| \[{\rm{400MHz/1050MHz}} \times \frac{{10{\rm{km/s}}}}{{3000000{\rm{km}}/{\rm{s}}}} \approx 12{\rm{k}}.\] | (1) |
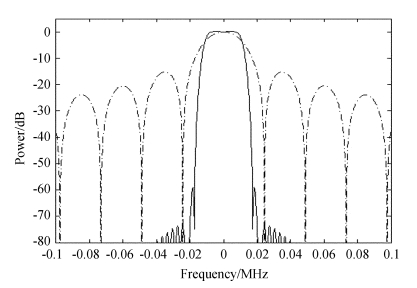
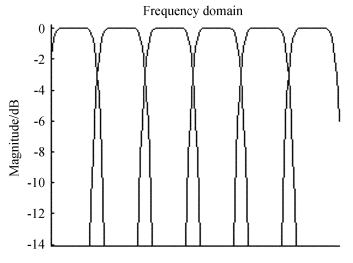
在设计中,多相结构(Polyphase Filter Bank,PFB)的通道形状如图 4中实线,直接快速傅里叶变换的通道形状为图 5中虚线。设计中多相结构的窗长度是直接进行快速傅里叶变换的矩形窗长度的8倍。多相结构第一旁瓣抑制约-60dB,快速傅里叶变换第一旁瓣抑制约为-15dB。取矩形系数为3dB带宽和60dB带宽的比值(越接近1越好),则多相结构的矩形系数为0.63,快速傅里叶变换的矩形系数为0.42,多相结构通带形状更优。图 6展示了设计中的几个通道形状。
|
| 图 5 多相结构和快速傅里叶变换的单个通道频域响应 Fig. 5 Single-channel frequency responses of the PFB and FFT |
|
| 图 6 设计中多通道形状展示 Fig. 6 Multi-channel frequency responses of the PFB in our design |
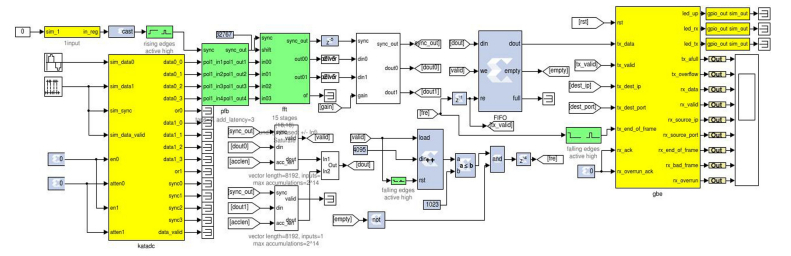
该多通道数字终端在MATLAB/Simulink环境下进行仿真设计,利用MATLAB和Xilinx开发的System Generator[7]将mdl③文件 “翻译” 成硬件语言运行,通过python语言操作硬件模块实现显示和存储。mdl文件截图见图 7。
|
| 图 7 硬件设计图 Fig. 7 A system diagram for the multi-channel digital backend in our design |
信号处理流程为:400MHz的模拟信号首先经过模拟数字转换器采样输出量化比特数为8bit的数字信号;之后数字信号经过所设计的多相滤波和傅里叶变换相结合的多通道结构实现多通道输出,最后将输出频谱数据经过累加后显示并通过10GbE网卡传送到其他设备上存储。
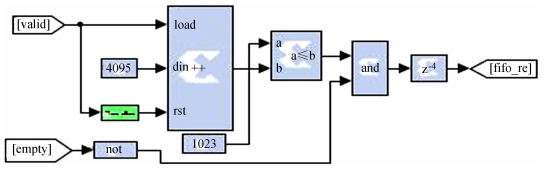
现场可编程门阵列时钟频率为200MHz,而10GbE网卡工作频率为156.25MHz,最大缓存空间为8704Bytes。接口工作在异步模式下,若不加控制直接将现场可编程门阵列处理数据不断地传送给10GbE模块,缓存最终将溢出。现场可编程门阵列的频谱数据是以突发数据包(burst)的形式向10GbE模块传送并且每条频谱的大小(213×8B=216B)超过最大缓存空间。利用两个突发数据包之间的间隔的累加时间,可以采用先进先出模块(First In First Out,FIFO)[8]解决这个问题。每个突发数据包先存放在先进先出模块中,再由先进先出模块向10GbE模块发送传送请求,传送数据大小由先进先出模块控制,可以将一条频谱数据分成8次(23次)传输给10GbE,逻辑控制模块如图 8。先进先出模块每次向10GbE模块传送一个突发数据包中的210个数据,等待(212-210)个时钟后(给10GbE模块足够的传送时间),传送第2次210个数据,再等待(212-210)个时钟,以此类推,直到传送第1个突发数据包中的最后一组210个数据。结合输入先进先出模块的有效信号valid以及FIFO本身的空信号进行其他的逻辑控制,最终形成了图 8的传送逻辑控制模块。
|
| 图 8 FIFO传送逻辑控制模块 Fig. 8 A system diagram of the FIFO logic-control module for data transmission |
10GbE模块[9]采用UDP协议[10]通过以太网传送数据包给指定服务器。输入数据比特数为64,设定好目的ip和目的端口后,通过tx_valid置1输入数据,在输入数据的最后一个时钟同时将tx_end_of_frame置1完成一次数据输入,并进行UDP封装后传送向目的ip和端口。在目的ip处,可通过Wireshark Network Analyzer监测和查看收到的UDP包,并通过程序将UDP封装的头部文件去除后以二进制文件格式存储在指定目录下。
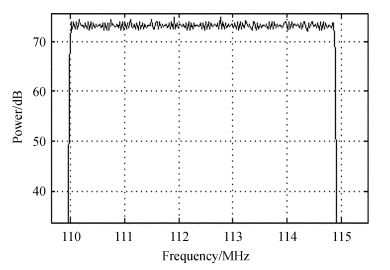
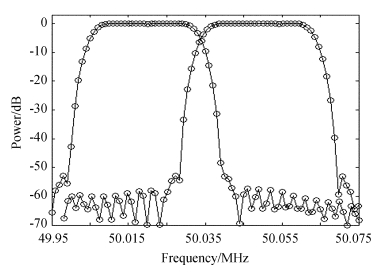
2.1 多通道频谱数字终端的测试测试实验中使用安捷伦N5181A信号发生器进行扫频来测试该终端的性能。信号发生器设置为步进频率自动单次扫描模式,输出信号功率为0dBm,每个单频信号持续时间500ms。信号源输出的信号传给模拟数字转换器,经模拟数字转换器采样后传送给数字信号处理板卡ROACH进行多相滤波处理。图 9从下至上依次为安捷伦N5181A信号发生器、控制服务器和终端开发平台。图 10扫频频段为110MHz~115MHz,积分时间0.0253s。图 11为当输入单频信号从49.95MHz递增至50.1MHz(步进为0.001MHz),第2049和2050两个通道(由左及右)的输出值变化情况,由此可以扫出通道的形状。该设计采用8段数据,每段数据的长度为214个点,由于纵坐标采用功率值,故交叠点在-6dB位置。

|
| 图 9 扫频测试系统 Fig. 9 A picture of the system for the frequency-sweep test |
|
| 图 10 扫频测试 Fig. 10 A plot showing the result of the frequency-sweep test |
|
| 图 11 通道形状图 Fig. 11 The frequency responses of two channels resulting from the frequency-sweep test |
本文回顾了滤波的基本原理,分析了滤波器性能优化方法,并对多相滤波技术在多通道频谱分析中的应用做了说明。通过增加时域矩形窗的长度和额外加窗函数的方法,可对滤波器带通性能进行优化。与直接快速傅里叶变换相比,多相滤波器由于在时域上采用了更长的矩形窗,其滤波通道性能得到很大改善,但计算量增加不多。在UC Berkeley的CASPER团组研制的终端开发平台上利用多相滤波技术实现了一个观测带宽为400MHz,通道数16k的数字终端,并完成了频谱的生成显示和10GbE的传输。该终端可应用于FAST多波束河外中性氢巡天观测。
| [1] | Ewen H I, Purcell E M. Observation of a line in the galactic radio spectrum: radiation from galactic hydrogen at 1 420 Mc./sec [J]. Nature, 1951, 168: 356. |
| [2] | 陈敬英, 王书浩, 夏志国, 等. 云南天文台太阳射电频谱仪的网络系统[J]. 云南天文台台刊, 2000(1): 41-48. Cheng Jingying, Wang Shuhao, Xia Zhiguo, et al. The network system of solar radio spectrographs at Yunnan Observatory[J]. Publications of Yunnan Observatory, 2000(1): 41-48. |
| [3] | 项英, 张秀忠. 数字滤波技术在射电天文测量中的应用[J]. 天文学进展, 2004, 22(2): 95-103. Xiang Ying, Zhang Xiuzhong. Application of digital filtering in radio astronomy[J]. Progress in Astronomy, 2004, 22(2): 95-103. |
| [4] | 董亮, 汪敏, 苗爱敏, 等. 基于FPGA嵌入式的多通道功率监测处理器设计[J]. 电子测量技术, 2010, 33(3): 58-63+105. Dong Liang, Wang Min, Miao Aimin, et al. Multi-channel power detecting processor's designing based on FPGA embedded system[J]. Electronic Measurement Technology, 2010, 33(3): 58-63+105. |
| [5] | 陈岚, 张秀忠. 用于VLBI数字基带转换的多相滤波技术研究[J]. 天文学进展, 2008, 26(1): 87-94. Chen Lan, Zhang Xiuzhong. The study of DBBC based on poly-phase filter banks and FFT in VLBI[J].Progress in Astronomy, 2008, 26(1): 87-94. |
| [6] | 朱凯, 甘恒谦, 朱岩, 等. 多相滤波器组谱分析方法的性能讨论与天文观测应用[J]. 天文研究与技术——国家天文台台刊, 2011, 8(1): 81-90. Zhukai, Gan Hengqian, Zhu Yan, et al. On the performance of spectral analysis with a polyphase filter bank and its application in radio astronomy[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2011, 8(1): 81-90. |
| [7] | 纪志成. FPGA数字信号处理设计教程[M]. 西安: 西安电子科技大学出版社, 2008. |
| [8] | 张西洋, 何乐生, 董亮, 等. 800-975 MHz太阳射电数字观测终端的设计与实现[J]. 天文研究与技术——国家天文台台刊, 2014, 11(2): 118-126. Zhang Xiyang, He lesheng, Dong Liang, et al. Design and implementation of a digital observation terminal for solar radio observation within the 800MHz-975MHz band[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(2): 118-126. |
| [9] | 刘东亮, John Ford, Glen Langston, 等. 基于IBOB的射电望远镜宽带数字频谱仪系统的设计与测试[J]. 天文研究与技术——国家天文台台刊, 2010, 7(1): 27-32. Liu Dongliang, John Ford, Glen Langston, et al. Design and test of an IBOB based wideband digital spectrometer system for a radio telescope[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2010, 7(1): 27-32. |
| [10] | 崔鹤, 刘云清, 盛家进. 基于FPGA的UDP/IP协议栈的研究与实现[J]. 长春理工大学学报: 自然科学版, 2014, 37(2): 133-137. Cui He, Liu Yunqing, Sheng Jiajin. Research and implementation on UDP/IP protocol stack base on FPGA[J]. Journal of Changchun University of Science and Technology: Natural Science Edition, 2014, 37(2): 133-137. |



