云南天文台全日面太阳黑子照相观测系统的建立[1],为进行黑子常规观测创造了(硬件)条件。在天气条件允许的情况下,拍摄不同曝光时间的全日面黑子图像,从中选取最好的一张作为数据处理对象。太阳黑子的常规观测可以长期监测黑子坐标位置、黑子相对数、黑子面积等的变化。比如当黑子群和黑子数目增多时,日面上其他各种活动现象(如光斑、谱斑、日珥、暗条及耀斑等)也会增强[2]。黑子面积的变化也体现了太阳日面活动的变化。因此,这些常规观测数据所获取的物理量对于长期研究太阳活动周期变化和预测太阳活动有着重要的意义。本文中,采用区域生长法[3]识别黑子并计算黑子平面面积和球面面积,同时运用Solar Soft Ware软件包(SSW)和IDL软件对太阳自转轴、太阳经纬度、太阳半径、日心等物理参数进行计算。
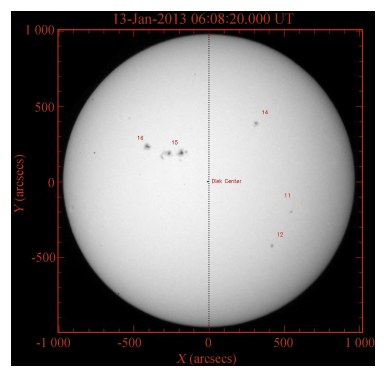
1 数据处理利用云南天文台太阳黑子望远镜在2013年01月13日(观测时间06∶08UT)获取的资料进行分析。首先去除噪声。该数据中的噪声主要来自于太阳黑子望远镜镜筒里面的灰尘,有些灰尘大小和拍摄之后的图像中呈现的特征和黑子类似,很难辨认。不过这些灰尘在每次拍摄太阳黑子像时由于快门振动而不断变换位置。所以,在连续拍摄过程中,可以判断噪声和黑子的区别,从而避开这些明显的噪声。确定图像中的黑子之后,对图像中的黑子进行分群和编号,日面中心位置的确定等处理,在此基础上绘制日面经纬度网格图,然后即可确定每个黑子(群)的日面位置。通过区域生长法计算黑子(群)的像素数并通过相关公式换算成黑子的圆面积和球面积。最后还计算了当天太阳黑子相对数,然后将统计计算出来的黑子参数进行汇总并列成表格。图 1是要处理的资料。

|
| 图 1 2013年1月13日观测的太阳黑子图像(06∶08 UT) Fig. 1 A solar image with sunspots observed at 06∶08 UT in January 13,2013 |
太阳黑子通常是以几个黑子一起成群地出现在日面上,也有以单个黑子的形式出现的,黑子群的划分一般是从黑子的形态结构和相互间的距离决定,靠近在一起而相互有“联系”的黑子,被划到一个群体。根据黑子在日面上分布的特征,黑子群的轴向(两个主黑子间的连线方向)跟日面的东西向交角一般小于5°,因此黑子(群)在纬度方向变化很小,而在日面经度方向有一定的变化。黑子群的划分有两种类型:即Zürich分类和Wilson(磁)分类,前者是由黑子的形态结构和相互间的距离决定,后者从黑子的磁场结构和特性考虑,我们使用前者分类法而不考虑它的磁场结构。按照Zürich分类法,黑子群可分为9种类型:即A、B、C、D、E、F和G、H、J。A型黑子即无半影或无双极结构的小黑子;B型是无半影的双极群;而C型和D型有双极结构,其中一个黑子有半影为C型,而两个都有半影且分开的日面距离小于10°的认定为D型黑子群;对于大型黑子群E型和F型而言,它们的两个主要黑子都有半影,而且结构复杂,它们之间还有许多小黑子,区别在于黑子群在日面东西向跨度,大于10°和大于15°分别为E型和F型。此外,有些大双极群只有几个大黑子而无小黑子,日面经度延伸大于10°的划定为G型,而只有一个黑子有半影的单极群,直径大于2.5°是H型,小于2.5°的J型。这是传统的黑子群划分方法(详细情况可参考文[2])。
运用这种传统的方法对黑子群进行划分并按黑子出现的先后顺序给每个黑子群编号。例如,2013年01月01日新出现的第1个黑子编号为1,新出现第2个黑子编号为2,以此类推(这是云南天文台自己的编号)。这里需要说明的是由于黑子强度每天有不同的变化,有些小黑子今天出现,明天可能就消失,所以黑子分群不能完全依赖计算机判断,在目前情况下还需要观测者参与判定,有时难以给黑子群编号时需要参考前一两天或后一两天的观测资料才能尽可能地给出合理的编号;例如一群黑子刚从东边缘转出时还无法判断是一群还是两群,要到第二或第三天才能看出它的全貌。
在处理的黑子图像资料中能分辨的日面黑子可划分为5个黑子群,按它们出现的次序分别编号为:11、12、14、15和16(如图 2),其中11和12两群黑子在日面南半球,14、15和16在日面北半球。
|
| 图 2 黑子分群和编号 Fig. 2 Grouping and numbering of the sunspots in |
由于地球围绕太阳的周年运动和太阳本身的自转,观测的日面图像的日轴(即太阳自转轴)和地球南北方向有个夹角(即日轴方位角)。这个夹角在一年内不断发生变化(变化范围:-26.27-+26.27)。又由于地球的绕日运动轨道和太阳赤道不在一个平面内,日面的中心(日心B0)位置在太阳像上会有一个投影效应,因此和太阳图像的中心位置(视位置)一般是不重合的。传统的日轴方位角获取方法是根据紫金山天文台编制的天文年历查询得到(以世界时0时为准),向东为正、向西为负,然后将它外推到观测时刻的P值,该P值为实际的日轴方位角。由于日轴每天的变化非常小(平均小于17′),所以在以往手工处理黑子资料时,人工判定日轴位置的误差约0.1°,因此测量黑子的经纬度、日心距离等也产生一定的误差。假设日轴方位角误差为ΔP,由它引起的经度和纬度误差分别为Δl和Δφ,因此,(ΔP)2=(Δl)2+(Δφ)2,假设Δl=Δφ,则有${\left( {\Delta l} \right)_{\max }} = \frac{1}{{\sqrt 2 }}\Delta P$,由人工确定日轴位置的最大误差(ΔP)max=0.1°,所以产生经纬度的最大误差(Δl)max=(Δφ)max=4.24′,因此,该望远镜极轴指向偏离的系统差约4′(这种考虑也适用于地平式望远镜,即地平高度和方位角的系统误差也在4′左右)。
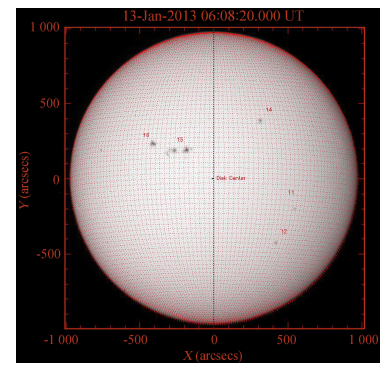
计算机处理的误差比人工方法要小得多,它跟计算方式有关(如大黑子以它的重心位置确定它的经纬度值),而P值由查表后内插得到理论值,经纬度计算的结果误差很小,在精度要求不高的情况下可以不予考虑。天文年历也给出了每天的B0值,有了P和B0即可给出日面经纬度分布图 (如图 3)。当确定日心的经纬度,并且知道每个网格间隔的度数时,便可以读取日面经纬度。在本文中,采取SSW软件包里面的程序,直接计算得出日心坐标,并建立太阳图像球面坐标系,从而获取日心位置。图 3中,已经将太阳极轴旋转过P角使太阳极轴方向跟地球南北方向一致,并将太阳的极轴用黑色虚线标出。同时画出太阳像的圆心,并通过程序计算出圆心处经纬度为(165.6°,-4.4°)。
|
| 图 3 太阳经纬度坐标图(经加密后的经纬度网格图,每网格代表 2°) Fig. 3 A refined grid of the solar longitude-latitude coordinate system with each grid element spanning 2°× 2° |
确定日面中心处的经纬度坐标后,画了日面经纬度网格图如图 3,图中分别给出每个黑子或者黑子群的日面(经纬度)坐标。经纬度网格可以精确到1°/格,比如,已经确定日面中心的经纬度(165.6°,-4.4°),编号为14的黑子可以通过其与日面中心的网格数确定其经纬度,并以黑子重心所在的位置计算黑子群的经纬度数值(145,19)。
1.4 黑子面积计算黑子面积是通过区域生长法,选取黑子中的一部分区域灰度的平均值(本影和半影)作为生长的阈值,根据灰度近似的生长准则进行生长,获取黑子面积在图像中对应的像素数。计算黑子面积时,没有使用数据平滑方法,因为数据平滑使黑子半影和光球背景的灰度更相近,这样在使用区域生长法时,增加了计算误差和黑子面积的不确定性。没有使用数据平滑的原始图像,避免黑子半影和光球背景边界更加模糊。然后根据以下公式计算黑子在太阳光球表面的圆面积A和球面积C:
A=a×n,
C=a×n×secθ,
$C = n\sum\limits_{i = 1}^a {\frac{R}{{\sqrt {{R^2} - r_i^2} }}} ,$
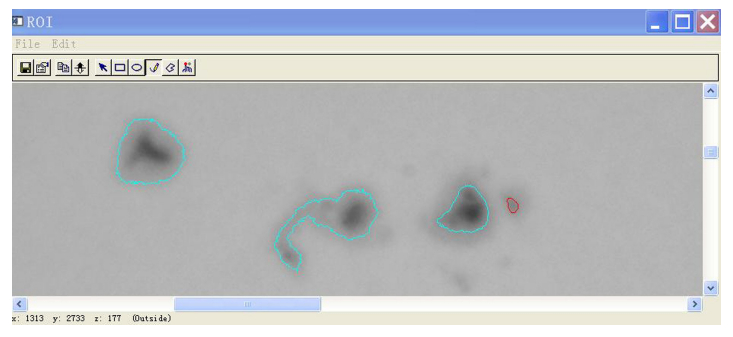
其中a为黑子所包含的像素数目;n为角分辨率的平方;ri为黑子所在区域内第i个像素到日面中心的距离;R为太阳像的半径。这里计算黑子球面积时采用逐个像素点的计算。将黑子图像放大如图 4,算出的黑子面积是以太阳半球面积的百万分之一为单位。
|
| 图 4 用于计算黑子面积的黑子放大图像 Fig. 4 An enlarged image of the sunspots to be used for area analysis |
黑子相对数是表征太阳活动强弱的指数之一。黑子相对数通常以R表示。数学表达式为
R =k(10g+f),
其中,g为日面上黑子群的总群数,这组数据中g=5;f是黑子总个数;k为换算因子,它跟观测者的经验、熟悉程度及大气质量有关,通常以瑞士苏黎世天文台观测给出的黑子相对数R值为标准,跟我们的R值作比较得到k值,它一般小于1,对于一个有经验的观测者而言,k值基本上是稳定的。用照相观测和计算机处理,不妨暂取k=1,经过几年观测和苏黎世天文台结果对比后再做调整。因此,资料中对应的黑子相对数R=57。
2 总 结将经以上方法处理得到的日面黑子资料,统计数据见表 1(其中纬度的正、负号分别表示该黑子位于北、南半球):
| 观测日期:2013-01-13 | ||||
| 黑子编号 | 黑子个数 | 黑子圆面面积 | 黑子球面面积 | 经纬度(Lon°,Lat°) |
| 16 | 1 | 170.870 | 196.592 | (190,10) |
| 15 | 1 | 272.784 | 298.781 | (181,7) |
| 15 | 1 | 132.209 | 141.637 | (176,7) |
| 15 | 1 | 7.267 | 8.503 | (174,7) |
| 14 | 1 | 54.485 | 64.959 | (145,19) |
| 12 | 1 | 55.921 | 71.676 | (135,-30) |
| 11 | 1 | 16.076 | 21.304 | (130,-16) |
| 累计 | 7 | 709.612 | 803.452 | 黑子相对数 R=57 |
综上所述,编制一定的计算程序用计算机处理黑子观测资料改变了手工处理黑子资料的传统方法,既能节省劳动力,又能提高参数计算的效率和精度,这套计算程序可正常使用,每天处理一幅图,只要将参数调整一下就可以处理另一天的观测图像,即可获取另一天的黑子参量。但经纬度在画出(经纬)网格后需由人工读取,所以在目前情况下,还不能完全依赖计算机操作,在处理资料,特别在黑子分群中需要观测者的参与和判断,有时甚至要参考前后一两天的黑子资料才能做出合理的分群判断,这关系到黑子相对数的计算。因此,即使在用计算机和相应软件处理黑子观测资料的情况下,除望远镜保持清洁状态外还要求观测者具有一定的观测经验和熟练的观测技术,这是十分必要的。
| [1] | 顾啸马, 叶惠莲, 林隽, 等. 云南天文台全日面太阳黑子照相观测系统的建立 I. 硬件部分[J]. 天文研究与技术——国家天文台台刊, 2014, 11(2): 151-156. Gu Xiaoma, Ye Huilian, Lin Jun, et al. Building of a camera system for observation of the full solar disk with sunspots in the Yunnan Observatories I. hardware[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(2): 151-156. |
| [2] | 林元章. 太阳物理导论[M]. 北京: 科学出版社, 2000: 401-412. |
| [3] | 刘艳霄, 杨云飞, 林隽. 太阳光球磁亮点的识别算法[J]. 天文研究与技术——国家天文台台刊, 2014, 11(2): 145-150. Liu Yanxiao, Yang Yunfei, Lin Jun. A region-growth algorithm to recognize magnetic bright spots in the solar photosphere[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(2): 145-150. |


