二维光纤光谱数据图像是一种特殊的信号,它由目标天体的光学能量信号经过外界环境、望远镜光学系统等在光谱仪CCD相机上投影成像。郭守敬望远镜,即大天区面积多目标光纤光谱望远镜(LAMOST)是由中国科学院国家天文台建成的施密特式光纤光谱望远镜,配备了4 000根光纤、16台光谱仪以及32台CCD相机,与同类型其它望远镜相比,性能参数有极大提高[1]。光谱能量抽取处理是二维光纤光谱数据处理中的重要环节,光谱抽取的精度直接影响后续处理的准确性。望远镜系统在观测目标星体时受到大气层扰动、光的衍射以及环境和检测噪声的影响,目标星体较亮时,由于能量较强,观测得到的光纤形状完整,可以达到较高精度的抽谱结果;目标星体较暗时(LAMOST系统需要观测星等达到20.5的暗弱天体),光谱能量较弱,观测得到的光纤光谱数据极易受到噪声影响,信噪比很低,这种情况下直接进行光谱抽取会大大降低处理精度。因此,在进行抽谱之前,需要对二维光谱数据图像进行预处理,即进行低信噪比条件下的光纤光谱信号降噪,抑制噪声,保持有效信号。本文论述的输入图像已经扣除了宇宙射线、本底和杂散光的影响。
二维光谱图像具有空间方向(即光纤排列方向)和波长方向(即色散方向),在空间方向上,每根光纤的光谱能量以点扩展函数(Point Spread Function,PSF)的形式扩散到邻近像素点,形成近似高斯分布的波形[2]。LAMOST二维光纤光谱数据处理系统(Data Processing System,DPS)①目前采用光谱图像在空间方向上的一维抽谱方法,对低信噪比的输入图像,有必要在抽谱之前进行空间方向的降噪;在波长方向上,其轮廓特征反映了该光纤获取的目标天体的光谱信息,在该方向上进行平滑滤波操作会破坏光谱信息的完整性。因此,一般研究的光谱数据降噪只在二维光谱图像的空间方向上进行[3, 4, 5]。这里为了不和波长方向的光谱轮廓概念混淆,称空间方向上的轮廓形式为光谱信号波形。
文[3]提出基于快速傅里叶变换(Fast Fourier Transform,FFT)的波形改善方法,将给定波长在空间方向上的目标观测信号进行快速傅里叶变换,设计低通滤波器去噪,由于信号和噪声在频率域存在交叉混叠,该方法滤波效果有限。文[4]结合经验模态分解(Empirical Mode Decomposition,EMD)和快速傅里叶变换进行分层削弱噪声,该算法复杂度较高,不易实现。文[5]采用Wigner变换(WT)结合低通滤波从目标信号中分离噪声,但由于Wigner变换中存在交叉项,很难把混合在信号中的噪声分量滤除。
传统滤波方法,将信号变换到频域之后直接进行低通滤波,但光纤光谱信号中的噪声分布在整个频带内,通过低通滤波器,噪声成分不能完全滤除。由于高斯轮廓信号在Wigner变换域具有时频聚集特性,而噪声没有这种聚集特性,因此在Wigner时频域提出一种新的滤波思路。首先进行初始滤波,构建带通滤波器,滤除较分散的明显噪声分量;然后在通带部分进行基于信号先验信噪比的加权滤波,根据有效信号所占比例设计加权系数,保持有效信号,抑制混叠噪声;最后利用Wigner变换的边缘特性重构有效信号。
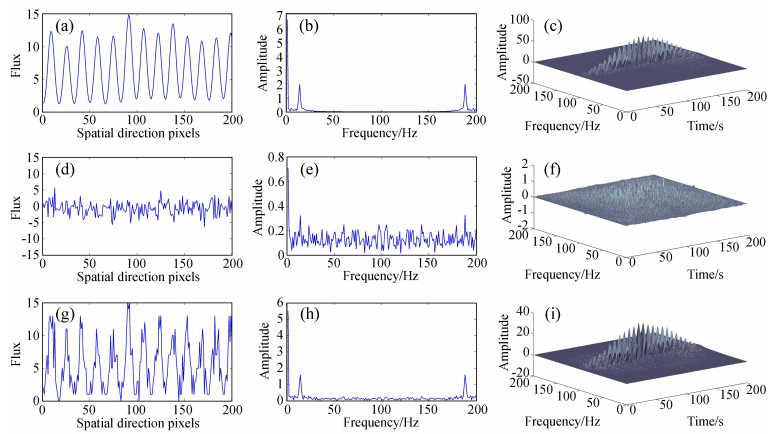
1 低信噪比信号的时频特性光纤光谱信号在空间方向的分布类似于高斯分布,其中参杂的主要是泊松噪声[6],在高信噪比条件下,信号波形光滑而规则,在低信噪比时,信号波形杂乱无序,如图 1(a)、 (d)、 (g)。在傅里叶变换域,光谱信号的能量主要集中在低频带,噪声能量分散在整个频带,且二者存在交叉混叠,如图 1(b)、 (e)、 (h)。空间方向的一维光纤光谱信号可以表示为
| x(n)=s(n)+ε(n) | (1) |
|
| 图 1 (a) 参考信号波形图; (b) 参考信号的快速傅里叶变换频谱图; (c) 参考信号的Wigner分布图; (d) 噪声波形图; (e) 噪声的快速傅里叶变换频谱图; (f) 噪声的Wigner分布图; (g) 低信噪比信号波形图; (h) 低信噪比信号的快速傅里叶变换频谱图; (i) 低信噪比信号的Wigner分布图 Fig. 1 1An example of signal filtering. (a) The waveform of a sequence of reference signals; (b) The FFT spectrum of the reference signals; (c) The amplitiudes of Wigner components of the reference signals; (d) The waveform of certain noise; (e) The FFT spectrum of the noise; (f) The amplitudes of Wigner components of the noise; (g) The waveform of the low-SNR data consisting of the reference signals and the noise; (h) The FFT spectrum of the low-SNR data; (i) The amplitudes of Wigner components of the low-SNR data |
x(n)为低信噪比的观测信号;s(n)为纯净的有效信号;ε(n)为噪声。
文[3]将Winger变换方法引入光谱信号的降噪,离散信号x(n)的Wigner变换[7]的定义为
| ${W_x}\left( {n,k} \right) = 2\sum\limits_{m = - \infty }^\infty {x\left( {n + m} \right)} x*\left( {n - m} \right){e^{ - j2mk}}$ | (2) |
x*(n)是输入信号的复共轭。加窗的离散Wigner分布可以表示为
| ${W_x}\left( {n,k} \right) = 2\sum\limits_{m = - L}^L {w\left( m \right)w} *\left( { - m} \right)x\left( {n + m} \right)x*\left( {n - m} \right){e^{ - j\frac{{4\pi mk}}{N}}}$ | (3) |
w(m)为窗函数;N=2L+1为输入信号长度。对有限长一维光谱信号计算Wigner分布时,可以认为所加窗为单位矩形窗函数,即w(m)=1,窗长为N,则得到的Wigner变换矩阵尺寸为N × N。
Wigner变换可以看作输入信号的自相关函数的傅里叶变换,同时描述了信号在时间域和频率域的特性,具有很高的时频分辨率。用高信噪比的平场信号(与目标光谱具有相似的点扩展函数和形状)作为参考,图 1(c)、 (f)、 (i)画出了干净的参考信号、噪声和含噪信号的Wigner分布函数(为了分析方便,将频谱图进行反转,使能量集中在中心位置),可以看出,信号在Wigner时频域分布更集中,能量峰值更明显,这有利于提取有效光谱信息,而噪声能量较分散地分布在整个时频面上,所以简单地通过选取截止频率的低通滤波器不能实现降噪的目标。
2 滤波方法设计针对传统时频滤波方法[3, 5]没有考虑混叠噪声的影响,采用Wigner变换获得光谱信号的时频分布,根据信号能量和噪声能量的分布差异,先设计带通滤波器滤除明显的噪声成分,再在信号和噪声的混叠区域,设计基于先验信噪比的加权滤波器进行处理,有效抑制混叠噪声的影响。
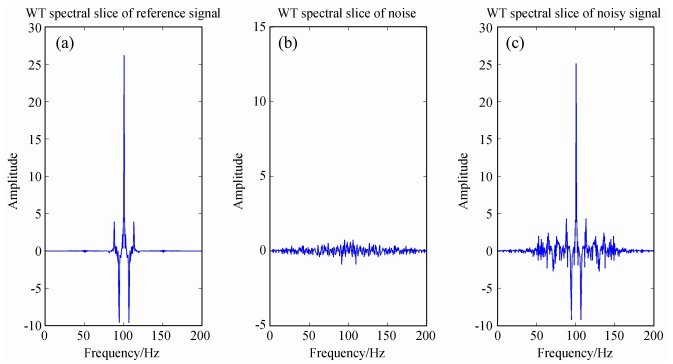
固定Wigner分布函数的时间域分量,获取光谱信号的Wigner频谱切片数据,以便于比较分析。图 2为时间分量n=100时,参考信号、噪声以及低信噪比信号的WT分布函数的频谱切片图。由图 2可以看出,WT分布使信号能量更集中(主要在中心峰和两个负的侧峰上),而噪声分散在整个域上;对比(a)、 (b)可知,在信号频谱峰值处,信噪比最大,有效信号成分最多;对比(a)、 (c)可知,噪声的存在使得能量有所发散,信号谱峰之间存在混叠噪声。因此,可以设计这样的滤波器:先设计带通滤波器,寻找合适的截止频率,滤除较分散的噪声能量。再对通带内的信号,估计其先验信噪比,在信噪比高的位置,有效信号成分多,赋予大的权值,使频谱峰值更尖锐;信噪比低的位置,噪声成分多,赋予小的权值,抑制噪声。
|
| 图 2 信号的WT分布函数频谱切片图(时间分量n=100). (a) 参考信号的WT频谱切片; (b) 噪声的WT频谱切片; (c) 低信噪比信号的WT频谱切片 Fig. 2 Comparison of Wigner Transformation (WT) spectral slices of the reference signals, the noise, and the low-SNR data shown in Fig.1. Each slice is of the component of n=100. The panels (a), (b), and (c) are the slices of the reference signals, the noise, and the low-SNR data, respectively |
初始滤波:截止频率的选取对于降噪效果有很大影响,在尽可能滤除噪声的同时需保证有效信号能量不被破坏。由于谱图对称,可参考文[3]的思想,从频谱切片图的两边同时向中间对像素点幅值叠加求和,找到叠加之和恰好等于所有像素点幅值总和的0.2%时对应的两点位置ω1、ω2作为第1、2个截止频率,再继续向中间求和,在叠加之和恰好等于所有像素点幅值总和的0.4%对应的两点位置ω3、ω4作为第3、4个截止频率,在通带和阻带之间产生一个过渡带,设计n时刻的滤波器如下:
| ${H_1}\left( {n,k} \right) = \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k \le {\omega _1}\;\;{\rm{or}}\;\;k \ge {\omega _2}\\ 2{\left[{\left( {k - {\omega _1}} \right)/\left( {{\omega _3} - {\omega _1}} \right)} \right]^2}\;\;\;\;\;\;\;{\omega _1} \le k \le \left( {{\omega _1} + {\omega _3}} \right)/2\\ 1 - 2{\left[{\left( {k - {\omega _3}} \right)/\left( {{\omega _3} - {\omega _1}} \right)} \right]^2}\;\;\;\left( {{\omega _1} + {\omega _3}} \right)/2 \le k \le {\omega _3}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _3} \le k \le {\omega _4}\\ 1 - 2{\left[{\left( {k - {\omega _4}} \right)/\left( {{\omega _2} - {\omega _4}} \right)} \right]^2}\;\;\;{\omega _4} \le k \le \left( {{\omega _4} + {\omega _2}} \right)/2\\ 2{\left[{\left( {k - {\omega _2}} \right)/\left( {{\omega _2} - {\omega _4}} \right)} \right]^2}\;\;\;\;\;\;\;\;\left( {{\omega _4} + {\omega _2}} \right)/2 \le k \le {\omega _2} \end{array} \right.$ | (4) |
加权滤波:由图 2的分析可知,噪声在整个频带内近似均匀分布,可以由阻带部分的噪声时频点值Wx(n,k)估计每个时刻n的噪声平均分量D(n)=E(Wx(n,k)),k=ω2,…,N,用来近似通带内的噪声平均分量。在通带部分,频谱峰值处信噪比很高,实际处理时,峰值处的信号能量近似等于有效信号能量。所以,可以将频谱切片中减去噪声平均分量的各时频点值与频谱峰值进行对比,用以设计滤波函数。若比值较大,说明有效信号成分多,应赋给对应时频点较大的权值;若比值较小,说明噪声成分多,应赋给对应时频点较小的权值。由于两侧峰值和中心峰值差距较大,所以进行分段设计,先找到n时刻的频谱切片的3个谱峰(包括2个负峰值)位置对应的频率值μ1、μ2、μ3,结合带通滤波的截止频率ω1、ω2确定分段区间,则n时刻的滤波函数为
| ${\tilde H_2}\left( {n,k} \right) = 1 + \alpha \frac{{\left| {\left| {{W_x}\left( {n,k} \right)} \right| - D\left( n \right)} \right|}}{{\begin{array}{*{20}{c}} {\max }\\ {i \in {\Omega _j}} \end{array}\left| {{W_x}\left( {n,i} \right)} \right|}},k \in {\Omega _j},j = 1,2,3$ | (5) |
其中,${\Omega _1} = \left[{{\omega _1},\frac{{{\mu _1} + {\mu _2}}}{2}} \right],{\Omega _2} = \left[{\frac{{{\mu _1} + {\mu _2}}}{2} + 1,\frac{{{\mu _2} + {\mu _3}}}{2}} \right],{\Omega _3} = \left[{\frac{{{\mu _2} + {\mu _3}}}{2} + 1,{\omega _2}} \right]$为分段区间,$\begin{array}{*{20}{c}} {\max }\\ {i \in {\Omega _j}} \end{array}\left| {{W_x}\left( {n,i} \right)} \right|,j = 1,2,3$为沿频率轴方向取对应段的极大值,即频谱峰值,α∈(0,1)为可调参数,调整加权的程度。由于峰值处的信号能量近似看作有效信号能量,可将其权值设为1,滤波函数归一化为
| ${H_2}\left( {n,k} \right) = \frac{{{{\tilde H}_2}\left( {n,k} \right)}}{{\begin{array}{*{20}{c}} {\max }\\ {i \in {\Omega _j}} \end{array}{{\tilde H}_2}\left( {n,i} \right)}},k \in {\Omega _j}j = 1,2,3$ | (6) |
同样方法得到所有时刻n(n=1,…,N)的滤波函数。图 3为加权滤波器H2的切片图(n=100),可以看到,信号的每个时频点有不同的权值。

|
| 图 3 加权滤波器的切片图(n=100) Fig. 3 A plot of the weighted-filter slice of n=100 |
经过两步滤波,获得有效信号的时频分布函数${W_{\hat s}}\left( {n,k} \right)$。由于光纤光谱信号非负,根据WT的边缘特性,对于特定时刻n,${W_{\hat s}}\left( {n,k} \right)$沿全频轴的积分等于此时刻信号的瞬时功率${\left| {\hat s\left( n \right)} \right|^2}$,可重构信号${\hat s\left( n \right)}$,2L+1=N为数据总长(以下取N=201)。
| $\hat s\left( n \right) = \sqrt {\frac{1}{{2L + 1}}\sum\limits_{k = - L}^L {{W_{\hat s}}\left( {n,k} \right)} } $ | (7) |
对于图 2(c)的低信噪比信号的WT频谱切片,
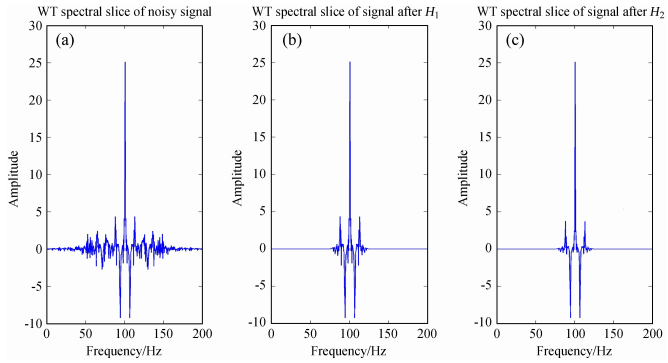
经过H1和H2滤波的结果如图 4(b)和图 5(c)。可以看出,H1滤波后的谱峰两侧的噪声被明显滤除,H2滤波后谱峰之间的混叠噪声被抑制,谱峰值更加尖锐。
|
| 图 4 WT分布频谱切片图(n=100). (a) 低信噪比信号的WT频谱切片; (b) 经过H1滤波后信号的WT频谱切片; (c) 经过H2滤波后信号的WT频谱切片 Fig. 4 Plots of WT spectral slices of the low-SNR data at different processing stages. Each slice is for the component of n=100. The panels (a), (b), and (c) are for slices before processing, after H1 filtering, and after H2 filtering, respectively |

|
| 图 5 模拟数据的降噪对比图. (a) 低信噪比信号; (b) 对应参考信号; (c) 改进算法的结果; (d) 传统WT结果; (e) 快速傅里叶变换的结果 Fig. 5 Plots of results of denoising simulated low-SNR data. (a) The plot of the simulated low-SNR data before denoising; (b) The plot of the reference signals in the data; (c) The plot of results of our improved method; (d) The plot of results of the conventional WT; (e) The plot of results of the FFT |
为验证加权滤波方法对低信噪比光纤光谱信号的降噪效果,使用输出信噪比($SNR = 10\;{\log _{10}}\left( {\sum\limits_{i = 1}^N {{{\hat s}^2}\left( i \right)/\sum\limits_{i = 1}^N {{{\left( {x\left( i \right) - \hat s\left( i \right)} \right)}^2}} } } \right)$),皮尔森相关系数[8]和方差3个指标。信噪比用于描述恢复信号的降噪程度,皮尔森相关系数用于描述恢复信号与原始参考信号的相似程度,方差用于描述恢复信号与原始参考信号的偏差。
模拟数据根据LAMOST望远镜系统的相关技术参数仿真生成,最大半峰宽(FWHM)约为8个像素。两个相邻光纤的中心间距约为14至16个像素。模拟噪声是能量很强的泊松噪声,实验数据的输入信噪比为7.5 dB~8.9 dB。
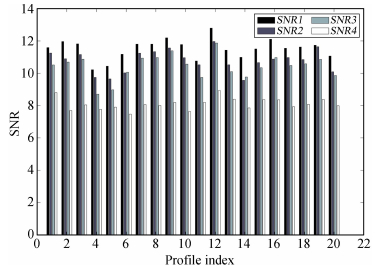
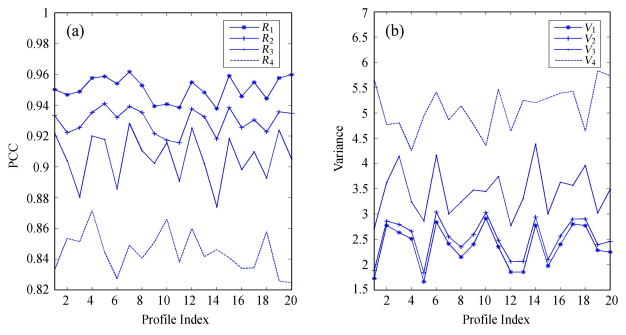
经过多次实验,选定α=0.6作为加权系数,并采用快速傅里叶算法[4]和传统WT算法[6]作为对比。如图 5,和快速傅里叶算法以及WT算法相比,本文的算法能抑制更多的随机噪声,并且恢复的波形更平滑,和参考信号更接近。图 6列出了20组实验的恢复信号的信噪比,由图可知,3种降噪方法都能使输出信噪比大于输入信噪比,但是基于加权滤波方法的输出信噪比比其他两种方法提高得更多。图 7列出了20组实验结果的皮尔森相关系数和方差。结果表明,改进算法具有更大的皮尔森相关系数和更小的方差,因此比传统Winger变换算法和快速傅里叶变换算法具有更好的滤波结果。
|
| 图 6 信噪比对比图。SNR1为改进算法的输出信噪比,SNR2为WT算法的结果,SNR3为快速傅里叶算法的结果,SNR4为输入信噪比 Fig. 6 Comparison of signal-to-noise ratios of the simulated low-SNR data after being denoised by different methods. The SNR1, SNR2, SNR3, and SNR4 denote the results of our improved method, the conventional WT, the FFT, and without denoising, respectively |
|
| 图 7 实验评估参数对比图. (a) 皮尔森相关系数 (PCC); (b) 方差。R1、V1为改进算法和参考信号的PCC和方差,R2、V2为WT算法的结果,R3、V3为快速傅里叶算法结果,R4、V4为带噪信号和参考信号的结果 Fig. 7 Comparison of evaluation-parameter values for the results of denoising the simulated low-SNR data using different methods. (a) Comparison of Pearson Correlation Coefficient (PCC) values. The PCC here is that between the result data and the reference signals; (b) Comparison of the variances. In the panels, R1 and V1 denote the results of our improved method; R2 and V2 denote the results of the conventional WT; R3 and V3 denote the results of the FFT; R4 and V4 denote the values for data before denoising |
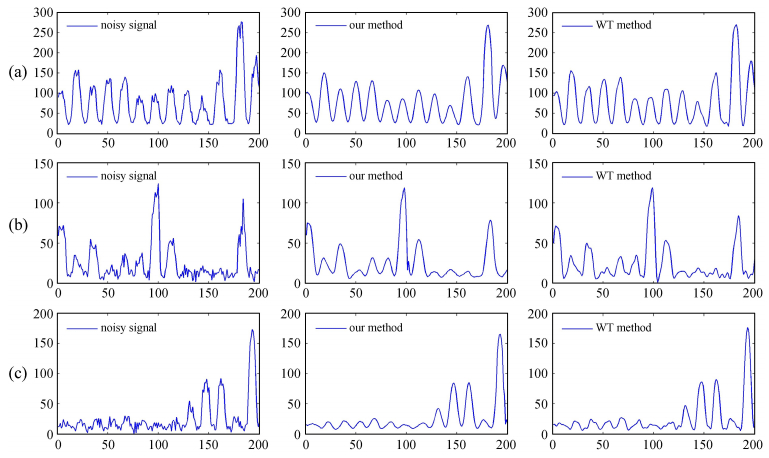
为了测试所提算法在实际天文观测信号中的有效性,对LAMOST望远镜系统的实测数据进行实验。选取目标天体星等很高的暗弱星体的观测信号作为实验数据,因此满足低信噪比条件。数据编号为ro-04r-20100121(MJD=79514244)和ro-13b-20100121(MJD=79514169)。一幅完整的二维光纤光谱实测图像尺寸为4136 × 4160,实验时,每组选取201个像素点长度。图 8可以看出,改进方法和传统Wigner变换方法均能移除存在于光谱信号中的随机噪声,但本文的方法恢复的信号波形更加平滑,波形特征更明显,为后续的高精度的光谱抽取处理创造了条件。
|
| 图 8 3组基于LAMOST实测数据的降噪结果对比图(x坐标为像素点, y坐标为流量值). (a) ro-04r-20100121 (MJD=79514244), Domain (2500, 700∶899); (b) ro-13b-20100121 (MJD=79514169), Domain (3600,710∶909); (c) ro-13b-20100121 (MJD=79514169), Domain (3450,1300∶1499) 在(a)(b)(c)中,从左到右依次为:低信噪比信号,改进算法的结果,传统WT的结果 Fig. 8 Comparison of denoising results of different methods applied to three sets of data observed with the LAMOST. The x axis is for pixel positions, and the y axis is for fluxes. (a) Comparison using the data of ro-04r-20100121 (MJD=79514244) within the Domain (2500, 700∶899); (b) Comparison using the data of ro-13b-20100121 (MJD=79514169) within the Domain (3600, 710∶909); (c) Comparison using the data of ro-13b-20100121 (MJD=79514169) within the Domain (3450,1300∶1499). In the comparison with each set, from the left to the right, the three panels are for the data without denoising, the results of our improved method, and the results of the conventional WT, respectively |
针对低信噪比条件下光谱抽取精度较低的问题,对输入二维光谱图像进行预处理。通过分析低信噪比光纤光谱信号在空间方向的时频特性,针对传统低通滤波不能滤除混叠噪声的缺陷,将Wigner变换应用于光谱信号的时频分析,提出基于先验信噪比的加权滤波新思路:先用带通滤波器进行初始滤波,滤除明显的较分散的噪声分量,再在通带内设计信噪比加权滤波器,根据有效信号成分和噪声成分的比例进行非线性处理,保持有效信号成分,抑制混叠的噪声分量,最后利用Wigner变换的边缘特性重构有效信号。实验部分采用输出信噪比、皮尔森相关系数和方差作为评价指标。基于LAMOST系统的模拟和观测数据的实验结果表明所提算法的有效性,与传统的快速傅里叶变换和Wigner变换算法相比,改进算法在抑制噪声和波形保持方面效果更好,有利于后续进行高精度的光谱能量抽取处理。
| [1] | Cui Xiangqun, Su Dingqiang, Wang Yanan, et al. The optical performance of LAMOST telescope[C]//Proceedings of the SPIE. 2010. |
| [2] | Rhoads J E. Cosmic-ray rejection by linear filtering of single images[J]. Publications of the Astronomical Society of the Pacific, 2000, 112(771): 703-710. |
| [3] | 崔波, 叶中付, 白仲瑞. LAMOST二维光纤光谱抽谱方法的研究[J]. 天文学报, 2008, 49(3): 327-338. Cui Bo, Ye Zhongfu, Bai Zhongrui. The extraction algorithm for LAMOST two-dimensional spectrum image[J]. Acta Astronomica Sinica, 2008, 49(3): 327-338. |
| [4] | Zhu Z Q, Wang C, Ye Z F. Pretreatment for 2D astronomical spectrum images with low S/N before the spectra extracting[J]. Publications of the Astronomical Society of the Pacific, 2009, 121(875): 54-58. |
| [5] | Zhu J, Zhu Z Q, Ye Z F. Profile detection for astronomical spectrum data with low SNR via the Wigner transform[C]//2011 International Conference on Multimedia and Signal Processing (CMSP). 2011: 324-328. |
| [6] | Pych W. A fast algorithm for cosmic-ray removal from single images[J]. Publications of the Astronomical Society of the Pacific, 2004, 116(816): 148-153. |
| [7] | Claasen T A C M, Mecklenbrauker W F G. The Wigner distribution: a tool for time-frequency signal analysis-part 2: discrete time signal[J]. Philips Journal of Research, 1980, 35: 276-300. |
| [8] | Benesty J, Chen J, Huang Y A. On the importance of the pearson correlation coefficient in noise reduction[J]. IEEE Transactions on Audio Speech and Language Processing, 2008, 16(4): 757-765. |



