2. 国防科技大学电子科学与工程学院电子工程所, 湖南长沙 410073
2. Research Institution of Electronic Engineering, School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China
在地球表面可以实现观测的10 MHz~300 GHz频段内,射电天文学家几乎对这频段的所有频率感兴趣[1],而全球性卫星导航系统占用了L波段在1.1 GHz~1.6 GHz之间约150 M的带宽,严重限制了射电天文在该频段的观测,降低了大型射电科学仪器的使用价值。射电天文观测被动接收来自宇宙中射电源所辐射的极其微弱的射电信号,很容易受到有源电磁业务活动的影响。因此射频干扰的消除俨然已成为新一代射电望远镜需要克服的主要障碍和亟待解决的突出问题。对于选址较好的射电天文望远镜而言较难受到地面的电磁干扰,但是来自卫星导航信号的干扰却不可避免。
为了抑制和消除射电望远镜观测21 cm谱线[2, 3, 4]红移过程中出现的导航卫星信号干扰,本文将雷达、通信等领域的微弱信号处理方法与射电天文信号自身的特点相结合,设计了一种自适应滤波方案。本方案是借助辅助天线所接收的卫星导航信号,利用最小均方误差自适应滤波方法将望远镜观测数据中的卫星导航干扰信号消除。
最小均方误差自适应算法由于计算量小、结构简单、易于实现实时处理,因此在噪声对消、谱线增强、系统识别以及干扰消除等诸多领域得到了广泛应用。众所周知,稳态误差直接与步长成比例,然而步长减小,算法收敛时间增加。变步长最小均方误差算法的提出为解决稳态误差和收敛速度之间的矛盾开辟了一条有效的途径。目前发展了一系列变步长自适应算法,有的算法[5, 6]通过对前刻步长的修改得到当前步长;有的算法[7, 8]则是通过非线性函数来调整步长。本文在研究文[8]所述的一类变步长最小均方误差算法的基础上,提出了一种新的变步长最小均方误差算法。
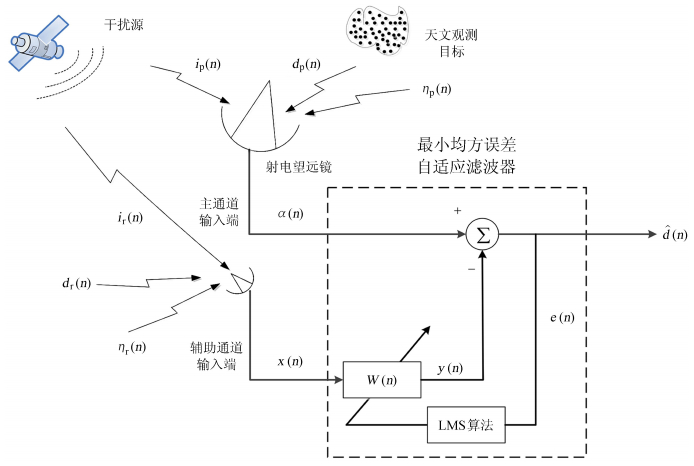
1 接收信号模型随着微弱信号处理技术的发展,自适应信号处理已经在诸如雷达、通信、声纳及地震探测等领域得到越来越广泛的应用[9, 10],结合射电天文信号的特点,将其应用于射电天文领域的射频干扰消除。如图 1,将最小均方误差自适应干扰消除系统应用于射电天文望远镜观测中。射电望远镜(主天线)接收的信号中不仅仅含有由射电源辐射进入天线主瓣的天文目标信号dp(n),还包含由天线旁瓣进入的干扰信号ip(n)以及白噪声ηp(n),其中ηp(n)包含背景噪声、接收机热噪声、宇宙噪声以及天线的溢出噪声等。因此可以得到主天线馈源处的信号α(n),它是以上3种信号之和,即
| α(n)=dp(n)+ip(n)+ηp(n). | (1) |
|
| 图 1 最小均方误差自适应滤波器在射电天文干扰消除中的应用 Fig. 1 Illustration of application of an LMS adaptive filter in reducing interferences in radio astronomy |
对于辅助天线而言,虽然它是对准干扰源进行接收的,即辅助天线在干扰方向上较主天线具有更高的天线增益,则在辅助通道输入端的信号x(n)较α(n)具有更高的干噪比,但仍会有少量的天文信号进入,即
| x(n)=ir(n)+dr(n)+ηr(n), | (2) |
式中,下标p和r分别表示主天线和辅助天线。
通过不断地调整滤波器权值矢量W(n)的值,使得辅助通道输出的干扰逐渐逼近主通道中的干扰信号。滤波器输出量y(n)中,包含对主通道干扰信号的估计${\hat i_p}\left[n \right]$和噪声ηh[n],其中ηh[n]是ηr[n]经W(n)处理后的有色噪声。因此,y(n)可以表达为
| $y\left( n \right) = {W^T}\left( n \right)X\left( n \right) = {\hat i_p}\left( n \right) + {\eta _h}\left( n \right)$ | (3) |
其中,X(n)=x(n)x(n-1)…x(n-M+1)T为辅助通道输入信号序列;M为滤波器阶数;W(n)=[w0(n)w1(n)…wM-1(n)]T为自适应滤波器的加权系数。
由于辅助通道端的干扰信号ir(n)与主通道端的干扰信号ip(n)存在某些相关性,所以采用自适应滤波器的主要目的就是把这种相关性表示为以时间为自变量的函数。自适应算法的作用是通过比较先前和目前的信息,把更新后的加权系数发送给数字滤波器,然后数字滤波器再通过不断地调整权值矢量的值,使得辅助通道输出的干扰${\hat i_p}\left( n \right)$逐渐逼近主通道中的干扰信号ip(n)。
2 最小均方误差算法的改进与分析 2.1 传统最小均方误差算法首先,简要介绍一下传统的固定步长最小均方误差算法。如图 1,固定步长最小均方误差自适应算法的迭代公式为
| e(n)=α(n)-y(n), | (4) |
| y(n)=WT(n)X(n), | (5) |
| W(n+1)=W(n)+2μX(n)e*(n), | (6) |
| 0<μ<1/λmax, | (7) |
其中,α(n)为主通道输出信号;e(n)为误差信号;μ为步长。(7)式给出了确保自适应滤波算法收敛的条件,其中1/λmax为辅助通道输入信号自相关矩阵的最大特征值。
对于固定步长的最小均方误差算法而言,其在收敛速度与稳态失调之间对步长的选取是矛盾的,为解决这一矛盾,对最小均方误差中的固定步长加以改进缩短其收敛过程,归一化最小均方算法就是其中一种基本的方法。此类算法可描述如下:
| e(n)=α(n)-WT(n)X(n), | (8) |
| $W\left( {n + 1} \right) = W\left( n \right) + \frac{\mu }{{{{\left\| {X\left( n \right)} \right\|}^2}}}X\left( n \right)e*\left( n \right)$ | (9) |
其中,‖ ‖表示求欧式范数运算。
最后,介绍一下文[8]提出的一类变步长算法VS-NNMS,此类算法的迭代公式为
| e(n)=α(n)-WT(n)X(n), | (10) |
| μV(n)=λ2[1-exp(-λ1丨e(n)丨2)], | (11) |
| W(n+1)=W(n)+μV(n)X(n)e*(n), | (12) |
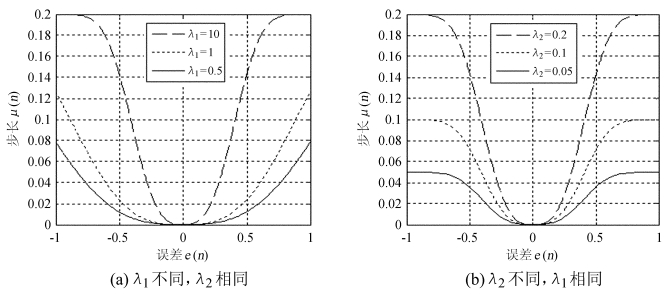
其中,μV(n)为变步长最小均方误差算法的步长;系数λ1、λ2为取值与e(n)无关的常值参数,且均大于0。图 2为变步长μV(n)与误差e(n的函数关系曲线。
|
| 图 2 步长与误差的关系曲线 Fig. 2 Dependencies of signal errors on step-size values for fixed λ2 and fixed λ1, respectively, in the VS-NNMS algorithm |
由图 2可知,此类变步长算法的优点是,在初始收敛阶段步长具有较大取值,从而有较大的收敛速度;而在算法收敛后,则保持较小的步长取值,从而获得很小的稳态误差。但从图中也可以发现:当误差在接近0点处变化时,即算法已达到或将要达到稳态时,步长随误差变化较快,不具有缓慢变化的特性,使得算法在稳态阶段仍有较大的步长变化,由此导致算法稳定后仍有较大的稳态误差。
2.2 改进的变步长最小均方误差算法及分析考虑到上述变步长算法当误差e(n在0处附近取值时,步长μV(n)变化太快。为此,本文通过求平均和引入变化因子$\sqrt {\left| {e\left( n \right)} \right|} $改变步长随误差变化的函数关系曲线形状,使得改进后的步长μG(n)在e(n0点附近具有缓慢变化的特性。令新的步长${\mu _G}\left( n \right) = \frac{{{\mu _V}\left( n \right) + {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( n \right)} \right|} $,则得到改进后算法步长的变化量ΔμG(n)为
| $\begin{array}{l} {\mu _G}\left( n \right) = \frac{{{\mu _V}\left( n \right) + {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( n \right)} \right|} \\ \Delta {\mu _G}\left( n \right) = {\mu _G}\left( {n + 1} \right) - {\mu _G}\left( n \right)\\ = \frac{{{\mu _V}\left( {n + 1} \right) + {\mu _V}\left( n \right)}}{2}\sqrt {\left| {e\left( {n + 1} \right)} \right|} - \\ \frac{{{\mu _V}\left( n \right) + {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( n \right)} \right|} \end{array}$ | (13) |
在算法收敛的情况下有丨e(n+1)丨≤丨e(n)丨成立,所以可将上式简化为
| $\begin{array}{l} \Delta {\mu _G}\left( n \right) \le \frac{{{\mu _V}\left( {n + 1} \right) + {\mu _V}\left( n \right)}}{2}\sqrt {\left| {e\left( {n + 1} \right)} \right|} - \frac{{{\mu _V}\left( n \right) + {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( {n + 1} \right)} \right|} \\ = \frac{{\left( {{\mu _V}\left( {n + 1} \right) - {\mu _V}\left( n \right)} \right) + \left( {{\mu _V}\left( n \right) - {\mu _V}\left( {n - 1} \right)} \right)}}{2}\sqrt {\left| {e\left( {n + 1} \right)} \right|} \\ = \frac{{\Delta {\mu _V}\left( n \right) + \Delta {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( {n + 1} \right)} \right|} \end{array}$ | (14) |
又由对(11)式两边求二阶导数可得
| $\begin{array}{l} \frac{{{{\rm{d}}^2}{\mu _V}\left( n \right)}}{{{{\rm{d}}^2}{e^2}\left( n \right)}} = \frac{{{\rm{d}}\left\{ {2{\lambda _1}{\lambda _2}e\left( n \right)\exp \left[{ - {\lambda _1}{e^2}\left( n \right)} \right]} \right\}}}{{{\rm{d}}e\left( n \right)}}\\ = 2{\lambda _1}{\lambda _2}\left[{ - 2{\lambda _1}{e^2}\left( n \right)} \right]\exp \left[{ - {\lambda _1}{e^2}\left( n \right)} \right] \end{array}$ | (15) |
由于λ1和λ2均是大于0的参数,所以由上式可知,在e2(n)取值小于1/(2λ1)时,μV(n)的二阶导数取值大于0,而在e2(n)大于1/(2λ1)取值时,μV(n)的二阶导数小于0,即
| $\left\{ \begin{array}{l} \frac{{{{\rm{d}}^2}{\mu _V}\left( n \right)}}{{{{\rm{d}}^2}{e^2}\left( n \right)}} > 0,{\left| {e\left( n \right)} \right|^2} < 1/\left( {2{\lambda _1}} \right)\\ \frac{{{{\rm{d}}^2}{\mu _V}\left( n \right)}}{{{{\rm{d}}^2}{e^2}\left( n \right)}} < 0,{\left| {e\left( n \right)} \right|^2} > 1/\left( {2{\lambda _1}} \right) \end{array} \right.$ | (16) |
将其代入(14)式可得
| $\left\{ \begin{array}{l} \Delta {\mu _G}\left( n \right) < \Delta {\mu _V}\left( n \right)\sqrt {\left| {e\left( {n + 1} \right)} \right|} ,{\left| {e\left( n \right)} \right|^2} < 1/\left( {2{\lambda _1}} \right)\\ \Delta {\mu _G}\left( n \right) > \Delta {\mu _V}\left( n \right)\sqrt {\left| {e\left( {n + 1} \right)} \right|} ,{\left| {e\left( n \right)} \right|^2} > 1/\left( {2{\lambda _1}} \right) \end{array} \right.$ | (17) |
从上式可以看出,改进后算法的步长在稳态误差取值0(丨e(n)丨<1)附近时的变化要比改进前算法的步长变化缓慢。利用上面的公式分别画出改进前后算法的步长与稳态误差之间的关系曲线。
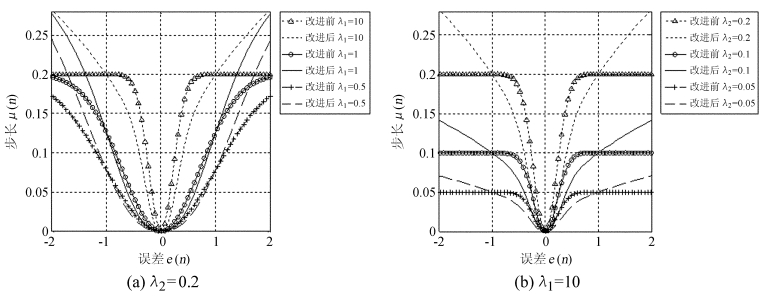
图 3(a)为固定λ2=0.2不变的情况下,不同λ1取值下的算法改进前后的步长与稳态误差e(n)之间的关系曲线。图 3(b)为固定λ1=10不变的情况下,不同λ2取值下的算法改进前后的步长与稳态误差e(n)之间的关系曲线。
|
| 图 3 改进后算法的步长和误差的关系图 Fig. 3 Dependencies of signal errors on step-size values for fixed λ2 and fixed λ1 , respectively, in our improved algorithm |
通过图 3可以看出,改进前后算法的步长与误差之间均存在非线性函数关系,随误差绝对值丨e(n)丨单调增加。算法参数λ1与λ2会影响函数关系曲线:随着λ1与λ2的增大,步长随丨e(n)丨的变化越陡峭;反之,随着λ1与λ2的减小,步长随丨e(n)丨的变化越缓慢。因此可知,在保证算法收敛的条件下,为了获得更快的收敛速度,应取较大的λ1与λ2值,使得步长较大;而当λ1取值趋近无穷大时,算法退化为上述固定步长的最小均方误差算法;而为了获得更小的算法稳态误差,应取较小的λ1与λ2值,使得步长变化缓慢。对比算法改进前后的关系曲线可知,改进后的算法通过引入求平均运算和变化因子√丨e(n)丨,能较好地改善函数形状,即在系统的初始阶段,步长取值增大,使得所对应的收敛速度更快,且随着收敛的加深,算法曲线底部的变化趋势变得更加缓慢,使得产生的稳态误差降低。
由前面介绍可知,改进后算法的步长μG(n)表达式为
| $\begin{array}{l} {\mu _G}\left( n \right) = \frac{{{\mu _V}\left( n \right) + {\mu _V}\left( {n - 1} \right)}}{2}\sqrt {\left| {e\left( n \right)} \right|} \\ = {\lambda _2}\left[{1 - \frac{1}{2}\exp \left( { - {\lambda _1}{{\left| {e\left( n \right)} \right|}^2}} \right) - \frac{1}{2}\exp \left( { - {\lambda _1}{{\left| {e\left( {n - 1} \right)} \right|}^2}} \right)} \right]\sqrt {\left| {e\left( n \right)} \right|} \end{array}$ | (18) |
由上式可知,改进后算法的步长μG(n)主要由算法参数λ1和λ2控制。
下面通过仿真实验分析并检验改进后变步长算法的收敛性能,采用的仿真条件为:自适应滤波器的阶数M=2;主通道输入的干扰是均值为0、方差为1的高斯白噪声信号,输入的噪声是均值为0、方差为0.04的高斯白噪声信号,且干扰与噪声之间不相关;辅助通道中输入的干扰是主通道干扰经FIR滤波器后的输出信号,且FIR系数为[0.8,0.5]T。为得到改进后算法的学习曲线和滤波器抽头权值的收敛曲线,分别做1 000次蒙特卡洛仿真,观测采样点数为2 000,然后求其统计平均值。
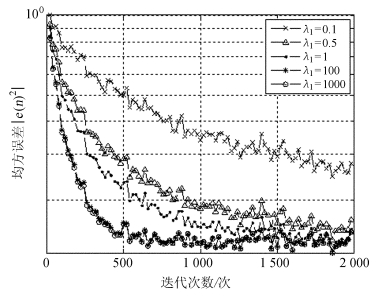
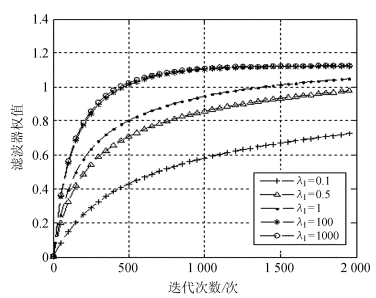
图 4和图 5分别为固定λ2=0.01,滤波器阶数取M=2时,不同λ1值所对应的算法均方误差和抽头权值的收敛关系曲线。
|
| 图 4 λ1值不同时的均方误差收敛曲线 Fig. 4 The convergence curves of mean square errors for different values of λ1 |
|
| 图 5 λ1值不同时的抽头权值收敛曲线 Fig. 5 The convergence curves of tap weights for different values of λ1 |
从关系曲线可以看出,在一定范围内,随着算法参数λ1的增大,算法的收敛速度逐步提高并且稳态误差失调量逐渐减小,而当λ1取值过大时将使得算法失去收敛性。
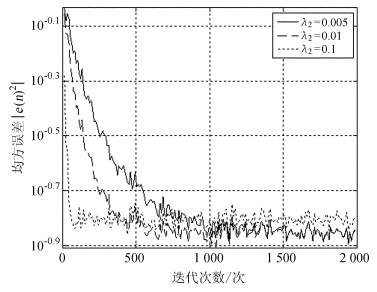
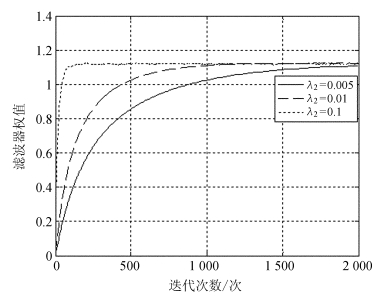
图 6和图 7分别为固定λ1=1 000,滤波器阶数取M=2时,不同λ2值所对应的算法均方误差和抽头权值的收敛关系曲线。
|
| 图 6 λ2值不同时的均方误差收敛曲线 Fig. 6 The convergence curves of mean square errors for different values of λ2 |
|
| 图 7 λ2值不同时的抽头权值收敛曲线 Fig. 7 The convergence curves of tap weights for different values of λ2 |
从关系曲线可以看出,在一定范围内,随着算法参数λ2的增大,算法的收敛速度逐步提高,而当λ2增大到一定程度之后,再随着λ2的增大,算法的收敛速度虽然加快,但同时稳态失调量也随着增加,以至于当λ2取值过大时导致算法发散。
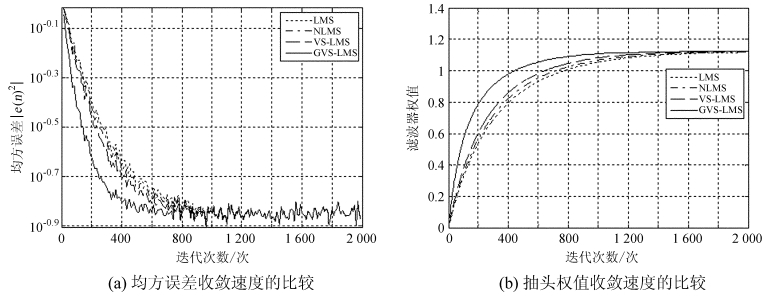
2.3 和其它最小均方误差算法的性能比较通过仿真实验对改进后的变步长算法与前面介绍的最小均方误差、归一化最小均方误差以及变步长最小均方误差算法进行比较,从仿真结果进一步说明改进后算法在性能上的改善。仿真条件与2.2节中的实验条件相同,分别做1 000次独立的仿真,然后求其统计平均值。图 8为改进后的变步长最小均方误差算法与其它3种算法在收敛速度上的比较。其中图 8(a)为在均方误差收敛速度上比较的结果,图 8(b)为在抽头权值收敛速度上比较的结果。
|
| 图 8 改进后算法与其它几种算法收敛速度的比较 Fig. 8 Comparison of convergence rates of our improved algorithm and other algorithms |
从图 8可以看出,在各算法达到相同稳态失调量的情况下,改进后的算法比其它几种算法具有更快的收敛速度。
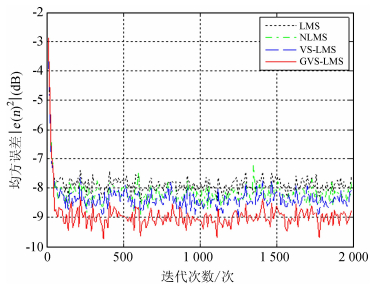
图 9是改进后的算法与其它3种算法在稳态失调量方面比较的结果。从图 9可以看出,在相同的收敛速度下,改进后的算法比其它几种算法具有更小的稳态失调量。
|
| 图 9 改进后算法与其它几种算法稳态失调量的比较 Fig. 9 Comparison of steady-state deviations of our improved algorithm and other algorithms |
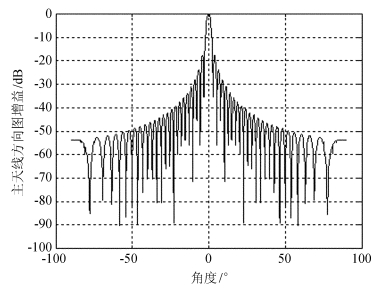
假设在某次21 cm谱线观测试验中,干扰信号从主天线的某个旁瓣方向进入,观测的带宽为20 MHz,中性氢红移后的中心频率为1 268.66 MHz(对应红移z=0.119 6),经下变频解调后的信号中心频率为16.50 MHz,即信号有效频率范围为6.50 MHz~26.50 MHz,功率通量密度约为1 mJy(1 Jy=10-26W/m2/Hz),并且天文信号的入射方向与望远镜视轴方向相同,即天文信号始终从主天线主瓣进入主天线。干扰源为 “北斗二号” B3频段的3号同步卫星,其信号中心频率为1.268 52 GHz,经下变频后干扰信号中心频率为16.36 MHz,其功率通量谱密度约为-210 dB(W/m2·Hz)。主天线口径为10 m、效率为0.72的抛物面天线,即有效面积为56 m2,方向图如图 10,半功率点波瓣宽度取值为1.7°,旁瓣电平取值为18 dB,热噪声温度为35 K。
|
| 图 10 主通道的归一化天线方向图 Fig. 10 The normalized antenna pattern of the primary channel |
辅助通道天线始终对准主天线旁瓣或远旁瓣进行接收,天线增益比主天线最大旁瓣增益高出5 dB,热噪声温度为110 K,所以依据上述条件可计算出当干扰信号从主天线旁瓣或远旁瓣入射主天线时,主通道观测数据干噪比为-40 dB,信噪比为-60 dB;辅助通道中观测数据的干噪比为2 dB,信噪比为-90 dB。
3.2 仿真结果(1)输出信干比
对于自适应抗干扰方法而言,输出天文信号dout可以表达为
| dout=dafterp(n)=dp(n)-dh(n) =dp(n)-WT(n)Dr(n), | (19) |
其中,Dr(n)[=dr(n)dr(n-1)…dr(n-M+1)]T表示辅助通道中天文信号的输入矢量。
残余干扰rfiout可表达为
| $\begin{array}{l} rf{i_{out}} = rfi_p^{after}\left( n \right)\\ = rf{i_p}\left( n \right) - r\hat f{i_p}\left( n \right)\\ = rf{i_p}\left( n \right) - {W^T}\left( n \right)RF{I_r}\left( n \right) \end{array}$ | (20) |
其中,RFIr(n)=[rfir(n)rfir(n-1)…rfir(n-M+1)]T表示辅助通道中干扰信号的输入矢量。
所以可得,经自适应抗干扰处理后的输出信干比SIRout为
| $\begin{array}{l} SI{R_{out}} = 10{\log _{10}}\frac{{{P_{{d_p}\left( n \right) - {W^T}\left( n \right){D_r}\left( n \right)}}}}{{{P_{fr{i_p}\left( n \right) - {W^T}\left( n \right)RF{I_r}\left( n \right)}}}}\\ = 10{\log _{10}}\frac{{1.1199 \times {{10}^{ - 20}}}}{{1.3643 \times {{10}^{ - 21}}}}\\ = 9.1428dB \end{array}$ | (21) |
由计算得到的输出信干比SIRout可知,利用自适应抗干扰方法对主通道中观测数据进行干扰信号消除时,可将输出信噪比提高到0 dB以上,在一定程度上降低了干扰信号对21 cm谱线弱信号检测的影响。
(2)残余干扰功率谱
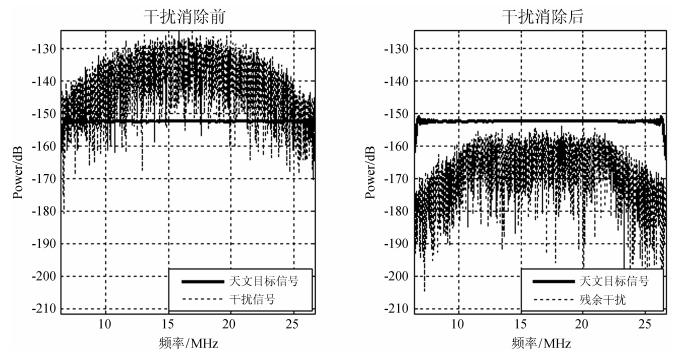
如图 11,给出了经自适应抗干扰处理后的残余干扰功率谱。由图 11可以明显看出,在进行抗干扰处理之前,天文目标信号的频谱完全被干扰所湮没,因此很难直接从观测数据中将21 cm红移信号检测出来。而通过利用自适应抗干扰方法将主通道观测数据进行干扰消除以后,可以发现在中性氢的各个红移观测频率上,残余干扰的功率均在天文信号功率以下,降低了干扰信号对21 cm观测的影响。
|
| 图 11 抗干扰前后干扰信号功率谱 Fig. 11 The power spectra of interference signals before and after cancellation of interferences |
(3)目标信号功率谱
对于自适应干扰消除方法而言,经抗干扰处理后,天文目标信号的变化量dh(n)为
dh(n)=dp(n)-dpafter(n),
其中,dp(n)表示干扰消除之前主通道观测数据中的天文目标信号;dpafter(n)表示干扰消除之后主通道观测数据中的天文信号。与求解残余干扰功率谱的方法类似,通过使用Bartlett法便可得到天文目标信号变化量dh(n)的功率谱为
${\hat D_h}\left( w \right) = \frac{1}{M}\sum\limits_{m = 0}^{M - 1} {\left| {\sum\limits_{n = 0}^{N - 1} {{d_h}\left( {n + mN} \right){e^{ - jnw}}} \left| {^2} \right.} \right.} ,\begin{array}{*{20}{c}} {n = 0,1,\ldots ,N - 1}\\ {m = 0,1,\ldots ,M - 1} \end{array}$
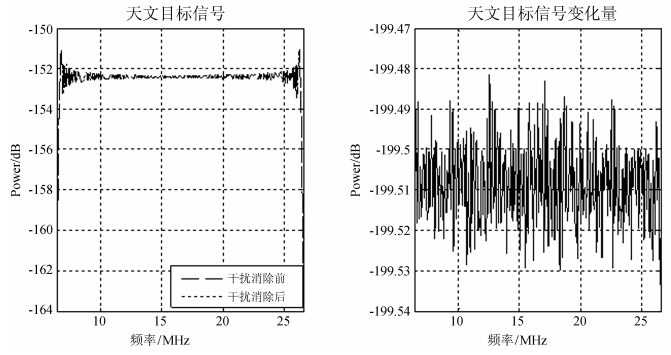
其中,N表示天文目标信号变化量每段数据的长度;M表示数据段的个数。并且可知,${\hat D_h}\left( w \right)$值越小,表明抗干扰处理对天文目标信号的影响就越小。如图 12为利用上式计算得到的目标信号功率谱:左图给出了自适应干扰消除前后的天文信号功率谱;右图给出了经自适应抗干扰处理引起的天文信号功率谱的变化量。
|
| 图 12 抗干扰前后天文目标信号功率谱 Fig. 12 The power spectra of astronomical-object signals before and after cancellation of interferences |
由图 12不难发现,经自适应抗干扰处理后的观测数据中,21 cm谱线信号的功率谱发生微小变化,这是抗干扰处理不想得到的结果,这种变化是由自适应干扰消除的本质引起的。自适应抗干扰方法通过借助主辅通道观测数据干扰信号之间的相关性,从而将主通道观测数据中的干扰信号消除。理想情况下,主辅两通道观测数据之间只存在干扰信号的相关,而在实际射电天文观测中,往往辅助天线不可避免地进入少量天文目标信号,这使得主辅通道观测数据之间的相关性不仅包含干扰信号间的相关,还存在天文信号间的相关,进而导致自适应抗干扰处理过程会造成主通道观测数据中天文目标信号发生改变。
4 结 论本文首先给出了射电天文观测背景下的自适应干扰消除原理,同时给出了该方法在射电系统下的接收信号模型,然后介绍了传统的3种最小均方误差自适应算法并分析了它们在弱信号干扰消除应用中存在的问题,随后对自适应算法的变步长加以改进,给出了算法参数的选取与算法性能之间的关系,并通过仿真实验对比分析了算法性能。最后通过仿真射电天文中21 cm谱线实验,利用改进后的自适应抗干扰算法进行干扰消除,结果表明:改进的最小均方误差自适应算法能够更好地解决自适应算法收敛速度与稳态误差之间的矛盾,在射电天文干扰消除中具有很好的干扰抑制和消除作用,并且干扰消除过程对天文信号的影响较小。
| [1] | 苗可可, 王壮, 程翥, 等. 高速同步数据采集系统性能测试方法研究[J]. 天文研究与技术——国家天文台台刊, 2014, 11(4): 417-422. Miao Keke, Wang Zhuang, Cheng Zhu, et al. A study of test methods for the performance of a high-speed synchronous data-acquisition system[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2014, 11(4): 417-422. |
| [2] | 陈学雷. 聆听天籁-暗能量测量与红移21 cm映射实验[C]//大口径射电望远镜关键技术和科学目标研讨会. 2010. |
| [3] | Chang T C, Pen U L, Bandura K, et al. An intensity map of hydrogen 21-cm emission at redshift z≈0.8 [J]. Nature, 2010, 466: 463-465. |
| [4] | 陈学雷. 暗能量的射电探测——天籁计划简介[J]. 中国科学:物理学 力学 天文学, 2011, 41(12): 1358-1366. Chen Xuelei. Radio detection of dark energy-the Tianlei projection[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2011, 41(12): 1358-1366. |
| [5] | Kwong R H, Johnston E W. A variable step size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992, 40: 1633-1642. |
| [6] | Mathews V J, Xie Z H. A stochastic gradient adaptive filters with gradient adaptive step sizes[A]. IEEE Transactions on Signal Processing, 1993, 41(6): 2075-2087. |
| [7] | Karni S, Zeng G. A new convergence factor for adaptive filters[J]. IEEE Transactions on Circuits and Systems, 1989, 36: 1011-1012. |
| [8] | 高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报, 2001, 29(8): 1094-1097. Gao Ying, Xie Shengli. A variable step size LMS adaptive filtering algorithm and its analysis[J]. Acta Electronica Sinica, 2001, 29(8): 1094-1097. |
| [9] | Manolakis D G, Ingle V K, Kogon S M. Statistical and adaptive signal processing: spectral estimation, signal modeling, adaptive filtering and array processing[M]. 北京: 电子工业出版社, 2002. |
| [10] | Haykin S. Adaptive filter theory [M]. 4th ed. Upper Saddle River: Prentice Hall, 2002. |


