近年来,随着科技的进步,无论是地面的还是天空的观测设备都在不断增加、改进和升级,各波段拥有各自优秀的望远镜建成并投入使用,如阿塔卡马大型毫米波/亚毫米波阵列(ALMA)[1]、澳大利亚平方千米阵列(ASKAP)[2]以及位于智利的光学观测设备Very Large Telescope(VLT)①(① http://www.eso.org/public/teles-instr/vlt/)等,随着观测能力越来越强,接收系统获得的数据量也越来越大,数据中包含的多维度信息也越来越丰富。
如何从“高维度”数据中完整展现所有的信息,对于天文这样一个以数据为基础的学科来说至关重要。利用数据可视化方法,可以发现数据背后的隐藏信息,还原和重构信息之间的相互关系,正如美国计算机科学家布鲁斯·麦考梅克在1987年关于科学可视化的定义②(② http://zh.wikipedia.org/zh-cn/%E7%A7%91%E5%AD%A6%E5%8F%AF%E8%A7%86%E5%8C%96)中阐述的,数据可视化能够“利用计算机图形学来创建视觉图像,帮助人们理解科学技术概念或结果的那些错综复杂而又往往规模庞大的数字表现形式”。对天文数据进行可视化有利于展示复杂天体如分子云、星系的结构,建立恒星形成、星系演化等模型,并且有助于对三维宇宙大尺度结构的研究。可以说,有效地展示多维度信息是天文研究的重要手段。
而目前的天文数据处理软件大多数没有完善的三维展示功能,对云、烟等无定形态物质和大规模粒子的三维模拟方法仍处在探索和发展中,部分天文软件采用利用二维图像加上一维谱线的方式体现三维特征,例如Starlink③(③ http://starlink.jach.hawaii.edu/starlink)软件包,或是按一定序列动态展示二维图像的方式显示三维特征,例如GIPSY④(④ http://www.astro.rug.nl/~gipsy/)等,但这些传统的二维图像显示模式已不能满足科学家们的需求,未来的天文研究需要更完善的数据展示方法和工具。
随着越来越多的科学家和团组意识到三维可视化对天文领域研究的重要性,并致力于开发满足宇宙及星系结构研究需求的三维可视化工具,可视化工具包的开发成为天文领域一个热门的研究方向,目前已经有一批软件被开发并且使用,例如美国国家射电天文台(National Radio Astronomy Observatory)开发的图像展示与分析工具CASA Viewer⑤(⑤ https://safe.nrao.edu/wiki/bin/view/Software/CasaViewer),小型科学家团队开发的用于光滑粒子流体动力学的光线跟踪算法Splotch⑥(⑥ http://www.mpa-garching.mpg.de/~kdolag/Splotch/),以及斯威本科技大学(Swinburne University of Technology)开发的三维可视化软件S2PLOT⑦(⑦ http://astronomy.swin.edu.au/s2plot/index.php?title=S2PLOT)等等,这些软件为相关领域的天文学家带来了便利。
与此同时,天文数据结构复杂、无定形态等特征,与其他领域的数据具有高度相似性,例如医学上展现组织结构的三维影像,地理上的等高线图等。由于有广泛的社会需求,这些领域已拥有比较成熟的三维展示软件,例如医学图像软件3Dslicer⑧(⑧ http://www.slicer.org/)。如果天文数据能转换成相应的格式,也可以使用这些软件研究天文领域的复杂图像如恒星形成区等[3]。
本文为天文学家介绍一款动画媒体领域使用的专业三维建模软件——Blender,及其在天文领域的优势和应用,并详细说明对三维数据单元和N体模拟数据的三维可视化工具的开发过程。
1 Blender简介本文使用的Blender[4]工具是一款支持高质量的建模、动画和渲染的开源三维建模软件,在GNU GLP的官方下载下支持Linux、Mac OS X、Windows操作系统平台,且在不同平台下界面保持一致。Blender内核由C语言写成,界面部分由C++写成,Python作为其应用程序编程接口(Application Programming Interface,API)及脚本编辑语言。为了方便用户进行更灵活的开发,Blender将用户界面(User Interface,UI)的开发代码封装到BPY库中,用户可以通过编写Python脚本自定义用户界面,并将自定义用户界面置于工具栏、属性栏等不同位置,还可以添加各种控件。
其灵活的图形界面,使得科学家在导入脚本后便可像使用一般软件那样利用Blender实现天文数据的可视化与简单分析,同时,Blender支持很多数据格式,包括静态图片常用的PNG、GIF、JPEG、TIF格式,动画的AVI、H.264、Quicktime、MPEG格式等,以及常用的三维模型文件格式,同时,Blender软件包含Python文本编辑器和命令行窗口,因此它能够方便地处理各种类型的天文数据例如FITS、HDF等,通过导入相应的Python科学扩展包也可以对数据进行快速读取和计算[5]。
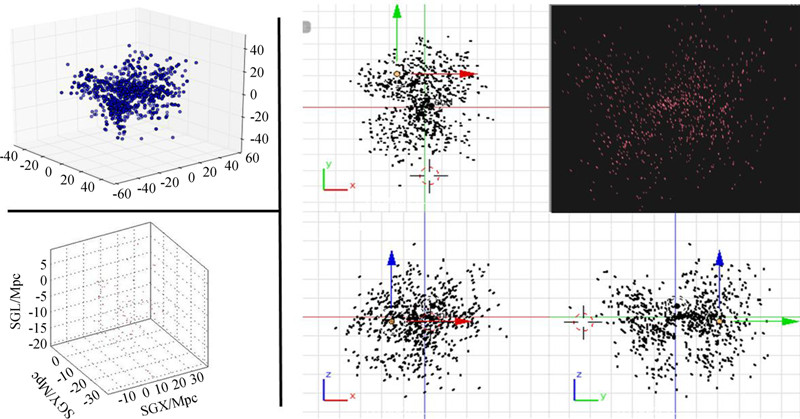
与普通三维建模软件相比,Blender具有跨平台性、用户界面可扩展性以及能够直接展示和处理天文数据的特点;与天文软件包相比,Blender具有更好的可视化效果,并能够实时地观察数据对象的三维结构,如图 1,分别展示了不同工具包对同一数据的三维可视化效果,数据源为范围z<=3 300 km/s邻近星系星表Cosmicflow-1 Distance[6]。
|
| 图 1 比较Blender与普通软件的可视化效果。左上图为利用Python自带的绘图库Matplotlib对数据的三维可视化,左下为用IDL绘制的结果,右侧为Blender的四视图效果和渲染结果 Fig. 1 Comparison between the visualization results of the Blender and commonly used software packages. The upper-left panel shows the results of the Matplotlib,which is the built-in plotting library of the Python package. The lower-left panel shows the results of using the IDL. The four panels in the middle and right constitute a set of four-view display rendered using the Blender |
从图 1可以看到,Blender可以实时地从不同角度对一个数据源的形态结构进行观察,自由灵活地调整视角,并且数据展示的清晰度更高,结构特征表现得更为明显,用户还可以通过材质纹理等个性化设置将数据模型渲染成高分辨率彩色图像,将研究成果更好地展现给公众。
由于对不同的数据结构处理需要使用不同的Python扩展包,重新编写程序,因此为了节约时间,方便进一步分析,在Blender环境下开发了对特定结构数据三维数据单元和N体模拟结果进行三维可视化的工具包。
2 基于Blender开发三维三维数据单元的可视化工具谱线三维数据单元在射电天文观测中有着广泛的运用,大多数中性氢、CO等数据结构均为三维数据单元,它由两个空间维度(通常是RA和Dec)、一个频率或波长维度以及通量值构成,通常的天文处理软件只是根据频率或波长谱线展现相应的二维图像及其每一点的通量谱线,对于三维数据单元的整体结构并没有一个完整展示。而在研究中,不仅应该考虑单独分子云的特征,更应该把握其形态结构和动力学结构,估计周围物质对它的影响,才可以更好地研究其形成和演化规律。因此,对三维数据单元的三维可视化能够更好地了解它的动态结构,为研究恒星形成和星系演化做准备,甚至可以在宇宙大尺度结构的研究上做一些科学推测。
下面以FCRAO 14 m望远镜对G25.4-0.14分子云[7]的CO谱线观测数据为例展示基于Blender开发的三维可视化插件工具。示例数据是一个三维数据单元,其文件为标准FITS格式,包含头文件和图像数据两部分,在头文件中用键值对的方式存储了文件基本信息以及与观测、定标有关的一些信息,图像数据部分为三维数组结构,每个数组元素存储了当前位置的源的通量值,对应银道面坐标银经范围是25.20°~26.00°、银纬范围是-0.504°~0.117°,径向速度范围是90.476~105.354 km/s,根据以下公式计算出分子云中心位置距离太阳为约5.7 kpc。
νr=νcosα-νsunsinl,
(1)
R2=Rsun2+d2-2Rsundcosl,
(2)
工具包的设计思路参考了开源工具包FRELLED⑨(⑨ http://www.rhysy.net/frelled.html),使用体绘制技术展示三维数据单元,并将整个可视化工具分为三大模块,分别为数据预处理模块、三维模型重建模块和数据分析模块,每一个模块有一个用户界面面板和相应的一系列控件实现用户交互,这三大功能模块的具体实现方法将分别在2.1、2.2和2.3节进行阐述,2.4节对当前工作进行总结。
2.1 数据预处理对标准FITS格式的谱线数据进行坐标转换、图像提取等操作,为后续的三维建模和数据分析模块做准备,预处理过程主要分为以下三个步骤:
(1)通过Python的PYFITS扩展库读取FITS文件的头信息中的关键字值和数据部分内容,对应关键字含义可参考FITS格式说明文档[8]。
(2)根据变量naxes的值,对使用了齐次坐标的数据集进行格式转换,将数据集转换为图像坐标下的三维坐标格式。
(3)格式转换完成后,通过Matplotlib中的Pyplot库,将三维数据单元数据按等间距不同方向投影分割成一系列切片图片(Slicers),并通过设置图片的Alpha⑩(⑩ Alpha通道是一个8位的灰度通道,该通道用256级灰度来记录图像中的透明度信息,定义透明、不透明和半透明区域,其中黑表示全透明,白表示不透明,灰表示半透明)值改变图片的透明度。为了获得更好的可视化效果,需要对每个切片图片做“剪裁”操作,也就是设定每个切片所要展现的通量数值范围,最后将约900张图片集存放在指定位置备用。处理前后对比图如图 2,通过对比可以发现适当方法可以有效地减少每个切片图片的噪声,这样在重建后使得数据结构更清晰。

|
| 图 2 “Adaptive”处理前后效果对比,左为处理前,右为处理后 Fig. 2 Comparison of images before and after the adaptive processing (in the left and right panels,respectively) |
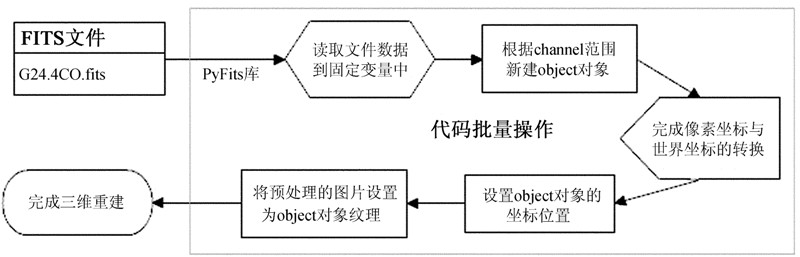
将已处理的图片作为纹理贴图到新建的目标对象上,并完成图像坐标向世界坐标的转换,设置目标对象纹理时使用的是UV贴图,可以在Blender的3D Viewport中不通过渲染,使用Texture Mode实时、多角度观察重建的三维模型的结构特征,具体流程如图 3。
|
| 图 3 三维模型重建流程示意图 Fig. 3 A flowchart of constructing a 3D model |
因为Blender内置Python API的特点,可以基于现有的Python科学数据扩展包进行数据分析功能的开发和扩展,这里仅对已开发功能做一个简单介绍。
(1)在三维模型重建完成后,选定特定区域进行数据分析,在Blender的四视图下,可以准确定位兴趣区域。
(2)通过Python的Matplotlib绘图库,绘制选取区域的等高线图(Contours)和三维等高线序列图。
(3)自动将相关参数传到SDSS或NED数据库获得相应的光学波段成图数据,并可以自动保存数据图像以进一步探究该区域是否有恒星或星系。
2.4 小结本工具具有良好的可移植性,不需要配置使用环境,在Blender中导入脚本即可,且图形化界面易于使用和操作。功能上实现了对FITS格式的三维数据单元数据的实时可视化及简单分析,并具有可扩展性,可以通过Python编程补充和完善现有的数据处理功能。
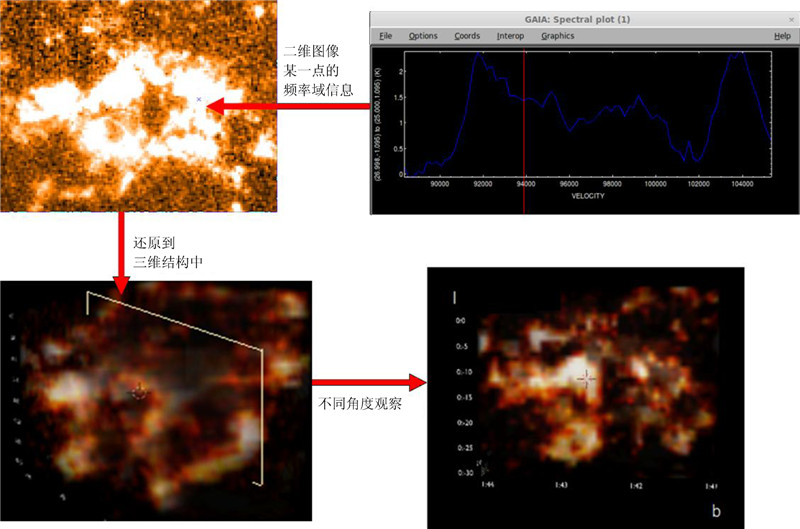
传统的二维处理方式不能解释隐藏规律的特点,而利用三维可视化能够从大量的数据中提取有用的信息,或者得到其他方式不容易观察的数据特征。对于三维数据单元数据,二维图像展示方法丢失的在频率维度的信息可以通过这个工具被展示,根据对应的旋转曲线和速度分布推导出其空间分布关系,并还原到三维模型中,从而得到整体的结构信息。从图 4对G25.4-0.14分子云的二维和三维展示的效果对比中可以发现,在二维图中的结构看上去很像一个环状结构的分子云,但在三维图中环状结构并不明显,很可能是由于投影效应而形成二维的环。根据(1)、 (2)式,还可以把径向速度和分子云的距离相对应。第三维度的径向速度实际上可以看做是分子云的距离,因此图 4展示的是分子云的近似三维空间结构,直接展示了巨分子云复杂的三维空间分布,其中有很多子结构是二维图像无法展示的。
由此可见三维可视化对研究分子云、星系等复杂结构的天体特征及其演化,建立物理模型等有较大的帮助。
|
| 图 4 展示了不同维度的演示效果。左上为利用Starlink软件展示的频率在Frequency=466通道(115.23 GHz)的二维图像,右上为二维图像中某一点的CO(1-0)谱线图,下面两幅是Blender的三维重建模型效果图,以不同的角度展示 Fig. 4 Comparison of the visualization results of different dimensions for the molecular cloud G25.4-0.14. The upper-left panel shows a 2D image observed at the frequency channel 466 (115.23GHz) and displayed using the Starlink package. The upper-right panel shows the spectral-line profile at one location in the image in the upper-left panel. The two bottom panels show the results of the 3D model in different viewing angles |
Blender不仅可以对实测的三维数据单元数据进行三维展示,对于大规模数值模拟(例如N-body模拟)生成的数据也有比较好的可视化效果。在现代天体物理学中,N体模拟是研究各种动力学系统演化的一个重要途径。利用现代超级计算机的优势,大规模的N体模拟已达到数亿级的粒子数规模。N体模拟使得全尺度的天体物理模拟得以达到空前的准确率和所需的动态范围,当然同时也对数据存储和可视化提出了巨大的挑战。下面的例子展示了利用Blender为N体模拟数据进行可视化处理,制作三维动画的过程。
随着SverreAarseth在20世纪60年代开发出第一个NBODY代码——NBODY1,时至今日,新版本的N体模拟的代码NBODY6++[9, 10]正在被不断完善和广泛使用中,它是一个在大规模并行计算机组上运行的、通过图形处理器加速的、用来模拟星团的直接N-body代码⑪(⑪ 直接N-body代码(Direct N-body code)指的是能够直接解运动方程而不需要做任何的假设或者简化,它的优点是计算结果的高度准确性,缺点则是运算复杂度太高) 。NBODY6++运用四阶Hermite积分,并有一系列先进的处理方法例如独立时间帧(Individual Time Step,ITS)、Ahmad-Cohen Neighbor Scheme、KS正则化[11]等等来加速计算。
本例中的数据通过NBODY6++代码,将以Plummer Model⑫(⑫ The Plummer model或Plummer sphere 是一个密度定律,由H.C. Plummer第一次使用来拟合球状星团的观测结果。它经常被N体模拟用作玩具模型(toy model)来模拟恒星系统) 为密度原型的两个球状星团及其碰撞过程模拟出来。为了重构模拟的动态演化过程,输出时按照固定的时间间隔,创建一系列按时间顺序排列的帧(Step#0,Step#1,…,Step#n)。通过Blender工具包开发,导入所有帧中的数据并以动态图的形式展现出来,实现N体模拟数据的动态三维可视化,具体的数据预处理过程和动画实现方法分别见3.1、3.2节。
3.1 数据预处理(1)本例中将NBODY6++模拟的数据存储在HDF5中,HDF5是一个为大规模数值数据集进行优化的高性能IO库。多维度(包括位置、速度、加速度、密度等)的粒子数据以分开的数组存储。通过调用Python处理HDF5格式的扩展库h5py包,可以方便地将模拟数据导入Blender中。
(2)因为在NBODY6++中应用了独立时间帧策略,在给定的时间点仅有活跃粒子(active particles)信息会被整合。星团中心的星经常会交会(即将碰撞但是没有发生碰撞),因此他们的动力学信息必须常更新。相应地,星团边缘的星大多数在不受扰动的轨迹上运动,这也就意味着它们需要少得多的计算。因此,在HDF5输出中,仅存储活跃粒子信息,并通过Hermite scheme为非活跃粒子插入粒子数据,以节省存储空间:
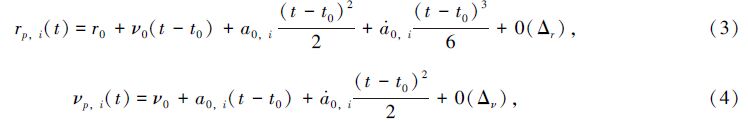
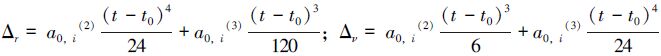 。
。
(3)如果使用回溯查找的方式查询每个缺省粒子的最近更新信息,则每次查找的时间复杂度平均为O(n2),效率很低。这里通过“以空间换取时间”,定义一个定长数组latest_particle[],数组长度为粒子总数,初始化信息为#Step0中每个粒子的属性,按对应ID存放所有粒子的初始状态信息。在每个时间点读取粒子信息时对latest_particle[]数组进行更新,保证数组中存储的是每个粒子的“最新”信息,这样一来查找的时间复杂度降为O(n),减少了时间耗费。
3.2 可视化实现与结论本例中通过Blender中每一个实例对象对应模拟数据一帧的方式实现模型建立,即将数据预处理得到的每一帧的完整粒子信息,给相应的网格数据对象的顶点赋值,然后根据这些网格数据对象创建对应的实例模型。由于一个模拟数据往往包含多个帧,因此需要建立多个模型,但是Python作为脚本语言效率较低,为了提高速度,这一过程可以通过C语言扩展实现。
动态演示部分通过逐帧动画⑬(⑬ 逐帧动画是一种常见的动画形式(Frame By Frame),其原理是在“连续的关键帧”中分解动画动作,也就是在时间轴的每帧上逐帧绘制不同的内容,使其连续播放而成动画) 方法实现。为每一个实例模型的隐藏属性的设置关键帧及其生存时间(Life Time),保证每个实例模型只在固定的时间出现一帧,由于视觉暂留效应,人眼所看到的则是连续的一段动画,并且因为设置关键帧的函数封装在BPY库中,函数调用耗费的时间很低,动画生成的效率较高,并能获得较好的可视化效果,如图 5,由4幅按时间序列的图展示了用NBODY6++代码模拟两个星团碰撞的过程,用户可以选择不同的背景和纹理获得更好的渲染效果,生成形象逼真的动态视频,达到良好的宣传和出版效果,在上传的视频⑭(⑭ 视频链接http://i.youku.com/u/UMTQ2MzYxNzY5Ng==/playlists) 中展示了利用Blender制作的三维可视化动画。

|
| 图 5 N体模拟效果图 Fig. 5 Our Blender-based 3D visualization of an N-body simulation sequence |
由于Blender并不是专业的天文软件,对于数据的分析等功能扩展必须依赖于Python脚本编程完成,因此相对于Paraview⑮(⑮ http://www.paraview.org/) 等专门作数据处理的软件来说,性能方面有一定的局限性。但相比之下,专业处理软件往往更专注于分析和计算功能,在可视化效果方面较差,因此可以通过开发展示N-body simulation数据的工具包作为辅助工具,将科学成果用更直观、更美化的方式展现给读者。
4 结 论作为传统数据处理模式的补充和完善,三维可视化不仅可以补充二维显示对信息丢失的缺陷,还可以通过分析整体结构获得更多的信息。对于天文学这样一门以数据为研究基础的学科来说,三维可视化研究正逐渐成为数据分析中不可缺少的一部分。
本文使用非天文软件Blender,根据所处理的天文数据类型、所关注的研究重点,选取相应的可视化技术,结合Python脚本编程和Blender封装的BPY库,开发了分别针对三维数据单元数据和N体模拟数据结果的三维可视化工具包,通过此工具包不仅使得所演示的三维模型的相关参数符合科学性,并且三维实时多角度的显示也使得科学家对数据的三维结构特征有一个很好的把握,从而有助于进一步研究天体结构演化和模型建立。在未来的研究中,进一步完善和扩充现有工具包的展示和分析功能,并尝试与其它现有成熟的天文分析工具包整合,得到一个三维可视化与数据处理分析功能并存的软件包。
| [1] | Brown R L, Wild W, Cunningham C. ALMA-the Atacama large millimeter array[J]. Advances in Space Research, 2004, 34(3): 555-559. |
| [2] | Johnston S, Bailes M, Barlel N, et al. Science with the Australian Square Kilometre Array Pathfinder[J]. Publications of the Astronomical Society of Australia, 2007, 24: 174-188. |
| [3] | Goodman A A. Principles of high-dimensional data visualization in astronomy[J]. Astronomische Nachrichten, 2012, 333(5-6): 505-514. |
| [4] | Hess R. Blender foundations: the essential guide to learning Blender 2.6[M]. Burlington: Focal Press, 2010. |
| [5] | Kent B R. Visualizing astronomical data with Blender[J]. Publications of the Astronomical Society of the Pacific, 2013, 125(928): 731-748. |
| [6] | Tully R B, Shaya E J, Karachentsev I D, et al. Our peculiar motion away from the Local Void[J]. The Astrophysical Journal, 2008, 676(1): 184-205. |
| [7] | Ai M, Zhu M, Xiao L, et al. Properties of the UCHII region G25.4NW and its associated molecular cloud[J]. Research in Astronomy and Astrophysics, 2013, 13(8): 935-944. |
| [8] | Greisen E W, Calabretta M R. Representations of world coordinates in FITS[J]. Astronomy and Astrophysics, 2002, 395: 1061-1075. |
| [9] | Spurzem R. Direct N-body simulations[J]. Journal of Computational and Applied Mathematics, 1999, 109(1-2): 407-432. |
| [10] | Spurzem R, Berentzen I, Berczik P, et al. Parallelization, special hardware and post-Newtonian dynamics in direct N-Body simulations[M]//The Cambridge N-Body Lectures. Germany: Springer, 2008: 377-389. |
| [11] | Aarseth S J. Gravitational N-body simulations: tools and algorithms[J]. Britain: Cambridge University Press, 2010. |



