2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
卫星定位系统的精度主要取决于两方面:一是观测卫星在空间的分布情况,通常称为卫星分布几何图形;二是各观测量的精度。为评价定位结果,常采用精度因子(Dilution of Precision,DOP)的概念,也称为卫星图形强度因子或精度衰减因子。由此,最终定位解算结果可表示为
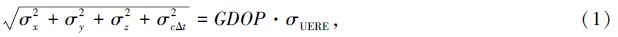
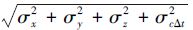 为坐标位置与接收机时钟误差;σUERE为用户等效伪距测量误差。
为坐标位置与接收机时钟误差;σUERE为用户等效伪距测量误差。
GDOP及σUERE的改变均能对定位误差造成影响。当可视卫星数目增加时GDOP值随之单调递减,从而能够获得更优的定位精度。当卫星数目多于4颗时,常采用最小二乘算法(Least Square method,LS)进行解算。若各测量值之间相互独立且符合高斯正态分布,则最小二乘算法能够使得各观测伪距具有最小残差平方和,从而获得最优估计解。然而,在顾及电离层延迟、对流层延迟及多路径误差等情况下,各实际测量值之间往往不是相互独立,也不是同分布的,甚至并不符合正态分布。此时,若仍沿用最小二乘算法则难以保证其最优性。这种情况下,可以引入某个加权矩阵W,改变不同卫星之间的权重,更合理地估计最优位置解。这种方法称为加权最小二乘估计算法(Weighted Least-Square estimate,WLS)[1, 2, 3, 4]。
加权最小二乘估计算法更符合实际定位情况,能够对各观测卫星进行更合理的衡量,获得更高的解算精度。权矩阵W最常用的方法是作为一个对角矩阵W=diag(ω1,ω2,…,ωn),对角元素ωi(i=1,2,…,n)为定位解算中第i颗卫星的权重系数,通过将伪距误差方差对仰角作近似而获得,随着仰角的减小而单调递增[1]。加权最小二乘估计算法求解中采用这样一个协方差使得低仰角卫星的权重降低,因为那些卫星由于典型的多径特征和残留的电离层、对流层误差而噪声较大[1, 5]。目前有一些关于加权新方法的有益探讨和研究,文[3]利用模糊数学方法确定加权矩阵,文[6]提出将灰色关联分析法与广义延拓数学方法相结合构造权矩阵。然而,由于σUERE取决于伪距测量精度、卫星仰角及卫星星历数据质量等多种因素,其间还存在错综复杂的相互作用,因此权矩阵的构造与确定一直是一个难题[2, 3, 5]。本文提出了一种新的加权最小二乘算法,通过分步构造加权矩阵的方法对各未知数进行分离解算。并且,通过全球定位系统实测实验对方法的可行性和精度水平进行了分析与验证。
1 卫星定位中的加权最小二乘算法
卫星导航定位中,测量得到用户至各观测卫星的伪距值后,即可构造得到地心地固坐标系(ECEF)下的观测方程:
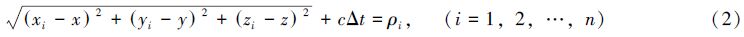
方程组(2)经线性化处理后可得
GΔX=Δρ,
(3)
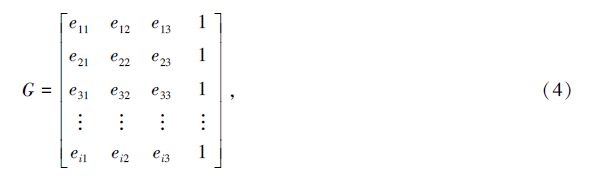
ΔX为近似解与真解的偏差向量:
ΔX=[ΔxΔyΔz-cΔt]T.
(5)
Δρ为伪距观测值向量:
Δρ=[Δρ1Δρ2Δρ3Δρ4]T.
(6)
可以看出,真正求解的是用户位置与时钟误差初值估计的校正量ΔX。记ΔX的最大似然估计为
Δ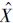 ,并定义如下:
,并定义如下:
Δ
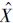 =arg max p(Δρ/ΔX),
=arg max p(Δρ/ΔX),
(7)
若测量误差之间相互独立,且均符合均值为0、方差为σ2的高斯分布,则(7)式变为
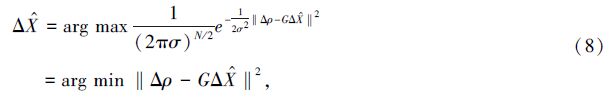
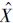 ‖2对Δ
‖2对Δ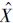 求微分,则可将(8)式变换为
求微分,则可将(8)式变换为
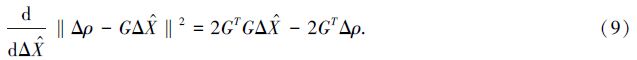
Δ
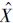 =(GTG)-1GTΔρ.
=(GTG)-1GTΔρ.
(10)
由于在实际定位中,各测量伪距不仅不是同分布、等精度的,而且还是相互关联的,因此需要考虑更一般化的情况。此时,最大似然估计Δ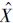 可以表示为
可以表示为
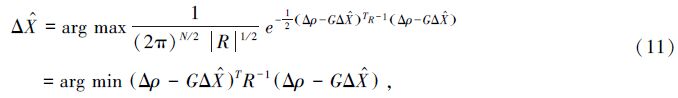
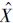 求微分,并令其等于0可得
求微分,并令其等于0可得
Δ
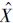 =(GTR-1G)-1GTR-1Δρ.
=(GTR-1G)-1GTR-1Δρ.
(12)
Δ
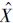 =(GTWG)-1GTWΔρ,
=(GTWG)-1GTWΔρ,
(13)
由上述讨论可知,最小二乘算法的目标函数可表示为

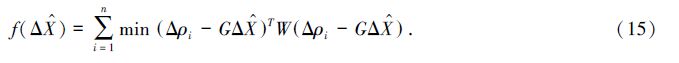
然而,最小二乘与加权最小二乘算法的数学估计目标均是使得全局残差和最小,即使得X、Y、Z
各坐标方向上的残差平方和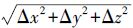 达到最小,而各方向上单独的残差Δx、Δy、Δz却不一定是最小的。因此,针对这个问题提出一种对各未知数、各坐标方向依次分步进行加权解算的方法。在每一次单独的估计解算过程中,并不要求全局残差最小,而是使得各未知数的独立残差达到最小,即将数学目标函数改变为
达到最小,而各方向上单独的残差Δx、Δy、Δz却不一定是最小的。因此,针对这个问题提出一种对各未知数、各坐标方向依次分步进行加权解算的方法。在每一次单独的估计解算过程中,并不要求全局残差最小,而是使得各未知数的独立残差达到最小,即将数学目标函数改变为
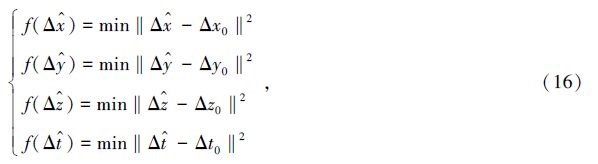
这样,通过对各未知数依次分步进行相应的加权计算,改变原有解算模式,达到对各未知数进行分离解算的目的。此时不再要求权矩阵W使得所有未知数的全局残差最小,而是分别使得各个未知数各自的单一残差最小化,并认为此时为该未知数的最优估计。最后,将各坐标方向上依次所得的最优估计值组合在一起,构成一组新的矛盾解,作为用户位置坐标的最优估计。
2.2 实现方法
将(13)式中的(GTWG)-1GTW项作为一个整体,并记为
H=(GTWG)-1GTW.
(17)


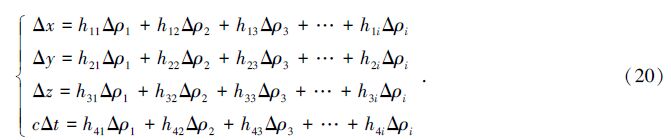
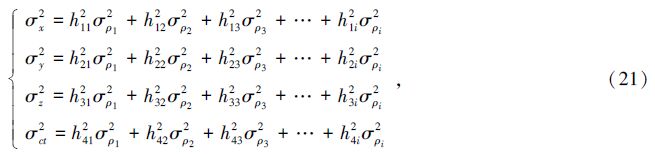
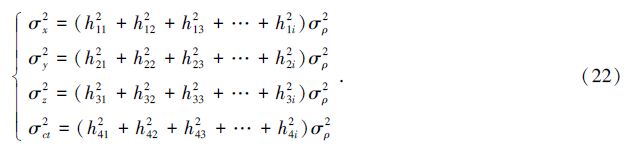
min(h112σ2ρ1+h122σ2ρ2+h132σ2ρ3+…+h1i2σρi2).
(23)
对未知数x作出最优估计后,同理再对其他各未知数依次进行解算即可。这种思想,就是先构造一个权矩阵W,改变解算过程中误差的分布和影响,使得X方向上的误差估计最小;再构造另一个权矩阵W,使得Y方向上的误差估计最小,依次类推。最后,将各未知数的最优估计值组合在一起,构成一组新的矛盾解,作为用户位置坐标的最优解。为获得更高精度的解算结果,该方法的解算过程并非一步完成,而是分为若干个步骤,故称为“分步加权解算方法”。
2.3 加权矩阵W的构造 2.3.1 多元函数极值求解构造方法
以5颗卫星时的解算情况为例,当i=5时,方向余弦系数矩阵G为

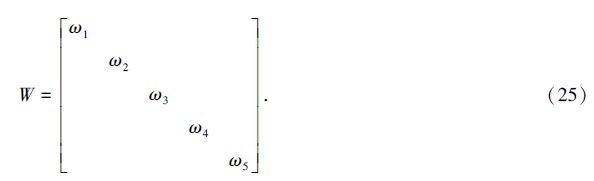
hji=fji(ω1,ω2,ω3,ω4,ω5) (i=1~5,j=1~4).
(26)
将(26)式得到的各项hji表达式及各卫星测量等效伪距误差值σρi(i=1,2,…,5)一起代入(21)式,可构造分别对应于未知数x、y、z和Δt的目标函数:
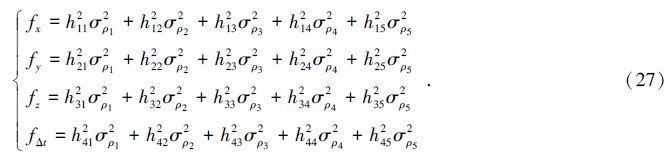
同理,可以依次得到其余各变量各自的最优估计值。此过程中,W为一正定对角矩阵,各对角元素满足下列归一化要求:
ω12+ω22+…+ωi2=1 (0<ω1,ω1,…,ωi<1).
(28)
这样,既把权矩阵数据映射到0~1的范围内进行处理,也为多元函数的极值求解提供了区间范围约束条件。当卫星数目较多时,无论多元函数是否为凸函数特性,均能够在约束条件和区间内求解得到其局域极值点。具体的极值求解算法,可采用极速下降法、单纯形法等常用的非线性求解算法[8, 9, 10]。
2.3.2 可能性模板矩阵构造方法多元函数极值求解的方法能够从数学原理上严格确定权矩阵元素的值,但在实际运用中,对一个多元函数求极值的计算不仅繁琐,还需花费大量的计算时间,限制了方法的实用性。为此,可在求解过程中结合实际情况引入枚举组合的方法,对权矩阵中各对角元素的可能取值进行列举与排列组合。在解算中,根据函数值极小化的判定条件进行计算和判断,筛选出最优的一组权值组合。
采用这种方法时,无需在每一次的定位解算中实时计算和生成各个可能性权矩阵W,而可以事先固定和存储符合条件的一系列正定对角矩阵,作为“可能性权矩阵模板”。以5颗观测卫星为例,若令最小权值ωmin2=0.1,则其最大权值ωmax2=1-(5-1)×0.1=0.6,由此生成的可能性模板矩阵形式如下:
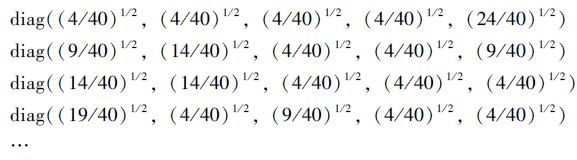
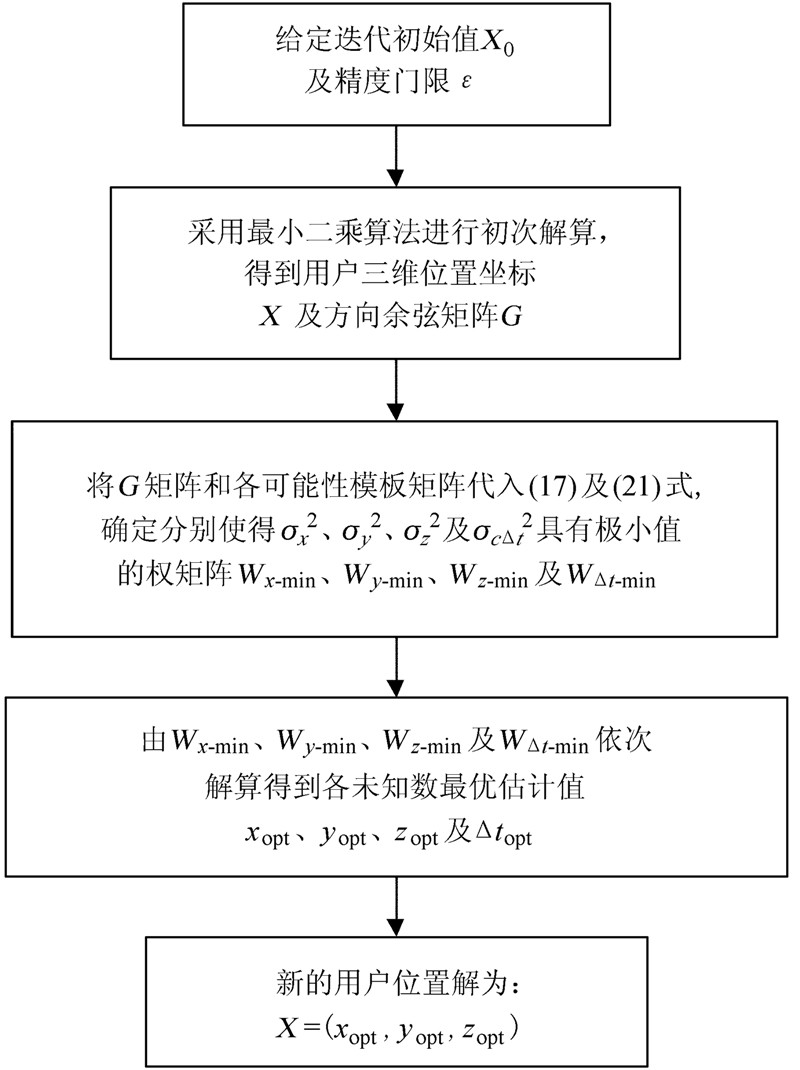
在分步加权解算时代入这些模板矩阵进行计算,并根据判定条件选出最合适的矩阵模板作为最终权矩阵W即可。这样,虽不能严格计算获得使目标函数极小化的权矩阵元素值,但却能够避免权矩阵的反复构造,减少计算量,提高解算速度,在算法准确性与实用性上取得更好的平衡。由此,分布加权解算算法的使用步骤可表示为图 1。
|
| 图 1 分步加权解算方法流程示意图 Fig. 1 A schematic diagram of the method for multiple-step Weighted Least-Square estimate |
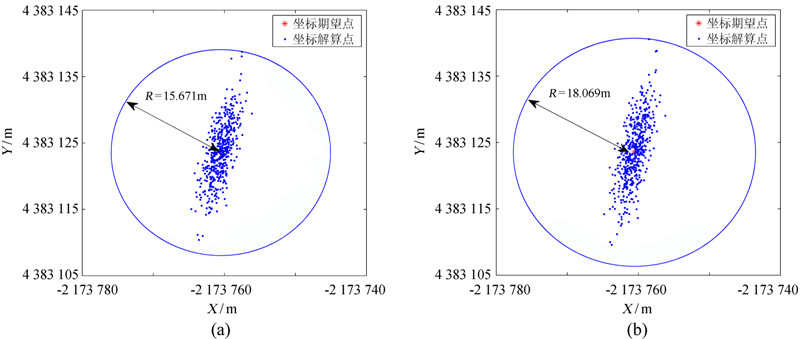
为验证方法的可靠性,在北京地区某地对全球定位系统卫星进行了连续观测,并选出了5颗具有最佳精度因子值的可视卫星进行绝对单点定位。定位数据输出时间间隔为1 s。利用输出数据在Matlab仿真软件中分别采用最小二乘算法和分步加权解算方法进行坐标解算,两种方法的定位点分布情况如图 2。
|
| 图 2 定位解算点分布情况示意图。(a) 最小二乘算法定位点分布;(b) 分布加权算法定位点分布 Fig. 2 Distributions of position solutions for satellite positioning. (a) A distribution from the LS method; (b) A distribution from the new method |
从图 2可以看出,分布加权算法相对于最小二乘算法有着明显的改善,减小了误差分布的范围。统计其误差特性结果,如表 1。
| 统计特性/m | 最小二乘算法 | 分步加权算法 |
| X方向平均误差 | 0.996 | 0.973 |
| Y方向平均误差 | 3.973 | 3.565 |
| Z方向平均误差 | 2.299 | 1.965 |
| 三维方向平均误差 | 4.883 | 4.369 |
| X方向均方根误差 | 1.268 | 1.242 |
| Y方向均方根误差 | 4.938 | 4.389 |
| Z方向均方根误差 | 2.913 | 2.453 |
| 三维方向均方根误差 | 5.871 | 5.177 |
由表 1中的误差统计特性可知,在同等条件下进行定位解算,无论是在各坐标方向还是三维位置方向上,分步加权算法都能够获得更准确的定位结果,提高三维定位精度0.7 m(均方误差),减小相对误差约10%~20%。并且,分步加权算法在各坐标轴方向和三维位置上的均方根误差都比最小二乘算法更小,说明定位解的波动较小,方法具有更高的稳定性。
在解算时间上,最小二乘算法单点定位解算平均耗时约为4.92×10-4s;分步加权算法由于有着对可能性模板矩阵进行数值计算及再次求解位置坐标的过程,单点定位解算的平均耗时约为3.10×10-3s。
4 总 结本文从卫星定位线性测量方程组出发,通过研究迭代解算过程中伪距测量误差对待求未知数误差的放大规律,提出了一种加权最小二乘解算方法,及其权矩阵的具体构造与实现方法。该方法对测量方程组中的各个未知数进行分步加权与单独解算,在每一次的权矩阵构造过程中,并不要求测量方程组的全局伪距残差和最小,而是依次构造使得各个未知数达到独立最优估计的权矩阵W,对未知数进行分离解算;最后,将分步解算得到的各未知数最优估计值作为新的用户坐标位置。通过仿真计算与分析,表明该分步加权解算方法能够在各坐标轴方向和三维坐标方向上提高定位解的精度。
该方法也存在着一些需要继续研究和改进的问题,主要体现在:
(1)方法需要利用各观测卫星等效伪距测量误差的先验统计信息。这些信息会在卫星星历中给出,但在实际定位时却通常不会严格一致,因此会给权矩阵的计算带来误差,从而影响算法的精度。
(2)由于方法复杂度更高,因此增加了计算耗时。虽然仍能满足一般性的、非高动态实时单点定位需求,但在观测卫星数目较多时,仍然需要考虑和研究更为简单与快速的权矩阵确定方法,以减少计算量,提高解算速度,使算法具有更好的实用性和可靠性。
| [1] | Kaplan E D, Hegarty C J. Understanding GPS: principles and applications[M]. 2nd ed. UK: Artech House London, 1996. |
| [2] | Sairo H, Akopian D, Takala J. Weighted dilution of precision as quality measure in satellite positioning[J]. IEEE Radar, Sonar and Navigation, 2003, 150(6): 430-436. |
| [3] | Yang Y, Miao L J. GDOP results in all-in-view positioning and in four optimum satellites positioning with GPS PRN codes ranging[C]//PLANS 2004 Position Location and Navigation Symposium. 2004: 723-727. |
| [4] | 丛丽, Ahmed I Abidat, 谈展中. 卫星导航几何因子的分析和仿真[J].电子学报, 2006, 34(12): 2204-2208. Cong Li, Ahmed I Abidat, Tan Zhanzhong. Analysis and simulation of the GDOP of satellite navigaion[J]. Acta Electronica Sinica, 2006, 34(12): 2204-2208. |
| [5] | Misra P, Enge P. Global Positioning System-Signal, Measurements, and Performance[M]. 2nd ed. Lincoln: Ganga-Jamuna Press, 2006. |
| [6] | 宁春林, 施浒立, 李圣明, 等. 一种构造WDOP中加权矩阵的新方法[J]. 宇航学报, 2009, 30(2): 526-531. Ning Chunlin, Shi Huli, Li Shengming, et al. A new method of constructing weighting matrix of WDOP[J]. Journal of Astronautics, 2009, 30(2): 526-531. |
| [7] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003. |
| [8] | 王世儒, 王金金, 冯有前, 等. 计算方法[M]. 第二版. 西安: 西安电子科技大学出版社, 2004. |
| [9] | 席少林, 赵凤治. 最优化计算方法[M]. 上海: 上海科学技术出版社, 1983. |
| [10] | Zaguskin O O. Solution of Algebraic and Transcendental Equations[M]. New York: Pergamon Press, 1961. |


