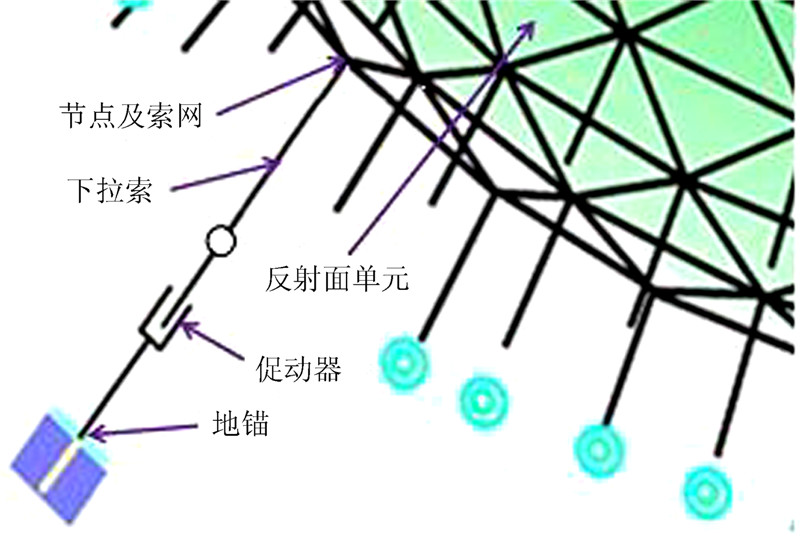
500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope,FAST)是国际上最大、最灵敏的射电天文望远镜[1]。利用贵州喀斯特洼坑作为台址,在洼坑内铺设500 m球冠状反射面,通过主动控制形成抛物面以汇聚电磁波,采用轻型钢索拖动馈源平台实现望远镜的指向跟踪。图 1为FAST望远镜主动反射面工作原理示意图。
|
| 图 1 主动反射面工作原理 Fig. 1 Illustration of the operation of the main active reflector antenna |
在望远镜观测时,采用促动器驱动下拉索方式改变反射面单元面型,以跟踪天体。促动器为机、电、液一体化单元,工作于贵州黔南潮湿洼地中,始终承受最大6~10×103 kg拉力变载荷作用,平均速度约0.2 mm/s,数量为2 225套,部分促动器处于连续工作状态,发生故障不可避免[2]。望远镜设计寿命30年,故障促动器将降低望远镜使用效率及面型精度。同时,促动器分布较广,洼地坡面崎岖、陡峭,见图 2,且被下拉索、促动器、法兰及地锚阻挡,现场维护条件较差。

|
| 图 2 促动器使用陡坡 Fig. 2 The slope on which an actuator is positioned |
针对大射电天文望远镜维修问题,有必要设计一种故障促动器快速拆换机构,其设计要求包括:结构简单,安全可靠,重量轻,易携带,拆换方便快速,出力大,可长期保持大载荷。
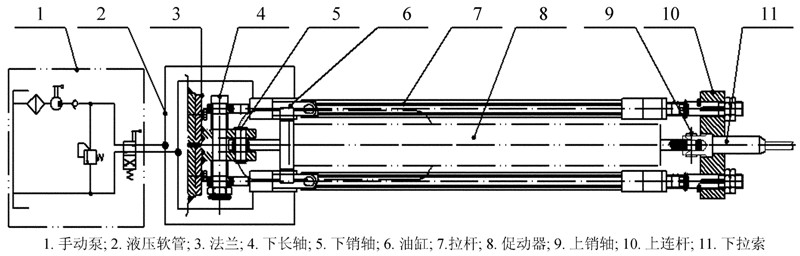
1 方案设计图 3为一种故障促动器拆换机构设计方案[3]。其工作顺序为:(1)组装拆换机构,与下拉索、法兰接口连接;(2)采用左、右同步油缸加载,转移故障促动器载荷;(3)依次拔出故障促动器上销轴、下销轴;(4)油缸保压,更换新促动器,依次插上促动器下销轴、上销轴;(5)促动器加载,转移拆换机构载荷;(6)拆卸与下拉索、法兰接口结构,取走拆换机构。方案设计时,有以下4方面考虑。
|
| 图 3 促动器拆换方案 Fig. 3 Our design of a mechanism for dismounting and assembling an actuator |
促动器下端与法兰销轴连接,为与拆换机构连接,法兰采用双孔设计,该安装靠近地面,可接近性好。而促动器故障可能发生在运行的任一时刻,促动器上端与下拉索销轴连接,该销轴与地面之间的轴向距离约1.8~3 m,促动器轴线最大竖直夹角约56°,部分洼地坡面较陡,该销轴与地面之间的铅垂距离将大于3 m。为快速、方便安装拆换机构,图 3上连杆为开口非封闭C型结构,安装过程地面作业,无需空中操作。安装过程:(1)两侧拉杆与上连杆地面连接;(2)利用拉杆举起上连杆;(3)上连杆开口穿过直径较小的下拉索索体;(4)用力向下拉紧两侧拉杆,拉杆与下拉索锚具配合,完成安装。
1.2 加载安全可靠调节左右拉杆初始长度后,加载装置完成最大1×104 kg载荷施加。加载方式选择因素包括:(1)载荷较大,单侧拉杆为5×103 kg;(2)重量轻,易携带;(3)左、右两侧拉杆同时加载,需要同步;(4)尽量远程操作,避免发生事故;(5)技术成熟,常规设计。考虑到液压传动具有功率重量比大、负载大、可远距离控制、易实现直线往复运动等优点,设计了由手动泵、快插接头、软管、左油缸与右油缸组成的手动液压加载方案,见图 3,该方案可实现以上要求[4, 5]。
1.3 拉杆地面调节长度可调拉杆的设计要求包括:(1)促动器行程1.2 m,故障可能发生在0~1.2 m任一位置,这要求左、右拉杆长度1.2 m可调;(2)长度调节后,拉杆应可靠锁紧;(3)因拉杆与上连杆先挂在下拉索锚具上,人应在地面可控制拉杆长度调节或锁紧;(4)重量轻,易携带。
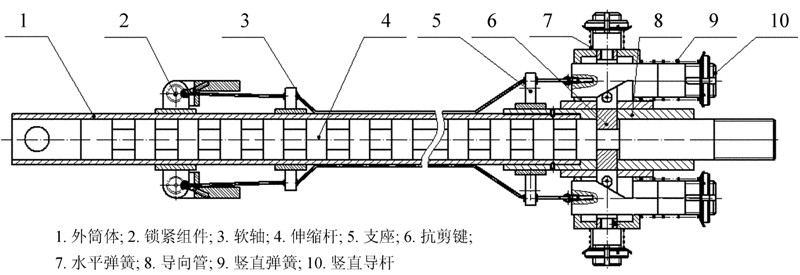
图 4是一种拉杆设计方案,其原理是软轴控制竖直导杆的升降,利用其斜面推动抗剪键上的滚轮,完成抗剪键的伸缩,进而控制抗剪键与伸缩杆环形槽啮合或脱开,实现伸缩杆的锁紧或调节。软轴通过轴向固定的外层钢片套及非金属保护层,实现软轴的远距离控制。
|
| 图 4 拉杆设计方案 Fig. 4 Our design of a pull rod |
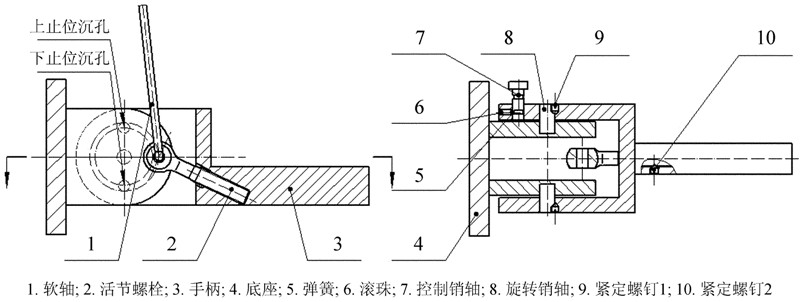
拉杆锁紧组件如图 5,软轴下侧与活节螺栓连接,手柄旋转±90°可实现软轴伸与缩。底座设计了下止位沉孔与上止位沉孔,控制销轴与沉孔配合可将软轴在两状态终止位置锁紧。控制销轴加工了两个半圆槽道,可与手柄上弹簧压紧的滚珠配合,实现防止控制销轴脱落以及可靠锁紧的功能。
|
| 图 5 锁紧组件 Fig. 5 Our design of the component for locking |
促动器与下拉索的连接销轴与地面之间的轴向距离约1.8~3 m,故障促动器卸载后,人手必须可触碰到该销轴,才能完成拆换。为此,利用左拉杆左侧、右拉杆右侧各焊接4根短轴,如图 6,铝制爬梯卡在短轴上,通过爬梯,人可实现销轴的拆换。

|
| 图 6 爬梯 Fig. 6 Our design of the ladder |
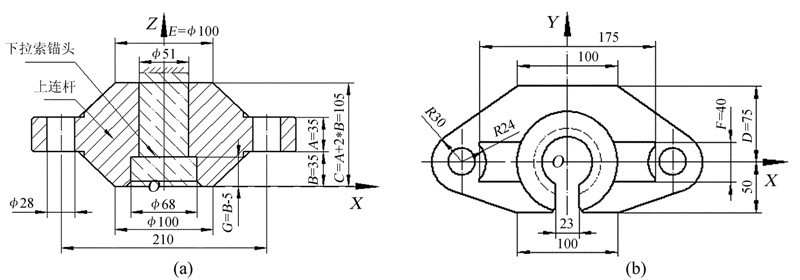
如图 7,上连杆开口尺寸23 mm,另一侧尺寸100 mm增强开口刚度,4组筋板增强抗弯能力,中心孔直径分别为51 mm与68 mm,保证与下拉索锚头紧密配合。材料为40 Cr,焊接而成。该结构是与下拉索快速连接的保证,其设计重点为大载荷下开放式结构的应力、变形及质量。为此,采用有限元方法对该零件进行分析[6, 7]。
|
| 图 7 上连杆结构示意图。(a)主视图;(b)俯视图 Fig. 7 Our design of the upper-connecting rod. (a) The front view; (b) The top view |
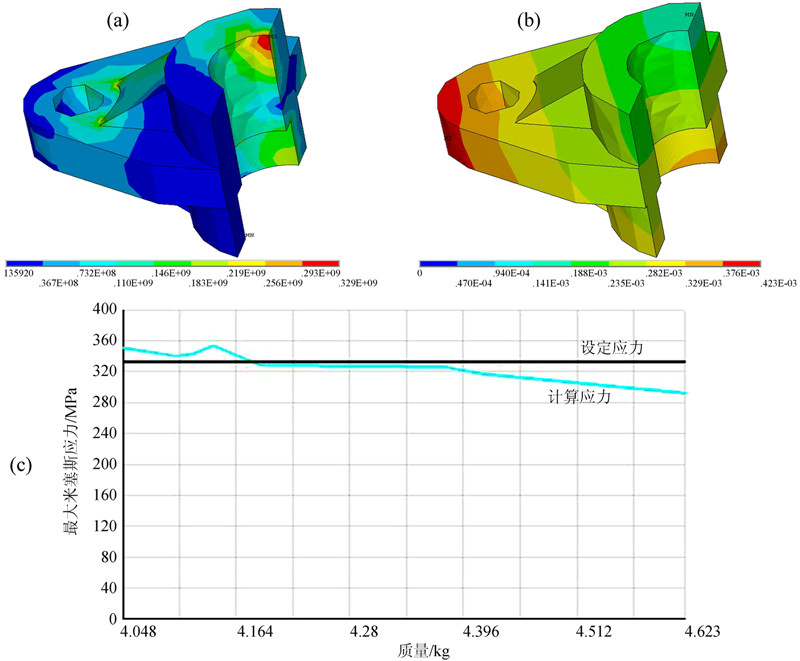
上连杆结构及载荷具有对称型,建立其1/2模型,利用有限元方法进行强度计算。下拉索锚头顶面固定,单侧施加5×103 kg载荷,上连杆与下拉索锚头结合面采用面面接触非线性分析方法。考虑加工、装配及促动器故障姿态,由上连杆、左右拉杆及油缸、下长轴组成的长方形框架存在不在同一平面情况,仿真时在Φ28孔位置施加1×103 kg侧向载荷,方向为自开口向后的最为恶劣状态。以静强度计算为基础,进行轻量化分析。目标函数为质量,状态变量为许用应力,设计变量为A、B、D,(1)式给出了其优化数学模型。
优化分析结果见图 8,最大应力为329 MPa,位于筒体后母线上端,最大位移为0.423 mm,发生在Φ28孔左端部,且上连杆不会因开口扩展而失效,满足使用要求。模型质量4.2 kg,整体质量8.4 kg,为原结构的91%。依据优化结果,A、B、D分别取整为30 mm、39 mm、68 mm。
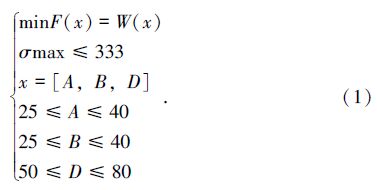
|
| 图 8 优化分析结果。(a)应力云图;(b)变形云图;(c)最大应力与质量关系 Fig. 8 Our optimization-analysis results for the upper-connecting rod. (a) The stress distribution; (b) The deformation distribution; (c) The relation between maximum stress and mass |
抗剪键伸缩是否灵活是拉杆长度调节的关键,其运动顺序为:啮合→下拉→脱出→上松→啮合。以力学分析为基础,部分变量初始值为:抗剪键水平位移10 mm,斜面倾角θ=60°,竖直导杆位移为10tanθ=17 mm。假设竖直弹簧17 mm变形对应载荷变动ΔFsv=10-15 kg,计算水平弹簧10 mm变形对应载荷变动ΔFsh=10-5 kg是否满足抗剪键运动控制要求。
2.2.1 抗剪键处于啮合状态
先选竖直导杆为研究对象,其受力分析如图 9(a),按图示坐标轴列出平衡方程[8]:
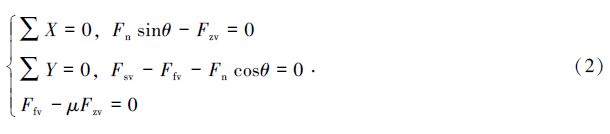
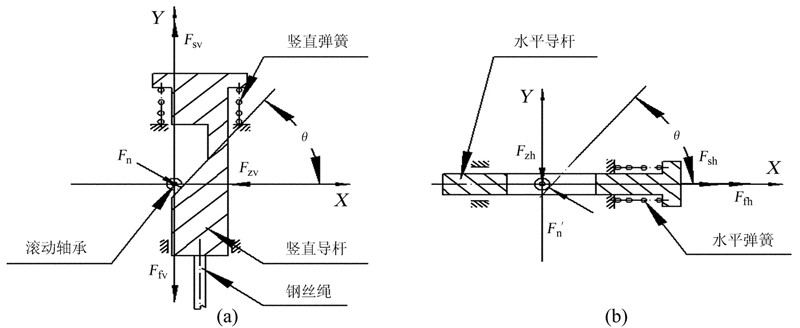
|
| 图 9 啮合状态受力分析。(a)竖直导杆;(b)水平导杆 Fig. 9 Our force analysis for the meshing state. (a) Forces in the vertical guide rod; (b) Forces in the horizontal guide rod |
求解方式组(2),可得Fn=155 N。再选水平导杆为研究对象,其受力分析如图 9(b),法向力Fn与Fn′为作用力与反作用力,按图示坐标轴列出平衡方程:
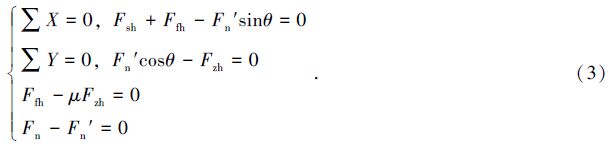
竖直导杆,Fn接近为0,Ffv亦接近为0,在大于Fsvmax=150 N的钢丝绳拉力作用下,竖直导杆将向下运动。水平导杆,Fn′接近为0,Ffh亦接近为0,伸缩杆作用到抗剪键上的摩擦力Ffmax=umg/2=11 N,方向为图 9(b)X轴负向,小于Fshmin=50 N,水平导杆将克服该摩擦力水平退出啮合沟槽。
2.2.3 抗剪键处于脱出状态手柄处于锁紧状态,抗剪键退出伸缩杆啮合沟槽,外筒体及导向管可沿伸缩杆自由滑动,调节二者的相对长度。
2.2.4 竖直导杆处于上松状态平衡方程同啮合状态,Fsv自150 N减小至100 N。计算始末水平弹簧力,Fsh_first=182 N,大于50 N,水平导杆能够开始向左运动;Fsh_end=121 N,大于100 N,水平导杆可进入啮合沟槽。
根据载荷与变形要求,通过优化设计,确定弹簧的有关参数如下。
竖直弹簧:小径d=3 mm;中径D=38 mm;材料65 Mn;弹簧自由高度H0=100 mm;节距t=16.5 mm;弹簧的最大压缩量81 mm;工作圈数n=6;当载荷为150 N时,弹簧压缩量为59 mm;当载荷为100 N时,弹簧压缩量为42 mm。
水平弹簧:小径d=2.5 mm;中径D=32 mm;材料65 Mn;弹簧自由高度H0=40 mm;节距t=14.7 mm;弹簧的最大压缩量30.3 mm;工作圈数n=2.5;当载荷为100 N时,弹簧压缩量为21.2 mm;当载荷为50 N时,弹簧压缩量为10.5 mm。
斜面最大法向力Fnmax发生在上松开始阶段,大小为Fsv/(μsinθ+cosθ)=233 N,轴承选用深沟球轴承619/4,其基本额定载荷Cr=0.95 kN,C0r=0.35 kN。
钢丝绳拉力最大值为150 N,选用6×7+IWS钢芯钢丝绳,公称抗拉强度1 470 MPa,直径为2 mm,最小破断拉力为2.11 kN。
通过抗剪键整个运动过程分析,ΔFsh=10-5 kg可以满足抗剪键的运动控制要求。同时,该分析为弹簧、轴承、钢丝绳的设计与选型提供了依据。
3 结 论FAST望远镜建成后,快速拆换机构将是促动器运行维护的必要条件。基于接口便于安装、加载安全可靠、拉杆地面调节、拆换销轴爬梯的设计要点,提出了一种拆换机构设计方案,并对其关键技术进行了分析:
(1)利用有限元方法,分析了开口非封闭C型上连杆承受轴向载荷与侧向载荷的最不利工况,结果表明:最大应力329 MPa,最大变形0.423 mm,且上连杆不会因开口扩展而失效,满足其使用要求。经轻量化分析,质量减轻为原结构的91%;
(2)以力学分析为基础,假设竖直弹簧变形17 mm,载荷变动为10-15 kg,计算了水平弹簧变形10 mm,载荷变动可为10-5 kg,则抗剪键运动平顺、伸缩可控、锁紧可靠。
文中阐述的设计方案、分析思路及计算方法可用于后续FAST故障促动器快速拆换机构物理样机研制,也对解决同类重型加载装置的拆换具有借鉴意义。
| [1] | Nan Rendong. Five hundred meter aperture spherical radio telescope (FAST) [J]. Science in China: Series G Physics, Mechanics & Astronomy, 2006, 49(2): 129-148. |
| [2] | 李宁, 薛建兴, 王启明. FAST促动器的设计与仿真[J]. 机械设计与制造, 2012(11): 55-57. Li Ning, Xue Jianxing, Wang Qiming. The design and simulation of FAST actuator[J]. Machinery Design and Manufacture, 2012(11): 55-57. |
| [3] | 薛建兴, 王启明. 一种大射电天文望远镜下拉索驱动装置快速更换机构: 中国, 201220060401.2[P]. 2012-09-05. |
| [4] | 韩桂华, 王景峰, 乔玉晶. 液压系统设计技巧与禁忌[M]. 北京: 化学工业出版社, 2012. |
| [5] | 左健民. 液压与气压传动[M]. 北京: 机械工业出版社, 2005. |
| [6] | 薛建兴, 古学东, 王启明, 等. 考虑接触间隙的FAST节点轻量化分析[J]. 机械设计, 2013, 30(9): 50-53+77. Xue Jianxing, Gu Xuedong, Wang Qiming, et al. Lightweight analysis of FAST connection with clearances[J]. Journal of Machine Design, 2013, 30(9): 50-53+77. |
| [7] | 高耀东, 刘学杰. ANSYS机械工程应用精华50例[M]. 北京: 电子工业出版社, 2011. |
| [8] | 王铎, 赵经文. 理论力学[M]. 北京: 高等教育出版社, 2000. |


