| 基于熔渣离子分子共存理论的CaO-MgO-SiO2-FeO-Al2O3熔渣黏度预测模型 |
2. 高端金属材料特种冶炼与制备北京市重点实验室,北京 100083
2. Beijing Key Laboratory of Special Melting and Preparation of High-End Metal Materials, Beijing 100083, China
熔渣黏度是钢铁冶炼过程中的一种基本性质。黏度对熔渣流动性、渣金反应、泡沫渣的发泡能力等具有极其重要的作用。高温黏度的测量耗时长,通过实验无法对每一种熔渣的黏度进行测量[1]。因此,建立熔渣黏度模型是研究熔渣黏度参数的一种较为便捷的途径。
目前,熔渣黏度模型可分为3类,即熔渣温度—黏度模型、熔渣成分—黏度模型、熔渣结构—黏度模型[2]。熔渣黏度与其结构密切相关,熔渣成分不同,其结构也会存在差异。其中,熔渣结构—黏度模型目前已经成为备受关注的模型之一。
目前,对于含FeO的熔渣渣系可使用的熔渣黏度模型有Riboud模型[3]、Mills模型[4]、Shu熔渣结构模型[5-6]及基于熔渣离子分子共存理论的熔渣黏度模型[7-8]。Riboud模型是基于Weymann-Frenkel黏度公式和Urbain模型[9],结合高炉熔渣黏度数据,得出简单的熔渣成分和黏度之间的关系。Mills模型是基于修正光学碱度,结合钢渣和含氟渣的黏度数据,得出熔渣光学碱度和黏度之间的关系。Shu模型是基于Arrhenius公式和熔渣结构理论,结合大量实验数据,得出二元系SiO2-MO和SiO2-Al2O3-MO的黏度模型参数。根据补偿效应,将指前系数(A)和熔渣的黏流活化能(E)建立关系,并将其合理拓展到多元系中。关于补偿效应的详细说明,文献[10]已提过,本文不再进行赘述。李金锡等[7]使用熔渣离子分子共存理论,将Arrhenius公式中的黏流活化能回归成各成分的系数和,其形式上虽与补偿效应类似,但并没有补偿效应的实际意义,因此,其模型参数从一种体系拓展到其他体系中时误差较大,需要对其进行修正。针对Shu模型中的黏度模型参数,除FeO相关体系外,其余体系的模型参数误差值较小。因此,本文旨在结合Shu模型和熔渣离子分子共存理论模型的优势,对现有关于FeO渣系的熔渣模型参数进行修正,以期得到较好的结果。
1 模型建立熔渣结构理论包含熔渣完全离子理论、熔渣完全分子理论以及熔渣离子分子共存理论。桥氧、非桥氧、自由氧及Shu等研究的模型均属于离子理论范畴。然而,现实中熔渣是离子与分子共存的。因此,从物质存在的形式来看,熔渣离子分子共存理论计算得到的数值更接近真实值。
1.1 各成分下的结构单元和作用浓度的计算根据熔渣离子分子共存理论,通过CaO-MgO-SiO2-FeO-Al2O3五元渣系相图以及刘帅等[11]六元渣系相图的活度计算,确定CaO-MgO-SiO2-FeO-Al2O3五元渣系中各结构单元,作出如下假设:
1)熔渣结构单元由简单离子(Ca2+、Mg2+、Fe2+、O2-)、酸性氧化物分子(SiO2)、复杂氧化物分子(2CaO·SiO2、CaO·SiO2)等硅酸盐和铝酸盐组成。
2)简单离子和分子之间处于动态平衡状态,如硅酸盐动态平衡方程式如式(1)和式(2)所列。

|
(1) |

|
(2) |
碱性氧化物完全电离方程式如式(3)所列。
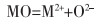
|
(3) |
3)随着熔渣成分的变化,各结构单元处于连续性变化。
4)熔渣内部各组元之间服从质量守恒定律。
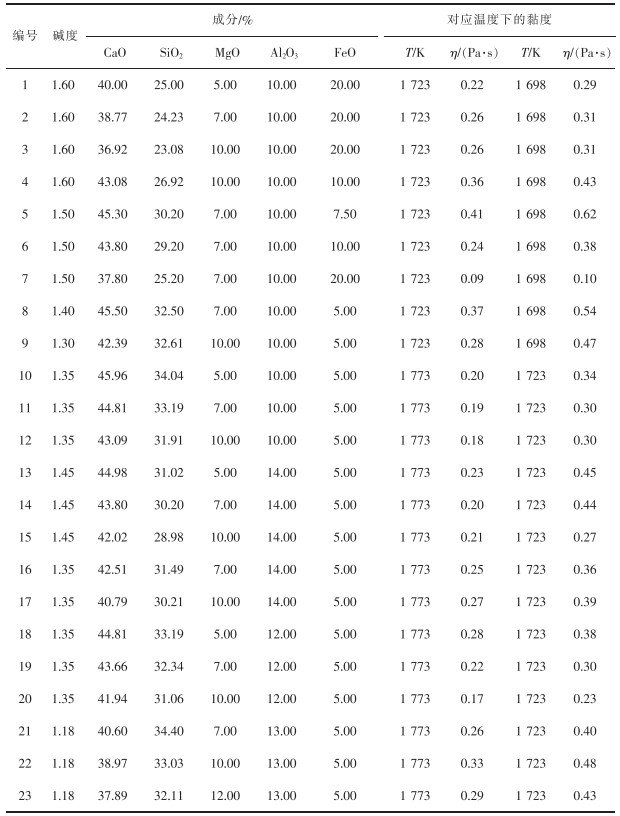
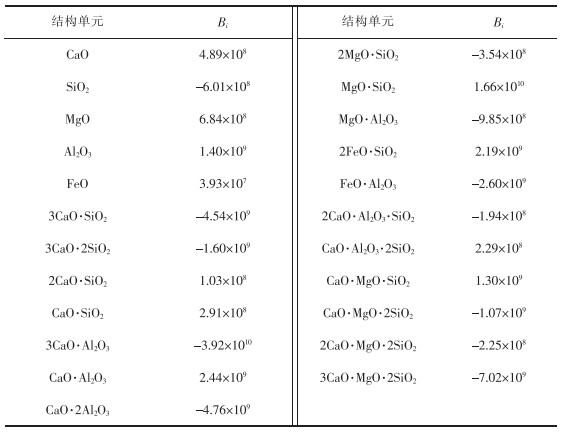
CaO-MgO-SiO2-FeO-Al2O3渣系中所涉及的各结构单元和各反应的标准摩尔吉布斯自由能如表 1所列。
|
|
表 1 CaO-MgO-FeO-Al2O3-SiO2渣系复杂分子反应的化学方程式、吉布斯自由能及质量作用浓度 |
假设渣系总量为100 g,渣中CaO、MgO、SiO2、FeO、Al2O3的物质的量分别用b1~b5表示;平衡时熔渣中各结构单元的质量作用浓度可表示为:N1=N(CaO),N2=N(MgO),N3=N(SiO2),N4=N(FeO),N5=N(Al2O3),Nc1=N(3CaO·SiO2),Nc2=N(3CaO·2SiO2),…,Nc21=N(3CaO·MgO·2SiO2)。离子分子共存理论中使用各结构单元的质量作用浓度代替活度,其表达式如式(4)所列。
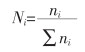
|
(4) |
式(4)中:Ni为熔渣中组元i的结构单元的质量作用浓度;ni为熔渣中组元i的在平衡时的物质的量,mol;ni为假定熔渣为100 g时各结构单元总的物质的量,mol。
根据物料平衡可得式(5)—式(9)。
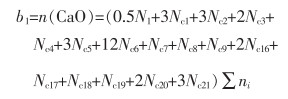
|
(5) |
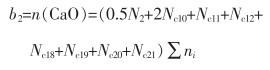
|
(6) |
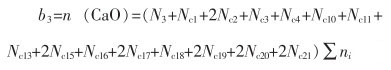
|
(7) |

|
(8) |

|
(9) |
当体系达到平衡时,体系中所有结构单元的质量作用浓度之和为1,其表达式如式(10)所列。
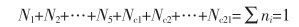
|
(10) |
式(5)—式(9)中存在6个未知量N1、N2、N3、N4、N5、ni,因此,联立式(5)—式(9),通过MATLAB可求解出上述高次非线性方程组。
1.2 含FeO熔渣的黏度数据为了便于确定模型参数,根据文献[12-13],对CaO-SiO2-Al2O3-MgO-5FeO渣系和CaO-SiO2-10Al2O3-MgO-FeO渣系中黏度数据进行拟合,为了确保数据的准确性,需对其黏度数据进行筛选,只选取其中的纯液相黏度数据,剔除可能含有固相的黏度数据,并将本文所使用的黏度数据列入表 2。含Fe熔渣中的铁氧化物的存在形式与“氧势”有关,上述黏度实验在Ar气氛中进行。因此,认为渣中铁氧化物以FeO的形式存在。此外,Shu等[5]在黏度模型拟合过程中也将“FeO”作为网络修饰子,即认为FeO以碱性氧化物的形式存在。故本文中含FeO的熔渣黏度模型拟合过程不考虑Fe3+的存在。
1.3 含FeO熔渣黏度预测模型的建立基于Shu等[5]研究的模型和熔渣离子分子共存理论黏度回归模型,在加入补偿效应后,建立模型。
根据Arrhenius公式,其表达式如式(11)所列。
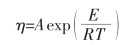
|
(11) |
式(11)中:η为熔渣黏度,Pa·s;A为指前因子;E为黏流活化能,J/mol;R为气体常数,其值为8.314;T为温度,K。
将式(11)两边同时积分可得到式(12)。
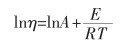
|
(12) |
为了方便计算,将式(12)列为式(13)的形式。

|
(13) |
根据补偿效应,熔渣黏流活化能和指前因子之间存在线性关系,其表达形式如式(14)所列。
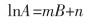
|
(14) |
熔渣黏流活化能表达形式如式(15)所列。
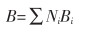
|
(15) |
根据熔渣离子分子共存理论,计算不同温度和成分下各结构单元的质量作用浓度,再根据式(11)—式(15)所列等式,将熔渣黏度实测值和质量作用浓度进行拟合,得到m=-5.786×10-4,n=-1.146。同时,得出各结构单元i的黏流活化能拟合后的数据模型参数如表 3所列。
|
|
表 3 黏度数据回归后各参数值 |
上述结果中,质量作用浓度小于10-10的结构单元,在拟合过程中未进行考虑,其Bi值视为0。因此,基于结构单元回归后得到的B值,其模型值如图 1所示,其相关系数R2为0.997,拟合结果较好。基于补偿效应,熔渣黏流活化能和指前因子呈线性相关,相关系数R2为0.999。根据式(13)得出的斜率和截距,根据式(14)拟合得到m和n值分别为-5.786×10-4和-1.146,具体如图 2所示。根据表 3拟合得到的结果和m、n值,建立熔渣各结构单元的质量作用浓度和黏度之间的关系,其模型拟合值和实测值如图 3所示。经对比发现,模型整体吻合较好,其中模型平均相对误差值为20.30%。由于实验条件的不同,高温黏度模型的误差约为20%,在可接受范围内,因此,模型取得较好的结果。值得一提的是,基于此种方法拟合得到的参数与共存理论拟合得到的参数[12-13]相比,可省去其Ai的参数值而用补偿效应替代。
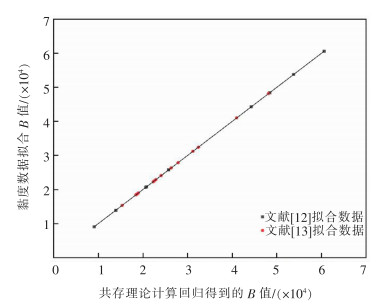 |
| 图 1 共存理论拟合B值和黏度数据回归B值的比较 |
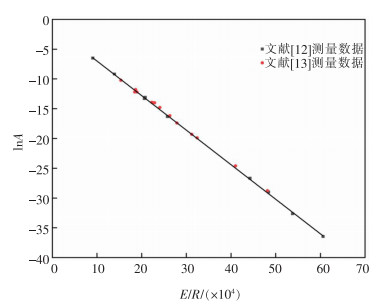 |
| 图 2 lnA与E/R的拟合曲线 |
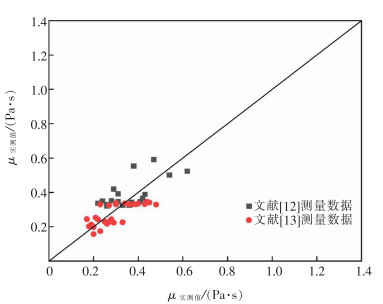 |
| 图 3 黏度实测值与预测值比较 |
FeO质量作用浓度受温度和成分的影响,如图 4(a)—图 4(c)所示。FeO的质量作用浓度随温度变化较小,温度升高,其质量作用浓度略增加,这是由于温度变化时,渣中各物质反应时的吉布斯自由能及化学反应平衡时各物质的量变化均较小,因此,温度对FeO质量作用浓度影响较小。但熔渣组分对渣中FeO的质量作用浓度影响较大。随着熔渣三元碱度(w(CaO)/w(SiO2+Al2O3))和渣中MgO、FeO含量增加,FeO的质量作用浓度增大,其中,FeO的含量对FeO的质量作用浓度影响最大。这是因为渣中碱性氧化物增加,对硅酸盐或铝酸盐的解离作用增加[14],导致整体自由氧O2-含量增加,进而与自由氧O2-结合的Fe2+升高,从而导致渣中FeO的质量作用浓度增加。因此,上述因素均会导致渣中FeO的质量作用浓度升高,通过对比发现,熔渣黏度均随FeO的质量作用浓度增加而减小[15]。
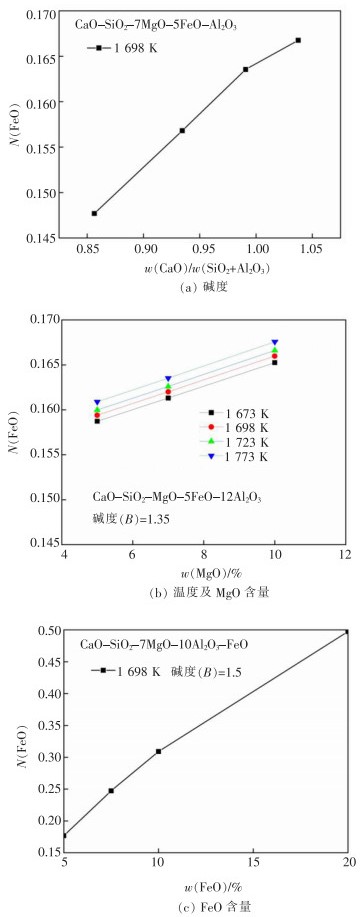 |
| 图 4 FeO质量作用浓度受熔渣三元碱度和渣中MgO、FeO含量的影响 |
通过对上述不同组分之间熔渣黏度的研究发现,熔渣黏度主要与温度和渣中硅酸盐和铝酸盐的聚合作用有关。由图 5(a)—图 5(c)可知,当熔渣成分一定时,温度升高,分子间作用力减小,当分子运动时,内摩擦力减小,熔渣黏度降低。随渣中三元碱度(w(CaO)/w(SiO2+Al2O3))及MgO、FeO含量的增加,熔渣黏度降低[16]。分析表明,随着渣中碱性氧化物增加,渣中自由氧O2-含量增加。熔渣碱度较高时,渣中Al2O3为酸性,SiO2和Al2O3形成硅酸盐和铝酸盐网状结构,为熔渣聚合提供网络形成因子。渣中自由氧O2-含量的增加,促使渣中硅酸盐和铝酸盐网状结构解离,使熔渣聚合度下降,当分子运动时,分子间的剪切应力下降,故熔渣黏度下降。
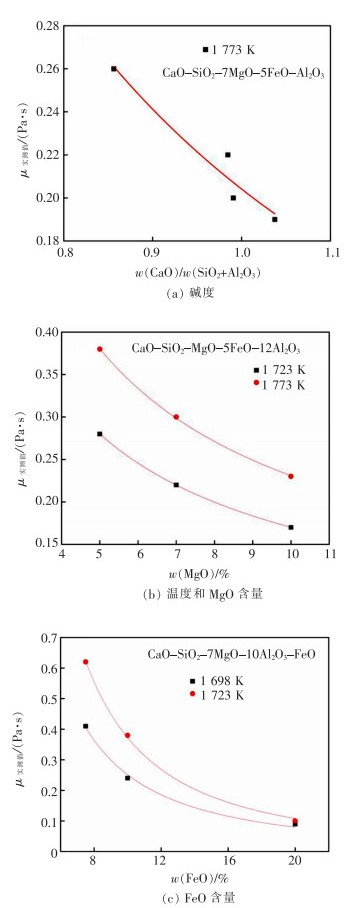 |
| 图 5 熔渣黏度受三元碱度、温度及MgO、FeO含量的影响 |
1)运用熔渣离子分子共存理论,结合前人的实验数据,建立CaO-MgO-SiO2-FeO-Al2O3五元熔渣黏度模型。模型温度范围为1 673~1 773 K,熔渣二元碱度(w(CaO)/w(SiO2))范围为1.18~1.60,FeO含量范围为5%~20%,且为纯液相。经过参数拟合,模型中结构单元和黏流活化能之间的预测值和拟合值较吻合,其相关系数为0.998。基于补偿效应,指前因子lnA和模型预测的熔渣黏流活化能(E)之间呈线性相关,其相关系数为0.999,说明模型中m和n值能反映其线性关系。通过引入补偿效应拟合得到参数m和n的值,在原有理论模型基础上可减少模型参数,使模型计算更为简洁。基于模型参数拟合得到的黏度平均值相对误差为20.30%,说明该模型能大致预测五元渣系CaO-MgO-SiO2-FeO-Al2O3的黏度。
2)熔渣黏度主要受温度和组分的影响。根据熔渣模型计算表明,温度升高,渣中FeO的质量作用浓度增加,但影响较小。与温度相比,渣中组分的变化对FeO质量作用浓度影响较大。随三元碱度(w(CaO)/w(SiO2+Al2O2))和渣中MgO、FeO含量的增加,渣中FeO质量作用浓度增加,其中FeO含量的变化对其影响最大。
| [1] |
郭靖, 程树森, 赵宏博. 基于结构理论的SiO2-CaO-MgO-Al2O3熔渣黏度的预报模型[J]. 钢铁研究学报, 2013, 25(8): 6-11. |
| [2] |
白晨光, 严志明, 庞正德, 等. 炉渣黏度测量与计算模型的研究进展[J]. 钢铁, 2020, 55(8): 27-37. DOI:10.3969/j.issn.1672-5115.2020.08.009 |
| [3] |
RIBOUD P V, ROUX Y, LUCAS L D, et al. Improvement of continuous casting powders[J]. ISIJ International, 1981, 19: 859-869. |
| [4] |
MILLS K C, SRIDHAR S. Viscosities of ironmaking and steelmaking slags[J]. Ironmaking & Steelmaking, 1999, 26(4): 262-268. |
| [5] |
SHU Q F, ZHANG J Y. A semi-empirical model for viscosity estimation of molten slags in CaO-FeO-MgO-MnO-SiO2 systems[J]. ISIJ International, 2006, 46(11): 1548-1553. DOI:10.2355/isijinternational.46.1548 |
| [6] |
SHU Q F. A Viscosity estimation model for molten slags in Al2O3-CaO-MgO-SiO2 System[J]. Steel Research International, 2009, 80(2): 107-113. |
| [7] |
李金锡, 张鉴. CaO-MgO-CaF2-Al2O3-SiO2五元渣系粘度的计算模型[J]. 北京科技大学学报, 2000, 22(4): 316-319. DOI:10.3321/j.issn:1001-053X.2000.04.008 |
| [8] |
张康晖, 张延玲, 李秋寒, 等. 基于共存理论的含铬渣黏度预测模型[J]. 钢铁研究学报, 2019, 31(3): 251-257. |
| [9] |
URBAIN G. Viscosity estimation of slags[J]. Steel Research, 1987, 58(3): 111-116. DOI:10.1002/srin.198701513 |
| [10] |
DOSDALE T, BROOK R J. Cationic conduction and diffusion and the compensation law[J]. Journal of Materials Science, 1978, 13(1): 167-172. DOI:10.1007/BF00739287 |
| [11] |
刘帅, 鲁浩, 郭汉杰, 等. 电渣重熔六元渣系FeO活度的研究[J]. 材料与冶金学报, 2017, 16(1): 30-37. |
| [12] |
KIM J R, LEE Y S, MIN D J, et al. Influence of MgO and Al2O3 contents on viscosity of blast furnace type slags containing FeO[J]. ISIJ International, 2004, 44(8): 1291-1297. DOI:10.2355/isijinternational.44.1291 |
| [13] |
LEE Y S, MIN D J, JUNG S M, et al. Influence of basicity and FeO content on viscosity of blast furnace type slags containing FeO[J]. ISIJ International, 2004, 44(8): 1283-1290. DOI:10.2355/isijinternational.44.1283 |
| [14] |
SHEN X, CHEN M, WANG N, et al. Viscosity property and melt structure of CaO-MgO-SiO2-Al2O3-FeO slag system[J]. ISIJ International, 2019, 59(1): 9-15. DOI:10.2355/isijinternational.ISIJINT-2018-479 |
| [15] |
YAN Z M, REDDY R G, LV X W, et al. Viscosity of iron oxide aluminosilicate melts[J]. Metallurgical and Materials Transactions B, 2019, 50(1): 251-261. DOI:10.1007/s11663-018-1460-z |
| [16] |
YAN Z M, REDDY R G, LV X W. Structure based viscosity model for aluminosilicate slag[J]. ISIJ International, 2019, 59(6): 1018-1026. DOI:10.2355/isijinternational.ISIJINT-2018-724 |
 2023, Vol. 43
2023, Vol. 43