| 基于三元闭包的不确定图差分隐私保护算法 |
随着互联网技术的飞速发展,全世界的用户都在使用社交网络平台共享信息与他人建立联系[1-2]。社交网络平台积累了大量的用户数据,其中,个人敏感信息易成为不法分子攻击的目标。因此,如何保护好用户个人敏感信息成为亟需解决的安全问题。
社交网络中用户之间的关系错综复杂,为了准确描述用户之间的关系,可以将社交网络转化成图,顶点代表用户,顶点之间的边代表用户之间的关系[3]。因此,对社交网络的隐私保护研究可以转化为对社交网络图的隐私保护研究。不确定图法是一种社交网络图的隐私保护方法,通过给原始社交网络图中较新的部分边赋予存在概率来达到整个图的不确定性,从而实现隐私保护。Boldi等首次提出在社交网络的隐私保护中,将不确定性注入社交网络,将生成的不确定图公之于众。他们提出了混淆算法,该算法通过更细微的扰动来添加或删除部分社交网络图中的边,实现相同的混淆水平,从而保持更高的效用[4]。但混淆算法的不确定预算取最小值时,若抽样边存在社交网络图中,则该抽样边的存在概率接近1,否则存在概率接近0,因此攻击者可以通过取舍技术还原出原始社交网络图。Nguyen等针对基于不确定性的匿名化方案存在的缺陷,提出一种在隐私保护性和数据可用性之间提供更好权衡的新方法——最大方差法。该方法首先将原始社交网络图分割成若干个子图,然后给每个子图中注入不确定性,最后将所有子图通过合成的方式生成新的社交网络图[5]。虽然最大方差使社交网络图中节点的总度数保持不变,但在图分割的过程中造成了边的遗失,对图的结构造成了较大的破坏。Nguyen等在前期工作的基础上,提出了一种基于不确定邻接矩阵的通用模糊模型,使期望节点度与未匿名化图中的期望节点度相等,并且利用不确定性概念开发了一个度量节点识别其他风险的框架,但该通用模糊模型存在无法抵御背景知识攻击的问题[6]。吴振强等针对社交网络中用户之间关系遭到泄露的问题,在不确定图法的基础上结合三元闭包原理,提出了三元闭包算法。三元闭包算法对原始数据图利用三元闭包原理进行加边形成三角形,然后对三角形的边赋予随机的概率值,实现对社交网络图的隐私保护[7]。虽然三元闭包算法实现了对社交网络的隐私保护,但这种隐私保护无法提供可控的隐私级别,而且无法抵御背景知识攻击。
综上所述,不确定图法存在无法通过数学理论严格证明其隐私保护强度和对数据的保护程度依赖攻击者拥有的背景知识两大弊端,导致处理结果的可靠性大大降低。为了解决三元闭包算法中存在的弊端,结合差分隐私技术[8],提出了基于三元闭包的不确定图差分隐私保护算法(Ternary Closure and Differential Privacy,TCDP)。TCDP算法用符合拉普拉斯分布的随机数代替三元闭包算法中简单的随机数,使算法满足差分隐私,在提高算法隐私保护性的同时,还提供可控的隐私级别和抵御攻击者拥有最大背景知识条件下的攻击。
1 基础知识 1.1 差分隐私差分隐私是由Dwork等在2006年针对数据库数据隐私保护的问题提出的一种新型隐私保护模型,该模型将随机噪声注入真实数据集中进行扰乱,达到隐私保护的效果,并且使数据的整体属性保持不变,扰乱后的数据仍可用于数据挖掘等操作[9]。差分隐私具有严格的数学理论证明,向数据集中添加或者删除任意一条数据都不会影响查询结果,且能抵御攻击者拥有最大背景知识条件下的攻击。下面给出差分隐私应用在社交网络图中的相关定义:
定义1 邻近数据集[9]:对于两个数据集D和D′,若D和D′仅相差一条数据记录,则称D和D′互为邻近数据集。
定义2 ε-差分隐私[9]:给定一个随机查询算法F,对于任意邻近数据集D和D′,若F在数据集D和D′查询下得到的结果满足式(1),则称随机查询函数F满足ε-差分隐私。
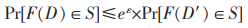
|
(1) |
其中, Pr[·]表示若应用随机查询算法F数据可能被泄露的风险;ε表示随机查询算法F所能够提供的隐私保护水平。
相比于数据库中的相邻数据集,社交网络中则有邻近图的定义。
定义3 邻近图[10]:给定图G1=(V1,E1),G2=(V2,E2),若存在(V1⊕V2)+(E1⊕E2)=1,则称G1,G2为邻近图。
定义4 边差分隐私[10]:给定一个随机算法A,Range(A)是算法A的取值范围,若算法A在邻近图G1,G2上的输出结果S(S∈Range(A))满足式(2),则称算法A满足ε-边差分隐私。
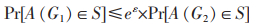
|
(2) |
边差分隐私保护边的隐私信息不被泄露,从而保护顶点之间的关联。故在边差分隐私算法中邻近图G1,G2中V1=V2,E1⊕E2=1。
定义5 敏感度:图G1,G2是邻近图,假设Δf是查询函数f的敏感度,则:
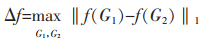
|
(3) |
定义6 Laplace机制:对于给定数据集D,有查询函数f: D→Rd,若算法A的输出结果满足式(4),则称算法A满足ε-差分隐私。
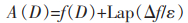
|
(4) |
其中,Δf是查询函数的敏感度;ε为隐私预算。
1.2 社交网络图社交网络包括用户以及用户之间的关系,通常用图来表示。图 1是一个简单的社交网络图,其中顶点表示用户,边表示图中两个用户之间的关系。
 |
| 图 1 社交网络图 |
定义7 不确定图[4]:给定一个图G=(V,E),存在映射p: V2→[0, 1],表示边集中每条边存在的概率,那么G′=(V,p)表示图G的不确定图。
其中,V2={(vi,vj)|1≤i≤j≤n},表示顶点集合V中所有的顶点对。
1.4 三元闭包三元闭包(Ternary Closure)是网络中一种重要的链接延伸机制,其本身是一种非常直观和自然的描述[11],其定义如下:
定义8 三元闭包[11]: 在社交网络中,由A、B、C 3个节点所组成的三元组,若A-B和A-C之间存在关系,则B-C在未来存在关系的可能性就会提高。
针对图 1中的社交网络,节点B和节点E有共同的朋友A,则B和E成为朋友的概率会增加;同理,节点B和节点E也会产生关联边。根据三元闭包原理,图 1中的社交网络可以转变成图 2的不确定图,其中实线代表原始网络,虚线代表添加的联动边。
 |
| 图 2 三元闭包理论模型 |
信息熵[12]是用来度量一个系统信息含量的量化指标,信息熵越高,则系统越混乱;反之,则系统越有序。由于不确定图的边具有随机性,引用边熵(Ente)来度量算法的隐私保护效果。
定义9 边熵[13]:描述系统的混乱程度,系统越不稳定,边熵值越大。边熵的计算公式如下:
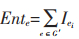
|
(5) |
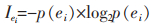
|
(6) |
其中,ei∈G′,p(ei)是该边存在的概率。
1.6 数据可用性度量指标Boldi等将不确定图应用在社交网络的同时,为了证明不确定图在特征性质方面与原图高度相似,提出了一些基于统计数据的数据可用性度量指标[4],如边数(Number of Edges,NE)和节点平均度(Average Degree,AD)等。下面给出边数和节点平均度的计算方式。
令图G的度序列为d1,…,dn,顶点对为v2={(vi,vj)|1≤i≤j≤n},边为e。对于函数F,若存在S=F(d1,…,dn),则称S是基于度的统计。
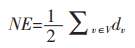
|
(7) |
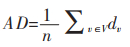
|
(8) |
当G′是一个不确定图时,d1,…,dn是随机变量。如果函数F是线性函数,则有:
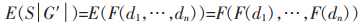
|
(9) |
因此,顶点v∈V的期望度等于其邻近边的概率之和,则有:
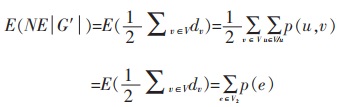
|
(10) |
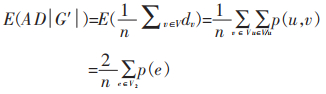
|
(11) |
三元闭包算法是吴振强等针对社交网络中用户之间关系遭到泄露的问题提出的一种不确定图算法[7]。相比于其他的不确定图算法,三元闭包算法有两个优势,首先,三元闭包算法利用三元闭包原理对原始社交网络图进行加边后,再注入不确定性,可以保留更多原始图的结构;其次,三元闭包算法对图中三角形注入的不确定性加以限制,设三角形3条边存在概率之和为2,使得生成图边数的期望与原始图一致。但是,三元闭包算法注入的不确定性是简单的随机噪声,只能通过控制三角形的个数来控制算法提供的隐私保护性。在实际应用中,当三角形的数量较少时,会出现只有局部的社交网络发生了变化,大部分的社交网络和原社交网络一致的现象,这就会导致两种结果:
1)没经过扰动的社交网络中用户的隐私会被泄露。
2)当攻击者拥有足够的背景知识,经过扰动的局部社交网络容易被攻击者攻破,造成隐私泄露。
不少学者将差分隐私应用在社交网络的隐私保护中[14],为本文解决三元闭包存在的问题提供了思路。因为直接将差分隐私应用在社交网络图中会加入过大的噪声,导致图的结构遭到较大破坏,所以,本文提出的TCDP算法保留了三元闭包算法中利用三元闭包原理对原始社交网络图进行加边的过程。TCDP算法用符合拉普拉斯分布的随机值代替三元闭包算法中简单的随机值,使算法满足差分隐私,通过控制隐私预算控制算法的隐私保护性。TCDP算法因为满足差分隐私,所以可以抵御背景知识攻击。
TCDP算法首先遍历原始社交网络图的顶点对,根据三元闭包原理对满足顶点之间最短路径为2的顶点对进行加边(默认边的权重为1),所添加的边与最短路径的两条边形成三角形,并记录到三角形集中,结束遍历后,将社交网络图中不属于三角形集的边添加到确定边集中;然后对三角形集的边添加符合拉普拉斯分布的存在概率,对确定边集中的边赋予存在概率为1;最后根据社交网络图中每条边存在的概率生成新的社交网络图。
2.2 算法流程TCDP算法的整体目标是:假定在攻击者拥有最大背景知识的情况下,保护社交网络中用户之间敏感边的信息不被泄露。给定一个无向社交网络,发布一个满足差分隐私的扰动网络,并且尽可能地保留原始社交网络的结构特性。TCDP算法的流程如图 3所示。
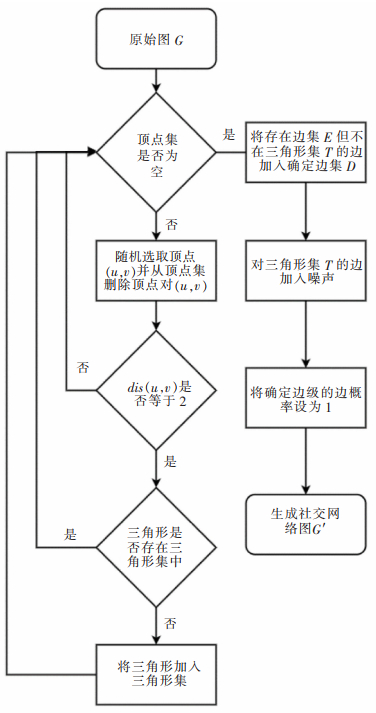 |
| 图 3 TCDP算法流程 |
从图 3可知,TCDP算法大致可以分为以下6个步骤:
1)判断顶点对集合V2是否为空,如果为空,则进行步骤4;如果不为空,则进行下一步。
2)从顶点对集合V2中,随机选取顶点对(u,v),并将该顶点对(u,v)从顶点对集V2中删除。
3)判断边(u,v)是否为社交网络图的边,若是,则跳过;若不是,则寻找是否存在一个点i使得顶点对(u,v)最短路径为2,即dis(u,v)=2。若点存在且三角形T(u,v,i)中的边不存在三角形集T中,则将三角形T(u,v,i)添加到三角形集T中,将边(u,v)添加到社交网络图的边集E中;否则回到步骤1。
4)将存在边集E中但不存在三角形集T的边添加到确定边集D中,即D{e|e∈E,e∉T}。
5)对三角形集T中每个三角形的边赋予符合拉普拉斯分布的存在概率,对确定边集D的边赋予1的存在概率。
6)根据社交网络图中边的存在概率重新生成社交网络图。
2.3 算法伪代码输入:原图G=(V,EG),顶点对集合V2,三角形集合T和确定边集D
输出:不确定图G′(V,p)
1. S←Ø,T←Ø
2. While |V2|> 0 do:
3. 随机选取顶点对(u,v),V2←V2-(u,v)
4. if(u,v)∉EG,dis(u,v)=2:
5. if T(u,v)∩T=Ø:
6. EG←EG∪(u,v)
7. T←T∪(u,v)
8. D←D{e|e∈E,e∉T}
9. for e in T :
10. 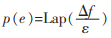
11. for e in D:
12. p(e)=1
13. Return G′(V,p)
将原始社交网络图G=(V,EG)转换成TCDP算法处理后的不确定图G′(V,p),需要经历以下6个步骤:①创建三角形集和确定边集并对其初始化,如算法第1行所列。②对顶点对集进行遍历,根据三元闭包原理对满足两个顶点之间最短路径为2的顶点对进行加边(默认边的权重为1),与最短路径的两条边形成三角形,并将对应的三条边记录到三角形集中,如算法第3-7行所列。③在遍历结束后将社交网络图中不属于三角形集的边添加到确定边集中,如算法第8行所列。④对三角形集的边添加符合拉普拉斯分布的存在概率,如算法第9-10行所列。⑤对确定边集的边赋予存在的概率为1,如算法第11-12行所列。⑥根据社交网络图中每条边存在的概率生成新的社交网络图G′(V,p),如算法第13行所列。
2.4 算法差分隐私保证TCDP算法分为两部分:第一部分为算法查询函数,如算法伪代码中第2-8行所列;第二部分为添加噪声,如算法伪代码中第9-12行所列。
TCDP算法是基于边的差分隐私保护算法,假设图G1(V1,E1)和图G2(V2,E2)为TCDP算法中的邻近图,则根据定义4有V1=V2以及E1⊕E2=1。假设图G1和图G2相差的边为e,则有E1=E2∪e。根据算法流程图,令图G1(V1,E1)进行到步骤4时所生成的三角形集为T1,边集为E1′;图G2(V2,E2)进行到步骤4时所生成的三角形集为T2,边集为E2′。
下面对图G2(V2,E2)中的边e是否存在点i使得与边e相邻的一条边形成三角形而加入到T2中进行假设分析,令边e由顶点对(a,b)组成:
1)假设存在点i使得dis(a,b)=2,且形成的三角形T(a,b,i)中的边不存在于三角形集T2中,则有,T1⊕T2=1,E1′⊕E2′=2。
2)假设存在点i使得dis(a,b)=2,但形成的三角形T(a,b,i)中某条边存在于三角形集T2中,则有,T1⊕T2=0,E1′⊕E2′=1。
3)假设不存在点i使得dis(a,b)=2,则有,T1⊕T2=0,E1′⊕E2′=1。
综上所述,由边e所造成图G1(V1,E1)和图G2(V2,E2)中E1′和E2′最大差值为2,由定义5可得:
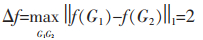
|
(12) |
根据定义6,在Laplace机制中,查询函数f所添加的Laplace噪声为Lap(Δf/ε),其中Δf=2,则TCDP算法提供ε-边差分隐私保护。算法的隐私保护程度由隐私预算ε决定,隐私预算ε越大,噪声的取值范围越窄,算法的隐私保护效果越差;反之隐私预算ε越小,噪声的取值范围越广,算法的隐私保护效果越好。
2.5 算法时间复杂度分析根据三元闭包原理对原始图加边的过程中,假设原始图有n条边,m条不存在边集的边,则加边过程的时间复杂度为O(n×m);假设在加边过程中添加了i条边,则添加噪声总的时间复杂度为O(n+i),因此,TCDP算法的时间复杂度为O(n×m)。
3 实验设计与结果分析 3.1 实验环境与实验设计硬件环境:Intel(R)Xeon(R)CPU E5-2680 v3 @ 2.50 GHz;2.32 GB内存,1 TB硬盘。
软件环境:Windows 10,64位操作系统;Python3。
实验数据集信息:
实验数据采用了真实数据集和合成数据集,真实数据集源自karate俱乐部和Dolphin社会网络,合成数据集分别为200和500个节点、连接概率为0.2的随机网络图。
为了对TCDP算法和三元闭包算法的隐私保护性进行对比分析,设计了一个基于信息熵的实验,通过计算TCDP算法在不同隐私预算(ε=0.3,0.5,0.7,0.9)下的信息熵与三元闭包算法在不同的调节边数因子(c=0.3,0.5,0.7,1)下的信息熵进行对比分析,从而判断算法隐私保护性的优劣。为了对TCDP算法和三元闭包算法的数据可用性进行对比分析,设计了一个基于统计数据的实验,通过计算TCDP算法在不同隐私预算(ε=0.3,0.5,0.7,0.9)与三元闭包算法在不同的调节边数因子(c=0.3,0.5,0.7,1)的情况下,统计图中边数和节点平均度进行对比分析,从而判断算法数据可用性的优劣。为了对TCDP算法性能进行分析,设计了基于图密度的实验,通过记录TCDP算法在不同连接概率(p=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9)的200个节点和500个节点的随机网络图下的运行时间,从而分析图密度对算法性能的影响。
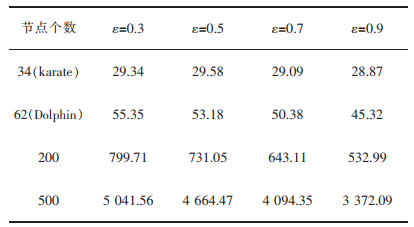
3.2 算法隐私保护性分析实验为了对本文所提出的TCDP算法和三元闭包算法的隐私性作统一的度量,引用信息熵中的边熵来衡量算法的隐私效果,以此为评价依据衡量隐私预算变化所带来算法隐私程度的变化。由于不确定图具有不确定性,所以算法的边熵值越大,生成的不确定图的不确定程度也越大。表 1为TCDP算法在不同隐私预算下边熵值的变化情况,表 2为三元闭包算法在不同调节边数因子下边熵值的变化情况。
|
|
表 1 TCDP算法中边熵的变化情况 |
|
|
表 2 三元闭包算法中边熵的变化情况 |
由于TCDP算法满足差分隐私,根据差分隐私的性质,由差分隐私预算控制算法的隐私保护水平,其值越小隐私保护水平越高。分析表 1数据可知,在相同数据集中,随着ε减小,算法提供的隐私保护水平不断提高,算法的边熵值在不断增加。在节点较少的Dolphin社交网络中,算法的边熵值在不同ε之间相差不大;随着节点个数的增加,从200个节点的随机网络图到500个节点的随机网络图时,算法边熵值的增长幅度越来越大,说明算法提供的隐私保护性随着节点数的增加而显得更加明显。
三元闭包算法通过控制添加噪声的三角形数量来控制算法整体的隐私保护性,假设在社交网络中,三元闭包算法通过三元闭包原理最多添加了m个三角形,设置一个调节因子控制三角形数量,则实际添加噪声的三角形数量为m×c。分析表 2数据可知,在相同数据集中,随着调节因子c不断减少,所添加噪声的三角形数量不断较少,边熵值也在不断减少,且幅度较为明显。
对比表 1和表 2发现,在社交网络图节点较少的karate数据集和Dolphin数据集中,TCDP算法和三元闭包算法的边熵值较为相近,说明TCDP算法和三元闭包算法在节点较少的社交网络中隐私保护性相近;随着节点个数增加,TCDP算法的边熵值与三元闭包算法的边熵值的差距也随之增加,说明社交网络中用户较多时,TCDP算法的隐私保护性更高。实验结果表明,整体上TCDP算法在隐私保护程度上优于三元闭包算法,具有较好的隐私保护效果。
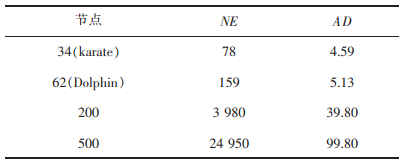
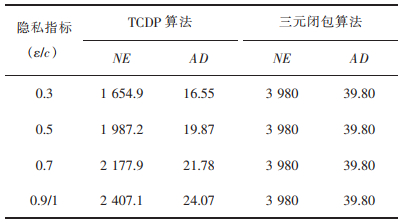
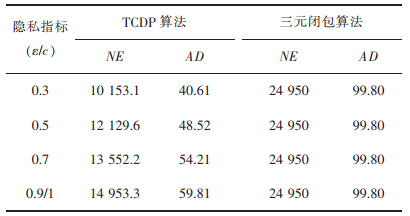
3.3 算法数据可用性分析实验在数据可用性分析的实验中,使用Boldi等提出的NE、AD来度量算法的数据可用性。实验数据见表 3-表 7,其中,表 3为原始图的数据可用性指标;表 4-表 7分别为TCDP算法和三元闭包算法在karate俱乐部数据集、Dolphin社会网络数据集及200、500个节点连接概率为0.2的随机网络图上的实验数据。
|
|
表 3 原始图数据的数据可用性指标 |
|
|
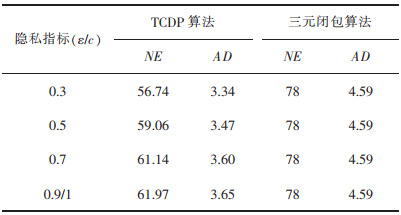
表 4 算法在karate俱乐部数据集图的数据可用性 |
|
|
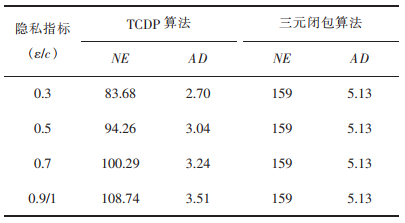
表 5 算法在Dolphin社会网络数据集图的数据可用性 |
|
|
表 6 算法在200个节点随机网络图的数据可用性 |
|
|
表 7 算法在500个节点随机网络图的数据可用性 |
在不确定图中,NE和AD分别代表图中边个数和节点平均度的期望。对比表 4-表 7,三元闭包算法因为每个三角形的总概率值为2,NE和AD值不会随着c而改变,具有很高的数据可用性。对比表 3和表 4,当社交网络图中顶点数量较少时,TCDP算法的NE和AD值约为原始图的72%~79%,保留了原始图72%~79%的边个数和节点平均度。随着节点个数不断增加,TCDP算法的NE和AD值占原始图的比例不断减少,说明TCDP算法的数据可用性随着社交网络图的节点数量增加而减少。当社交网络图的节点个数达到500个,约保留了原始图60%的边个数和节点平均度。
实验结果表明,三元闭包算法在数据可用性方面优于TCDP算法。在小型社交网络图中,TCDP算法具有较高的数据可用性;随着用户不断增加,直至500个用户,TCDP算法的数据可用性一般。
3.4 算法性能分析实验通过记录TCDP算法在不同连接概率(p=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9)的200个节点和500个节点的随机网络图下的运行时间,从而分析图密度对算法性能的影响。实验数据见图 4,其中,图 4(a)为TCDP算法在具有200个节点不同连接概率下随机网络图的运行时间,图 4(b)为TCDP算法在具有500个节点不同连接概率下随机网络图的运行时间。
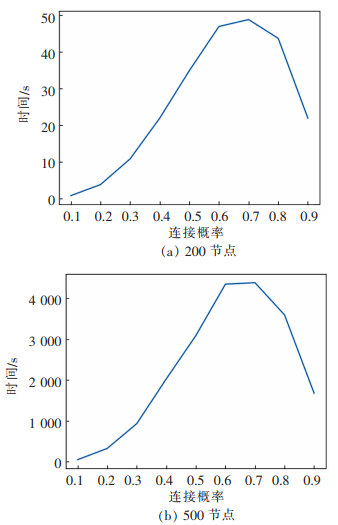 |
| 图 4 TCDP算法不同连接概率随机网络图的运行时间 |
随机网络图的连接概率决定了生成图密度。假设n代表图中边的个数,m代表不存在边集的边的个数,分析图 4的数据可知,在连接概率较小(p=0.1,0.2)的随机网络图中,m≫n,虽然图中有很多条空边,但是图中的边太少,满足三元闭包原理的边数较少,TCDP算法整体运行时间较短;随着连接概率不断增加,TCDP算法的运行时间不断增加,在连接概率p=0.7时达到最大值;在连接概率较大(p=0.8,0.9)的随机网络图中,n≫m,虽然图中的边数较多,但是空边的数量较短,满足三元闭包原理的边数较少,TCDP算法的运行时间比在连接概率p=0.7的随机网络图的运行时间少。实验结果表明,TCDP算法的性能受图密度的影响,在稀疏图中,算法的运行时间先随着图密度的增加而增加,到达一个峰值后,又将逐渐减少。
4 结论本文提出了基于三元闭包的不确定图差分隐私算法, 该算法结合了差分隐私和三元闭包原理,将Laplace噪声添加到社交网络图中的边,用于保护社交网络中用户之间的关系。实验证明,TCDP算法比三元闭包算法具有更高的隐私保护性,且保持着不错的数据可用性,适用于需要高隐私保护的场景。在未来的工作中,我们将着手提高TCDP算法在大型社交网络中的数据可用性。
| [1] |
NETTLETON D F, ESTIVILL-CASTRO V, SALAS J. Privacy in multiple on-line social networks-Re-identification and predictability[J]. Transactions on Data Privacy, 2019, 12(1): 29-56. |
| [2] |
吴小龙, 张丽丽. 大数据视角下高校思想政治理论教育创新[J]. 江西理工大学学报, 2017, 38(4): 20-23. |
| [3] |
刘向宇, 王斌, 杨晓春. 社会网络数据发布隐私保护技术综述[J]. 软件学报, 2014, 25(3): 576-590. |
| [4] |
BOLDI P, BONCHI F, GIONIS A, et al. Injecting uncertainty in graphs for identity obfuscation[J]. Proceedings of the VLDB Endowment, 2012, 5(11): 1376-1387. DOI:10.14778/2350229.2350254 |
| [5] |
NGUYEN H H, IMINE A, RUSINOWITCH M. A maximum variance approach for graph anonymization[C]//International Symposium on Foundations and Practice of Security. Springer, Cham, 2014: 49-64.
|
| [6] |
NGUYEN H H, IMINE A, RUSINOWITCH M. Anonymizing social graphs via uncertainty semantics[C]//Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security. Singapore Republic of Singapore. New York, USA: ACM, 2015: 495-506.
|
| [7] |
吴振强, 胡静, 田堉攀, 等. 社交网络下的不确定图隐私保护算法[J]. 软件学报, 2019, 30(4): 1106-1120. |
| [8] |
KARWA V, RASKHODNIKOVA S, SMITH A, et al. Private analysis of graph structure[J]. ACM Transactions on Database Systems, 2014, 39(3): 1-33. |
| [9] |
DWORK C. Differential privacy[M]. Automata, Languages and Programming. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006: 1-12.
|
| [10] |
HAY M, LI C, MIKLAU G, et al. Accurate estimation of the degree distribution of private networks[C]//2009 Ninth IEEE International Conference on Data Mining. IEEE, 2009: 169-178.
|
| [11] |
EASLEY D, KLEINBERG J. Networks, crowds, and markets[M]. Cambridge: Cambridge University Press, 2010.
|
| [12] |
刘明, 华亮. 基于PSOOI算法的PID控制器参数整定[J]. 控制工程, 2016, 23(1): 64-68. |
| [13] |
LEWIS T G. Network science: Theory and applications[M]. New Jersey John Wiley & Sons, 2011.
|
| [14] |
TASK C, CLIFTON C. A guide to differential privacy theory in social network analysis[C]//2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. IEEE, 2012: 411-417.
|
 2022, Vol. 42
2022, Vol. 42