| 多级数CBEF-Ritz法在高阶剪切变形梁非线性弯曲分析中的应用 |
梁在工程中有着广泛的应用,且对梁的大挠度分析具有重要的实际意义。因此,大量的分析方法,如摄动法[1]、打靶法[2]、最小残差法[3]、变分微分求积法[4]、积分法[5]、龙格-库塔法[6]、有限差分法[7]、有限元法[8-10]、边界元法[11]等都被用于计算分析集中荷载或分布荷载作用下梁的大挠度问题。
梁结构分析中的几何非线性和材料非线性问题一直是许多学者研究的课题。对工程结构进行非线性分析,可以有效模拟结构在不同荷载作用下的响应全过程,进而深入掌握结构的受力特点,为结构性能评估提供有效手段。近年来,Solano-Carrillo提出了Ludwick型材料悬臂梁在自由端垂直集中力和均布荷载共同作用下大挠度的半解析解[12]。Borboni等讨论了非线弹性非对称Ludwick悬臂梁在自由端受水平力、垂直力和弯曲力矩作用下的大挠度行为[13]。Vaz等利用摄动理论研究了线性黏弹性悬臂梁在简谐集中荷载作用下的准静态响应[1]。Ansari等利用变分微分求积方法研究了三阶剪切变形功能梯度微梁的尺寸相关非线性力学行为[4]。Shvartsman采用直接法对柔性非均匀悬臂梁在端部集中随动力作用下进行了静力分析[14]。Humer给出了集中力作用下可伸缩弹性梁的椭圆积分解[15]。Li等研究了三点弯曲下摩擦端支承Timoshenko梁的大挠度和转动[16]。Kasirajan等利用非线性有限元方法研究了Timoshenko梁非线性力学行为的表面效应和非局部效应[9]。Nguyen等采用有限元方法研究了非均匀分布荷载作用下弹塑性功能梯度陶瓷-金属梁的非线性弯曲问题[10]。Su等建立了有限元模型,并对铝合金实心空心型材在集中横向荷载作用下的实验结果进行了验证[17]。Wang等对国产316不锈钢的荷载-挠度关系进行了实验研究,发现实验挠度大于计算结果[18]。Razzaq等采用实验和理论两种方法研究了简支热塑性梁在逐渐增大的跨中集中荷载作用下的弯曲性能[7]。Yang等提供了关于预拉应力LWC梁弯曲性能的试验数据,并与多种经验非线性模型的预测结果进行了比较[19]。毛丽娟等用直接求解法给出了剪切可变形梁非线性静态响应的精确解[20]。张旭等提出一种求解几何非线性问题的优化算法,并研究了简支梁的几何非线性大变形问题[21]。
诸多学者针对结构非线性分析的特点提出了高效求解方法,但每种方法均有各自的适用性和局限性。如精确解析解虽然精确,但是对结构的边界或荷载有着特殊的要求,能得到的解析解答非常有限;对于某些强非线性问题,摄动法解答的适用域可能有一定的局限;有限元法是最常用的结构非线性分析方法,但随着分析模型精细化程度的提高,有限元分析会耗费大量的计算资源。由于非线性分析过程的复杂性,寻求高效的非线性分析方法仍是解决该问题的根本途径。因此,充分认识非线性分析方法的计算性能,找到适用于不同求解问题的高效算法,仍是结构非线性分析的研究重点。本文首次提出了用于高阶剪切变形梁非线性分析的多级数经典梁本征函数Ritz方法,并研究了集中荷载作用下双参数弹性地基(Pasternak型)梁的非线性弯曲性能。最后,详细讨论了不同支承端、弹性地基、长厚比和集中荷载对梁非线性弯曲响应的影响。
1 高阶剪切变形梁基本方程厚度为h和长度为Lx的矩形截面梁,如图 1所示。假定地基的荷载-位移关系是p=K1w-K2d2w/dx2,其中,p是单位面积的力;K1是Winkler地基刚度;K2表示剪切影响系数。
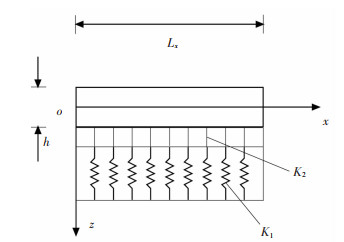 |
| 图 1 双参数弹性地基梁的几何与坐标 |
高阶剪切变形梁理论[22]的位移场可以假定为以下形式:
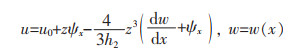
|
(1) |
式(1)中:u与w是总体位移;u0是x方向上的中面位移;ψx是法线围绕y轴的旋转量。考虑非线性von Kármán应变-位移关系,应变可表示为:
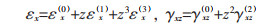
|
(2) |
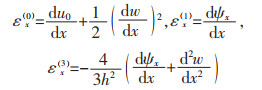
|
(3a) |
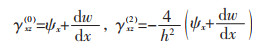
|
(3b) |
式(2)中:εx与γxz分别是正应变和剪应变;式(3)中:εx(i)与γxz(j)(i=0,1,3和j=0,2)分别是正应变和剪应变的分量。值得注意的是γxz在上表面(z=-h/2)和下表面为0。根据胡克定律,应力可以确定为:
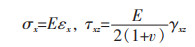
|
(4) |
通过适当的积分可以导出本构方程,
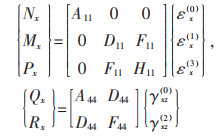
|
(5) |
式(5)中:梁的各阶刚度定义如下:
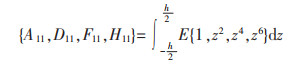
|
(6a) |
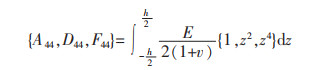
|
(6b) |
根据能量变分原理导出平衡方程:
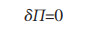
|
(7) |
式(7)中: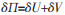
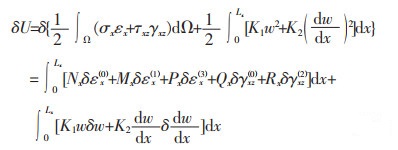
|
(8a) |
式(8a)中:Ω表示梁的域。外力所做的虚功为:
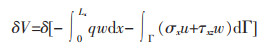
|
(8b) |
式(8b)中:Γ表示梁的端部。平衡方程可以表示为:
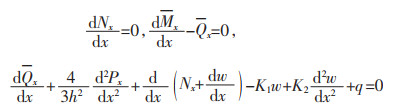
|
(9) |
式(9)中:
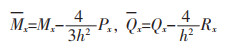
|
(10) |
控制方程可以通过式(5)与式(9)简化:
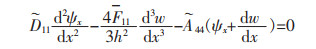
|
(11a) |
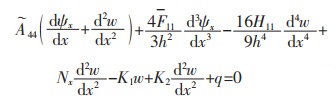
|
(11b) |
式(11)中:
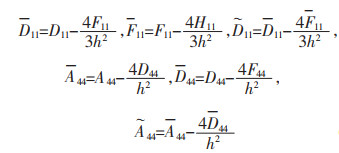
|
(12) |
假定梁的端部在中面上没有平面内位移,则Nx可以用积分形式写成:
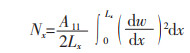
|
(13) |
在下面的分析中,将考虑端部边界条件的3种情况:
1)两端简支且无面内位移,简记为SS。

|
(14a) |
2)两端被固定夹紧且无面内位移,简记为CC。
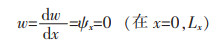
|
(14b) |
3)一端被固定夹紧另一端简支且无面内位移,简记为CS。
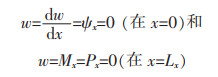
|
(14c) |
采用经典梁本征函数(Classical Beam Eigen-Functions,简写CBEF)和多级数Ritz方法获得梁的非线性弯曲响应的近似解,可以假设:
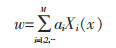
|
(15) |
式(15)中:M为级数总数;ai为待定系数;Xi(x)为第i阶经典梁本征函数。对于具有SS边界条件的梁:
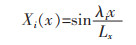
|
(16a) |
对于具有CC边界条件的梁:
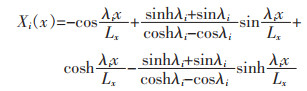
|
(16b) |
对于具有CS边界条件的梁:
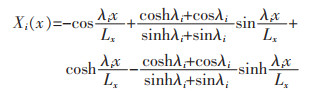
|
(16c) |
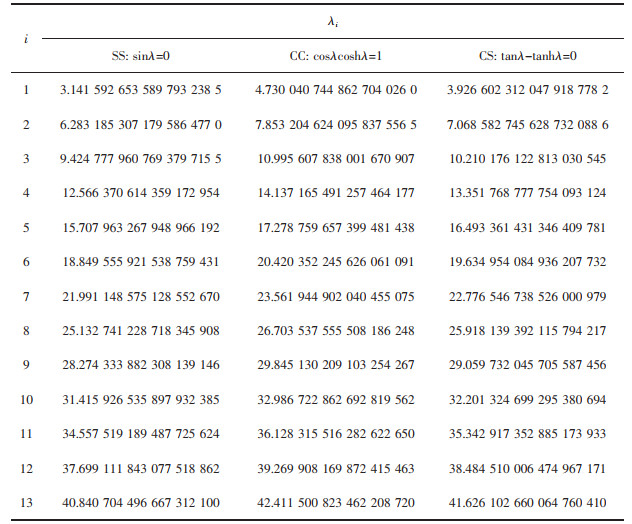
式(16)中:λi为第i阶经典梁本征值,可用经典梁本征方程求解,其中第1阶至第13阶经典梁本征值和本征方程分别列于表 1。
|
|
表 1 经典梁本征方程与第i阶本征值 |
将式(16)代入式(11a),ψx可确定。对于具有SS边界条件的梁:
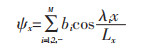
|
(17a) |
式(17a)中:
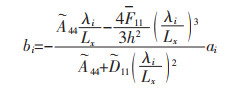
|
(17b) |
对于具有CC边界条件的梁:
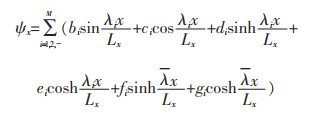
|
(18a) |
式(18a)中:

|
(18b) |
对于具有CS边界条件的梁:
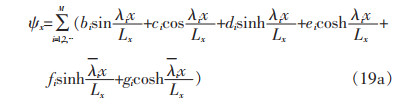
|
(19a) |
式(19a)中:

|
(19b) |
值得注意的是式(15)—式(19)可满足式中所有位移边界条件式(14)。通过将w和ψx代入下面的表达式,可以得到关于ai的三次代数方程:
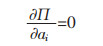
|
(20) |
式(20)中:П=U+V,应变能U为:
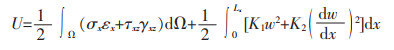
|
(21a) |
外力功V为:
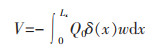
|
(21b) |
式(21b)中:Q0是集中荷载;δ(x)是Dirac函数。对于给定荷载(如横向集中荷载(Q0))和其他已知系数的梁,ai可采用Newton-Raphson迭代法或其他等效方法求解出来。然后,通过将这些系数回代入式(15)—式(19),可以完全确定w与ψx。为简洁起见,非线性代数方程组和求解过程略去。
值得进一步说明的是,本文所采用挠度试函数是经典梁本征函数,该级数在空间上是正交完备的,挠度试函数与转角方程具有特定的解析形式并且满足全部的边界条件,因而可以通过增加级数用Ritz方法逼近于精确解。用经典梁本征函数去求解高阶剪切变形梁的非线性问题,这是本文的特色创新之处。此外,针对多种复杂载荷或多种边界条件情形,多级数CBEF-Ritz方法也不失为是一种高效分析求解结构非线性问题的一般方法。从方法论层法上来说,该方法应用价值更广。
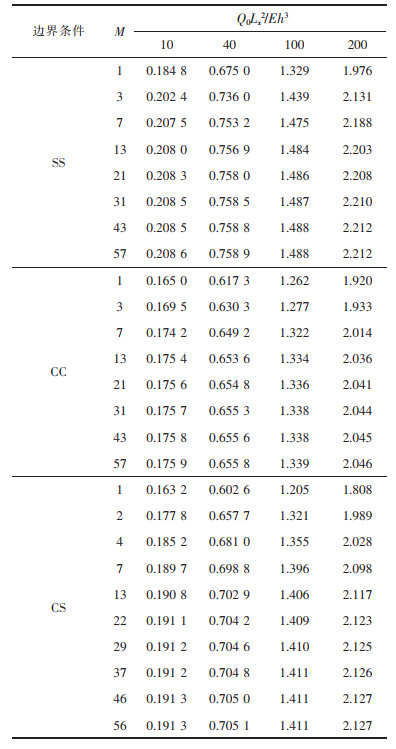
3 结果和讨论 3.1 收敛性研究首先对3种具有不同边界条件的铝梁在中心集中荷载(Q0)作用下的中心挠度进行了多级数CBEF-Ritz方法的收敛性研究,详见表 2。其中,铝梁的材料性能E=70 GPa,v=0.3,长厚比(Lx/h)=20。无量纲地基刚度(k1,k2)=(50, 5),其中,k1=K1Lx4/Eh3,k2=K2Lx2/Eh3。无量纲荷载和无量纲中心挠度分别定义为Q0Lx3/Eh4和wcenter/h。在此需要说明的是,由于在集中荷载作用下梁中心挠度结果的收敛性比较慢,为了避免冗繁,仅选择了部分级数的结果展示于表 2。
|
|
表 2 依据不同级数M双参数弹性地基上铝梁非线性弯曲的计算结果比较 |
从表 2可以看出,多级数CBEF-Ritz方法可以通过增加级数逼近精确解。兼顾计算的简洁性与精度,在以下计算中使用M=13。需要特别注意的是,在计算过程中,级数越大对经典梁本征值的精度要求越高。
3.2 同类文献数值结果比较为保证本方法的有效性和准确性,文中计算了Pasternak弹性地基上各向同性梁的中心挠度-荷载曲线,并与文献[11]采用边界积分方程法的结果进行了比较,如图 2所示。其中,r= 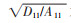
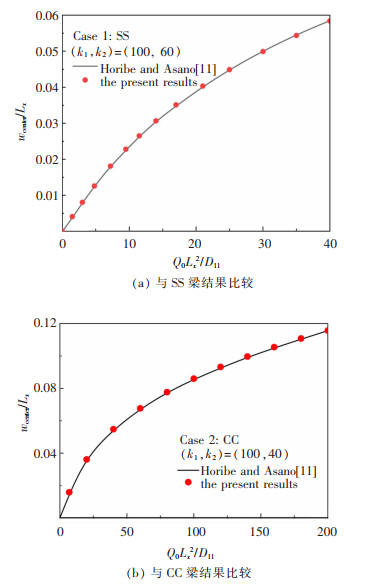 |
| 图 2 双参数弹性地基梁的几何与坐标非线性弯曲比较 |
对梁的弯曲响应进行了参数分析。无量纲地基刚度参数(k1,k2)=(50, 0)表示Winkler弹性地基,(k1,k2)=(50, 5)表示Pasternak弹性地基,(k1,k2)=(0, 0)表示无弹性地基梁。
弹性地基对中心集中荷载作用下梁的非线性弯曲的影响如图 3所示,当无量纲集中荷载不变时,Winkler弹性地基上的梁的最大挠度介于无地基梁和Pasternak弹性地基上的梁之间。主要原因在于,Winkler地基计及了地基反力与梁挠度之间的正比关系,而Pasternak地基又计及了地基与梁之间剪切力的影响。从图 3中也可以观察到边界条件对梁挠度的影响,在相同荷载与相同地基条件下,CS梁的挠度介于SS梁和CC梁之间。
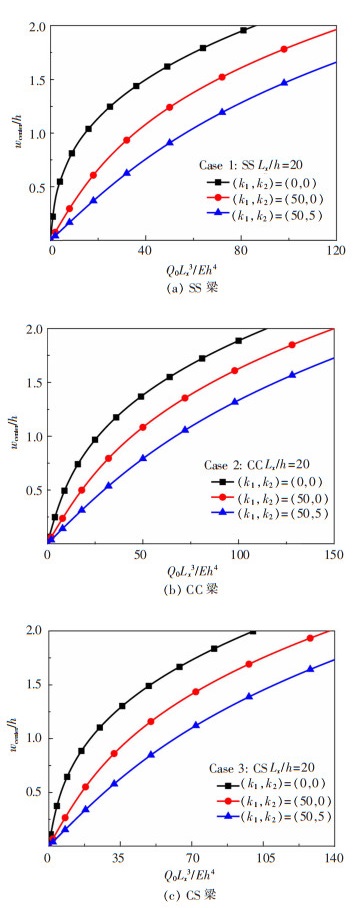 |
| 图 3 弹性地基对集中荷载作用下梁非线性弯曲的影响 |
长厚比对集中荷载(Q0)作用下梁的非线性弯曲的影响如图 4所示。结果表明,当无量纲集中荷载不变时,随着长厚比的减小,挠度会增大。若梁较厚时,高阶剪切效应对挠度的影响则不可忽略。
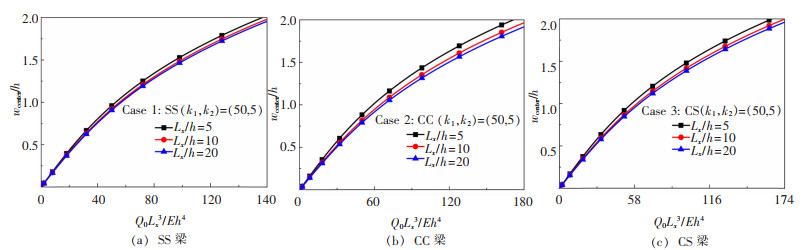 |
| 图 4 长厚比对中心集中荷载作用下Pasternak弹性地基梁非线性弯曲的影响 |
不同无量纲中心集中荷载(Q0)对Pasternak弹性地基梁的无量纲挠度和转角的影响如图 5和图 6所示。可以观察到,最大挠度和零转角出现在集中荷载位置或附近,而简支端部附近的转角接近于常数,其主要原因在于简支端部附近的弯矩近似为零。
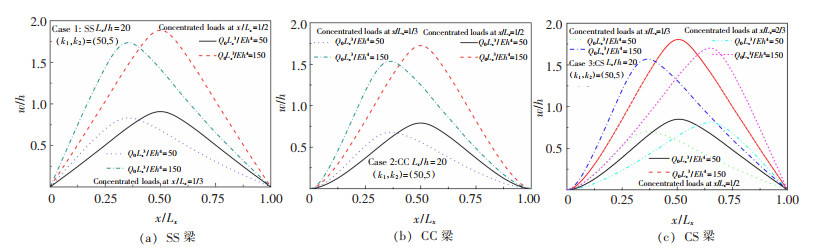 |
| 图 5 不同集中荷载对Pasternak弹性地基梁挠度的影响 |
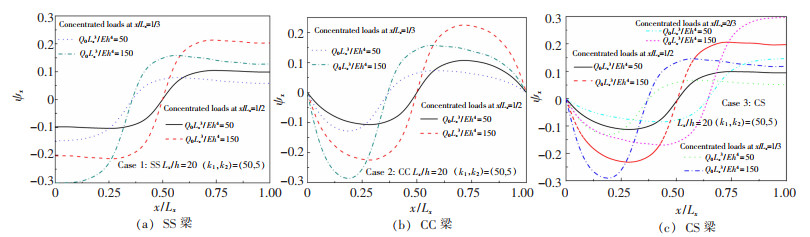 |
| 图 6 不同集中荷载对Pasternak弹性地基梁转角的影响 |
本文首次提出了用于高阶剪切变形梁非线性弯曲分析的多级数CBEF-Ritz方法,其中挠度试函数与转角方程完全满足位移边界条件。针对多种复杂载荷或多种边界条件情形,该方法也是一种高效分析求解结构非线性问题的一般方法。最后研究了集中荷载作用下双参数弹性地基上高阶剪切变形梁的非线性弯曲响应。重要结论如下:
1)通过增加级数,采用多级数CBEF-Ritz方法可以逼近高阶剪切变形梁的精确解。
2)在其他参数相同的情况下,位于Winkler弹性地基上的梁的最大挠度介于无地基梁和位于Pasternak弹性地基上的梁之间,且CS梁的最大挠度介于SS梁和CC梁之间。随着长厚比的减小,最大挠度增大。若梁较厚时,高阶剪切效应对挠度的影响则不可忽略。
3)在集中荷载作用下,最大挠度和零转角出现在集中荷载位置或附近,而简支端部附近的转角接近于常数。
| [1] |
VAZ M A, ARIZA A J. Quasi-static response of linear viscoelastic cantilever beams subject to a concentrated harmonic end load[J]. International Journal of Non-Linear Mechanics, 2013, 54: 43-54. DOI:10.1016/j.ijnonlinmec.2013.03.009 |
| [2] |
WANG C M, KITIPORNCHAI S. Shooting optimization technique for large deflection analysis of structural members[J]. Engineering Structures, 1992, 14(4): 231-240. DOI:10.1016/0141-0296(92)90011-E |
| [3] |
DADO M, AL-SADDER S. A new technique for large deflection analysis of non-prismatic cantilever beams[J]. Mechanics Research Communications, 2005, 32(6): 692-703. DOI:10.1016/j.mechrescom.2005.01.004 |
| [4] |
ANSARI R, SHOJAEI M F, GHOLAMI R. Size-dependent nonlinear mechanical behavior of third-order shear deformable functionally graded microbeams using the variational differential quadrature method[J]. Composite Structures, 2016, 136: 669-683. DOI:10.1016/j.compstruct.2015.10.043 |
| [5] |
CHEN L. An integral approach for large deflection cantilever beams[J]. International Journal of Non-Linear Mechanics, 2010, 45(3): 301-305. DOI:10.1016/j.ijnonlinmec.2009.12.004 |
| [6] |
BELENDEZ T, PÉREZ-POLO M, NEIPP C, et al. Numerical and experimental analysis of large deflections of cantilever beams under a combined load[J]. Physica Scripta, 2005, 118: 61-65. |
| [7] |
RAZZAQ Z, COSKUN H, LI X J, et al. LRFD approach for FRP-REinforced thermoplastic beams[J]. Journal of Reinforced Plastics and Composites, 2009, 28(22): 2749-2759. DOI:10.1177/0731684408093495 |
| [8] |
VITALIANI R V, GASPARINI, A M, SAETTA A V. Finite element solution of the stability problem for nonlinear undamped and damped systems under nonconservative loading[J]. International Journal of Solids and Structures, 1997, 34(19): 2497-2516. DOI:10.1016/S0020-7683(96)00115-1 |
| [9] |
KASIRAJAN P, AMIRTHAM R, REDDY J N. Surface and non-local effects for non-linear analysis of Timoshenko beams[J]. International Journal of Non-Linear Mechanics, 2015, 76: 100-111. DOI:10.1016/j.ijnonlinmec.2015.06.006 |
| [10] |
NGUYEN D K, NGUYEN K V, DINH V M, et al. Nonlinear bending of elastoplastic functionally graded ceramic-metal beams subjected to nonuniform distributed loads[J]. Applied Mathematics and Computation, 2018, 333: 443-459. DOI:10.1016/j.amc.2018.03.100 |
| [11] |
HORIBE T, ASANO N. Large deflection analysis of beams on two-parameter elastic foundation using the boundary integral equation method[J]. JSME International Journal Series A, 2001, 44(2): 231-236. DOI:10.1299/jsmea.44.231 |
| [12] |
SOLANO-CARRILLO E. Semi-exact solutions for large deflections of cantilever beams of non-linear elastic behaviour[J]. International Journal of Non-Linear Mechanics, 2009, 44(2): 253-256. DOI:10.1016/j.ijnonlinmec.2008.11.007 |
| [13] |
BORBONI A, DE SANTIS D. Large deflection of a non-linear, elastic, asymmetric Ludwick cantilever beam subjected to horizontal force, vertical force and bending torque at the free end[J]. Meccanica, 2014, 49(6): 1327-1336. |
| [14] |
SHVARTSMAN B S. Direct method for analysis of flexible cantilever beam subjected to two follower forces[J]. International Journal of Non-Linear Mechanics, 2009, 44(2): 249-252. DOI:10.1016/j.ijnonlinmec.2008.11.004 |
| [15] |
HUMER A. Elliptic integral solution of the extensible elastica with a variable length under a concentrated force[J]. Acta Mechanica, 2011, 222(3/4): 209-223. |
| [16] |
LI D K, LI X F. Large deflection and rotation of Timoshenko beams with frictional end supports under three-point bending[J]. Comptes Rendus Mécanique, 2016, 344(8): 556-568. DOI:10.1016/j.crme.2016.01.007 |
| [17] |
SU M N, YOUNG B. Design of aluminium alloy stocky hollow sections subjected to concentrated transverse loads[J]. Thin-Walled Structures, 2018, 124: 546-557. DOI:10.1016/j.tws.2017.12.015 |
| [18] |
WANG Y Q, CHANG T, SHI Y J, et al. Experimental study on the deformation behavior of symmetric stainless steel I-beams[J]. Applied Mechanics and Materials, 2011(94/95/96): 18-24. |
| [19] |
YANG K H, MUN J H, LEE J S. Flexural tests on pre-tensioned lightweight concrete beams[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2014, 167(4): 203-216. DOI:10.1680/stbu.12.00003 |
| [20] |
毛丽娟, 马连生. 剪切可变形梁非线性静态响应的精确解[J]. 应用力学学报, 2017, 34(1): 27-32. |
| [21] |
张旭, 侯祥林, 孙凤久. 简支梁大变形的优化算法[J]. 应用力学学报, 2006, 23(4): 668-672. DOI:10.3969/j.issn.1000-4939.2006.04.033 |
| [22] |
HEYLIGER P R, REDDY J N. A higher order beam finite element for bending and vibration problems[J]. Journal of Sound and Vibration, 1988, 126(2): 309-326. DOI:10.1016/0022-460X(88)90244-1 |
 2022, Vol. 42
2022, Vol. 42