| 基于不同优化目标的钢纤维混凝土力学性能试验 |
2. 江西省环境岩土与工程灾害控制重点实验室,江西 赣州 341000
2. Jiangxi Province Key Laboratory of Environmental Geotechnical Engineering and Hazards Control, Ganzhou 341000, Jiangxi, China
桥梁伸缩缝锚固区作为桥梁结构的过渡段,该位置处的混凝土在使用过程中往往会受到车辆冲击和疲劳荷载作用,受力情况较为复杂。与桥梁中的其他结构相比,桥梁伸缩缝锚固区的钢纤维混凝土需要在满足混凝土流动性要求的前提下,具有更高的抗变形性能及弯曲韧性,从而延长钢纤维混凝土的使用寿命。
对钢纤维混凝土的物理力学性能展开研究,有利于在实际工程应用中更好地发挥钢纤维的优异性能,提高其使用寿命。Khallo与Gao等研究发现钢纤维能够显著改善混凝土在韧性、抗剪强度、弹性模量和泊松比等方面的性能,且随着钢纤维长径比和掺量的增大,改善效果更佳,其中,纤维掺量的影响更显著,但钢纤维对混凝土抗压强度的影响并不显著[1-2]。Mirsayah等采用直剪试验研究了钢纤维混凝土在剪切方面的力学性能,研究得出了剪切强度和剪切韧性在加入钢纤维后提高较为明显[3]。吴浩等研究了不同钢纤维对混凝土流动性的影响,发现镀铜微丝钢纤维对流动性影响最显著,而铣削型纤维的影响最小[4]。在此基础上,李清信、李悦等发现钢纤维掺量的增加会导致混凝土坍落度降低,抗压与抗折强度、劈裂强度、弯曲韧性和抗冲击性均有不同程度提高,且长钢纤维的影响更加显著[5-6]。此外,李长永等发现混凝土坍落度的降低是由于钢纤维在拌和物中的“棚架”效应,且随着砂率的增大,钢纤维混凝土的坍落度、抗压强度和劈裂抗拉强度先增大后减小[7]。王成启等发现碳纤维对混凝土的劈拉强度、断裂能和断裂韧性的增强效果显著低于钢纤维,且钢纤维对混凝土的增强作用具有明显的尺寸效应,表现为微细钢纤维能有效提高混凝土断裂能,而较大直径钢纤维对增强混凝土断裂韧性的效果更好[8]。刘胜兵、姚鹏飞和朱海峰等发现钢纤维对混凝土性能的影响较为显著,能够增大混凝土抗压强度,并改善其脆性特征,聚丙烯粗纤维主要作用是改善混凝土的延性[9-11]。曹小霞、徐礼华等在此基础上,还提出了最优掺量[12-13]。张艳军发现钢纤维和聚乙烯醇纤维均会降低混凝土的早期抗压强度,聚乙烯醇纤维的影响更加明显,但混凝土早期抗折强度有明显增强,钢纤维主要抑制宏观裂缝的发展[14]。
钢纤维混凝土抗压、劈拉和抗折方面的研究已经较为成熟,而对于不同优化目标的钢纤维混凝土性能差异试验研究尚未见报道。在寻找最优方案的过程中,需要考虑诸多方面的约束条件,并在满足各条件下,使最终的工程设计方案能够达到更高的要求,如成本更低或性能更优等,这个过程就是最优化的过程。为使钢纤维混凝土在浇筑完成后达到平整、密实、均匀的效果,本文拟在满足坍落度与扩展度要求的情况下,找到能够使力学性能达到更优的钢纤维混凝土。分别以抗压强度最大和功效系数法为目标对钢纤维混凝土进行配合比优化,研究其性能差异,从而得到在满足施工要求下性能更优的钢纤维混凝土,为类似工程提供借鉴。
1 钢纤维混凝土影响因素正交试验 1.1 正交试验方案以赣州某快速路工程为背景,应用树状图对钢纤维混凝土性能的影响因素展开分析,确定主要影响因素,从而为其配合比优化提供理论基础。钢纤维混凝土性能的影响因素如图 1所示。
 |
| 图 1 钢纤维混凝土性能影响因素 |
由图 1可知,影响钢纤维混凝土力学性能的因素有11个,其中关系到配合比设计的有4个参数,分别为钢纤维长度、钢纤维掺量、砂率及粗骨料的裹浆厚度。
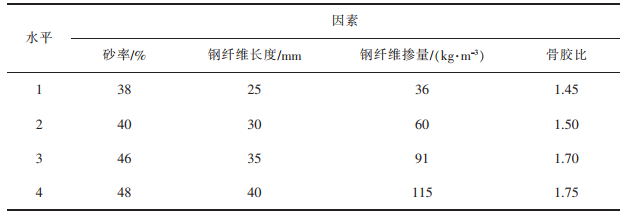
本文以钢纤维长度、钢纤维掺量、砂率及粗骨料的裹浆厚度作为正交试验因素,每个因素取4个水平,研究这4种因素对钢纤维混凝土性能的影响。因为条件所限,无法准确得到粗骨料裹浆厚度,但搅拌后得到的钢纤维混凝土拌合物中粗骨料能够均匀散布于混凝土拌合物中,故以粗骨料与胶凝材料的比值近似代替混凝土中粗骨料的裹浆厚度。各因素按实际工程中钢纤维混凝土配合比的取值范围取值,正交试验各因素取值如表 1所列。
|
|
表 1 正交试验各因素取值 |
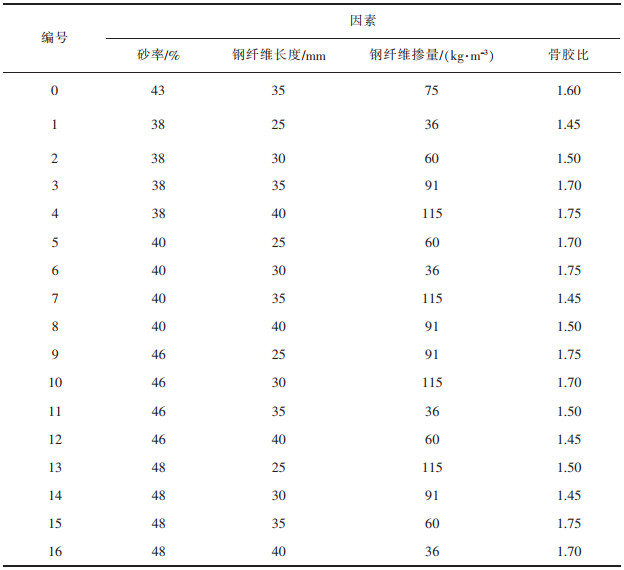
因为4个因素两两之间没有交互作用,故在进行正交试验设计时无需考虑各因素间交互作用的影响,本文严格按照正交试验表进行设计,如表 2所列。
|
|
表 2 正交试验设计 |
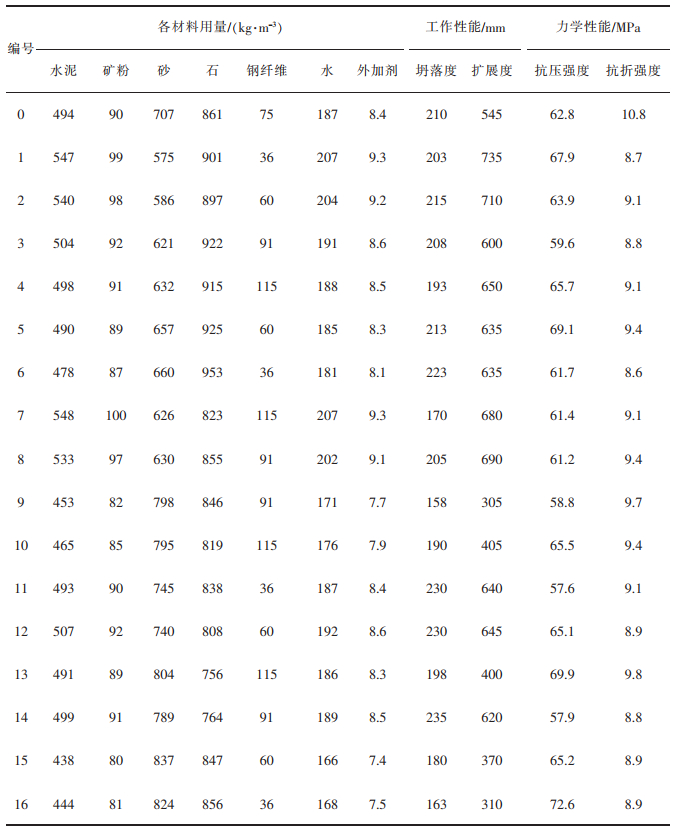
根据正交试验表中各影响因素的取值,得到试验中各组试块的配合比设计方案。参照规范《公路工程水泥及水泥混凝土试验规程》JTG E30-2005及《普通混凝土拌合物性能试验方法标准》GB/T 50080-2016中测量混凝土的坍落度和扩展度。参照《混凝土物理力学性能试验方法标准》GB/T 50081-2019的要求,制作棱柱体试块,每种试块3个,并使用电子万能试验机测量混凝土的抗压强度及抗折强度,试验过程如图 2-图 5所示,混凝土试块的最终破坏如图 6、图 7所示,试验结果如表 3所列。
 |
| 图 2 钢纤维混凝土工作性能试验装置 |
 |
| 图 3 钢纤维混凝土拌合物 |
 |
| 图 4 混凝土轴心抗压试验装置 |
 |
| 图 5 混凝土三点抗折试验装置 |
 |
| 图 6 轴心抗压下混凝土试件的破坏 |
 |
| 图 7 三点抗折下混凝土试件的破坏 |
|
|
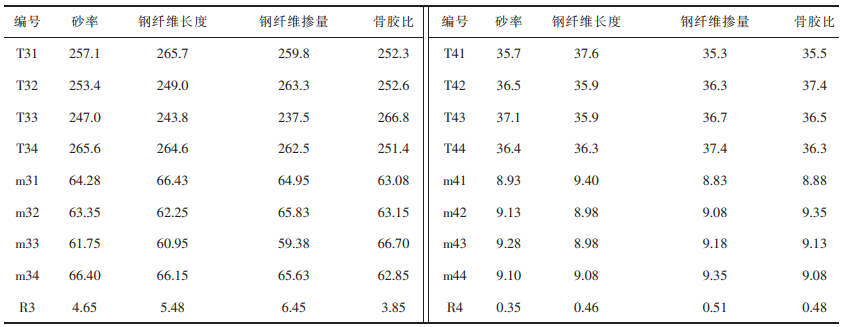
表 3 材料用量及试验结果 |
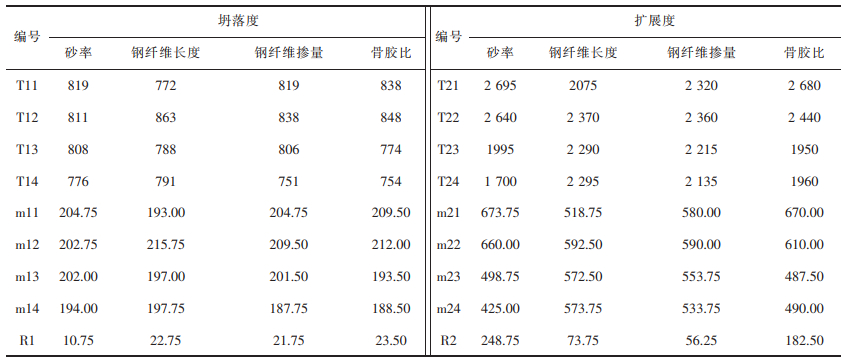
根据表 3所得到的钢纤维混凝土坍落度值、扩展度值与强度值的变化情况,对主要影响因素展开极差分析,得到钢纤维混凝土坍落度、扩展度与强度在4种参数影响下的变化情况,具体结果如表 4、表 5所列。
|
|
表 4 流动性变化情况 |
|
|
表 5 强度值变化情况 |
将表 4中的数值绘制成折线图,以研究不同因素对混凝土流动性能的影响情况,如图 8、图 9所示。
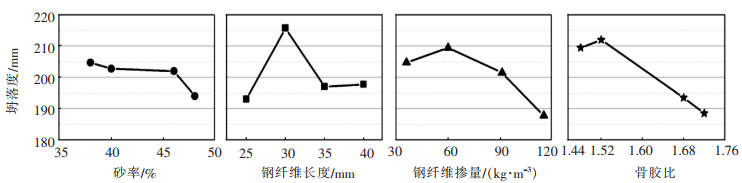 |
| 图 8 坍落度变化 |
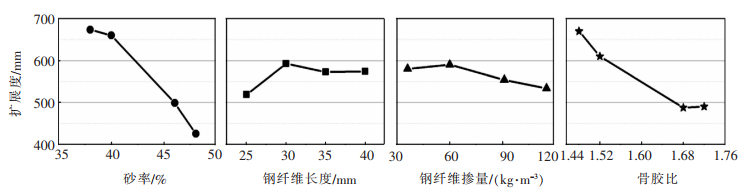 |
| 图 9 扩展度变化 |
从图 8、图 9及表 4可以看出,在钢纤维混凝土坍落度方面,砂率为38%时的坍落度为204.75 mm,随着砂率的增大,坍落度逐渐下降,在砂率为48%时达到最小值,为194.00 mm,较最大值下降了5.3%。坍落度随着钢纤维长度、钢纤维掺量及骨胶比的增大,表现出先增大后减小的变化趋势,并在钢纤维长度为30 mm、钢纤维掺量为60 kg/m3、骨胶比为1.50时达到最大值,最大值分别为215.75、209.50、212.00 mm。在钢纤维长度为25 mm、钢纤维掺量为115 kg/m3、骨胶比为1.75时达到最小值,最小值分别为193.00、187.70、188.5 mm,较最大值分别下降了10.5%、10.4%、11.1%。显然,骨胶比对于坍落度的影响最大,即骨胶比 > 钢纤维长度 > 钢纤维掺量 > 砂率。
在钢纤维混凝土扩展度方面,砂率为38%、骨胶比为1.45时扩展度达到最大值,分别为673.75 mm和670.00 mm。随着砂率与骨胶比的增大,扩展度呈下降趋势,在砂率为48%、骨胶比为1.75时,达到最小值,此时扩展度分别为425.00 mm和490.00 mm,与最大值相比分别下降了36.9%与27.2%。而随着钢纤维长度和掺量的增大,扩展度先增大后减小,并分别在钢纤维长度为35 mm、钢纤维掺量为60 kg/m3时达到最大值,分别为592.50 mm和592.00 mm,而在钢纤维长度为35 mm、钢纤维掺量为115 kg/m3时达到最小值,分别为572.50 mm和533.75 mm,与最大值相比分别下降了12.4%与9.5%。影响因素的显著性效果表现为:砂率 > 骨胶比 > 钢纤维长度 > 钢纤维掺量。通过对比还发现砂率对钢纤维混凝土扩展度的幅值比是砂率对坍落度幅值比的1.5倍,影响效果明显增大。
将表 5中的数值绘制折线图以研究不同因素对混凝土强度值的影响情况,如图 10、图 11所示。
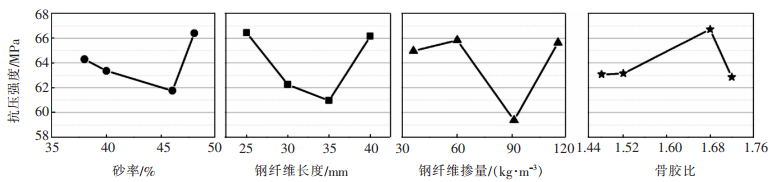 |
| 图 10 抗压强度变化 |
 |
| 图 11 抗折强度变化 |
在钢纤维混凝土抗压强度方面,随着砂率、钢纤维长度和钢纤维掺量的增大,抗压强度呈现先减小后增大的趋势,并分别在砂率为48%、钢纤维长度为25 mm、钢纤维掺量为60 kg/m3时达到最大值,抗压强度分别为66.4、66.425、65.825 MPa。在砂率为46%、钢纤维长度为35 mm、钢纤维掺量为91 kg/m3时达到最小值,分别为61.75、60.95、59.375 MPa,与最大值相比,分别下降了7.0%、8.2%、9.8%。而随着骨胶比的增大,抗压强度先增大后减小,在骨胶比为1.70时达到最大值,为66.7 MPa,在骨胶比为1.75时达到最小值,为62.85 MPa,与最大值相比下降了5.8%。显然,钢纤维的掺量和长度对抗压强度的影响明显大于砂率与骨胶比,即钢纤维掺量 > 钢纤维长度 > 砂率 > 骨胶比。
在钢纤维混凝土的抗折强度方面,随着砂率与骨胶比的增大,抗折强度呈现出先增大后减小的变化趋势,并在砂率为46%、骨胶比为1.50时达到最大值,分别为9.275 MPa和9.35 MPa。在砂率为38%、骨胶比为1.45时达到最小值,分别为8.925 MPa和8.875 MPa,与最大值相比分别下降了3.8%和5.1%。抗折强度随着钢纤维长度的增加呈现先减小后增大的变化规律,在钢纤维长度为25 mm时达到最大值,为9.400 MPa,在钢纤维长度为30 mm和35 mm时,抗折强度相对较少,为8.975 MPa,与最大值相比下降了4.8%。随着钢纤维掺量的增大,混凝土抗折强度呈递增趋势,在钢纤维掺量为115 kg/m3时达到最大值,为9.350 MPa,在钢纤维掺量为36 kg/m3时达到最小值,为8.825 MPa,与最大值相比下降了5.4%。
此外,通过对比发现,骨胶比对钢纤维混凝土抗折强度的影响相对混凝土的抗压强度有所增大,这主要是由于其他因素对钢纤维混凝土抗折强度影响的幅值比与其对钢纤维混凝土抗压强度影响的幅值比相比,均有一定程度的下降,相对变化幅度较小。
1.3 钢纤维混凝土配合比优化建议采用MATLAB进行多目标规划,运用功效系数法,使抗压与抗折强度乘积同时达到最优,对钢纤维混凝土力学性能以不同目标进行优化,并比较其性能差异,从而提出配合比优化建议。
功效系数法[15]是根据多目标规划原理,对每一项评价指标添加一个指定的系数,计算各指标实现满意值的程度,从而评估被研究对象的综合状况。本文中,记各参数下的钢纤维混凝土的抗压和抗折强度与其抗压和抗折强度最大值的比值为相应的功效系数,记抗压强度的功效系数为d1,抗折强度的功效系数为d2,总功效系数d=(d1×d2)1/2,因为抗压与抗折强度的最大值均为定值,当d值为最大时,亦为抗压与抗折强度乘积取最大值,从而得到此时混凝土的各参数的取值,算出优化后的配合比。本文拟根据上文的回归方程,运用MATLAB计算程序,在满足钢纤维混凝土坍落度与扩展度的情况下,分别以抗压强度达到最大和总功效系数达到最大为目标函数,得到两种不同的配合比设计方案,结果如表 6所列。
|
|
表 6 不同钢纤维混凝土配合比的主要参数取值 |
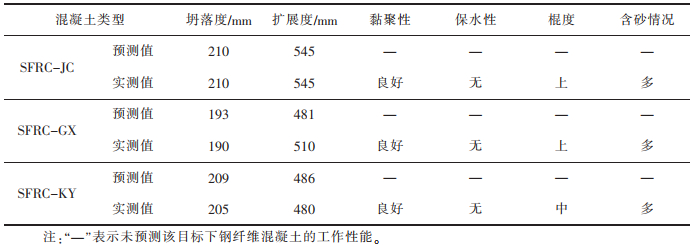
对以不同优化目标获得的钢纤维混凝土配合比展开工作性能的试验测试,并与回归方程所得的坍落度及扩展度预测值展开比较与分析,具体结果如表 7所列。从表 7可知,混凝土的坍落度和扩展度实测值与前述回归方程所得的预测值基本相同,坍落度误差小于5 mm,扩展度误差小于35 mm,均在试验允许范围内,且能够满足混凝土配合比设计要求。此外,3种钢纤维混凝土均具有良好的黏聚性、保水性及含砂情况,但SFRC-KY的棍度略差于SFRC-JC和SFRC-GX,这主要是由于SFRC-KY的浆体相对较少,插捣时存在石子阻塞,使流动性变差。
|
|
表 7 钢纤维混凝土工作性能评价 |
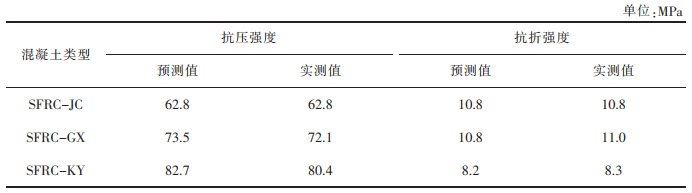
对以不同优化目标获得的钢纤维混凝土配合比展开力学性能的试验研究,并与回归方程所得的抗压及抗折强度预测值展开比较、分析,具体结果如表 8所列。从表 8可知,混凝土的抗压及抗折强度实测值与前述回归方程所得预测值基本相同,误差均小于3%,在试验允许范围内,且能够满足混凝土配合比设计要求。
|
|
表 8 不同钢纤维混凝土力学性能比较 |
比较3种不同配合比下钢纤维混凝土轴心抗压应力-应变曲线及三点抗折荷载-挠度曲线,如图 12和图 13所示。可以看出,3种不同配合比下的钢纤维混凝土具有明显的性能差异。在抗压性能方面,SFRC-GX与SFRC-KY与SFRC-JC峰值应力所对应的应变基本相同,但抗压强度均有所提高。其中SFRC-GX提高了14.8%,且在试块达到峰值应力后应力下降速度较SFRC-JC缓慢,混凝土塑性破坏特征进一步缓解,而SFRC-KY抗压强度虽提高了28%,但其应力在峰值后下降速度更快,塑性破坏更加明显。
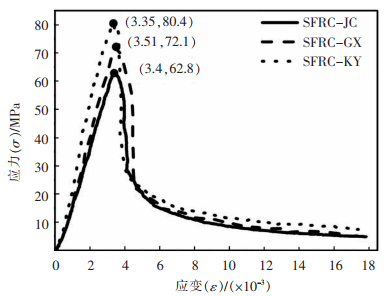 |
| 图 12 轴心抗压应力-应变曲线 |
 |
| 图 13 三点抗折荷载-挠度曲线 |
在抗折性能方面,SFRC-GX、SFRC-KY与SFRC-JC峰值荷载所对应的跨中挠度无显著变化。SFRC-GX的峰值荷载略高于SFRC-JC的峰值应力,且在峰值后的荷载下降趋势与速度明显优于SFRC-JC,但SFRC-KY的峰值荷载较SFRC-JC下降了22.6%,且在峰值荷载后其荷载下降速度较快,韧性性能较差,这是因为SFRC-KY的浆体相对较少,内部存在更多的孔隙,且钢纤维与浆体材料黏结效果较差而导致。
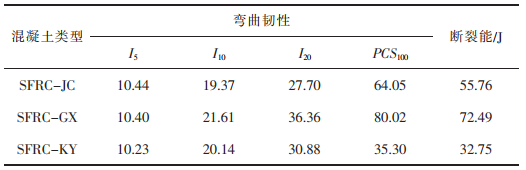
为了更进一步了解不同优化目标下钢纤维混凝土的性能差异,对SFRC-GX、SFRC-KY与SFRC-JC的弯曲韧性和断裂能展开研究,结果如表 9所列。
|
|
表 9 钢纤维混凝土的荷载-挠度曲线变化情况分析 |
弯曲韧性指标采用混凝土试件受弯初裂时挠度(δcr)的3.0倍、5.5倍、10.5倍所对应的荷载-挠度曲线面积与初裂时挠度(δcr)所对应的荷载-挠度曲线面积的比值(I5、I10、I20),从而判断混凝土的弯曲韧性情况。同时,根据文献[16]中的newkumar法判断混凝土的弯曲韧性,其具体方法为将混凝土的荷载-挠度曲线分为峰前(Tpre)和峰后(Tpwt, m),以特定的挠度(L/m)为变量,计算混凝土在加载过程中所消耗的能量,其韧性指标用PCSm表示,具体计算公式为:
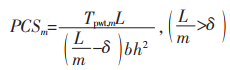
|
其中,Tpwt, m为峰后荷载-挠度曲线包围的面积,N·mm;L为梁的跨度,本文为300 mm;δ为应力峰值所对应的挠度,mm;b、h为构件的宽度和高度,均为100 mm;m为50的整倍数,取100。
断裂能[17]是指混凝土在荷载作用下形成单位面积裂缝所消耗的能量。混凝土中的微小裂缝在受到荷载作用时会发生裂纹扩展,而混凝土的断裂能越高,裂缝扩展的阻力越大,混凝土的韧性越好。通过选取相同的钢纤维混凝土与普通混凝土试块的扩展裂缝长度,计算各自的断裂能。
3种不同钢纤维混凝土的弯曲韧性如表 9所列,可以看出,SFRC-GX的I5与SFRC-JC基本相同,但I10、I20、PCS100分别提高了12%、31%、25%,而SFRC-KY的I5、PCS100较SFRC-JC分别下降了2%、45%,I10、I20也仅上升了4%和11%。此外,与SFRC-JC相比,SFRC-GX的断裂能提高了约30%,SFRC-KY断裂能下降了约41%。SFRC-GX表现出更加优异的弯曲韧性。
3 结论通过不同目标对钢纤维混凝土和普通混凝土制备,并对比有不同目标钢纤维混凝土的性能差异,主要结论有:
1)混凝土的坍落度、扩展度及抗压强度、抗折强度随各因素的变化呈不同的变化趋势,但均存在最优参数,混凝土的骨胶比及砂率对混凝土坍落度及扩展度影响更加显著,而钢纤维的参数对混凝土抗压及抗折强度的影响更加显著。
2)以功效系数法为优化目标得到的钢纤维混凝土抗压强度提高了14.8%,比例极限提高13.3%,延性系数提高3.4%,混凝土塑性破坏特征进一步得到缓解,且抗折强度略有提高,断裂能提高了30%,抗变形性能及弯曲韧性明显增大。而以抗压强度最大为优化目标得到的钢纤维混凝土抗压强度提高了28%,比例极限提高了33.4%,但其延性系数下降5.2%,混凝土塑性破坏有所加剧,且抗折强度下降了2.6%,断裂能下降41%,混凝土抗变形性能及弯曲韧性明显不足。
3)通过对以抗压强度最大与功效系数法为优化目标得到的钢纤维混凝土性能进行比较,发现以功效系数法优化得到的钢纤维混凝土的综合性能明显优于以抗压强度最大得到的钢纤维混凝土,在提高了其抗压强度的同时,也提高了抗折强度和弯曲韧性,满足了多方面性能要求。因此,在进行钢纤维混凝土配合比设计时,根据混凝土土材料在实际工程中的受力情况,宜采用考虑了多方面性能需求的功效系数法。
| [1] |
KHALOO A R, KIM N. Influence of concrete and fiber characteristics on behavior of steel fiber reinforced concrete under direct shear[J]. ACI Materials Journal, 1997, 94(6): 592-601. |
| [2] |
GAO J M, SUN W, MORINO K. Mechanical properties of steel fiber-reinforced, high-strength, lightweight concrete[J]. Cement and Concrete Composites, 1997, 19(4): 307-313. DOI:10.1016/S0958-9465(97)00023-1 |
| [3] |
MIRSAYAH A A, BANTHIA N. Shear strength of steel fiber-reinforced concrete[J]. ACI Materials Journal, 2002, 99(5): 473-479. |
| [4] |
吴浩, 王振地, 王玲, 等. 钢纤维类型和掺量对高强混凝土流动性的影响[J]. 低温建筑技术, 2017, 39(9): 1-3. |
| [5] |
李清信, 高存官, 孙庆文. 钢纤维掺量对混凝土性能的影响[J]. 江苏建材, 2015(2): 36-38. DOI:10.3969/j.issn.1004-5538.2015.02.012 |
| [6] |
李悦, 王兴雷, 丁庆军. 钢纤维长度与掺量对混凝土力学性能的影响[J]. 混凝土, 2017(7): 62-65. |
| [7] |
李长永, 赵顺波, 钱晓军. 砂率对剪切型钢纤维增强混凝土性能的影响[J]. 建筑材料学报, 2007, 10(2): 247-252. DOI:10.3969/j.issn.1007-9629.2007.02.022 |
| [8] |
王成启, 吴科如. 钢纤维和碳纤维混凝土力学性能的研究[J]. 建筑材料学报, 2003, 6(3): 253-256. DOI:10.3969/j.issn.1007-9629.2003.03.007 |
| [9] |
刘胜兵, 李维, 吴明丽, 等. 钢-聚丙烯混杂纤维轻骨料混凝土劈裂抗拉强度研究[J]. 价值工程, 2016, 35(32): 116-118. |
| [10] |
姚鹏飞. 钢-聚丙烯混杂纤维轻骨料混凝土抗压与抗折性能试验研究[D]. 武汉: 武汉工程大学, 2017.
|
| [11] |
朱海峰, 黄建平, 郑坤炎. 钢-PP混杂纤维混凝土坍落度及基本力学强度试验研究[J]. 贵州大学学报(自然科学版), 2019, 36(2): 90-95. |
| [12] |
曹小霞, 郑居焕. 钢纤维和聚丙烯粗纤维对活性粉末混凝土强度和延性的影响[J]. 安徽建筑工业学院学报(自然科学版), 2011, 19(2): 58-61. |
| [13] |
徐礼华, 夏冬桃, 夏广政, 等. 钢纤维和聚丙烯纤维对高强混凝土强度的影响[J]. 武汉理工大学学报, 2007(4): 58-60. |
| [14] |
张艳军. 桥梁伸缩装置锚固区混杂纤维混凝土力学性能试验研究[D]. 武汉: 武汉工程大学, 2018.
|
| [15] |
吴博, 赵法锁, 吴韶艳. 基于组合赋权-功效系数法的黄土边坡稳定性评价[J]. 灾害学, 2020, 35(2): 34-38. |
| [16] |
方圣恩, 张培辉, 洪华山. 纤维混凝土梁受弯试验及开裂弯矩计算公式[J]. 建筑材料学报, 2019, 22(4): 567-574. |
| [17] |
杨枫林, 赵亚松, 高建明. 再生混凝土断裂性能试验研究[J]. 江苏建材, 2019(2): 24-28. |
 2022, Vol. 42
2022, Vol. 42