| 基于响应面法的AUV阻力结构优化设计 |
自主式水下机器人(Autonomous Underwater Vehicles, AUV)以其潜深大、活动范围广、环境适应性强等特点,广泛应用于水下探测、水文监测、海洋学研究等方面[1-2]。AUV的形状不仅影响着总体的布局,其受到的阻力更是影响AUV的续航时间,故降低AUV航行受到的阻力具有重要意义。
早期的研究中,人们通过经验公式估算AUV的阻力,并结合算法对AUV进行减阻优化,以得到较优阻力特性的外形[3-4]。虽然采用经验公式能够快速得到AUV阻力值,但是经验公式仅适合用于湍流特征不明显且具有简单外形结构的AUV。近年来随着计算机技术的发展,计算流体力学方法(CFD)能够准确计算各类型AUV阻力值,不少学者利用算法和CFD仿真技术对AUV进行了减阻优化的研究[5-8]。然而CFD方法计算时间较长,特别是结合一些复杂的优化算法时,其优化计算时间随着迭代次数的增加而增加,占用大量计算机资源,计算效率低。响应面法是近年来颇受欢迎的一种优化方法,是一种利用构建的数学近似模型代替原本复杂的模型进行近似优化分析的一种方法,具有计算效率高,易于迭代等优点[9-10]。因此,本文采用CFD结合响应面方法对AUV阻力结构进行优化,用来减小AUV水下航行过程中所受到的阻力,提高续航时间。
本文以Myring型回转体为研究对象,利用拉丁超立方采样试验设计确定样本点,使用Fluent计算样本点对应的响应值。同时,结合二阶多项式构建近似模型,并采用MOGA多目标遗传算法对该回转体进行多目标优化。在保持原有体积前提下,降低航行阻力提高AUV续航能力,并通过试验验证优化的有效性。
1 参数化建模及仿真分析 1.1 Myring线型参数化建模AUV因自带能源进行水下作业,考虑到能源的限制和总体布置要求,选择阻力性能较好的带有平行中段的Myring型回转体,其线型如图 1所示。
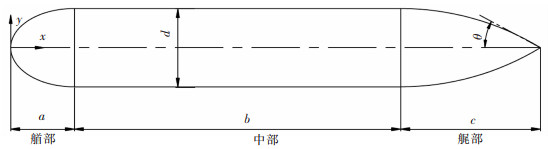 |
| 图 1 Myring线型 |
由图 1可知,流线型回转体组成包括三部分:艏部、中部和艉部,进流段和去流段均为平滑曲线,三部分线型表达式[3]为:
艏部:
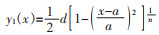
|
(1) |
中部:
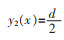
|
(2) |
艉部:
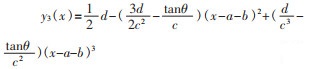
|
(3) |
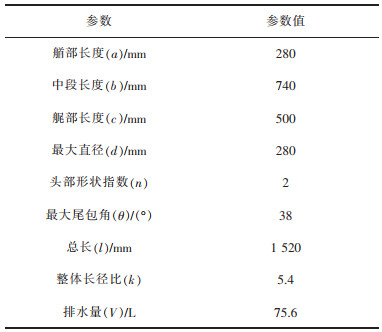
其中,yi(x)为各点处半径(i=1, 2, 3);x为轴向位置;a为艏部长度,mm;b为中段长度,mm;c为艉部长度,mm;d为最大剖面直径,mm;n为头部形状指数;θ为最大尾包角。通过改变6个参数a、b、c、d、n、θ可生成各种形状,本文优化的AUV质量不超过80 kg,根据所需排水体积计算公式,同时结合已有研究,当艏段长径比为0.75~2,艉段长径比为1~2.25[11],整体长径比(k)取5~8[12],头部形状指数(n)取1~4,尾包角(θ)取10°~40°[13]时,AUV具有良好的阻力性能,综上所述,Myring型回转体具体参数如表 1所列。在确定了参数后,利用SolidWorks进行参数化建模。
|
|
表 1 AUV模型参数 |
利用Fluent软件对模型进行流体仿真计算时,首先对导入的参数化模型建立流体域,然后将处理好的模型导入到ICEM中进行网格划分。由于模型头部尾部存在一定的曲率变化问题,需要对其进行局部网格加密,考虑到优化过程中模型随着参数变化而不断改变,故采用网格适应性更好的四面体非结构化网格划分方式。为了确保计算结果的精确性,流体域采用圆柱形,速度入口距离模型头部2倍的模型长度,压力出口距离模型尾部3倍的模型长度,壁面距模型中心线1.5倍模型长度[14]。模型网格加密划分如图 2所示。
 |
| 图 2 网格加密 |
网格划分完毕后,选取SST k-ω湍流模型[15]和SIMPLE压力-速度耦合计算方法,采用PRESTO离散格式压力方程以及Second Order Upwind格式动量方程,并设置所有参数的收敛残差为10-3,迭代次数700步,计算了来流速度1.5 m/s时模型阻力。
2 AUV阻力结构优化 2.1 试验设计在构造响应面模型时,需选择合适的试验设计方法,以较少的样本点获取精确的设计变量与响应值的关系。由于拉丁超立方采样,能够将设计变量均匀不重复的分成n等分,能够保证每一个设计变量范围的全覆盖,从而得到设计空间内各个设计变量对响应值的影响情况[16],因此本文选择该方法进行实验设计样本点的生成。本文分别以艏段长度(a)、艉段长度(c)、头部形状指数(n)及尾包角(θ)为研究对象,设计变量的取值范围如表 2所列。
|
|
表 2 设计变量取值范围 |
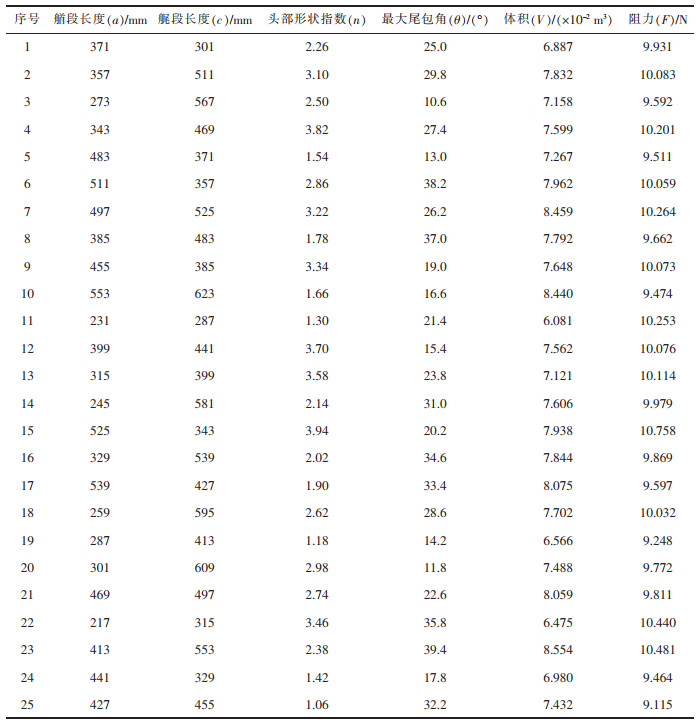
根据拉丁超立方采样试验设计方法确定样本点数量为25,即每个设计变量在取值范围空间内均匀不重复的分成25等分,进行仿真计算,计算过程中取恒定速度1.5 m/s,得到的25个样本点数据结果如表 3所列。
|
|
表 3 拉丁超立方采样试验设计 |
构造响应面时,通常选择二阶多项式构建近似模型[17],其数学表达式为:
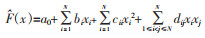
|
(4) |
式(4)中: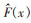
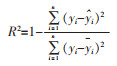
|
(5) |
式(5)中:n为试验样本点的数量;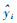
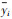
对样本点数据进行拟合,拟合结果如图 3所示,可以看出,标准二阶响应面模型的预测值和Fluent仿真值的拟合度较高。说明了建立的近似模型有效,样本点数据精确有效,故可以用作后续的多目标优化。
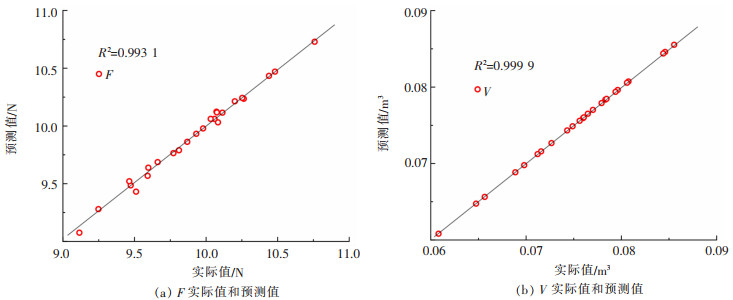 |
| 图 3 模型实际值与预测值对比 |
灵敏度用来反映设计变量与输出结果之间的关系和影响程度[18],通过灵敏度分析,确定本次设计变量对阻力的影响程度,可为同类型AUV阻力结构设计提供一定参考依据,同时,找到并忽略影响程度较小的设计变量,可减少优化时间。图 4为此次4个设计变量与AUV阻力值的灵敏度关系,由图 4可知,4个设计变量对阻力的影响程度都比较大,其中头部形状指数(n)对阻力影响最大,艏段长度(a)影响最小,其次是尾包角(θ)及艉段长度(c)。
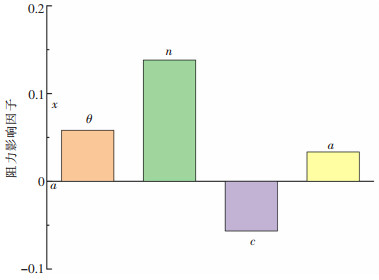 |
| 图 4 设计变量与阻力的灵敏度关系 |
AUV阻力结构设计时,希望受到的阻力越小越好,同时考虑到总体布置要求,因此,进行AUV阻力结构优化时,是阻力与体积的多目标优化问题。本次对该回转体进行多目标优化,以阻力和体积最小为目标函数,建立如式(6)所示的多目标优化数学模型:
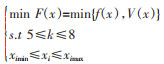
|
(6) |
式(6)中:x={a, c, n, θ}T为设计变量;目标函数f(x)表示AUV外形阻力;目标函数V(x)为外形体积(不小于7.564×10-2 m3);k为约束条件;ximin和ximax分别为设计变量的上下限。
本文选取100组初始样本数,每次迭代的样本数为100,最大迭代数量为20,保留3个候选点,利用MOGA遗传算法[19]进行计算,得到如图 5所示的Pareto优化解集。
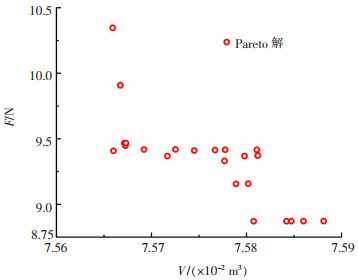 |
| 图 5 Pareto优化解集 |
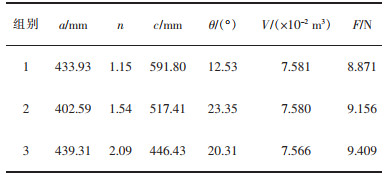
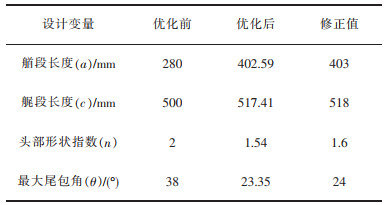
从图 5中选取了3组较优解如表 4所列,其中组别1阻力最小,组别2介于组别1和组别3之间。由于组别1的设计参数导致首尾过于尖锐,不利于加工更不利于相关仪器的安装,因此,本次选择组别2作为最终的优化设计方案。为了便于实际加工和仪器安装,对优化后的数据进行修正处理,结果如表 5所列。
|
|
表 4 优化设计候选点 |
|
|
表 5 优化前后的设计变量及修正值 |
在完成AUV外形多目标优化后,需对优化结果有效性进行验证,通过对比优化前后的结果分析判断。利用表 5优化后的参数修正值,建立有限元模型并导入到Fluent进行阻力分析,其结果如表 6所列。
|
|
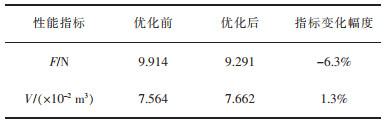
表 6 AUV外形优化前后性能指标 |
由表 6可知,经过多目标优化后AUV外形阻力及体积,相比之前阻力降低了6.3%,体积增大了1.3%,在满足设备安装的空间要求下,达到了减小阻力的效果,有效地提高了AUV的综合性能。
3 试验验证为了进一步验证优化结果的有效性,加工了样机并在循环水槽中进行测试。采用单杆连接固定模型,固定点设置在模型重心处,将水密的六分力天平置于回转体轴线处且固定在支杆上。当六分力天平受到外力作用下,输出电信号到另一端连接的应变放大器中经过一系列转换,最终输出试验结果。试验中模型置于水中固定不动,且模型处于水平直航状态,改变水的流速,读取六分力天平传感器数值即可获取不同速度下模型的阻力,测试如图 6所示。
 |
| 图 6 试验测试 |
本次分别以速度v=0.3、0.6、0.9、1.2、1.5 m/s进行试验,每完成一次试验后需等待水流静止后再进行下一次试验,以减小误差。为了与仿真结果分析比较,在Fluent中对模型施加相同的输入速度,计算对应的输出阻力值,两者结果如图 7所示,由图 7可知,两者的结果比较接近,验证了本次优化结果的合理性。
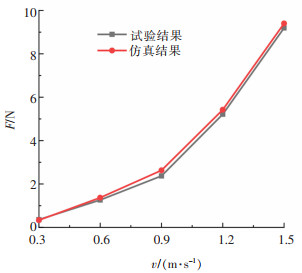 |
| 图 7 仿真与试验结果对比 |
1)本文以Myring型AUV外形结构为研究对象,利用SolidWorks进行了参数化三维建模,然后利用Fluent软件,进行了直航阻力仿真分析,得到了AUV航行时的阻力值。
2)确定了设计变量的取值范围,利用拉丁超立方采样试验设计方法确定了样本点,采用Fluent计算样本点对应的响应值。利用二阶多项式构建了近似模型,并进行了模型拟合精度判断及灵敏度分析。
3)建立了以整体长径比为约束条件,以阻力和体积最小的多目标函数,并采用MOGA多目标遗传算法求解,优化后结果表明,AUV阻力减小了6.3%,体积增大了1.3%,提高了AUV的总体性能。
| [1] |
黄琰, 李岩, 俞建成, 等. AUV智能化现状与发展趋势[J]. 机器人, 2020, 42(2): 215-231. |
| [2] |
曹少华, 张春晓, 王广洲, 等. 智能水下机器人的发展现状及在军事上的应用[J]. 船舶工程, 2019, 41(2): 79-84. |
| [3] |
MYRING D F. A theoretical study of body drag in subcritical axisymmetric flow[J]. Aeronautical Quarterly, 1976, 27(3): 186-194. DOI:10.1017/S000192590000768X |
| [4] |
LUTZ T, WAGNER S. Drag reduction and shape optimization of airship bodies[J]. Journal of Aircraft, 1998, 35(3): 345-351. DOI:10.2514/2.2313 |
| [5] |
IGNACIO L C, VICTOR R R, FRANCISCO D R R, et al. Optimized design of an autonomous underwater vehicle, for exploration in the Caribbean Sea[J]. Ocean Engineering, 2020, 187: 106184. |
| [6] |
SAGHAFI M, LAVIMI R. Optimal design of nose and tail of an autonomous underwater vehicle hull to reduce drag force using numerical simulation[J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2019, 234(1): 76-88. |
| [7] |
CHEN X, WANG P, ZHANG D Y, et al. Gradient-based multidisciplinary design optimization of an autonomous underwater vehicle[J]. Applied Ocean Research, 2018, 80: 101-111. DOI:10.1016/j.apor.2018.08.006 |
| [8] |
李靖璐, 王鹏, 陈旭, 等. 基于FFD的翼身融合水下滑翔机外形优化设计[J]. 西北工业大学学报, 2020, 38(3): 459-464. DOI:10.3969/j.issn.1000-2758.2020.03.001 |
| [9] |
张勇, 周忠贺, 蒋明虎, 等. 基于响应面法的旋风分离器结构参数的优化[J]. 流体机械, 2018, 46(12): 32-38. DOI:10.3969/j.issn.1005-0329.2018.12.006 |
| [10] |
胡俊峰, 杨展宏, 徐贵阳. 基于响应面法的微操作平台可靠性稳健设计[J]. 振动与冲击, 2017, 36(15): 245-252. |
| [11] |
WON D J, KIM J, KIM J. Design optimization of duct-type AUVs using CFD analysis[J]. Intelligent Service Robotics, 2015, 8(4): 233-245. DOI:10.1007/s11370-015-0179-9 |
| [12] |
STEVENSON P, FURLONG M, DORMER D. AUV design-shape, drag and practical issues[J]. Sea Technology, 2009, 50(1): 41-44. |
| [13] |
王妹婷, 齐永锋, 汤方平, 等. 水下机器人外形优化设计[J]. 机床与液压, 2014, 42(5): 76-79. DOI:10.3969/j.issn.1001-3881.2014.05.022 |
| [14] |
STRYCZNIEWICZ K, DREŻEK P. CFD approach to modelling hydrodynamic characteristics of underwater glider[J]. Transactions on Aerospace Research, 2019, 2019(4): 32-45. DOI:10.2478/tar-2019-0021 |
| [15] |
高婷, 庞永杰, 王亚兴, 等. 水下航行器水动力系数计算方法[J]. 哈尔滨工程大学学报, 2019, 40(1): 174-180. |
| [16] |
SHIELDS M D, ZHANG J X. The generalization of Latin hypercube sampling[J]. Reliability Engineering & System Safety, 2016, 148: 96-108. |
| [17] |
周红明, 余松青, 周闻青, 等. 基于二阶多项式模型的焊缝缺陷几何量定征技术[J]. 机械设计与制造, 2016(6): 222-225. DOI:10.3969/j.issn.1001-3997.2016.06.059 |
| [18] |
唐军, 杨书麟, 秦智. 水下机器人耐压舱结构设计及参数优化[J]. 江西理工大学学报, 2020, 41(5): 88-95. |
| [19] |
ILLAHI F, EL-AMIN I, MUKHTIAR M U. The application of multiobjective optimization technique to the estimation of electric arc furnace parameters[J]. IEEE Transactions on Power Delivery, 2018, 33(4): 1727-1734. DOI:10.1109/TPWRD.2017.2758320 |
 2021, Vol. 41
2021, Vol. 41