| 齿轮钢20CrMnTi方坯凝固过程传热数值模拟 |
1b. 北京科技大学材料科学与工程学院,北京 100083;
2. 江苏沙钢集团淮钢特钢有限公司,江苏 淮安 223001
1b. School of materials science and engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Jiangsu Shagang Group Huai Steel Special Steel Corporation, Huaian 223001, Jiangsu, China
近年来,我国引进和新开发的齿轮钢种有碳素结构钢、Cr-Mo钢、Cr-Mn钢、Cr-Mn-B钢、Cr-Ni-Mo钢和Cr钢,但目前市场的主流齿轮钢种仍是20CrMnTi,因其成本低、工艺生产成熟, 已经渗透到了工业制造中,在齿轮钢市场仍占有较大的份额[1-2]。但随着齿轮钢需求量的急剧增加和质量要求的不断提高,通过提高铸坯的质量来改善齿轮钢的性能已成关键所在。
铸坯凝固过程的本质为传热,其过热的钢水先后经过结晶器、二冷区及空冷区冷却。在此过程中热量以热传导、热对流、热辐射的形式向外界传输热量,直至铸坯完全凝固。铸坯的质量与温度场的分布紧密相连,因此研究连铸工艺参数对其温度场的影响,对提高铸坯的质量具有重要意义。在此方面,许多研究者做了相关的工作。张振学[3]等通过对大方坯凝固传热的数值模拟,研究了拉速对铸坯横截面各特征点温度和坯壳厚度的的影响;铁占鹏[4]等对20CrMnTi大方坯凝固过程进行数值模拟得出:拉速和过热度的增加将引起铸坯表面温度升高及坯壳厚度减少。李璐[5]等通过对小方坯凝固传热模拟研究,得出小方坯在凝固过程中温度及坯壳厚度的变化趋势,并提出了解决角部温降的措施。本文以国内某钢厂生产的20CrMnTi齿轮钢为例,用ProCAST软件建立了200 mm×200 mm方坯凝固传热模型,研究了不同连铸工艺参数(过热度、拉速、二冷水量)对凝固过程温度场的影响。
1 数学模型的建立 1.1 模型的基本假设由于铸坯在凝固过程中传热的复杂性,不仅有温度的变化还有钢液在凝固过程的相变等其它因素。为了科学合理的建立模型,特对模型假设如下[6-10]:
(1) 钢液在弯月面处的复杂传热不做特殊处理,弯月面的钢液温度即为浇注温度(液相线温度+过热度)。
(2) 钢的热物性参数不随空间位置的改变而变化,只考虑温度对其影响。
(3) 由于铸坯在拉坯方向(Z方向,见图 1)上的导热量很小,只占总导热量的3%-6%, 故视为绝热,只考虑X、Y方向的传热,因此对铸坯进行二维空间传热处理。
 |
| 图 1 薄片模拟网格划分 |
(4) 不考虑结晶器振动对铸坯传热的影响。
(5) 各个不同区域的冷却水均匀地分布在铸坯的表面。
(6) 铸坯的内外弧传热条件相对称。
(7) 忽略铸坯因凝固收缩而引起的尺寸改变。
(8) 铸坯视为不可压缩材料,因粘滞性而引起的能耗不予以考虑。
1.2 凝固传热控制方程基于以上假设,方坯凝固传热过程中的二维非稳态传热微分控制方程可简化为[11]:
| $ \rho {{c}_{\text{p}}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left( \lambda \frac{\partial T}{\partial x} \right)+\frac{\partial }{\partial x}\left( \lambda \frac{\partial T}{\partial y} \right)\text{+}{{q}_{\text{v}}} $ | (1) |
式(1)中:ρ为钢液密度,kg /m3;cp为热容,J / kg·℃;λ为导热系数,w/m·℃;qv为内热源,J /(m3·s);T为温度,℃;t为时间,s。
1.3 初始条件在铸坯传热模型中,将结晶器弯月面附近钢液的温度作为初始条件(t=0时)的温度,又因为钢厂在实际生产中采用的是保护浇注,无法精准测量其温度,故将浇铸温度等效为结晶器弯月面处的温度。
1.4 边界条件铸坯在整个凝固过程中的传热,自上而下分别经过结晶器、二冷区和空冷区进行热量交换。因不同阶段换热条件随冷却区域的不同而变化,则各冷却区域的边界条件如下:
1)结晶器边界条件
结晶器的边界条件使用瞬时热流密度来表示,瞬时热流密度的计算公式为[12]:
| $ Q=2680000-B\sqrt{{{L}_{\text{m}}}/V} $ | (2) |
| $ B=N\times (2680000-{{q}_{\text{m}}})/\sqrt{L/V} $ | (3) |
式(2)、式(3)中:Lm为距弯月面距离,m;
| $ {{q}_{\text{m}}}={{C}_{\text{w}}}{{q}_{\text{w}}}{{\rho }_{\text{w}}}\Delta {{T}_{\text{w}}}/{{F}_{\text{eff}}} $ | (4) |
式(4)中:
2)二冷区边界条件
在二冷区,边界条件通常以二冷区热流密度(q)来计算[13]:
| $ q=h\cdot ({{T}_{\text{b}}}-{{T}_{\text{w}}}) $ | (5) |
| $ h=a\cdot {W}^{n} $ | (6) |
式(5)、式(6)中:
3)空冷区边界条件
| $ {q}_{a}=\epsilon \sigma \left[\right(273+T{)}^{4}-(273+{T}_{0}{)}^{4}] $ | (7) |
式中:qa辐射热流密度,W/m2; ε为铸坯表面黑度,取0.8;
运用UG画图软件建立了薄片模型,将所建模型导入至ProCAST软件中的MeshCAST模块中, 进行面网格和体网格的划分, 综合考虑了计算的精读性和时间后, 将其薄片的厚度设定为10 mm, 则模型的大小确定为200×200×10(mm),所划面的网格个数为4364,体网格数为26493,如图 1所示。
2.2 计算参数确定在ProCAST软件的材料数据库模块中对模拟的钢种20CrMnTi化学成分进行自定义,详见表 1。通过模拟软件中的Lever定律模型计算可得到20CrMnTi的液相线温度、固相线温度(见表 2)以及热导率、密度、热焓和固相率与温度的关系,如图 2所示。根据表 3中方坯连铸的生产工艺参数,应用式(2)~(7)则可计算出薄片在各个冷却段的热流密度和换热系数,见表 4,再由拉速可确定铸坯在各冷却段停留时间,最后在程序中输入相应数据就可得到冷却条件与时间关系的曲线。
|
|
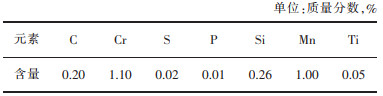
表 1 模拟钢种20CrMnTi的化学成分 |
|
|
表 2 模拟钢种20CrMnTi的固液相线温度 |
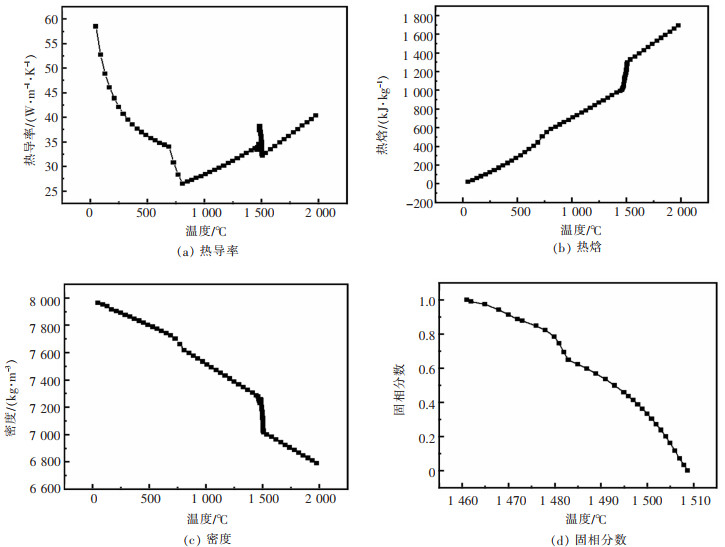 |
| 图 2 20CrMnTi的热物理参数随温度变化 |
|
|
表 3 模拟钢种20CrMnTi的生产工艺参数 |
|
|
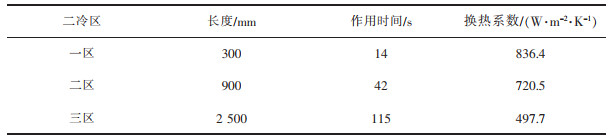
表 4 冷却参数和作用时间 |
图 2(a)~图 2(d)分别为20CrMnTi在凝固过程中热导率、热焓、密度、固相分数随温度的变化曲线。由图 2(a)可知,热导率随温度的升高先降低再增加,在730℃时,热导率达到最低值。由图 2(b)可知,热焓随温度的增加而增加,在1980 ℃时,最大值为1694 kJ/kg。由图 2(c)可知,铸坯的密度随温度的升高而降低,在1980 ℃时,密度最小为6789 kg/m3。由图 2(d)可知, 随着温度的降低,铸坯不断凝固,其固相分数不断增加,当固相分数为1时,则凝固完成。
模拟参数确定后,设定特定的模拟步长进行模拟计算。模拟计算完成后从ProCAST软件的后处理模块Viewer中就可得铸坯的表面温度、中心温度、中心固相率和液芯长度在凝固过程中的变化规律。
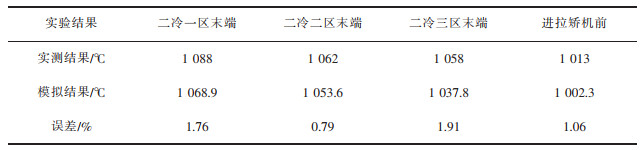
2.3 模型工业验证为了使模型能够准确反映工业生产实际情况,用红外测温枪对铸坯的某些位置表面温度进行测定,然后与模拟该位置处所得表面温度进行对比分析,以对所建模型进行工业验证。测量对比结果如表 5所示。由表 5可得,铸坯各位置表面温度的模拟结果和工业实测结果相对误差均小于2%,在工业误差5%允许范围之内,所以本文建立的凝固传热数学模型能够较准确的预测方坯凝固过程。
|
|
表 5 模拟表面温度与实测表面温度结果对比 |
在拉速为1.3 m/min、二冷水量分别为76、71、47 L/min的条件下,模拟过热度分别为30、20、10 ℃时对方坯表面温度、中心温度、中心固相率及液芯长度的影响;在过热度30 ℃、二冷水量分别为76、71、47 L/min的条件下,模拟拉速分别为1.3、1.2、1.1 m/min时对方坯表面温度、中心温度、中心固相率及液芯长度的影响;在拉速为1.3 m/min、过热度30 ℃条件下,研究不同二冷水量对方坯表面温度、中心温度、中心固相率及液芯长度的影响并考虑到现场实际生产条件,现将二冷水量调整为原来(76、71、47 L/min)的0.8倍(60.8、56.8、37.6 L/min)和1.3倍(98.8、92.3、61.1 L/min)。具体实验方案详见表 6。
|
|
表 6 模拟实验方案 |
图 3分别给出了在拉速为1.3 m/min、二冷水量分别为76、71、47 L/min的条件下,不同过热度对方坯表面温度、中心温度、中心固相率及液芯长度的影响。
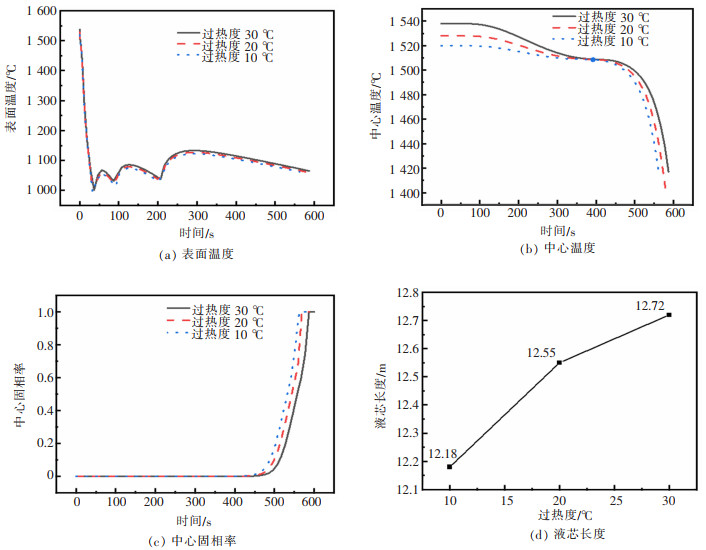 |
| 图 3 钢液过热度对方坯凝固过程的影响 |
由图 3(a)可知,过热度对铸坯的表面温度及表面回温影响较小,过热度越大,表面温度越高。过热度每增加10 ℃,二冷三区末端铸坯的表面温度平均大约增加8 ℃。进拉矫机前铸坯的表面温度大于900 ℃,则可保证在拉矫过程中具有良好的塑性。由图 3(b)可知,过热度对浇注前期和二冷区之后铸坯的中心温度影响较大,对二冷一区、二区、三区末端中心温度变化影响很小,这是因为由于时间较短热量传递还未到达铸坯中心。由图 3(c)可知,随着过热度的增加,固液两相区的起始位置及凝固终点位置均向后延伸。过热度由10 ℃分别增加到20 ℃、30 ℃时,固液两相区的起始位置分别向后延伸了0.58 m和0.39 m, 凝固终点位置分别向后延伸了0.37 m和0.17 m。由图 3(d)可知,随着过热度的增加,液芯长度逐渐增加,每增加10 ℃,液芯长度由原来的12.18 m分别增加到12.55 m和12.72 m。
3.2 铸坯拉坯速度对方坯凝固过程的影响图 4分别给出了在过热度为30 ℃、二冷水量分别为76、71、47 L/min的条件下不同拉速对方坯表面温度、中心温度、中心固相率及液芯长度的影响。
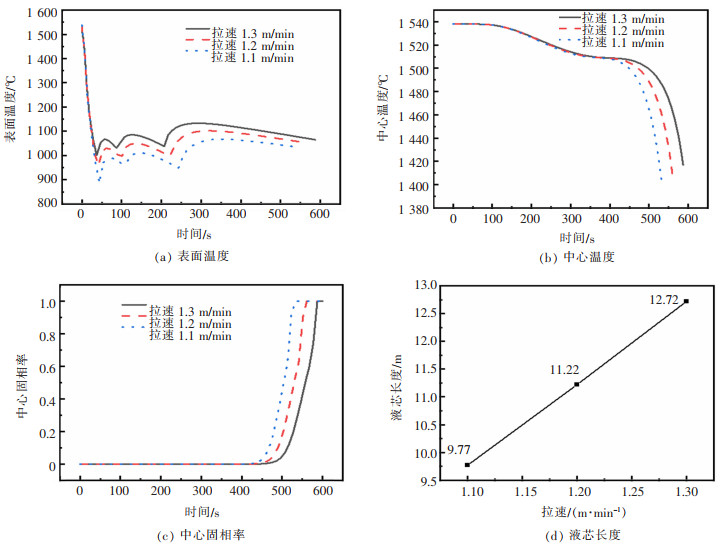 |
| 图 4 铸坯拉速对方坯凝固过程的影响 |
由图 4(a)可知,拉速对铸坯表面温度影响很大,拉速越高,表面温度越高;当拉速每增加0.1 m/min时,二冷区各冷却段的表面温度增加25℃左右,这是因为在不改变其它连铸工艺参数的情况下,改变拉速,会造成铸坯在二冷区各区域二冷水量的改变,进而影响了铸坯的表面温度。由图 4(b)可知,拉速对铸坯中心温度的影响主要在二冷区以后,当拉速每增加0.1 m/min时,进拉矫机前中心温度增加30 ℃左右;拉速对二冷区各段中心温度影响很小,一般在5 ℃以内。由图 4(c)可知, 随着拉速的增加,固液两相区的起始位置及凝固终点位置均向后延伸。拉速由1.1 m/min分别增加到1.2m/min、1.3 m/min时,固液两相区的起始位置分别向后延伸了0.83 m和1.03 m;凝固终点位置分别向后延长了1.45 m和1.5 m。由图 4(d)可知,随着拉速的增加,液芯长度逐渐增加,每增加0.1 m/min,液芯长度由原来的9.77 m分别增加到11.22 m和12.72 m。
3.3 二冷区冷却水量对方坯凝固过程的影响图 5分别给出了在过热度为30 ℃、拉速为1.3 m/min条件下,不同二冷水量对方坯表面温度、中心温度、中心固相率及液芯长度的影响。
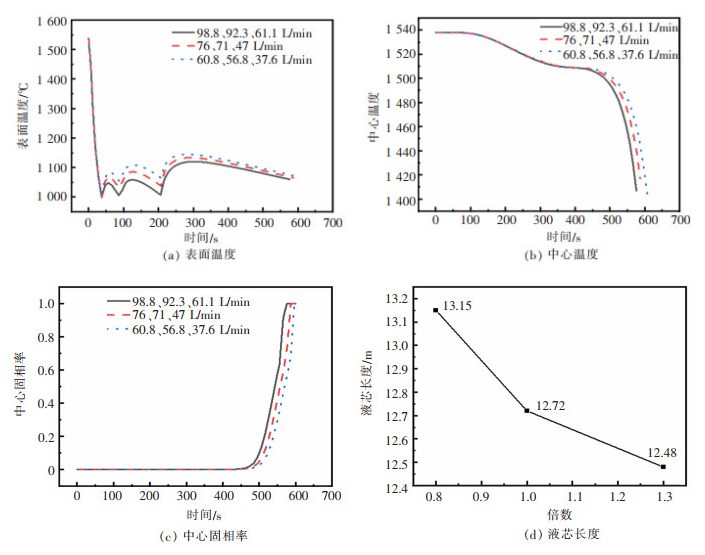 |
| 图 5 冷却水量对方坯凝固过程的影响 |
由图 5(a)可知,铸坯的表面温度随着二冷水量的增加而降低。当二冷水量增加为原来的1.3倍时,铸坯在二冷一区、二冷二区的表面温度降低20℃左右,在二冷三区表面温度降低35 ℃左右;当二冷水量降低为原来的0.8倍时,铸坯在二冷一区、二冷二区的表面温度增加20 ℃左右,在二冷三区表面温度增加30 ℃左右。由图 5(b)可知,二冷水量对铸坯中心温度的影响主要也在二冷区以后,中心温度随二冷水量的增加而降低;当冷却水量增加为原来的1.3倍时,进拉矫机前的中心温度降低了15 ℃左右;二冷水量对二冷区各段中心温度影响较小,在7 ℃以内。由图 5(c)可知,固液两相区的起始位置和凝固终点位置随着冷却水量的增加而缩短、降低而延长。当冷却水量增加为原来的1.3倍时,固液两相区的起始位置缩短了0.24 m;当冷却水量降低为原来的0.8倍时,固液两相区的起始位置延长了0.22 m。由图 5(d)可知,液芯长度随着冷却水量的增加而缩短、降低而延长。当冷却水量增加为原来的1.3倍时,液芯长度由原来的12.72 m缩短为12.48 m;当冷却水量降低为原来的0.8倍时,液芯长度由原来的12.72 m增加为13.15 m。
4 结论(1)过热度对铸坯的表面温度影响不大,过热度越高,表面温度越高;过热度每增加10℃,铸坯出二冷区时的表面温度约增加8℃;过热度对铸坯中心温度的影响主要在浇铸前和二冷区之后;随着过热度的增加,固液两相区的起始位置和凝固终点位置均有所延长,同时液芯长度也增加。
(2)拉速对铸坯的表面温度影响很大,拉速越高,表面温度越高;当拉速每增加0.1 m/min时,二冷区各冷却段的表面温度增加25℃左右;进拉矫机前中心温度增加30℃左右;固液两相区的起始位置分别向后延长了0.83 m和1.03 m;液芯长度由原来的9.77 m分别增加到11.22 m和12.72 m。
(3)铸坯的表面温度随冷却水量的增加而降低,当冷却水量增加为原来的1.3倍时,铸坯在二冷一区、二冷二区的表面温度降低20℃左右,在二冷三区表面温度降低35℃左右;对铸坯中心温度的影响主要也在二冷区以后,中心温度随二冷水量的增加而降低;固液两相区的起始位置和凝固终点位置及液芯长度随着冷却水量的增加而缩短、降低而延长。
| [1] |
吴强, 李巩. 汽车渗碳齿轮用钢及热处理工艺的现状和发展趋势[J]. 科技展望, 2016, 26(30): 43. DOI:10.3969/j.issn.1672-8289.2016.30.039 |
| [2] |
吴树漂, 刘占江, 武云峰, 等. 我国齿轮钢的生产与应用[J]. 特殊钢, 2003, 24(5): 30-33. DOI:10.3969/j.issn.1003-8620.2003.05.010 |
| [3] |
张振学, 张慧, 王明林, 等. GCr15轴承钢大方坯连铸过程凝固传热数值模拟[J]. 铸造技术, 2019, 40(8): 763-767. |
| [4] |
铁占鹏, 王宝峰, 高志冉, 等. 20CrMnTi连铸大方坯凝固规律的模拟计算[J]. 连铸, 2014, 39(3): 43-48. |
| [5] |
李璐, 周存龙, 刘丽晶, 等. HRB400钢热物性参数对小方坯连铸凝固传热模型影响的研究[J]. 连铸, 2019, 44(5): 14-20. |
| [6] |
YOON J K. Applications of numerical simulation to continuous casting technology[J]. ISIJ International, 2008, 48(7): 879-884. DOI:10.2355/isijinternational.48.879 |
| [7] |
LALLY B, BIEGLER L, HENEIN H. Finite difference heat-transfer modeling for continuous casting[J]. Metallurgical Transactions B, 1990, 21(4): 761-770. DOI:10.1007/BF02654255 |
| [8] |
TIEU A K, KIM I S. Simulation of the continuous casting process by a mathematical model[J]. International Journal of Mechanical Sciences, 1997, 39(2): 185-192. |
| [9] |
李茂印, 杨树峰, 李京社, 等. 45#钢连铸坯凝固过程数值模拟与验证[J]. 工业加热, 2017, 46(6): 25-28. |
| [10] |
孙涛, 岳峰, 郭春, 等. C45Cr钢连铸大断面圆坯凝固过程数学模拟[J]. 铸造技术, 2015, 36(7): 1820-1825. |
| [11] |
李璐. 连铸方坯凝固传热数值模拟及铸坯升温工艺探究[D]. 太原: 太原科技大学, 2020.
|
| [12] |
王晓连, 王新华, 李林平, 等. 高拉速下板坯连铸结晶器铜板传热行为研究[J]. 炼钢, 2014, 30(3): 54-59. |
| [13] |
MORALES R D, LóPEZ A G, OLIVARES I M. Heat transfer analysis during water spray cooling of steel rods[J]. ISIJ International, 1990, 30(1): 48-57. |
| [14] |
CABRERA-MARRERO J M, CARREÑO-GALINDO V, MORALES R D, et al. Macro-micro modeling of the dendritic microstructure of steel billets processed by continuous casting[J]. ISIJ International, 1998, 38(8): 812-821. |
| [15] |
WANG Q Q, ZHANG L F. Influence of FC-mold on the full solidification of continuous casting slab[J]. JOM, 2016, 68(8): 2170-2179. |
 2021, Vol. 41
2021, Vol. 41