| 使用圆孔透气塞的钢包内流场及其渣眼行为研究 |
2. 成都市力生实业有限责任公司,成都 610061
2. Chengdu Lisheng Industrial Co., Ltd., Chengdu, 610061, China
随着人们对物质生活要求的提高,高品质钢在工业经济中变得不可或缺。为了生产高品质钢,钢包底吹氩是目前使用最为广泛的一种炉外精炼技术[1],而此炉外精炼的关键性元件透气塞被安装在钢包底部。精炼过程中,经过预热和装钢之后,氩气通过透气塞吹入钢水中,在使钢水的成分和温度均匀的同时,也使钢水中的夹杂物粘附于气泡上从而上浮至渣层,经过等待后的钢水浇注于中间包内。整个精炼过程中,透气塞的冶炼效果与其钢包内的流场有着直接关系,特别是其渣眼行为决定了钢水的再次氧化以及卷渣效应的产生[2-5]。为了延长透气塞的使用寿命,采用圆孔狭缝代替矩形狭缝透气塞后发现,其混匀时间和夹杂物去除率明显提高[6],但是其流场以及渣眼行为缺乏进一步的研究论证。
过去的十年里,炉外精炼过程中钢包的流场以及混匀现象被广泛研究,这些研究往往采用水模试验和数值模拟的方法。许多前期研究多集中于钢液中气羽的形貌[7]、流量以及混匀行为[8-10],然而随着对钢水洁净度要求的提高,渣/钢液的界面的行为以及渣眼面积的研究也相对增多[11]。但是,在这众多的数值模拟研究中,都仅仅考虑了单一均匀的气泡尺寸,而气泡的凝并和破裂两因素都被忽略了。特别是在圆孔狭缝式透气塞中,狭缝尺寸对气泡大小具有直接影响[12]。因此,本文主要采用离散相模型耦合VOF模型来研究圆孔透气塞在精炼过程中钢包内的流场以及渣眼行为[13-15],此研究模型不仅可以描述气泡在钢水中的凝并和破裂等现象,还可以得到渣/钢液的界面运动。
1 数值模型在钢包底吹氩气炉外精炼的过程中,钢包中除了有钢水这一液相外,还有液相钢渣和气相氩气,钢水中还存在气泡,属于典型的多相流。本文使用商业软件Fluent中的多相流与离散相模型对钢包底吹氩气过程进行模拟,气泡以离散相形式持续入射到流场中,与连续相进行相间耦合计算,并考虑气泡的碰撞、合并与破碎。由于离散相模型的使用限制为颗粒相,体积要远小于网格体积,当气泡入射到流场中后不断地发生碰撞、合并过程,使得气泡体积逐渐增大,当离散相的气泡颗粒体积与该位置网格体积相当时,离散相模型不再适用于求解之后的气泡运动过程,这时则需要利用用户自定义方式(UDF)删除该离散相气泡颗粒,并在流场中生成一个同体积的连续相实体气泡代替离散相进行计算。这种方式简化了几何建模和空间离散过程,网格数量可以控制到80 000以内,时间步长可设置到0.05 s左右,使得数小时内即可完成1个工况的计算,大大降低了计算成本。
本文采用的1/2模型计算域划分成86 700个单元网格,其网格划分情况和坐标系如图 1所示。1/2透气砖模型中包含16个孔位,对应16束惯性颗粒,具体入射位置见表 1,通过模拟计算得到不同流量情况下钢包水模型内的流动过程,计算采用物性参数表 2,此外还采用了课题组水模试验平台验证数模计算的准确性,实验过程中采用的工程参数与实际钢包吹氩过程的工程参数如文献[16]所示。
 |
| 图 1 钢包计算域网格 |
|
|
表 1 粒子束喷射位置 |
|
|
表 2 水模与数模用材料参数 |
Fluent中通过积分拉氏坐标系下的颗粒作用力微分方程来求解离散相颗粒(颗粒或气泡)的轨迹。在笛卡尔坐标系下颗粒的作用力平衡方程可表示为:
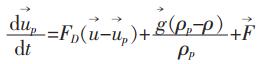
|
(1) |
式(1)中,FD(u-up)为颗粒的单位质量曳力;F为加速项。
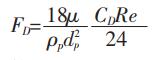
|
(2) |
式(2)中,u为流体相速度,m/s; up为颗粒速度,m/s;ρ为流体密度,kg/m3;ρp为颗粒密度,kg/m3; dp为颗粒直径,mm; Re为颗粒雷诺数。
本文假设气泡为球形,其曳力如文献[17]计算,其中包含真实质量力和压力梯度的力的额外加速项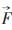
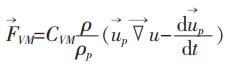
|
(3) |
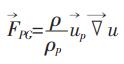
|
(4) |
式(3)中,CVM为真实质量系数,值为0.5。
1.2 VOF模型本文采用VOF模型追踪钢液、渣层和空气之间的自由液面,该界面采用求解各相体积分数的连续性方程实现,其单元体积分数描述如下:
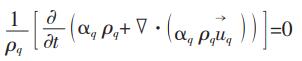
|
(5) |
式(5)中,αq为第q相的体积分数,且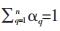
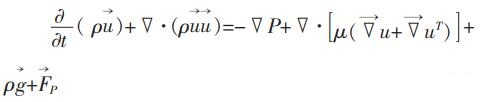
|
(6) |
式(6)中,ρ和u为混合相密度,kg/m3; g为重力加速度;p为压强,Pa; 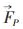
本文的模型中采用O'ROURKE[18-19]算法来计算气泡的凝并现象,即采用随机的方法来估计碰撞概率。假定只有颗粒组同存于一个流体网格内,碰撞才可能发生。实际生产中底吹钢包内的物理化学过程是非常复杂的,为了便于研究,计算过程不考虑钢渣之间化学反应的影响和传热现象,假设模型中的离散相气泡的形状不变化,因此,可以采用颗粒组方式计算离散相间的碰撞和合并,颗粒组代表数量根据质量流率计算,将等效粒径作为不同流量下离散相气泡的直径大小。
2 结果与讨论 2.1 气泡行为分析水模实验中使用HXLin64高速摄像机以2 000帧/秒的速度对底吹过程中气泡的运动情况进行了拍摄,如图 2为距离透气砖出口70 mm可以看到气泡在上升的过程中碰撞到一起,气泡凝并成一个气泡继续上升。
 |
| 图 2 实际气泡凝并 |
如图 3中(a)、(b)、(c)分别为2.020、2.022 s和2.026 s时距离透气砖出口50 mm处数学模拟结果。在该气泡束中,不仅可以看到两个小气泡接触之后的凝并然后其直径变大的凝并过程,而且该过程主要发生在距离透气砖顶端0.2 m以内,整个吹氩过程中最大气泡直径为3.2 mm。对比图 2和图 3,说明该DPM-VOF模型可以较好地描述钢包中实际气泡的凝并现象。
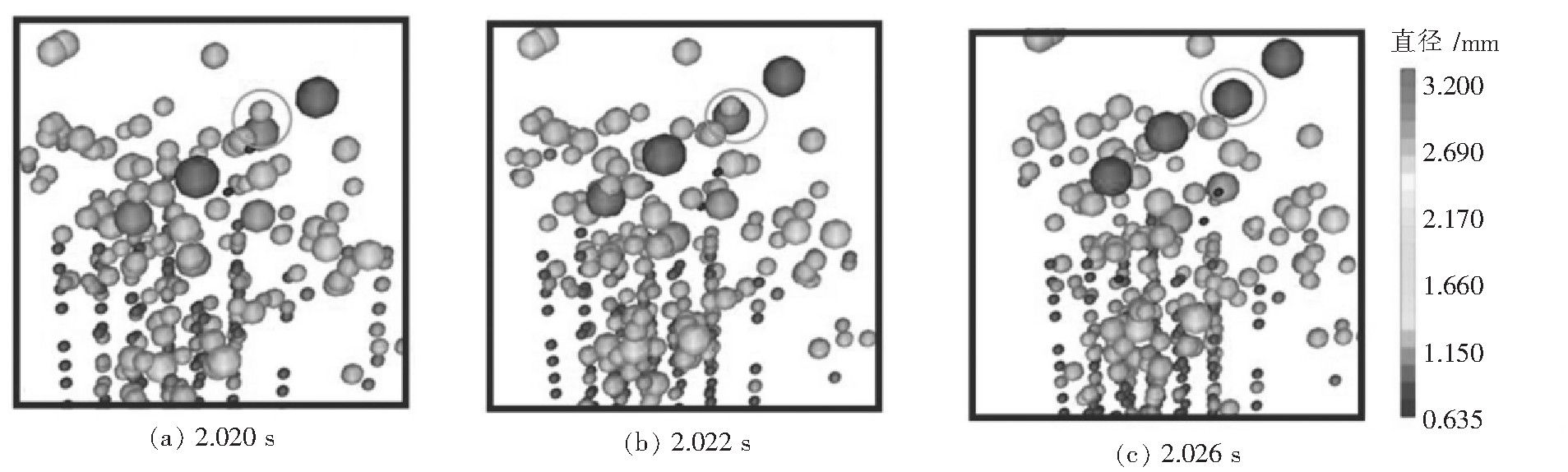 |
| 图 3 计算气泡凝并 |
不同底吹流量吹气60 s时对称面的流线图如图 4所示,随着底吹流量的增大,钢包内的流动形态变化不大。氩气从钢包底部的喷嘴喷入钢包,在惯性力和浮力的共同作用下,带动钢液形成倒锥形上升流股,随着气流的上升,液体的流动速度不断增大,相应地,流股内的压力减小,周围的液体不断被吸入,这种卷吸作用下形成气、液两相流,当气液两相区形成的上升流到达熔池液面后,气体溢出熔池,钢液被带动到一定的高度,钢液由于惯性力的作用从中心向外流向包壁,并在靠近包壁处向下流动,最后又被中心上升流抽引,从而形成一大一小的两个循环流。
 |
| 图 4 T=60 s时不同吹气流量下的流线图 |
由图 4可知,底吹流量为0.7 L/min时,此时底吹流量小,带动的钢水的动能较小,渣层没有被吹开,钢水环流速度较慢,环流的角速度也较小,此时距离透气砖较远一侧的环流中心更靠近钢包中部;底吹流量为2.25 L/min时,一部分钢水的动能在渣眼处做功消耗,渣层被吹开,形成渣眼,此时底吹流量较大,钢水环流速度较快,环流角速度更大,此时距离透气砖较远一侧的环流中心贴在被吹开的渣眼边缘;底吹流量大于2.25 L/min时与之类似,渣层被吹开,随着流量的增加,用来推动钢水水平运动做功的能量逐渐饱和,大部分钢水的动能在渣眼处做功消耗溢出,钢水环流速度较快,此时距离透气砖较远一侧的环流中心始终保持在渣眼边缘。
图 5是不同底吹流量下吹气60 s时对称面上的最大速度,当底吹流量高于3.76 L/min时,底吹流量的增大时钢液的流速在一个范围内波动,当流量低于3.76 L/min时,底吹流量的增大,钢液流速增加明显;钢液流速越快,钢液混匀时间就越短,这与水模实验结果吻合。
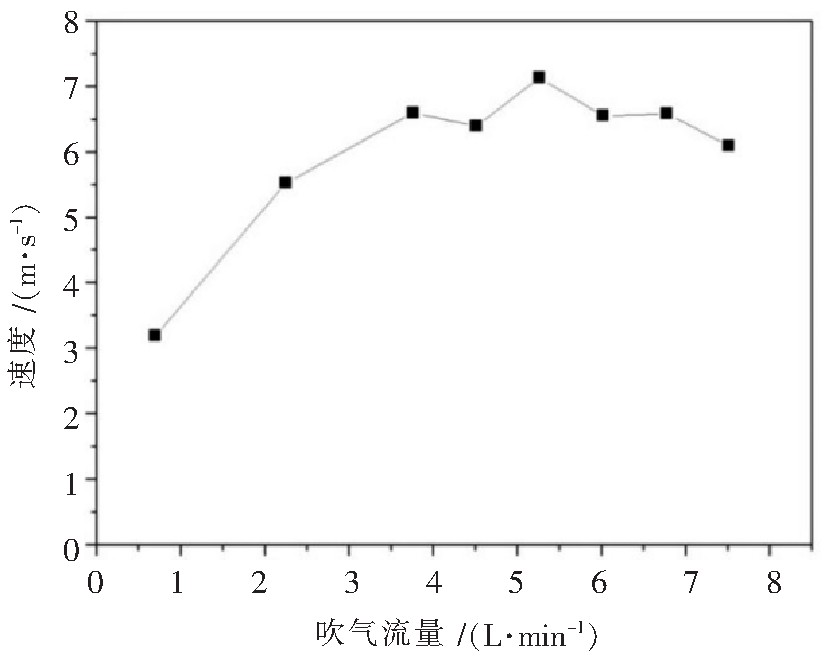 |
| 图 5 T=60 s时不同流量下钢水最大速度 |
图 6为不同底吹流量下吹气60 s时的对称面上的速度分布图,不同流量虽然没有改变钢液的流动形态,但是随着流量的增加,钢液的流动速度发生了改变,速度最大的位置为气泡带动钢液流动上升的气液两相区,当气泡冲出液面之后钢水的速度由竖直向上变为水平方向。
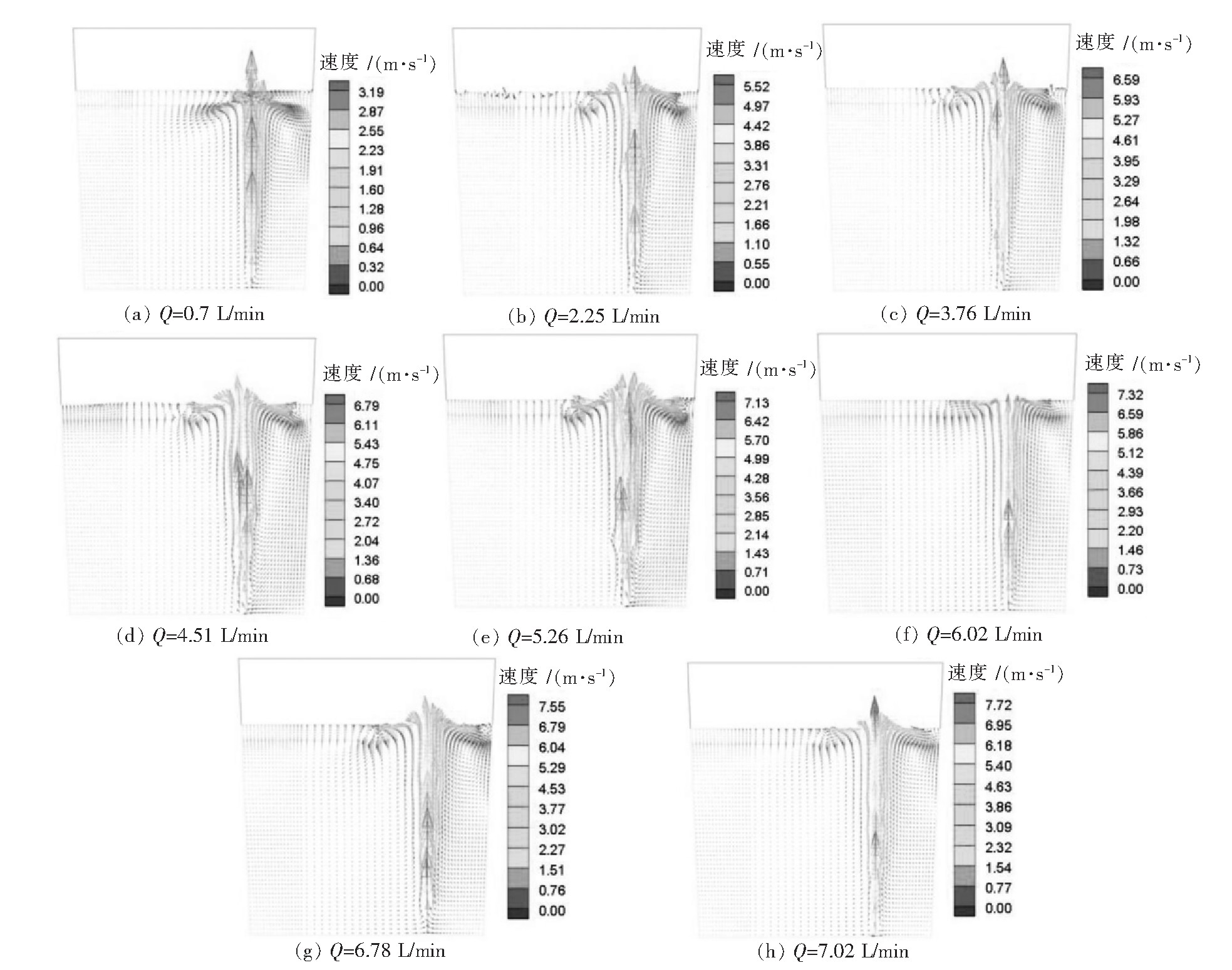 |
| 图 6 T=60 s时不同吹气流量下对称面的速度分布 |
在钢包底吹的实际工艺过程中,钢渣的存在具有两面性,它对脱硫、脱碳及去除夹杂物等起着非常积极的作用,但是也可能因为卷渣而降低钢坯的质量。因此,研究渣眼形态及大小有着重要的作用。
如图 7为底吹流量为2.25 L/min到7.51 L/min时的数值模拟计算的渣眼,随着底吹流量的增大,渣眼面积的变化趋势与实际情况相符,都是逐渐增大。与实验结果对比如图 8所示,当底吹流量低于3.76 L/min时,模拟的渣眼面积比实验值略小,当底吹流量大于3.76 L/min时,模拟的渣眼面积比实验值大,最大误差在15%以内,由此可以认定数值模拟结果与实际水模实验数据比较吻合,验证了数学模型的正确性。
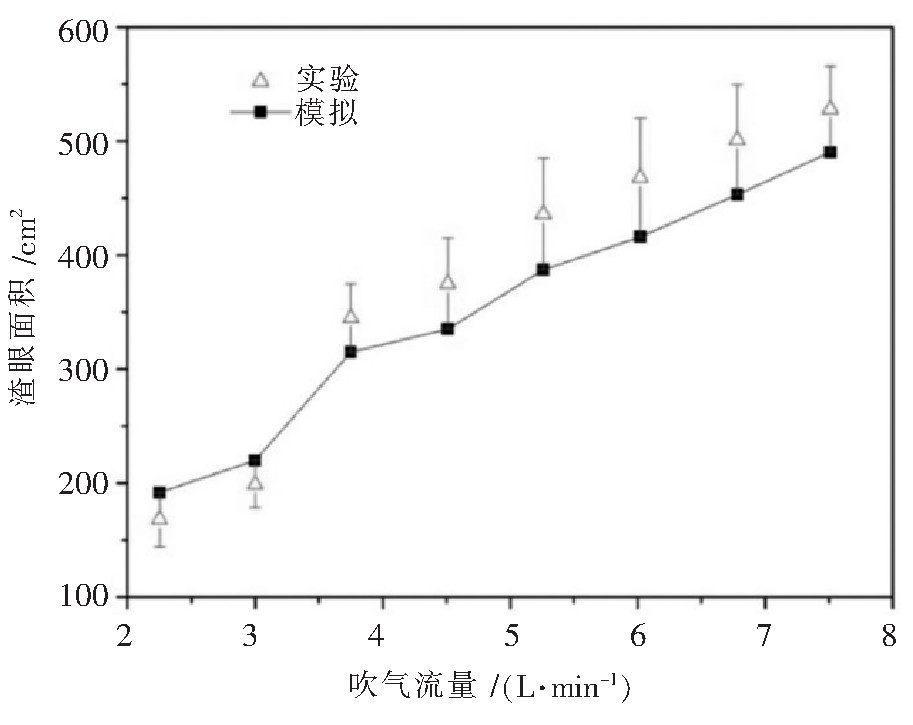 |
| 图 7 水模实验和数学模拟渣眼面积 |
 |
| 图 8 T=60 s时不同流量下的渣眼 |
采用考虑气泡凝并的数值模拟方法,研究了使用圆孔透气塞的钢包吹氩过程,对比了不同流量下钢包内的流场以及渣眼行为。数值计算的结果表明,底吹气体流量对钢包的流场特征影响不大,当流量高于3.76 L/min时,流量的增大对钢液的流速影响不大,当底吹流量低于3.76 L/min时,流量增大,钢液流速增大;计算结果再现了气泡凝并的过程,且气泡凝并主要发生在距离透气砖顶端0.2 m以内;计算结果的渣眼面积改变与水模实验的渣眼面积改变吻合得比较好,验证了数学模型的正确性。
| [1] |
LIU H, QI Z, XU M. Numerical simulation of fluid flow and interfacial behavior in three-phase argon-stirred ladles with one plug and dual plugs[J]. Steel Research International, 2011, 82(4): 440-458. DOI:10.1002/srin.201000164 |
| [2] |
ZH ANG L, AOKI J, THOMAS B G. Inclusion removal by bubble flotation in a continuous casting mold[J]. Metallurgical and Materials Transactions B, 2006, 37(3): 361-379. DOI:10.1007/s11663-006-0021-z |
| [3] |
KANG Y J, YU L, SICHEN D. Study of inclusion removal mechanism around open eye in ladle treatment[J]. Ironmaking & Steelmaking, 2007, 34(3): 253-261. |
| [4] |
CHATTOPADHYAY K, SENGUPTA A, AJMANI S K, et al. Optimisation of dual purging location for better mixing in ladle: A water model study[J]. Ironmaking & Steelmaking, 2009, 36(7): 537-542. |
| [5] |
KHAJAVI L T, BARATI M. Cold model study of emulsification behavior in bottom blown metallurgical baths covered with thick slag[J]. ISIJ International, 2010, 50(5): 654-662. DOI:10.2355/isijinternational.50.654 |
| [6] |
卢寅寅, 谭方关, 贺铸, 等. 底吹钢包用圆孔透气砖冶金效果的水模型[J]. 材料与冶金学报, 2014, 18(1): 41-48. |
| [7] |
MAZUMDAR D, EVANS J W. A model for estimating exposed plume eye area in steel refining ladles covered with thin slag[J]. Metallurgical and Materials Transactions B, 2004, 35(2): 400-404. DOI:10.1007/s11663-004-0041-5 |
| [8] |
CO NEJO A N, KITAMURA S, MARUOKA N, et al. Effects of top layer, nozzle arrangement, and gas flow rate on mixing time in agitated ladles by bottom gas injection[J]. Metallurgical and Materials Transactions B, 2013, 44(4): 914-923. DOI:10.1007/s11663-013-9829-5 |
| [9] |
TERRAZAS M S C, CONEJO A N. Effect of nozzle diameter on mixing time during bottom-gas injection in metallurgical ladles[J]. Metallurgical and Materials Transactions B, 2014, 46(2): 711-718. |
| [10] |
TANG H Y, GUO X C, WU G H, et al. Effect of gas blown modes on mixing phenomena in a bottom stirring ladle with dual pl ugs[J]. ISIJ International, 2016, 56(12): 2161-2170. DOI:10.2355/isijinternational.ISIJINT-2016-360 |
| [11] |
LIU W, TANG H, YANG S, et al. Numerical simulation of slag eye formation and slag entrapment in a bottom-blown argonstirred ladle[J]. Metallurgical and Materials Transactions B, 2018, 49(5): 2681-2691. DOI:10.1007/s11663-018-1308-6 |
| [12] |
YUAN J, LI Y, WANG N, et al. Effect of orifice diameter on bubble generation process in melt gas injection to prepare aluminum foams[J]. Metallurgical and Materials Transactions B, 2016, 47(3): 1649-1660. DOI:10.1007/s11663-016-0638-5 |
| [13] |
LING H T, LI F, ZHANG L F, et al. Investigation on the effect of nozzle number on the recirculation rate and mixing time in the Rh process using VOF+DPM model[J]. Metallurgical and Materials Transactions B, 2016, 47(3): 1950-1961. DOI:10.1007/s11663-016-0669-y |
| [14] |
LING H, ZHANG L, LIU C. Effect of snorkel shape on the fluid flow during RH degassing process: mathematical modelling[J]. Ironmaking & Steelmaking, 2018, 45(2): 145-156. |
| [15] |
DUAN H, REN Y, ZHANG L. Fluid flow, thermal stratification, and inclusion motion during holding period in steel ladles[J]. Metallurgical and Materials Transactions B, 2019, 50(3): 1476-1489. DOI:10.1007/s11663-019-01535-x |
| [16] |
TAN F, HE Z, JIN S, et al. Physical modelling evaluation on refining effects of ladle with different purging plug designs[J]. Steel Research International, 2020, 10.1002/srin.201900606.
|
| [17] |
LIU A B, MATHER D, REITZ R D. Modeling the effects of drop drag and breakup on fuel sprays[M]. SAE International. 1993.
|
| [18] |
O'ROURKE P J. Los alamos national lab[M]. NM(USA): 1981.
|
| [19] |
LI L, LIU Z, CAO M, et al. Large eddy Simulation of bubbly flow and slag layer behavior in ladle with discrete phase model(DPM)-volume of fluid(VOF)coupled model[J]. JOM, 2015, 67(7): 1459-1467. DOI:10.1007/s11837-015-1465-x |
 2020, Vol. 40
2020, Vol. 40