| 融合光线追踪和中值滤波的深度图像修复算法 |
近年来,随着低成本消费级深度相机的不断普及,深度图像在物体三维建模[1-4]、目标跟踪[5-7]、目标识别与分割[8-10]等领域有着广泛的应用。但是,由于成像原理、环境、物体本身特性等因素的影响,采集的深度图像中存在离散的噪声点和一定范围的深度信息缺失现象。为此,国内外许多研究人员进行了大量的研究。
在深度图像空洞修复方面,目前主要通过传统的图像滤波和基于深度学习的方法进行空洞修复。Camplani等利用双边滤波(Bilateral Filter, BF)对深度图像空洞进行修复,根据空间距离和深度值进行高斯核加权滤波修复,能够修复小范围的空洞缺失区域,但对较大范围的空洞修复效果不佳,易造成图像模糊的情况[11]。Le等在双边滤波算法的基础上,使用彩色图像作为引导图,提出联合双边滤波算法(Joint Bilateral Filter, JBF),其修复效果有一定提升,但在边缘区域,其修复值与目标值仍存在较大的偏差,且需不断调整滤波参数以适应图像滤波的需要[12]。王得成等提出了自适应联合双边滤波算法,与固定的滤波参数不同的是,该算法能够根据空洞占比和图像的结构相似性自适应选择滤波参数值,在修复较大范围的空洞尤其是边缘附近的空洞时,易受边缘邻近物体深度值的影响,导致深度值产生一定的偏差, 修复效果不佳[13]。胡天佑等通过对彩色图像进行超像素分割,并根据空洞大小使用不同方法进行修复,但由于设定的超像素个数不同,其修复结果将产生不同程度的误差[14]。王殿伟等引入形态学滤波(Morphological Filter, MF)对空洞区域进行逐步修复,能够修复相对较平滑的区域,但对于深度值变化较大的区域,修复后出现块状过平滑现象,丢失了物体本身的细节特征[15]。Li等通过训练卷积网络模型的方法进行空洞修复,空洞修复效果较好,能够保留清晰的细节[16]。Zhang等利用深度学习的方法通过RGB图像预测深度图像的表面法线和边界值并结合已有的深度值进行修复,取得了很好的修复效果,但基于神经网络模型和深度学习的修复算法均需要大量的样本数据集进行训练和学习,且训练时间长,不适用于样本量小的深度图像修复[17]。
针对上述算法在深度图像空洞修复方面存在修复不佳、边缘模糊、细节特征缺失等问题,本文引入一种光线追踪算法——时空差异引导滤波算法[18],提出融合光线追踪和中值滤波算法对深度图像空洞进行修复。先通过时空差异引导滤波算法对深度图像的空洞区域进行修复,然后使用中值滤波对深度图像进行平滑和去噪,以保留深度图像的边缘信息和细节特征,从而达到修复面积较大的空洞区域的目的。
1 算法原理光线追踪算法可分为前向光线追踪和后向光线追踪[19]。前向追踪是模拟大量光线从光源出发,通过物体的反射进入人眼的成像过程。该过程需模拟发射大量光线,运算量大,对性能要求高,且仅有少量光线进入人眼,光线利用率低。后向光线追踪则是反向模拟进入人眼的少量光线,原理如图 1所示。该技术大大降低了计算量,提高了运行速率,且能够很好地模拟出物体表面的光照情况。
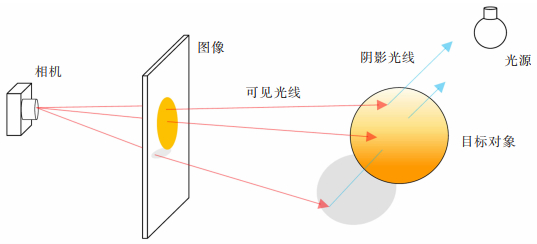 |
| 图 1 光线追踪原理 |
时空差异引导滤波算法是John Burgess等人于2017年发表在High Performance Graphic上的一种光线追踪渲染算法,主要用于计算机虚拟环境中的模型渲染降噪工作,其目的是在输入图像中像素样本非常少的情况下,能够将图像还原到与目标图像质量接近的程度。本文将时空差异引导滤波算法引入对深度图像的空洞修复,通过构建路径跟踪器将光分解成直接光照和间接光照,然后分别进行处理。根据多帧历史深度图像数据对当前帧深度图像进行时空滤波、方差估计、色彩映射和抗锯齿化等操作,最后使用中值滤波平滑图像。其算法流程如图 2所示。
 |
| 图 2 本文算法流程 |
构建一个带光栅化器和无噪声G缓冲器的路径跟踪器,其中光栅化器用于生成主射线,G缓冲器包含重建滤波器的附加表面属性:深度、空间法线、网格索引、栅格化空间矢量等,为后续的时间滤波和空间滤波提供滤波参数。通过构建的路径跟踪器对每个像素点生成1个深度样本,并进行路径空间正则化[20]处理,以增加深度图像表面粗糙度,使得路径跟踪器能追踪到光源位置。将追踪的光线分别输出为直接光照和间接光照,通过重建滤波器分别计算其局部平滑度,以更好地重采样效果较差的深度图像边缘。然后从深度样本中解调包含纹理和空间变化的物体表面的直接光照反射率,过滤未纹理化或过度模糊的照明分量,在重建后重新应用纹理化,增加相邻样本的空间重复利用率。对于多次反射,增加每个物体的反射率,并按采样概率进行加权计算。
1.2 时空滤波时空差异引导滤波算法主要由时间滤波、方差估计和空间滤波组成。历史帧深度图像与当前帧深度图像通过时间和深度值空间的集成进行方差估计,并对结果进行多次小波滤波降噪,直到满足精度要求为止,其原理如图 3所示。
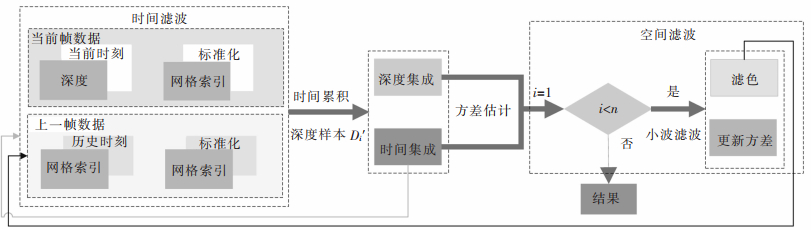 |
| 图 3 时空滤波流程 |
1)时间滤波
时间滤波的主要原理为:根据第i-1帧深度图像历史缓冲区中积累的多帧历史深度图像在某一位置的深度样本,并通过二维运动矢量将第i帧深度图像上的深度样本Di投影到第i-1帧深度图像的对应深度样本Di-1位置,然后对Di和Di-1的样本深度、空间法线、网格索引等属性值进行一致性比较。根据一致性比较结果,确定采集的两帧影像是否位于同一个坐标系中,然后利用指数移动平均值法将一致的深度样本Di'累积为新的深度样本,其计算公式如下:
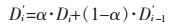
|
(1) |
其中,α用于控制时间衰减,将整体的时间稳定性滞后。当α取值为0.2时,实验效果最佳。
为了提高历史帧深度图像质量,采用滤波窗口大小为2×2的双边滤波对第i-1帧深度图像的深度样本Di-1进行重采样处理,检查每一个深度样本Di-1的反射投影深度、法线和网格索引等属性。若某个属性存在不一致的情况,则将该属性舍去,并将其权重值重新分配到其他一致的属性中;若所有的属性都不一致,则滤波窗口扩大为3×3,再进行属性一致性比较;若扩大滤波窗口后的所有属性仍不一致,则将该深度样本舍去,并用当前帧(第i帧)深度图像同一位置的深度样本Di代替。
2)方差估计
方差估计,主要是针对深度图像稀疏采样的嘈杂噪声区域进行处理,通过对动态采集的多帧深度图像进行分析,以检测时间累积下样本的可靠性。
为了有效地进行方差估计,使用当前时刻亮度值μNi和前一时刻亮度值μBi估算每一个深度样本的亮度方差,并使用几何一致性检验方法对方差进行积累,以估算当前帧深度样本的方差δi2,其公式如下:

|
(2) |
根据深度图像的深度样本的方差估计值,空间滤波能够自适应地对不同大小的边缘处噪声区域进行有效的修复。
3)空间滤波
为了保留深度图像的边缘细节清晰,本文采用基于5×5交叉双边滤波器的à-trous小波变换[21]对深度图像进行分层采样,并根据G缓冲器中的属性对图像中物体表面边缘进行识别。其中,à-trous小波变换算法的主要思想为:当i=1时,输入第一帧深度图像D1(p);对于后续采集的第i+1帧图像,根据第i帧深度图像信息进行离散卷积计算,并迭代N次,每迭代一次增大其离散卷积的距离为2N,由于每次迭代都会增加运算空间,同时为了保证修复的有效性,N取值为5,最后输出经滤波后的深度图像;将第一个小波迭代后的颜色输出,并作为历史深度,用于与后续采集的深度图像进行积分。
在上述算法中,进行离散卷积的计算公式为:
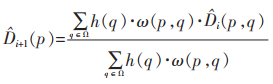
|
(3) |
其中,h是空间滤波的卷积核, 其值为: 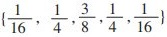
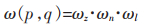
|
(4) |
对于深度变量ωz,假设深度图像中的物体表面深度呈局部线性模型关系,通过测量其与图像空间的偏差,并根据图像的空间偏导数来估计局部深度模型,得出ωz的表达式如下:
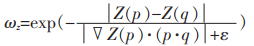
|
(5) |
其中,▽Z(p)是像素对应的深度相对于空间坐标的梯度;ε是一个非常小的值,其作用是避免表达式出现分母为零的情况。
空间法线权重函数ωn采用余弦项进行定义,即:
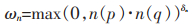
|
(6) |
其中,n(p)是深度样本p的输入法线;n(q)为邻域深度样本q的输入法线;参数δn的取值为128。
对于亮度权重函数ωl,利用3×3的高斯滤波核并结合亮度li(p)进行定义:
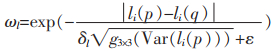
|
(7) |
其中,li(p)为中心深度样本p的亮度;li(q)为邻域深度样本q的亮度;δl的取值为4。
1.3 后期处理经上述时空滤波处理后,将处理后的深度图像依次进行色调映射、抗锯齿化。根据处理后的深度图像全局亮度推算出其平均亮度值,再根据平均亮度值选取一个合适的亮度域,再将整个深度图像深度样本映射到这个亮度域,得到新的深度图像。然后进行抗锯齿化处理[22],以提高时间稳定性,并对重建的几何边缘进行滤波混叠处理。
由于处理后的深度图像仍存在小范围的空洞和离散噪声点,而中值滤波是一种非线性的滤波方法,在平滑离散噪声的同时,保持图像边缘轮廓的清晰。其原理是用待修复点的邻域像素点深度值的中值代替待修复点的深度值,从而达到平滑图像和保持边缘特性的目的。为此,本文采用中值滤波算法对处理后的深度图像进行进一步的去噪平滑处理,其表达式如下所示:
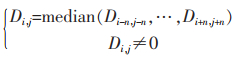
|
(8) |
其中,i、j分别表示待修复点的x、y轴方向的坐标值;此处的n=3,即采用滤波窗口大小为7×7的中值滤波进行滤波处理,得到最终的深度图像。
2 实验过程为了验证本文算法的优越性,采用小觅双目深度相机自行采集办公桌、窗帘、电梯门3个场景下连续多帧深度图像作为实验数据,分别命名为场景1、场景2、场景3。采用自适应模型修复的深度图作为基准图像,将本文算法与经典的双边滤波算法、联合双边滤波算法、形态学滤波算法的修复效果分别进行定性和定量比较。
本文实验是在CPU为i5-9300 H、系统为Windows 10系统的电脑上进行运算处理,并在Visual Studio 2017软件及Opencv库环境下进行编译和数据处理。在保证深度图像的物体边缘尽量清晰并且修复效果相对较好的情况下,本文将双边滤波和联合双边算法的滤波窗口大小ω设置为14,方差δs和δr分别设置为108和121。在窗帘和电梯门场景中,形态学滤波中膨胀和腐蚀迭代次数设置为23次,办公桌场景中迭代次数设置为9次。各种算法修复后的实验效果及基准图像如图 4-图 6所示。
 |
| 图 4 场景1的修复结果 |
 |
| 图 5 场景2的修复结果 |
 |
| 图 6 场景3的修复结果 |
与上述算法在3个场景的深度图像修复效果相比,本文算法修复效果最佳。其中,双边滤波算法和联合双边滤波算法能够对小范围的空洞和离散噪声点进行修复,对于场景中范围较大的空洞区域,其修复效果不佳。相较于双边滤波算法,联合双边滤波算法的修复效果有一定的提升,但修复点的深度值与邻域像素的深度值仍存在较为明显的灰度差。形态学滤波算法主要通过膨胀和腐蚀等操作修复空洞,该算法能够较好地修复小范围的空洞和物体内部较大范围的空洞。但由于在膨胀过程中是向邻域膨胀,当空洞位于深度值变化较大位置时,如图 4场景1中窗帘左侧处和图 5场景2中办公桌面的空洞区域,修复后的深度图像均出现锯齿和块状区域,并且细节纹理信息丢失较为严重。本文提出的算法无论是对小范围的空洞,还是对较大范围的空洞区域均有较好的修复效果。同时,还能较好地保留物体的纹理细节,使修复后的图像能保持较为清晰的纹理轮廓。
3.2 定量分析为了定量地分析深度图像的空洞修复效果,本文采用峰值信噪比(Peak Signal to Noise Ratio, PSNR)和均方根误差(Root Mean Square Error, RMSE)对各种算法修复的效果进行量化比较。由于本文提出的方法是基于历史帧数据对当前帧数据进行深度图像滤波修复,使用以上两种评价指标进行评价时,缺乏完整图像作为基准图像。因此,本文采用修复效果较好但修复时间较长的自回归模型算法[23]修复的深度图像作为基准图像。为了说明基准图像的可靠性,本文选用Middle-bury数据集[24]中的Art、Moebius和Reinbeer 3个场景进行实验,并分别人为添加空洞,使用自回归模型算法进行修复,其修复结果如图 7所示。由图 7可知,该算法修复后的图像与原始图像在图像质量上没有明显的差异。同时,引入结构相似性(Structural Similarity, SSIM)量化该算法的修复效果,经计算,3个场景的SSIM值分别为0.955、0.985、0.978,修复时间分别为41.44、41.38、40.33 s。由此可见,其量化结果虽与原始图像质量还存在一定的差距,且修复时间较长,均在40 s以上,但其修复后的图像与原始图像的结构相似性在95.5%以上,在一定程度上能够对不同算法的优劣进行量化比较。
 |
| 图 7 自回归模型算法修复结果 |
经与原始图像的PSNR值相比,实验采用的各种算法的PSNR值均有较大的提升。如图 8(a)所示,本文算法在3个场景下的PSNR值分别为34.2、28.6、34.4 dB,均优于对比的双边滤波算法、联合双边滤波算法和形态学滤波算法修复的值;同时,由图 8(b)也可得到,本文算法的RMSE值分别为5.0、9.5和4.8,均小于对比算法的值。本文算法的PNSR值相较于双边滤波算法、联合双边算法和形态学滤波算法分别平均提高了16.5%、17.9%和1.7%,RMSE值分别平均降低了42.8%、42.2%和5.6%。这说明,本文所提的融合光线追踪和中值滤波算法对深度图像空洞修复有较强的鲁棒性。
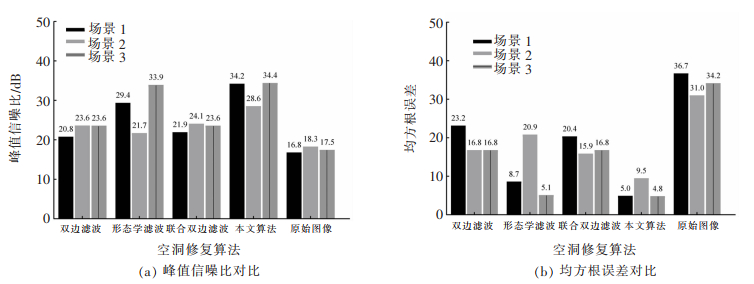 |
| 图 8 4种算法量化指标对比 |
针对深度图像在采集过程存在空洞的问题,本文采用融合光线追踪和中值滤波算法对采集的深度图像进行空洞修复和平滑处理。与双边滤波算法、联合双边算法和形态学滤波算法修复结果相比,本文所提的算法能够较好地对深度图像空洞进行深度值相对准确的修复,并且本文算法在处理物体边缘和较大范围的空洞修复时,能够保持边缘纹理清晰。由于本文算法需要在多帧深度图像数据情况下进行空洞修复,因而,无法对单帧的深度图像进行空洞修复,今后的工作将主要面向于对单帧深度图像进行实时有效的空洞修复。
| [1] |
LIU H M, TANG X C, SHEN S H. Depth-map completion for large indoor scene reconstruction[J]. Pattern Recognition, 2020, 99: 107112. DOI:10.1016/j.patcog.2019.107112 |
| [2] |
费点, 陈建林, 刘东生, 等. 基于深度相机的特殊表面定位与修复[J]. 光学学报, 2020, 40(21): 122-131. |
| [3] |
赵会军, 谭瑞珍, 刘德儿. 用于盲人导航的GML空间数据建模方法研究[J]. 江西理工大学学报, 2018, 39(5): 52-57. |
| [4] |
王紫薇, 邓慧萍, 向森, 等. 基于CNN的彩色图像引导的深度图像超分辨率重建[J]. 图学学报, 2020, 41(2): 262-269. |
| [5] |
HU Y G, XIAO M Q, LI S Y, et al. Aerial infrared target tracking based on a Siamese network and traditional features[J]. Infrared Physics & Technology, 2020, 111: 103505. |
| [6] |
MARíN-JIMéNEZ M J, ROMERO-RAMIREZ F J, MUÑOZ-SALINAS R, et al. 3D human pose estimation from depth maps using a deep combination of poses[J]. Journal of Visual Communication and Image Representation, 2018, 55: 627-639. DOI:10.1016/j.jvcir.2018.07.010 |
| [7] |
邓佳丽. 基于多特征核相关滤波器的RGB-D目标跟踪[D]. 广州: 华南理工大学, 2018.
|
| [8] |
王亮, 翟志强, 朱忠祥, 等. 基于深度图像和神经网络的拖拉机识别与定位方法[J]. 农业机械学报, 2020(增刊2): 554-560. |
| [9] |
刘德儿, 唐武, 陈增辉, 等. 改进的SSD算法用于盲人户外出行多尺度障碍检测[J]. 江西理工大学学报, 2021, 42(1): 87-97. |
| [10] |
SCHWARZ M, MILAN A, PERIYASAMY A S, et al. RGB-D object detection and semantic segmentation for autonomous manipulation in clutter[J]. The International Journal of Robotics Research, 2018, 37(4/5): 437-51. |
| [11] |
CAMPLANI M, SALGADO L. Efficient spatio-temporal hole filling strategy for Kinect depth maps[J]. Three-Dimensional Image Processing (3DIP) and Applications Ⅱ, 2012, 8090(82900E): 1-10. |
| [12] |
LE A V, JUNG S W, WON C S. Directional joint bilateral filter for depth images[J]. Sensors (Basel, Switzerland), 2014, 14(7): 11362-11378. DOI:10.3390/s140711362 |
| [13] |
王得成, 陈向宁, 易辉, 等. 基于自适应联合双边滤波的深度图像空洞填充与优化算法[J]. 中国激光, 2019, 46(10): 294-301. |
| [14] |
胡天佑, 彭宗举, 焦任直, 等. 基于超像素分割的深度图像修复算法[J]. 光电子·激光, 2016, 27(10): 1120-1128. |
| [15] |
王殿伟, 陈鹏, 李大湘, 等. 基于深度融合的深度图像修复算法[J]. 光电子·激光, 2019, 30(6): 640-646. |
| [16] |
LI J W, GAO W, WU Y H. High-quality 3D reconstruction with depth super-resolution and completion[J]. IEEE Access, 2019, 7: 19370-19381. DOI:10.1109/ACCESS.2019.2895653 |
| [17] |
ZHANG Y D, FUNKHOUSER T. Deep depth completion of a single RGB-D image[C]//Proceeding of Conference on Computer Vision and Pattern Recognition, New York: IEEE, 2018: 175-185.
|
| [18] |
SCHIED C, KAPLANYAN A, WYMAN C, et al. Spatiotemporal variance-guided filtering: real-time reconstruction for path-traced global illumination[C]//Proceedings of High Performance Graphics, NewYork: ACM, 2017: 1-12.
|
| [19] |
漆建波, 谢东辉, 许月, 等. 三维辐射传输模型LESS原理及其应用[J]. 遥感技术与应用, 2019, 34(5): 914-924. |
| [20] |
KAPLANYAN A S, DACHSBACHER C. Path space regularization for holistic and robust light transport[J]. Computer Graphics Forum, 2013, 32. |
| [21] |
DAMMERTZ H, SEWTZ D, HANIKA J, et al. Edge-avoiding À-Trous wavelet transform for fast global illumination filtering[C]//Proceeding of the Conference on High Performance Graphic, Saarbrucken: ACM, 2010: 67-75.
|
| [22] |
MEINDS K, STOUT J, OVERVELD K V. Real-time temporal anti-aliasing for 3D graphics[C]//Proceeding of Vision, modeling and Visualizotibn conference Munchen: Aka GmbH, 2003: 337-344.
|
| [23] |
YANG J Y, YE X C, LI K, et al. Color-guided depth recovery from RGB-D data using an adaptive autoregressive model[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3443-3458. |
| [24] |
SCHARSTEIN D, PAL C. Learning conditional random fields for stereo[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE, 2007: 1-8.
|
 2022, Vol. 42
2022, Vol. 42

