| 基于IGWO-SVM模型的边坡安全系数估算 |
随着我国经济的不断发展,边坡工程的数量与种类越来越多。然而边坡失稳造成的滑坡灾害也时有发生,它不仅造成巨大的经济损失,甚至威胁人民群众的生命安全。因此,边坡安全问题已成为众多学者研究的重点课题,其中,安全系数的估算是关键。董建军等利用SBAS-InSAR监测高海拔排土场边坡安全稳定性[1];武梦婷等基于机器学习融合主成分分析法(PCA)、参数调整、影响因素权重分析等建立了一种边坡安全稳定性评价体系[2];徐宏等基于正交试验设计,运用MIDAS GTS NX有限元软件计算不同试验水平组合的边坡安全系数,对边坡安全系数影响因素的敏感性进行研究[3]。
影响边坡安全系数的因素有很多,主要包含边坡高度和坡角、容重、黏聚力、摩擦角和孔隙压力比等,边坡安全系数与这些因素存在非常复杂的非线性关系[4]。边坡稳定性预测通常使用极限平衡法、数值分析法和有限元法等确定性分析及不确定性分析。饶平平等利用极限分析法和强度折减法建立二维含水边坡,为水位下降过程中其边坡稳定性评估和设计施工提供指导[5];江胜华等通过变步长的折减方法,根据位移变化率—强度折减系数曲线的转折突变,判断边坡稳定的安全度[6]。这些确定性分析虽具精确度较高,但都存在一定的局限性,如计算受特定条件限制、计算量大等。近年来,随着计算机和机器学习使用的快速发展,神经网络和支持向量机等为边坡安全系数估算提供了一种新思路。人工免疫算法、遗传算法(GP)、BP神经网络算法和支持向量机(SVM)等[7-10]都陆续被应用于边坡安全系数估算,并取得了较好的效果。但上述估算模型也存在不足之处,如遗传算法收敛速度较慢,容易早熟;而BP神经网络算法泛化能力较弱,容易陷入局部最小,且需要较大的训练样本集[11]。支持向量机以统计学习理论为基础,以结构风险最小化为准则,不仅能很好地解决非线性和高维度问题,而且也适用于小样本的估算[12]。然而,支持向量机估算系数的精度在很大程度上由模型参数(惩罚系数(C)和核函数参数(g))决定,因此,需要结合智能优化算法来确定支持向量机模型参数的最优值。灰狼优化算法(GWO)是Mirjalili等[13]提出的一种新型智能优化算法,算法结构简单且容易实现,同时,也具有较好的寻优精度和收敛速度[14]。GWO算法中,收敛因子(a)随着迭代次数的增加呈线性递减,寻优过程曲线非线性且复杂,将导致寻优结果陷入局部最优,进而影响支持向量机估算系数的精度。
综上,本研究采用指数函数代替线性函数对收敛因子(a)进行递减,以改进灰狼优化算法,提高算法的全局寻优能力,并将改进的灰狼优化算法(IGWO)应用于支持向量机参数寻优,建立IGWO-SVM模型,从而实现对边坡安全系数的估算。
1 IGWO-SVM算法原理 1.1 IGWO原理GWO算法是根据灰狼捕食猎物活动而开发的一种智能优化算法,狼群内部有严格的等级制度,由高到低依次为α、β、δ、ω4个等级。在实际建模时,将适应度最好的3只狼视为α、β和δ,剩余的狼定义为ω,围绕着α、β和δ更新位置。
狼群围攻猎物的过程定义如式(1)所列。
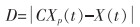
|
(1) |
式(1)中:D为灰狼与猎物间的距离;Xp(t)为猎物的位置;X(t)为各灰狼当前位置;C为系数。
各灰狼的位置更新公式定义如式(2)所列。
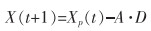
|
(2) |
式(2)中:X(t+1)为下一次迭代时的位置;A为系数。
系数A的计算公式定义如式(3)所列。
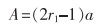
|
(3) |
式(3)中:α为收敛因子,r1为[0, 1]范围内的随机数。
系数C的计算公式定义如式(4)所列。
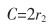
|
(4) |
式(4)中:r2为[0, 1]范围内的随机数。
在实际优化过程中,猎物的位置为未知数,只能假设α、β和δ狼知道猎物的潜在位置,使其他灰狼能进行位置更新。各灰狼围捕猎物的数学模型描述如式(5)所列。
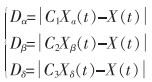
|
(5) |
式(5)中:Dα、Dβ、Dδ分别代表α、β、δ狼与其他灰狼的距离;Xα(t)、Xβ(t)、Xδ(t)分别代表α、β、δ狼当前的位置;C1、C2、C3为系数。
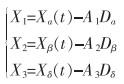
|
(6) |
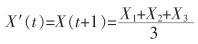
|
(7) |
式(6)、式(7)中:X′(t)为ω狼的当前位置,由式(6)和式(7)可知,ω狼的最终更新位置由α、β、δ狼共同决定。
在标准的GWO算法中,收敛因子(a)曲线是线性的。随着迭代次数由2递减到0,寻优过程为复杂的非线性曲线,这将导致寻优结果陷入局部最优。因此,本研究引入指数函数代替线性函数,使算法具有更好的全局寻优能力,指数函数公式如式(8)所列。
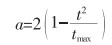
|
(8) |
式(8)中:t为当前迭代次数;tmax为最大迭代次数。
两个函数递减曲线如图 1所示,最大迭代次数为100次。
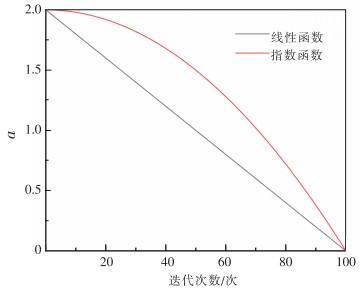 |
| 图 1 指数函数递减曲线 |
由图 1可知,指数函数的值高于线性函数,且大于1的情况占70%。当指数函数值高于线性函数的50%,说明算法具有更高的全局寻优能力,能更好地平衡算法全局寻优和局部寻优能力。
1.2 SVM原理SVM是解决分类和回归问题的一种常用方法,对非线性、高维度和小样本等问题依然适用。假设训练数据为(xi,yi),i=1,2,…,n(n为训练样本数量),其训练目标函数为:
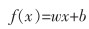
|
(9) |
式(9)中: w为权重向量;b为偏置常数。
根据结构风险最小化原则,回归问题可被转化为优化问题:
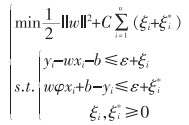
|
(10) |
式(10)中: C表示惩罚系数;ξi和ξi*为松弛因子;ε为训练时所允许的最大误差。
优化问题通过建立拉格朗日方程,得到的对偶表达式如下:
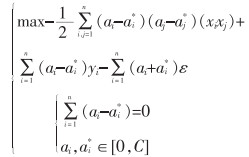
|
(11) |
式(11)中: ai和ai*为拉格朗日乘子,C为系数。
假设有边坡稳定实例数据样本,表示为(xi,yi),i=1,2,3,…,n,xi∈Rm,m为训练样本维数;n为训练样本个数,本研究选取6个衡量边坡稳定性状态(重度、黏聚力、摩擦角、坡角、高度和孔隙压力比)作为因子;yi为边坡稳定安全系数,可以建立关系式如式(12)所列。
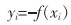
|
(12) |
通过二次规划算法进行求解,得到支持向量机边坡安全系数预测模型f(xi):
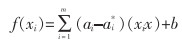
|
(13) |
将边坡数据输入SVM模型训练前,需先对数据进行归一化处理,以消除不同影响因素量纲的影响。将归一化后的数据作为SVM模型输入,训练时采用IGWO算法进行寻优,获取最优的惩罚系数(C)和核函数参数(g),建立IGWO-SVM模型。将模型应用于测试集,并通过平均绝对误差(MAE)、平均相对误差(MAPE)和均方根误差(RMSE)进行模型评价。IGWO-SVM模型流程如图 2所示。
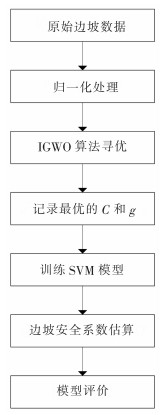 |
| 图 2 IGWO-SVM模型流程 |
本文选用文献[15]收集的82个典型边坡工程实例为研究对象,其中,将边坡安全系数的6个影响因素(重度、黏聚力、摩擦角、坡角、高度和孔隙压力比)作为模型输入,将安全系数作为模型输出。为与其他方法所得结果形成对比,将82个边坡样本中的前71个样本作为训练集,后11个样本作为测试集,如表 1所列。
|
|
表 1 训练集样本 |
在MATLAB软件中运行IGWO-SVM模型,为了验证IGWO-SVM的有效性,与GWO-SVM模型的估算结果作对比,2个模型的核函数均选取径向基核函数,边坡安全系数估算结果如表 2所列。其中,GWO算法寻优结果得到的惩罚系数(C)为1.155 3,核函数参数(g)为4.385 3,而IGWO算法的寻优结果显示得到的C为1.900 3,g为11.628 7,与GWO-SVM模型相比,IGWO-SVM模型的边坡安全系数估算结果与真实值更接近,说明IGWO的寻优结果更准确,也意味着指数函数代替线性函数对收敛因子(a)进行递减效果更佳,在一定程度上能提升寻优算法的全局寻优能力。
|
|
表 2 边坡安全系数预测结果比较 |
为更直观地展示模型估算的准确度,分别计算改进的BP模型、GP模型、GWO-SVM模型、IGWO-SVM模型预测结果的MAE、MAPE和RMSE值,并与文献[15-16]的估算结果进行对比。由表 2可知,IGWO-SVM模型的MAE、MAPE和RMSE值均为最小;与GWO-SVM模型相比,边坡安全系数估算精度较高。因此,IGWO-SVM模型估算边坡安全系数的精度比GWO-SVM模型更高,可精确预测边坡安全系数。
3 结论在原始灰狼优化算法的基础上,采用指数函数代替原始线性函数递减收敛因子(a),以建立改进的灰狼优化算法,并结合支持向量机构建了IGWO-SVM模型。结果表明,与传统GWO算法相比,IGWO算法的全局寻优能力更强。将模型应用于边坡安全系数估算,结果表明,IGWO-SVM模型的平均绝对误差(MAE)、平均相对误差(MAPE)、均方根误差(RMSE)均优于GWO-SVM模型,建立的IGWO-SVM模型估算边坡安全系数精度更高。因此,IGWO-SVM模型在工程应用中有一定的参考价值。
| [1] |
董建军, 梅媛, 李昕, 等. 高海拔排土场边坡安全稳定性SBAS-InSAR监测[J]. 中国安全科学学报, 2022, 32(1): 92-101. |
| [2] |
武梦婷, 陈秋松, 齐冲冲. 基于机器学习的边坡安全稳定性评价及防护措施[J]. 工程科学学报, 2022, 44(2): 180-188. |
| [3] |
徐宏, 夏琼, 王旭. 边坡安全系数影响因素敏感性分析[J]. 铁道建筑, 2021, 61(8): 98-101. |
| [4] |
王江荣, 袁维红, 任泰明, 等. 石头坪黄土高边坡稳定性的可靠度及敏感性分析[J]. 矿山测量, 2018, 46(5): 72-77. |
| [5] |
舒佳军, 李小双, 邓正定, 等. 极限平衡理论下寒区危岩稳定性及关键参数研究现状[J]. 有色金属科学与工程, 2022, 13(4): 91-97. |
| [6] |
江胜华, 汪时机, 李伟清, 等. 基于位移变化率和强度折减有限元的边坡失稳判定方法[J]. 农业工程学报, 2017, 33(15): 155-161. |
| [7] |
高文华, 罗新辉, 胡泽涛. 基于PCA-BP融合的边坡稳定性评价模型[J]. 安全与环境学报, 2016, 16(2): 6-10. |
| [8] |
乔金丽, 刘波, 李艳艳, 等. 基于遗传规划的边坡稳定安全系数预测[J]. 煤炭学报, 2010, 35(9): 1466-1469. |
| [9] |
张豪, 罗亦泳. 基于人工免疫算法的边坡稳定性预测模型[J]. 煤炭学报, 2012, 37(6): 911-917. |
| [10] |
王芬, 刘阳, 郝建斌, 等. 基于MABC-SVR的边坡安全系数预测模型[J]. 安全与环境工程, 2019, 26(2): 178-182. |
| [11] |
马春辉, 杨杰, 程琳, 等. 基于混合核函数HS-RVM的边坡稳定性分析[J]. 岩石力学与工程学报, 2017, 36(增刊1): 3409-3415. |
| [12] |
VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer, 1995: 156-160.
|
| [13] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. |
| [14] |
张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38. |
| [15] |
冯夏庭. 智能岩石力学导论[M]. 北京: 科学出版社, 2000.
|
| [16] |
苏国韶. 圆弧破坏型岩质边坡安全系数快速估计的高斯过程模型[J]. 应用基础与工程科学学报, 2010, 18(6): 959-966. |
 2022, Vol. 42
2022, Vol. 42