全球导航卫星系统(Global Navigation Satellite System, GNSS)能够为用户提供高精度的全球定位、导航和授时服务,因而在军用和民用领域都得到了广泛的应用,是军事活动和社会发展中不可或缺的基础设施[1]。
卫星导航系统一般采用高轨卫星,卫星距离地面大约20000 km,导致地面接收机接收到的卫星信号的功率很小,约为-160 dBW[2]。较低的信噪比使得到达接收机的卫星信号容易受到诸多干扰,例如压制式干扰、欺骗式干扰[3]。相对于压制式干扰,欺骗式干扰不易被接收机用户察觉,因此具有更大的危害[4]。文献[5]指出,只要欺骗信号功率大于真实信号4 dB,一段时间之后,接收机就能够跟踪到欺骗信号。
随着导航技术的广泛应用,针对导航系统的欺骗手段层出不穷。Todd等对欺骗技术进行了分类。从欺骗信号发射角度而言,欺骗技术可分为单欺骗源发射技术和多欺骗源发射技术[6]。单欺骗源欺骗技术利用单个信号发射源进行欺骗信号的发射,该欺骗源可以发射针对不同卫星的欺骗信号;多欺骗源发射技术利用多个欺骗源进行发射,每个欺骗源一般只发射针对某一颗卫星的欺骗信号,不同欺骗源发射的卫星欺骗信号一般不同。
近年来,国内外的专家学者对卫星导航信号欺骗检测技术进行了大量的研究,检测方法主要分为两类。一是基于信号特性的欺骗检测技术。例如Kim等[7]提出的基于信号到达时间的欺骗检测方法,Bitner等[8]提出的基于信号到达角的欺骗检测方法,Dehghanian等[9]提出的基于C/N0检测方法的监测技术,针对特定的环境都有一定的作用。第二类是基于外部辅助的欺骗检测技术。例如,Carson等[10]提出了一种雷达辅助的欺骗检测方法。该类方法需要额外添加设备,对民用接收机而言费用较为昂贵。所以,现阶段欺骗检测方法主要集中在第一类。
在接收机的跟踪阶段,载波环和码环能够输出多普勒频率、鉴相误差、载波相位和码相位等值,能够根据码相关峰的大小测量功率,为欺骗检测提供了许多重要参数。因此第一类欺骗检测技术中的跟踪阶段的欺骗检测方法研究成为导航抗欺骗领域的一个重要课题。例如,Psiaki等[11]针对单欺骗源发射的欺骗技术提出了双天线载波相位差值检测方法。该技术利用锁相环估计载波相位,当两个信号载波相位差小于设定的阈值时认为该组信号来自同一方向,此时判定为接收机受到欺骗;当来波方向各不相同时,判定未受到欺骗。该方法针对单欺骗源发射的欺骗信号有着良好的检测效果,但是当多个欺骗源发射欺骗信号时,该方法失效。Broumandan等[12]同样针对单欺骗源发射的欺骗技术提出基于信号空间关系的欺骗信号检测方法。该方法通过测量信号的多普勒频率来判定接收机是否受到欺骗。同一发射源发射的不同信号经过相同路径进入接收机,其幅度衰减以及多普勒变化规律是一致的。当测定的多普勒频率变化规律一致时,判定受到欺骗。该方法同样不适应于多欺骗源发射模式。赵陆文等[13]提出了一种基于载波跟踪谱分析的检测方法。该方法利用跟踪环路鉴相器输出信号的频谱特性与环路中是否存在干扰信号密切相关的特性,通过对鉴相器输出信号进行谱分析,建立欺骗检测模型,实现了欺骗信号检测。此方法能够较好地检测单欺骗源和多欺骗源发射的欺骗信号。
本文提出了一种基于跟踪环路统计特性分析的欺骗检测方法。该方法能够在单欺骗源和多欺骗源模式下,欺骗信号和真实信号频率不一致时检测出欺骗信号,并且检测性能相较于文献[13]得到了一定程度的提升。
1 系统模型无论欺骗者采取何种发射方式,接收机接收到的都是不同卫星发射的真实信号和欺骗源发射的欺骗信号叠加的复合信号。该复合信号通过接收机的捕获模块之后,与本地不同的伪随机码相关,依据码分多址的原理,解扩后的各个信号分别进入不同的接收机通道,进行跟踪以及后续解算。当针对某颗卫星的欺骗信号与该卫星发射的真实信号具有相同的伪随机码时,欺骗信号才会对真实信号的环路产生影响。因此在经过捕获模块之后,接收机每个通道跟踪到的实际上是某颗卫星真实信号和欺骗信号的叠加信号。因此,不管是单欺骗源还是多欺骗源发射,只需分析接收机跟踪的某个通道的信号即可代表其他接收通道的情况。
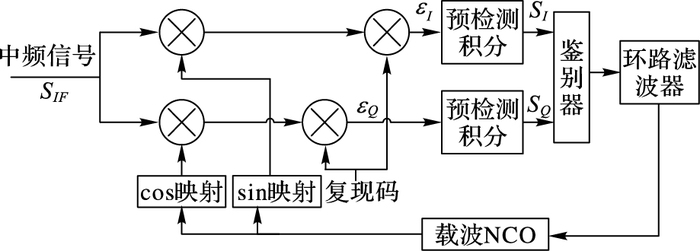
1.1 正常接收信号模型锁相环在导航接收机中用于载波跟踪。图 1为接收机中锁相环的结构图。首先,数字中频信号进入跟踪环路,分别与本地载波的同相和正交支路相乘,下变频到基带,得到两路信号(I路和Q路信号)。将得到的两路信号进行一定时长的预检测积分(通常为1 ms或者其整数倍),将积分后的数据进行鉴相,经环路滤波器后得到误差信号对本地复现的信号的参数进行修正。经过不断地迭代,最终接收机稳定的跟踪信号。
|
图 1 锁相环模型 Figure 1 Model of phase lock loop |
进入跟踪环路的中频信号为:
| ${S_{IF}}(t) = A(t)C(t)D(t){\rm{sin}}({\omega _{IF}}t + {\theta _{IF}}) + {n_{IF}}$ | (1) |
其中:A为信号幅度,C为伪随机码,D为数据,ωIF为中频频率,θIF为载波相位,nIF为均值为0、方差为σ2的高斯白噪声。
当本地码与伪随机码完全对齐时,解扩后的中频信号为:
| ${S_{IF}}(t) = A(t)D(t){\rm{sin}}({\omega _{IF}}t + {\theta _{IF}}) + {n_{IF}}$ | (2) |
nIF可用窄带随机过程表示为:
| ${n_{IF}} = {n_c}\left( t \right){\rm{cos}}\left( {{\omega _{IF}}t + {\theta _{IF}}} \right) + {n_s}\left( t \right){\rm{sin}}\left( {{\omega _{IF}}t + {\theta _{IF}}} \right)$ | (3) |
本地产生的两路正交的载波信号可表示为:
| ${S_{IL}} = {\rm{sin}}({\omega _L}t + {\theta _L})$ | (4) |
| ${S_{QL}} = {\rm{cos}}({\omega _L}t + {\theta _L})$ | (5) |
其中:SIL为同相信号,SQL为正交信号,ωL为本地载波频率,θL为本地载波相位。
将解扩后的中频信号与本地信号相乘,得到混频信号εI和εQ:
| $\begin{array}{l} {\varepsilon _I} = (A(t)D(t){\rm{cos}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 - \\ \quad \quad (A(t)D(t){\rm{cos}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 + \\ \quad \quad ({n_c}(t){\rm{sin}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 + \\ \quad \quad ({n_c}(t){\rm{sin}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 + \\ \quad \quad ({n_s}(t){\rm{cos}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 - \\ \quad \quad ({n_s}(t){\rm{cos}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 \end{array}$ | (6) |
| $\begin{array}{l} {\varepsilon _Q} = (A(t)D(t){\rm{sin}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 + \\ \quad \quad (A(t)D(t){\rm{sin}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 + \\ \quad \quad ({n_c}(t){\rm{cos}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 + \\ \quad \quad ({n_c}(t){\rm{cos}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 + \\ \quad \quad ({n_s}(t){\rm{sin}}(({\omega _{IF}} - {\omega _L})t + {\theta _{IF}} - {\theta _L}))/2 + \\ \quad \quad ({n_s}(t){\rm{sin}}(({\omega _{IF}} + {\omega _L})t + {\theta _{IF}} + {\theta _L}))/2 \end{array}$ | (7) |
对混频信号进行积分,积分时长设为T,假设在积分时间内幅度和数据均不变,则积分后的信号为:
| ${S_I}(t) = \frac{{ADT{\rm{cos}}(\varphi )}}{2} + \frac{{{N_C}{\rm{sin}}(\varphi )}}{2} + \frac{{{N_S}{\rm{cos}}(\varphi )}}{2}$ | (8) |
| ${S_Q}(t) = \frac{{ADT{\rm{sin}}(\varphi )}}{2} + \frac{{{N_C}{\rm{cos}}(\varphi )}}{2} + \frac{{{N_S}{\rm{sin}}(\varphi )}}{2}$ | (9) |
其中:φ=(ωIF-ωL) t+θIF-θL。NC与NS服从均值为零、方差为(σ2*T)/2的高斯分布。
当只存在真实信号时,锁相环能够稳定地跟踪该信号,鉴相误差φ趋向于0。因此,I路信号为积分后的数据和噪声,Q路信号则只有噪声。上面提到积分后的IQ支路噪声均服从均值为0、方差为(σ2*T)/2的高斯分布,而在积分时间内数据不会发生变化,因此I路信号服从均值为ADT/2、方差为(σ2*T)/2的高斯分布。I路与Q路标准差理论上相等。
1.2 欺骗信号入侵后的接收信号模型当欺骗信号进入时,此时跟踪环路跟踪到的是欺骗信号与真实信号的复合信号。以下是对复合信号的IQ路分布的分析。
欺骗信号可以表示为:
| ${S_S}(t) = {A_S}(t){C_S}(t){D_S}(t){\rm{sin}}({\omega _S}t + {\theta _S})$ | (10) |
其中:AS为欺骗信号幅度,CS为欺骗信号伪随机码,DS为欺骗信号数据,ωS为欺骗信号中频频率,θS为欺骗信号载波相位。
复合信号为两个信号的叠加:
| $\begin{array}{l} S(t) = A(t)C(t)D(t){\rm{sin}}({\omega _{IF}}t + {\theta _{IF}}) + \\ \quad \quad \quad {A_S}(t){C_S}(t){D_S}(t){\rm{sin}}({\omega _S}t + {\theta _S}) + n(t) \end{array}$ | (11) |
假设欺骗信号和真实信号码相位完全对齐,式(11) 可简化为:
| $\begin{array}{l} S(t) = C(t)D(t)(A(t){\rm{sin}}({\omega _{IF}}t + {\theta _{IF}}) + \\ \quad \quad {A_S}(t){\rm{sin}}({\omega _S}t + {\theta _S})) + n(t) \end{array}$ | (12) |
经过化简,得出式(13):
| $S(t) = C(t)D(t){A_M}(t){\rm{cos}}({\omega _{IF}}t + {\theta _M}) + n(t)$ | (13) |
其中:
假设AM(t)在积分时间内不变,则解扩、混频和积分之后的信号为:
| ${S_{IC}}(t) = \frac{{{A_M}(t)DT{\rm{cos}}({\varphi _M})}}{2} + \frac{{{N_C}{\rm{sin}}({\varphi _M}) + {N_S}{\rm{cos}}({\varphi _M})}}{2}$ | (14) |
| ${S_{QC}}(t) = \frac{{{A_M}(t)DT{\rm{sin}}({\varphi _M})}}{2} + \frac{{{N_C}{\rm{cos}}({\varphi _M}) + {N_S}{\rm{sin}}({\varphi _M})}}{2}$ | (15) |
其中:φM为复合信号与本地信号相位误差。
以上分析的都是理想情况,实际卫星信号的频率由于多普勒等因素的影响不是固定值,因此需要设置初始频偏以及频率变化率。为了不失一般性,假定频率变化率按照正弦规律变化[12]。
此时复合信号为:
| $\begin{array}{l} S(t) = A(t)C(t)D(t){\rm{sin}}({f_{ma}}{\rm{sin}}(\frac{{{f_{ma}}}}{{{f_{da}}}}{t^2}) + {\omega _{IF}}t + {\omega _{{\rm{int1}}}}t + \\ \quad \quad \quad {\theta _{IF}}) + {A_S}(t){C_S}(t){D_S}(t){\rm{sin}}({f_{ms}}{\rm{sin}}(\frac{{{f_{ms}}}}{{{f_{ds}}}}{t^2}) + \\ \quad \quad \quad {\omega _{IF}}t + {\omega _{{\mathop{\rm i}\nolimits} {\rm{nt}}2}}t + {\theta _S}) + n(t) \end{array}$ | (16) |
式(13) 中AM(t)和φM可以写为:
| $\begin{array}{l} {A_M}(t) = \\ \sqrt {{{(A(t))}^2} + {{({A_S}(t))}^2} + 2A(t){A_S}(t){\rm{cos}}(\Delta \omega t + \Delta {\omega _{{\rm{int}}}}t + \Delta f + \Delta \theta )} \\ {\theta _M} = {\rm{arcsin}}(\frac{{ - A(t){\rm{cos}}({\theta _{IF}} + {\omega _{{\mathop{\rm i}\nolimits} {\rm{nt}}1}}t + {f_{ma}}{\rm{sin}}(\frac{{{f_{ma}}}}{{{f_{da}}}}{t^2}))}}{{{A_M}(t)}} - \\ \quad \quad \quad \frac{{{A_S}(t){\rm{cos}}({\theta _S} + {\omega _{{\mathop{\rm int}} 2}}t + {f_{ms}}{\rm{sin}}(\frac{{{f_{ms}}}}{{{f_{ds}}}}{t^2}) + \Delta \omega t)}}{{{A_M}(t)}}) \end{array}$ |
其中:
由于锁相环能够跟踪信号并且实时估计出信号的频率与相位,因此φM趋向于0。由式(8) 和(9) 可知,在不存在欺骗信号时,由于卫星到达接收机的功率比较稳定,在一定时间内该支路的方差由噪声决定,所以I支路信号服从均值为ADT/2、方差为(σ2*T)/2的高斯分布;Q支路只有噪声,所以该支路服从均值为0、方差为(σ2*T)/2的高斯分布。加入欺骗信号之后,载波频率的细微差异会造成合成信号幅度AM(t)的振荡:当Δωt+Δωintt+Δf+Δθ为一常数时,AM(t)在较短时间内不会变化;当Δωt+Δωintt+Δf+Δθ波动时,I支路信号不服从均值为ADT/2、方差为(σ2*T)/2的高斯分布,而Q支路由于鉴相误差φM趋于零,幅度变化对该支路统计分布影响甚微,所以Q支路依然服从高斯分布。
根据上述分析,可以得出结论,欺骗信号的加入会导致跟踪环路中的I支路统计规律发生变化,进而导致I和Q支路积分值的分布统计值不相等。本文依据此原理鉴别接收机是否受到欺骗。
式(14) (15) 可以简化为:
| ${S_{IC}}(t) = \left( {{A_M}(t)DT + {N_S}} \right)/2$ | (17) |
| ${S_{QC}}(t) = {N_c}/2$ | (18) |
分别对式(17) 和(18) 的积分值求统计分布,统计一段时间内多个积分值的分布。如式(19) 和式(20) 所示:
| $I\_std = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({I_i} - {m_I})}^2}} } $ | (19) |
| $Q\_std = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({Q_i} - {m_Q})}^2}} } $ | (20) |
其中:Ii和Qi为I路和Q路积分值,N为该段时间内积分值个数,mI和mQ分别为I路与Q路积分值在该段时间内的平均值,然后进行式(19) 和式(20) 的计算,得到两路的分布统计值I_std和Q_std。利用式(21) 进行判决:
| $(\frac{{I\_std}}{{Q\_std}} > 1 - \gamma )\& (\frac{{I\_std}}{{Q\_std}} < 1 + \gamma )$ | (21) |
其中1-γ和1+γ为阈值。当式(21) 成立时,判定接收机未受到欺骗,反之则受到欺骗。
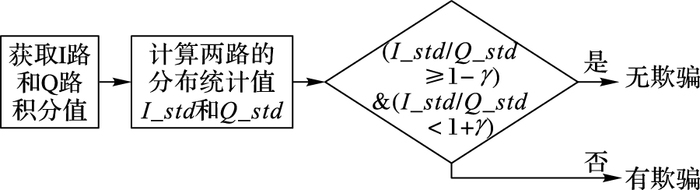
流程如图 2所示。
|
图 2 欺骗检测方法流程 Figure 2 Flow chart of spoofing detection method |
本次仿真使用已调制数据的锁相环,使用科斯塔斯环(Costas)中的atan鉴相方式。仿真环境为Matlab。由于由卫星带来的频率变化率不超过0.93 Hz/s,对于低动态用户,假设其频率变化率为2 Hz/s,则接收信号的载波频率相对于本振的变化率大致为3 Hz/s。
具体参数设置如表 1。
| 表 1 仿真参数设置 Table 1 Simulation parameter setting |
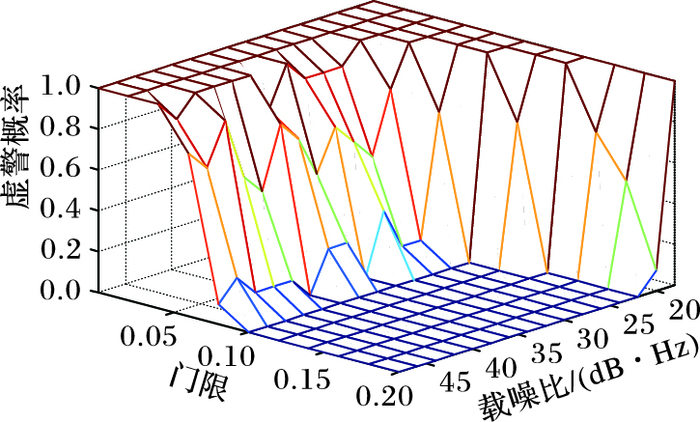
使用Matlab工具对所提方法进行仿真。由于式(8) 中的φ在0附近波动,所以I与Q路的积分值的标准差并不是严格意义上相等。文献[1]中指出,室外接收导航信号的载噪比一般为35 dB·Hz~55 dB·Hz,大于40 dB·Hz的视为强信号,小于28 dB·Hz的视为弱信号。根据实际情况,本文仿真载噪比范围确定为20 dB·Hz~60 dB·Hz。图 3为虚警概率与载噪比和门限的关系,载噪比在26 dB·Hz以上时,0.1~0.2的阈值虚警概率极小;经过实验数据分析,最终确定阈值为(1±0.1)。
|
图 3 虚警概率与载噪比和门限的关系 Figure 3 Relationship between false alarm probability and carrier-to-noise ratio and threshold |
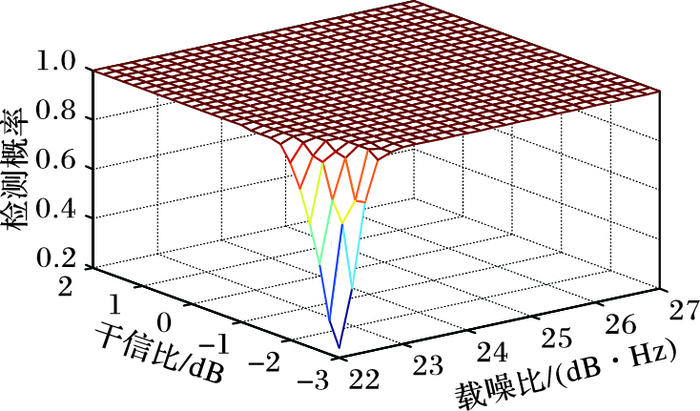
在信号载噪比处于正常情况时(28 dB·Hz~50 dB·Hz),固定载噪比,理论上检测概率随干信比的增大而增大。在欺骗信号与真实信号的干信比在接收机不易察觉的范围内(-10 dB~10 dB),固定干信比,理论上检测概率随载噪比的增加而增加。图 4为不同载噪比、不同干信比条件下的仿真结果。仿真条件设置为:载噪比在22 dB·Hz~30 dB·Hz,干信比在-3 dB~7 dB。进行1000次蒙特卡洛仿真。仿真结果表明,检测概率随信噪比和载噪比的增大而提高。
|
图 4 检测概率与载噪比和干信比的关系 Figure 4 Relationship between detection probability and carrier-to-noise ratio and interference to signal ratio |
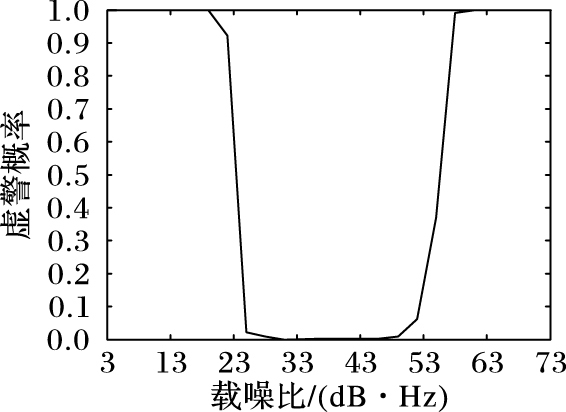
虚警概率指没有欺骗信号判定为存在欺骗信号。当不存在欺骗信号时,虚警概率在正常载噪比范围内(28 dB·Hz~50 dB·Hz)随载噪比的增大而减小。载噪比在28 dB·Hz以上时,在2%的虚警概率下能够获得100%的检测概率。仿真结果如图 5。仿真条件设置为:载噪比在3 dB·Hz~73 dB·Hz。进行1000次蒙特卡洛仿真。在载噪比超过正常接收范围并且继续增大时,虚警概率呈现上升的态势。过高的信噪比使噪声对I、Q支路的统计特性影响甚微,两支路将受到信号本身的波动的影响,不服从噪声的统计特性,从而增大虚警概率。
|
图 5 虚警概率随载噪比变化的趋势 Figure 5 Tend of false alarm probability varying with carrier-to-noise ratio |
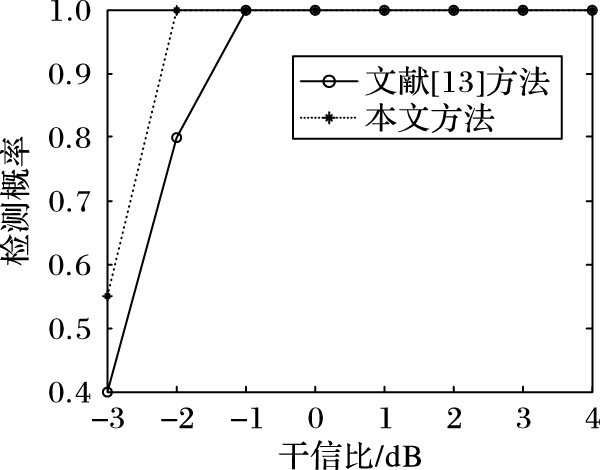
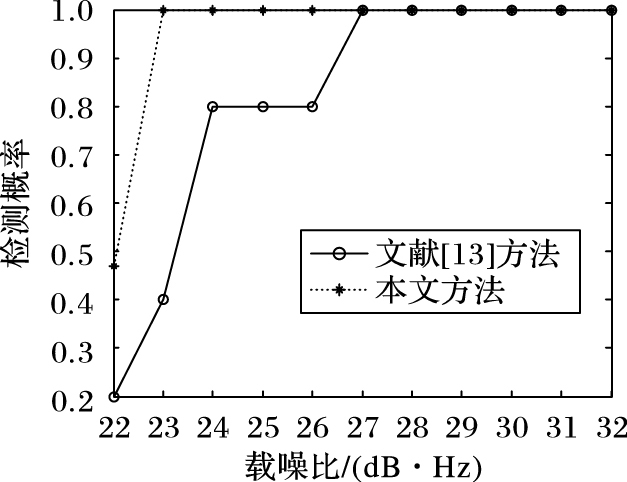
图 6和图 7为本文所提方法与文献[13]中方法的比较。结果表明,在固定载噪比(24 dB·Hz)的情况下,随着干信比的增大,检测概率增大,本文所提方法检测性能优于文献[13]所提方法;在固定干信比(-2 dB)的情况下,随着载噪比的增大,检测概率增大,本文所提方法的检测性能亦优于文献[13]方法。
|
图 6 两种方法的检测概率随干信比的变化 Figure 6 Detection probability of two methods change with interference-to-signal ratio |
|
图 7 两种方法的检测概率随载噪比的变化 Figure 7 Detection probability of two methods change with carrier-to-noise ratio |
本文通过研究载波跟踪环路I、Q路积分值的统计特性,提出一种基于跟踪环路统计特性分析的检测方法。该方法在室外正常接收载噪比范围内(28 dB·Hz~50 dB·Hz)可以有效地检测欺骗信号;并且与已有方法相比较,本文所提方法的检测性能有了一定程度的提升。
但是该方法也存在一定的不足。首先,文章只是在载波层面进行分析,假设码已经完全对齐,在实际接收机中码和载波是相互耦合的,码的对齐程度也在一定程度上会对信号的功率产生影响;其次,本方法适应于载波频率不同时的欺骗检测,当欺骗信号与真实信号同频同相时,无法检测是否存在欺骗;最后,该方法的提出建立在没有多径的基础上,现实环境中,多径会增大虚警概率。
| [1] | 相飞. 卫星导航接收机干扰及多径抑制方法研究[D]. 西安: 西安电子科技大学, 2013: 1-2. (XIANG F. Interference suppression and multipath mitigation methods for GNSS receivers[D]. Xi'an:Xidian University, 2013:1-2.) http://cdmd.cnki.com.cn/Article/CDMD-10701-1014324923.htm |
| [2] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 241-251. (XIE G. GPS Principle and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2009: 241-251.) |
| [3] | 胡源. 导航战中的GPS干扰研究[J]. 空间电子技术, 2009, 6(4): 48-52. (HU Y. Research of GPS jamming in navigation warfare[J]. Space Electronic Technology, 2009, 6(4): 48-52.) |
| [4] | LEDVINA B M, BENCZE W J, GALUSHA B, et al. An in-line anti-spoofing device for legacy civil GPS receivers[C]//Proceedings of the 2010 International Technical Meeting of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2010:698-712. |
| [5] | 黄龙, 吕志成, 王飞雪. 针对卫星导航接收机的欺骗干扰研究[J]. 宇航学报, 2012, 33(7): 884-890. (HUANG L, LYU Z C, WANG F X. Spoofing pattern research on GNSS receivers[J]. Journal of Astronautics, 2012, 33(7): 884-890.) |
| [6] | HUMPHREYS T E, LEDVINA B M, PSIAKI M L, et al. Assessing the spoofing threat:development of a portable GPS civilian spoofer[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2008:2314-2325. |
| [7] | KIM T H, SIN C S, LEE S. Analysis of effect of spoofing signal in GPS receiver[C]//Proceedings of the 201212th International Conference on Control, Automation and Systems. Piscataway, NJ:IEEE, 2012:2083-2087. |
| [8] | BITNER T, PRESTON S, BEVLY D. Multipath and spoofing detection using angle of arrival in a multi-antenna system[C]//Proceedings of the 2015 International Technical Meeting of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2015:822-832. |
| [9] | DEHGHANIAN V, NIELSEN J, LACHAPELLE G. GNSS spoofing detection based on receiver C/N0 estimates[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2012:2878-2884. |
| [10] | CARSON N, BEVLY D. A robust method for spoofing prevention and position recovery in attacks against networked GPS receivers[C]//Proceedings of the 2015 International Technical Meeting of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2015:623-632. |
| [11] | PSIAKI M L, O'HANLON B W, POWELL S P, et al. GNSS spoofing detection using two-antenna differential carrier phase[C]//Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation. Manassas, VA:The Institute of Navigation, 2014:2776-2800. |
| [12] | BROUMANDAN A, JAFARNIA-JAHROMI A, DEHGHANIAN V, et al. GNSS spoofing detection in handheld receivers based on signal spatial correlation[C]//Proceedings of the 2012 IEEE/ION Position Location and Navigation Symposium. Piscataway, NJ:IEEE, 2010:479-487. |
| [13] | 赵陆文, 缪志敏, 张北江, 等. 一种新的卫星导航跟踪段欺骗攻击检测方法[J]. 宇航学报, 2015, 36(10): 1172-1177. (ZHAO L W, MIAO Z M, ZHANG B J, et al. A novel spoofing attack detection method in satellite navigation tracking phase[J]. Journal of Astronautics, 2015, 36(10): 1172-1177. DOI:10.3873/j.issn.1000-1328.2015.10.011) |




