2. 北京遥感信息研究所, 北京 100011;
3. 苏州大学 城市轨道交通学院, 江苏 苏州 215137;
4. 中国科学技术大学 苏州研究院, 江苏 苏州 215123
2. Beijing Institute of Remote Sensing Information, Beijing 100011, China;
3. School of Urban Rail Transportation, Soochow University, Suzhou Jiangsu 215137, China;
4. Suzhou Institute for Advanced Study, University of Science and Technology of China, Suzhou Jiangsu 215123, China
近年来,众包(crowdsourcing)受到工业界和学术界的极大关注。在众包系统中,任务发布者并不是将任务分配给固定的员工完成,而是采用开放的方式将特定任务通过专门的发布平台(如Amazon Turk)分配给随机出现的工人完成。任务发布者通过众包系统可以充分利用互联网上的用户资源,发现新的创意或解决遇到的各类技术难题,以降低公司的运营成本或提高公司的创新能力。
目前,众包在很多领域已经得到了广泛的应用,并涌现出大量商用的众包平台。例如,利用众包平台对机器翻译的结果进行质量评估、识别海量图像进行分类以及评价网上商品的好坏等。然而,众包系统的发展也面临着挑战。由于众包系统中的任务完成者,也就是用户,是一个不确定的大众群体,使得用户完成任务的质量无法得到保证。部分自私的用户可能会为了自身利益,提交低质量甚至虚假的随机数据给平台。因此,为了保证众包系统的性能,必须设计出高效的任务分配机制,挑选出最合适的用户完成任务,从而保证任务的完成质量。
目前针对众包系统中的任务分配问题主要可以分为以下几类:文献[1]针对异质感知任务的成本问题,提出了一种动态招募用户的任务分配模型,并验证了所提出算法的高效性;文献[2]针对不同用户的任务选择情况,设计了一种分布式的感知任务分配模型;文献[3]考虑了移动群智感知中公平高效的任务分配,并解决了最小最大聚合感知时间问题;文献[4]提出了一种诚实的拍卖机制并致力于平台的效益最大化;文献[5]设计了一种基于中枢节点的多任务分发算法,实验结果证明该算法可以提高任务的完成速度。然而,上述研究都没有考虑用户的可靠性问题。不同的用户由于自身能力、对待任务的认真程度等因素的不同,完成任务的质量并不相同。也就是说,存在着用户可靠性的问题。平台在分配任务时应该尽可能地挑选高可靠性的用户完成任务。针对这一问题,目前对于众包中用户可靠性的研究主要有以下两个方面:1) 基于用户声誉机制的研究。把用户的信誉值看作是众包平台判别用户完成任务质量高低的重要指标,并且基于用户的可靠程度进行任务分配。比如在文献[6-7]提出了一种基于用户信誉值的激励机制,并通过仿真实验验证了激励机制的有效性。文献[8]针对众包系统中的激励和信誉机制的研究,设计了激励机制和信誉机制来确保用户尽最大努力的高质量的完成任务。文献[9]中Zhang等提出了基于用户信誉值的任务分配机制。文献[10]中He等提出了一种基于任务位置的最优任务分配算法,利用用户的信誉值和用户的位置进行任务分配。2) 激励机制设计。给予用户适当的奖励可以激发用户的工作潜力,进而保证了结果数据的质量。文献[11]提出了以平台为中心和以用户为中心的两种不同的感知系统模型并设计了与模型相适应的激励机制;文献[12]设计了一种离散的激励机制并实现了平台效益的最大化;文献[13]设计了一种基于反向拍卖的激励机制;文献[14]提出了一种基于最优的锦标赛模型,并设计了相应的激励机制;文献[15]结合反拍卖与Vickery拍卖思想,提出一种基于反拍卖模型的激励方法。上述研究均假设每个用户完成不同任务的可靠性都是相同的。然而这点在实际的众包系统中并不成立。由于用户所具备的技能不同,所以完成不同类型任务的可靠性应该也是不同的,因此还需要设计新的任务分配机制以解决该问题。
为了解决上述问题,本文假设每个用户针对不同类型的任务具有不同的用户可靠性,并以任务发布者的利益最大化为优化目标,设计了一种高效的基于用户可靠性的众包系统任务分配机制。首先,将所研究的任务分配问题抽象为一个整数规划问题;然后,采用贪心技术,实现了用户和任务之间的高效匹配。除此之外,还设计了一种用户可靠性的更新机制以及一种基于用户可靠性的报酬计算机制,以激励用户高质量地完成任务。最后,通过仿真实验对所设计机制的性能进行了验证。
1 问题模型本章将给出基于用户可靠性的众包任务分配模型,并对所研究的问题给出形式化的描述。
1.1 系统模型假设所研究的众包系统由一个任务发布者、一个众包任务分配平台和若干系统用户(即工人)组成。在每个任务分配周期,任务发布者首先在平台上发布n个任务,用集合T={t1, t2, …, tn}表示。由于所处的地理位置、要求的用户技能等因素的不同,所以集合T中的任务是异质的。对于每个任务ti∈T,可以用ti={Di, bi}来表示,其中Di是任务描述,包括ti的任务具体要求(如,技能要求等),而bi则表示任务ti报价,即任务发布者在用户完成任务后所愿意支付的最高报酬。用户在阅读完任务描述后,会将满足要求且感兴趣任务作为自身的任务请求发送给平台。假设系统中共有m个用户,且这些用户也是异质的。这些异质的用户由于所具备的技能、对待任务的认真程度等因素的不同,完成任务的质量是不同的。所以,对于用户集合W中的每个用户j∈W可以表示为j={Rj, Cj, Tj},其中Rj表示用户j的可靠性,每个ci, j∈Cj表示用户j高质量完成任务ti所需的成本,Tj是用户j提交给平台的感兴趣任务集合。由于每个用户完成不同任务的可靠性也可能不同,所以本文假设Rj是一个集合,每个ri, j∈Rj表示用户j完成任务ti的可靠性;ri, j反映了用户j以往完成与ti同类任务的情况,可靠性ri, j越高,说明用户j以往完成此类任务的质量越高。
平台在收到用户的任务请求之后,会根据一定的分配规则,完成用户与任务之间的匹配。为了保证任务的完成质量,本文假设每个任务可以同时分配给不超过l个用户去完成,而每个用户在每个任务分配阶段最多只会分配到一个任务。为了尽可能地保证每个任务都能够分配到用户并被高质量地完成,平台将会从任务的参与用户数和参与用户的可靠性两个方面来合理地选择用户并分配任务。最后,任务发布者在用户在完成任务后会根据任务的完成质量,计算每个用户应得的报酬。至此,一个任务分配周期结束。
1.2 问题描述本文要在考虑用户可靠性的基础上,设计一种众包系统任务分配机制,以任务发布者利益最大化为优化目标,实现用户与任务的最优匹配。
本文用yi, j={0, 1}表示任务ti是否可以被分配给用户j:若任务ti可以被分配给用户j,则yi, j=1,否则yi, j=0。同理,用xi, j={0, 1}表示任务ti是否分配给用户j:若ti分配给了用户j,则xi, j=1,否则xi, j=0。
每个用户完成任务后均会给任务发布者带来一定的收益。由于不同用户的可靠性不同,所以不同用户所能带来的利益也不同。假设用户高质量完成任务ti所能带来的利益为vi,那么用户j完成任务ti所能带来的利益可以用函数f(i, j)表示,且满足0≤f(i, j)≤vi。在本文中,取f(i, j)=ri, j vi,0≤ri, j≤1。用Wi表示所有分配给任务ti的用户集合,那么任务发布者从任务ti所能获得的收益为:
| $ {u_i} = \sum\limits_{j \in {W_i}} {{r_{i, j}}{v_i}-{p_{i, j}}} $ | (1) |
其中,pi, j为用户j完成任务ti后获得的报酬。为了激励用户更好地完成任务,所设计的机制在用户的任务完成质量和实际报酬之间建立关联,使得完成任务质量越高的用户,获得的报酬越多。因此,采用的具体报酬计算方式为:
| $ {p_{i, j}} = {r_{i, j}}{b_i} $ | (2) |
用户完成任务的质量越高,可靠性越高。从式(2) 不难看出,用户完成任务的质量越高得到的报酬也越高,可以激励用户认真完成任务。
综合式(1) 和(2),可以进一步得到:
| $ {u_i} = \sum\limits_{j \in {W_i}} {{r_{i, j}}\left( {{v_i} - {b_i}} \right)} $ | (3) |
本文的最终的优化目标是使任务发布者的收益最大化,可以规约为式(4) 所示的整数规划问题:
| $ \begin{array}{l} \max \sum\limits_{{t_i} \in T} {{u_i}} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\\ \left\{ \begin{array}{l} \sum\limits_{j \in W} {{x_{i, j}} \le l;\forall {t_i} \in T} \\ {x_{i, j}} = \left\{ {0, 1} \right\}, \forall {t_i} \in T;\forall j \in W\\ {u_i} = \sum\limits_{j \in W} {{r_{i, j}}\left( {{v_i}-{b_i}} \right){x_{i, j}}{y_{i, j}};\forall {t_i} \in T} \\ \sum\limits_{{t_i} \in T} {{x_{i, j}} \le 1;\forall j \in W} \end{array} \right. \end{array} $ | (4) |
其中:约束公式
本章将给出所设计机制的具体实现细节。所设计的机制主要包含两部分:基于用户可靠性的任务分配机制和用户可靠性的更新机制。
2.1 基于用户可靠性的任务分配机制为了解决式(4) 所示的整数规划问题,本文采用贪心技术,设计了一种基于用户可靠性的众包任务分配机制。在所设计的机制中,众包平台在收到所有用户的任务请求后,会以任务发布者的收益最大化为优化目标,实现用户和任务之间的匹配。所设计的任务分配机制如算法1所示。
算法1 基于用户可靠性的众包任务分配机制。
输入:用户集合W和任务集合T;
输出:任务分配结果X={xi, j}ti∈T, j∈W。
1) for{每个ti∈T}
2) {
3) for{每个用户j∈W}
4) {
5) 设置xi, j=0;
6) }
7) }
8) While (T≠Ø且W≠Ø)
9) {
10) 设置umax=0;
11) for{每个ti∈T}
12) {
13) for{每个用户j∈W}
14) {
15) if(ri, j(vi-bi)≥umax)
16) {
17) 设置umax=ri, jyi, j(vi-bi);
18) 设置tmax=i, wmax=j;
19) }
20) }
21) }
22) if(umax>0)
23) {
24) 设置xtmax, wmax=1;
25) 从集合W中删除用户j;
26) if(tmax已经分配给了l个用户)
27) 从集合T中删除任务tmax;
28) }
29) else
30) Return X;
31) }
32) Return X;
算法1的输入为初始的用户集合W和任务集合T,在平台将任务分配给用户后,将任务分配结果X={xi, j}ti∈T, j∈W作为输出返回给用户。
首先,算法1初始化任务分配结果中的所有变量xi, j=0。然后采用迭代的方式进行任务分配且每次迭代完成一个任务与用户之间的匹配。在每次迭代时,首先遍历所有的可行分配,找到一个能带来最大收益的分配方案。分别用tmax和wmax记录下能带来最大收益分配方案的任务和用户,并用umax表示该方案所能带来的收益。umax初始化为0。然后,判断任务发布者的收益是否还能继续提升,即判断umax是否大于0。若umax>0,则通过设置xtmax, wmax=1将任务tmax分配给用户wmax,并从集合W中删除用户j。除此之外,如果判断任务tmax已经分配给了l个用户,还需要将tmax从集合T中删除;否则,umax=0则表示任务发布者的收益无法继续提升,直接返回分配结果。除此之外,若在迭代过程中发现用户集合W或任务集合T为Ø,则表示任务分配已经结束,直接返回分配结果即可。
2.2 用户可靠性的更新机制在基于用户可靠性的众包系统分配机制中,本文需要用到用户的可靠性信息来计算任务分配所能带来的收益以及最终给用户的报酬。为了能使用户的可靠性信息能真实地反映用户近期完成任务的质量,每次任务分配结束后还应该根据本轮用户的任务完成质量更新该用户的可靠性信息。
用户完成任务后,众包平台可以根据一些已有的评价机制,例如多数表决(majority voting)机制对用户的任务完成质量进行评价。假设在第k轮的任务分配中,平台将任务ti分配给了用户j。平台对用户j最终完成任务的质量评价为ei, j(0≤ei, j≤1)。ei, j的值越大,说明用户j完成任务ti的质量越高,反之说明用户j完成任务的质量越低。由于用户完成不同类型任务的可靠性是不同的,所以可以对任务进行分类。用rjf表示用户j完成任务类型为f的用户可靠性。仍假设平台将任务ti分配给了用户j且任务ti的类型为f;那么,每轮任务分配结束后,平台计算得到的新的用户可靠性为:
| $ r_{k, j}^f = \alpha r_{k - 1, j}^f + (1 - \alpha ){e_{i, j}} $ | (5) |
其中:α是一个[0, 1]的常数,rk, jf表示用户j在第k轮任务分配结束后计算得到的完成任务类型为f的用户可靠性。通过调整α的大小,可以改变历史任务完成信息对报酬以及分配机制的影响。根据式(5) 可知,如果用户想要分配到任务且获得较高的报酬,必须要持续高质量地完成任务才行,从而达到激励用户认真完成任务的目的。
用户可靠性更新完成后,下一轮众包任务分配开始,更新后的用户可靠性信息将被用于在下一轮任务分配中计算收益以及报酬。
3 仿真实验本文提出了一种基于用户可靠性的众包任务分配机制,综合考虑用户完成任务的历史情况,采用了贪心的思想,实现了用户和任务之间的高效匹配。为验证本文提出机制的有效性,下面将给出所设计算法的仿真实验结果,并以此来分析和验证其实际性能。
接下来介绍一下评价算法好坏的相关指标:任务发布者的总收益和任务成交率。任务发布者的总收益定义为平台上所有发布任务的收益总和。任务成交率定义为平台上分配到用户的任务数量和平台上所有任务总数的比值。
在仿真实验中,只有一个任务发布者,平台上每个任务的报价为b∈[3, 6],每个任务最多分配给l=4个用户去完成。每个用户的初始可靠性r=0.5,每个用户完成任务的成本为c∈[1, 4],α=0.8。本文提出的任务分配算法是和文献[4]中的ProMoT(Profit Maximizing Truthful auction mechanism)进行对比实验的。
3.1 用户人数对任务发布者总收益有的影响仿真实验的第一部分主要分析用户人数与任务发布者的总收益之间的关系。在任务数n设置为60的情况下,对两种方法作对比实验,用户数m与任务发布者的总收益之间的关系如图 1所示。
|
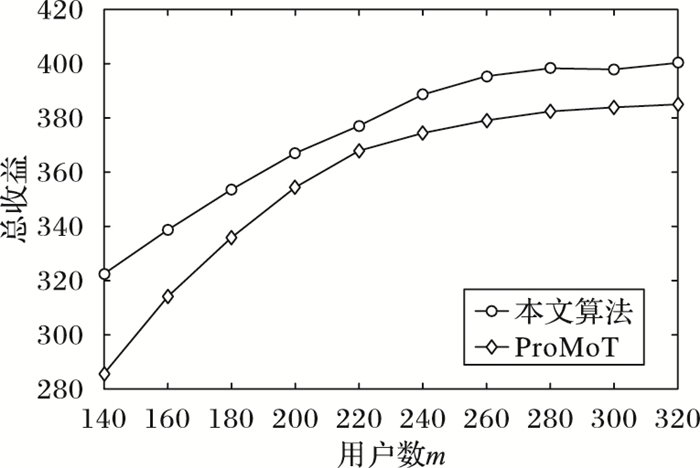
图 1 用户人数与任务发布者的总收益之间的关系(n=60) Figure 1 Relationship between number of users and total revenue of task publisher (n=60) |
由图 1可知,本文提出的任务分配算法优于ProMoT,可以使平台获得更多的收益,这是因为ProMoT在选择用户分配任务的时候没有考虑到用户的可靠性问题。在任务数量固定时,两条曲线的变化趋势大致相同,随着用户人数的增加,任务发布者的总收益也随之上升。刚开始,平台上用户人数较少,任务需求的用户数大于平台中用户总数。随着用户人数的增加,每个任务可以分配到的用户数也逐渐变多,被完成的任务数量也逐渐增多,那么任务发布者的总收益也随之上升。当用户人数超过一定数量后,每个任务都分配到了足够多的用户,任务发布者的总收益上升的速度变慢,最终任务发布者的总收益趋于平缓。
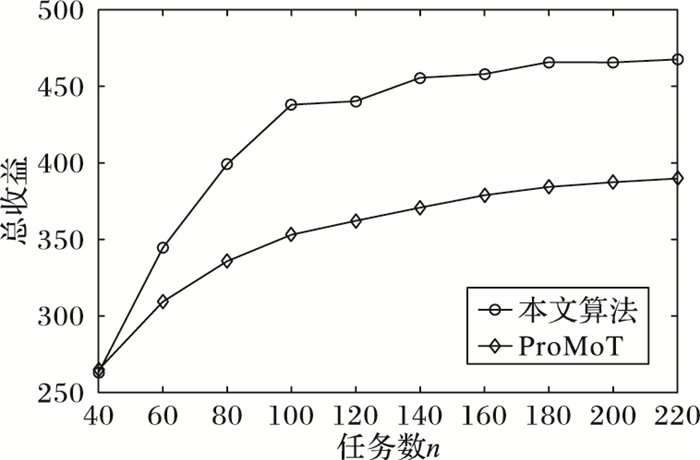
3.2 任务数量对任务发布者总收益的影响图 2给出了用户数量保持为200不变的条件下,任务数量与任务发布者总效益之间的关系。从实验结果可以看出,本文提出的基于用户可靠性的任务分配算法较之文献[4]中的ProMoT对平台收益提升帮助更大。这是因为ProMoT仅仅考虑了当前用户报价的高低,忽略了用户在完成任务时的可靠性问题。在用户数量一定的情况下,随着平台上发布任务数量的增加,任务发布者的总收益也随之上升。但是,当平台上发布任务数量超过一定数量后,任务所需求的用户数量超过了平台上的用户数量,任务发布者的总收益上升速度逐渐降低,最终趋于平稳。
|
图 2 任务数与任务发布者总收益之间的关系(m=200) Figure 2 Relationship between number of tasks andtotal revenue of task publisher (m=200) |
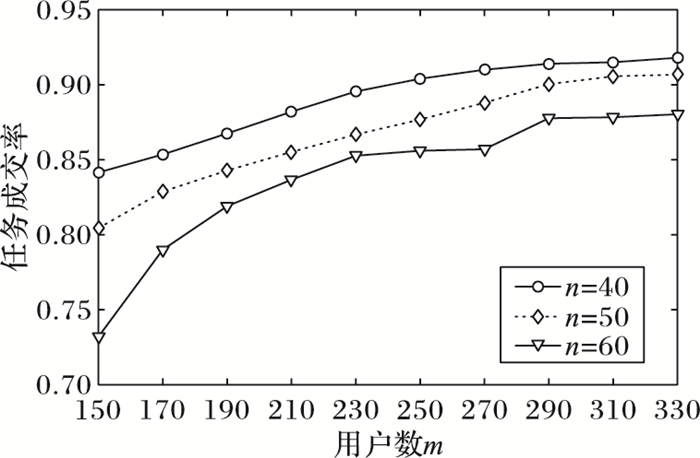
为了验证不同任务数量对任务成交率的影响,对任务数量进行实验对比,分别针对n=40,n=50和n=60进行实验验证,实验对比结果如图 3所示。从实验结果可以看出,当n=60时,平台上任务成交率最高。在任务数量固定的情况下,随着用户数量的增加,每个任务都能够分配到用户,任务成交率也在不断提高。当用户人数超过一定数量后,因为平台上符合任务要求的用户已经分配到任务,剩下的任务没有用户符合要求, 所以最终任务成交率会达到一个平稳的趋势。
|
图 3 用户人数与任务成交率之间的关系 Figure 3 Relationship between number of users and task turnover rate |
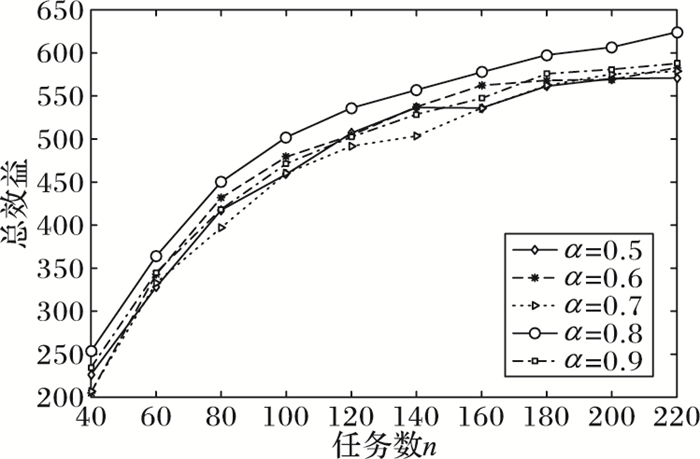
仿真实验的第四部分主要分析可靠性更新系数α与任务发布者总收益之间的关系。在系数α分别设置为0.5、0.6、0.7、0.8和0.9五种情况下,系数α与任务发布者总收益之间的关系如图 4所示。
|
图 4 可靠性更新系数α与任务发布者总收益之间的关系 Figure 4 Relationship between reliability updating coefficient α and total revenue of task publisher |
在该实验中没有选取更小的可靠性更新系数α,这是因为本文希望在用户的可靠性更新过程中,用户的历史可靠性占主要部分。从实验结果可以看出,随着系数α的增加,任务发布者总收益也呈现上升的趋势。当α=0.8时,任务发布者总收益达到最大;当α>0.8时,该可靠性更新方法就退化为传统的可靠性更新方法,所以为了提高整个众包平台中任务发布者的总效益,设定α=0.8。
4 结语本文针对众包系统中的任务分配机制进行了研究,主要解决了已有研究中存在的未充分考虑用户的可靠性问题,特别是用户针对不同类型的任务具有不同的可靠性的问题。研究首先以任务发布者的收益最大化为优化目标,采用贪心技术,设计了一种基于用户可靠性的任务分配机制。然后设计了一种用户可靠性的更新机制和报酬计算机制,以激励用户高质量地完成任务。最后,通过仿真实验证明了所设计任务分配机制的高效性。
| [1] | LI H, LI T, WANG Y. Dynamic participant recruitment of mobile crowd sensing for heterogeneous sensing tasks[C]//Proceedings of the 2015 IEEE 12th International Conference on Mobile Ad Hoc and Sensor Systems. Washington, DC:IEEE Computer Society, 2015:136-144. |
| [2] | CHEUNG M H, SOUTHWELL R, HOU F, et al. Distributed time-sensitive task selection in mobile crowdsensing[C]//Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing. New York:ACM, 2015:157-166. |
| [3] | ZHAO Q, ZHU Y, ZHU H, et al. Fair energy-efficient sensing task allocation in participatory sensing with smartphones[C]//Proceedings of the 2014 IEEE Conference on Computer Communications. Piscataway, NJ:IEEE, 2014:1366-1374. |
| [4] | SHAH-MANSOURI H, WONG V W S. Profit maximization in mobile crowdsourcing:a truthful auction mechanism[C]//Proceedings of the 2015 IEEE International Conference on Communications. Piscataway, NJ:IEEE, 2015:3216-3221. |
| [5] | 徐哲, 李卓, 陈昕. 面向移动群智感知的多任务分发算法[J]. 计算机应用, 2017, 37(1): 18-23. (XU Z, LI Z, CHEN X. Multi-task assignment algorithm for mobile crowdsensing[J]. Journal of Computer Applications, 2017, 37(1): 18-23. DOI:10.11772/j.issn.1001-9081.2017.01.0018) |
| [6] | 芮兰兰, 张攀, 黄豪球, 等. 一种面向众包的基于信誉值的激励机制[J]. 电子与信息学报, 2016, 38(7): 1808-1815. (RUI L L, ZHANG P, HUANG H Q, et al. Reputation-based incentive mechanisms in crowdsourcing[J]. Journal of Electronics & Information Technology, 2016, 38(7): 1808-1815.) |
| [7] | KATMADA A, SATSIOU A, KOMPATSIARIS I. A reputation-based incentive mechanism for a crowdsourcing platform for financial awareness[EB/OL].[2016-11-19]. http://projectprofit.eu/wp-content/uploads/2016/03/chp3A10.10072F978-3-319-50237-3_2.compressed.pdf. |
| [8] | 王莹洁, 蔡志鹏, 童向荣, 等. 基于声誉的移动众包系统的在线激励机制[J]. 计算机应用, 2016, 36(8): 2121-2127. (WANG Y J, CAI Z P, TONG X R, et al. Online incentive mechanism based on reputation for mobile crowdsourcing system[J]. Journal of Computer Applications, 2016, 36(8): 2121-2127. DOI:10.11772/j.issn.1001-9081.2016.08.2121) |
| [9] | ZHANG Y, VAN DER SCHAAR M. Reputation-based incentive protocols in crowdsourcing applications[C]//Proceedings of the 2012 IEEE INFOCOM. Piscataway, NJ:IEEE, 2012:2140-2148. |
| [10] | HE S, SHIN D H, ZHANG J, et al. Toward optimal allocation of location dependent tasks in crowdsensing[C]//Proceedings of the 2014 IEEE Conference on Computer Communications. Piscataway, NJ:IEEE, 2014:745-753. |
| [11] | YANG D, XUE G, FANG X, et al. Crowdsourcing to smartphones:incentive mechanism design for mobile phone sensing[C]//Proceedings of the 18th Annual International Conference on Mobile Computing and Networking. New York:ACM, 2012:173-184. |
| [12] | JI S, CHEN T. Crowdsensing incentive mechanisms for mobile systems with finite precisions[C]//Proceedings of the 2014 IEEE International Conference on Communications. Piscataway, NJ:IEEE, 2014:2544-2549. |
| [13] | ZHU X, AN J, YANG M, et al. A fair incentive mechanism for crowdsourcing in crowd sensing[J]. IEEE Internet of Things Journal, 2016, 3(6): 1364-1372. DOI:10.1109/JIOT.2016.2600634 |
| [14] | ZHANG Y, JIANG C, SONG L, et al. Incentive mechanism for mobile crowdsourcing using an optimized tournament model[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(4): 880-892. DOI:10.1109/JSAC.2017.2680798 |
| [15] | 朱旋, 杨麦顺, 安健, 等. 群智感知中基于反拍卖模型的众包激励方法[J]. 计算机应用, 2016, 36(7): 2038-2045. (ZHU X, YANG M S, AN J, et al. Crowdsourcing incentive method based on reverse auction model in crowd sensing[J]. Journal of Computer Applications, 2016, 36(7): 2038-2045. DOI:10.11772/j.issn.1001-9081.2016.07.2038) |




