2. 重庆城市综合交通枢纽开发投资有限公司, 重庆 401121
2. Chongqing Integrated Transport Hub Development Investment Company Limited, Chongqing 401121, China
目前,许多智能交通系统(Intelligent Transportation System,ITS)应用服务,如车辆导航、出行路线规划、交通流量管理、交通事故预警与处置、公交到站时间预测等都需要位置信息。近年来,随着智能终端技术发展与普及,各种车辆和移动终端已将全球定位系统(Global Positioning System, GPS)模块作为标配,GPS已成为ITS应用服务提供位置信息的主流定位技术。
尽管GPS技术已很成熟,但由于城市道路密集且形状复杂,在车辆经过多层立交桥、隧道或高层建筑时,GPS信号会丢失或变差。此外,电子地图中的道路也存在误差,定位数据并不能直接正确显示到电子地图中的道路上。地图匹配作为一种位置修正技术可以解决这个问题。
地图匹配算法是以定位系统(GPS或GPS/DR等)产生的轨迹数据以及高精度路网数据作为输入,以此来识别车辆正在行驶的正确路段并确定车辆在路段上的位置[1]。目前,实时地图匹配算法可以分为简单匹配算法、基于权重匹配算法和高级匹配算法三类[2]。简单匹配算法仅考虑了道路网的几何形状,算法简单但是在交叉路和平行路段匹配精度不高[3];基于权重匹配算法除了考虑道路网的几何形状外,还综合考虑了道路间的连接或连通关系,常基于几个度量指标如距离、方向等给每条候选路段打分,然后选择得分最高路段作为匹配路段[4-6];高级匹配算法会利用数学模型如隐马尔可夫模型(Hidden Markov Model,HMM)[7-9]、模糊逻辑[10-11]、D-S(Dempster-Shafer)证据理论[12]、卡尔曼滤波等来给候选路段计算分数,并选择得分最高路段作为匹配路段。尽管高级匹配算法匹配正确率一般比基于权重算法高,但是高级算法具有更高的复杂度,可能会产生较大的匹配延迟[2]。
目前基于权重匹配算法的准确率介于简单匹配算法和高级匹配算法之间,但其算法复杂性低,比较适合实时地图匹配。文献[4]就该类算法的权重系数为经验常数,不能适应匹配场景变化[2]的问题进行了改进:根据每个GPS轨迹点自身的水平精度、速度、与上一个GPS轨迹点的行驶距离,建立了三个权重系数函数,权重系数将随着GPS轨迹点动态变化,算法平均匹配正确率可达到92.19%。但是,该算法权重仅考虑了当前GPS轨迹点及候选路段的拓扑信息,没有考虑与历史匹配路段的时空关系,因此在GPS信号质量差时,可能会在平行路段及道路夹角很小路段出现误匹配。本文针对该类问题,考虑GPS轨迹的时空特性,提出了一种改进的基于动态权重的实时地图匹配算法。该算法主要特点表现在以下几方面:
1) 增加道路连通性权重,这可以解决跳段问题[2]和平行道路匹配问题;
2) 除距离权重外的其他三个权重都考虑了与历史匹配点和匹配路段的时空关系,可以解决包括Y形道路在内的多支路道路的匹配;
3) 权重系数随着GPS轨迹点动态变化,可以解决由于候选路段得分很相近导致的“过度拟合”型匹配错误。
1 地图匹配基本概念GPS轨迹T是由装有GPS模块的设备采集的,由一系列按时间先后顺序记录的GPS轨迹点组成的集合,表示为T={p1, p2, …, pn}。每个GPS轨迹点具有6个属性,表示为向量:
pi=[lon, lat, t, v, comp, hdop]
其中:pi.lon是经度,pi.lat是纬度,pi.t是记录时间戳,pi.v是瞬时速度,pi.comp是瞬时方向,pi.hdop是水平精度。
本文将路网当作一个有向图G,G中的顶点是路网的道路节点,具有经度、纬度属性。如图 1,路段r1是连接N1、N2两个道路节点的有向边,表示G中道路的中心线。路段r有5个属性,表示为向量:
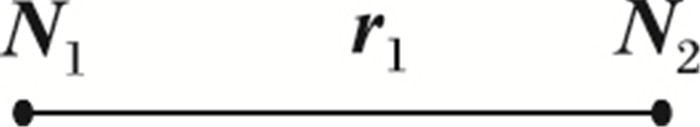
|
图 1 路段 Figure 1 Road segment |
r=[dir, len, type, start, end]
其中:r.dir是路段通行方向,r.len是路段长度,r.type是路段类型(国道、高速路等),r.start是路段点,r.end是路段终点。弯道由多条路段表示。
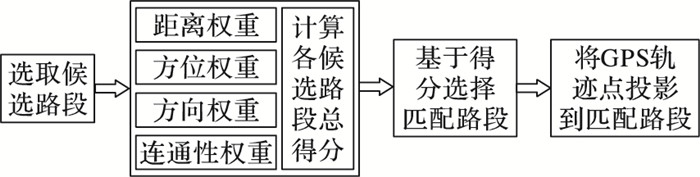
2 一种动态权重实时匹配算法算法的总体逻辑如图 2。
|
图 2 算法总体逻辑框图 Figure 2 Overview of algorithm framework |
地图匹配算法实质是从整个路网(解空间)寻找最优路径的一种搜索算法。寻找候选路段过程就是对解空间剪枝,简单快速的候选路段选取方法能大大提高算法的匹配效率。目前已有的方案有误差椭圆法和网格搜索法:误差椭圆法[10, 13]数学理论复杂,而且实现比较复杂,对算法效率可能影响较大;网格搜索法[14-15]的搜索效率非常高,但是对地图数据建立网格索引是一个较复杂的过程。
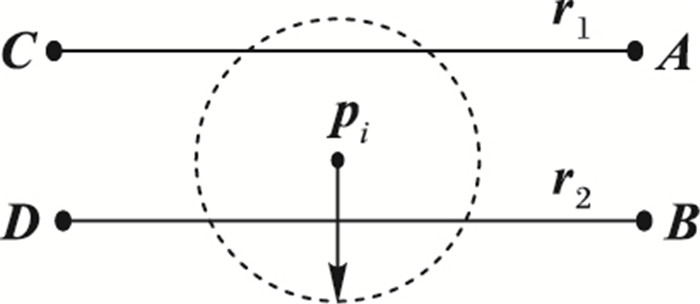
为了简单但又不失效率和准确性,本文采用误差圆法。如图 3,以GPS轨迹点pi为圆心,其精度R为半径得到误差圆,任何被误差圆包含的路段和与误差圆所在区域相交或相切的路段都将被选作pi的候选路段:
|
图 3 基于误差圆选取候选路段 Figure 3 Candidate road segments selection based on error circle |
Ci={ri1, ri2, …, rik}
这解决了基于道路节点的误差圆法可能找不到候选路段的问题。
2.2 计算各候选路段的总得分本文基于四个指标,即距离权重、方位权重、方向权重和连通性权重,对每条候选路段打分。具体细节将在稍后各小节详述。
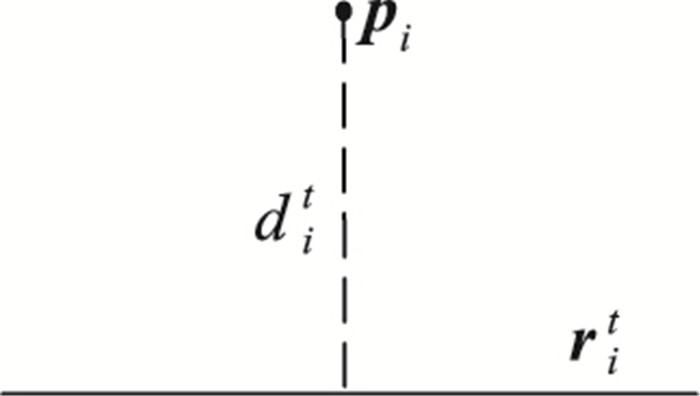
2.2.1 距离权重距离权重是利用GPS轨迹点pi到它候选路段rit的垂直投影距离得到的。如图 4,距离dit越小,pi匹配到这条候选路段的可能性越大。
|
图 4 GPS轨迹点到候选路段距离 Figure 4 Perpendicular projection distance to candidate road segment of GPS points |
对样本轨迹数据进行分析发现,GPS轨迹点到候选路段的距离服从高斯分布,该结论在文献[8]中也有提及。为简化模型,假设距离期望为0,均方差为σg, 那么pi匹配到候选路段rit的概率为:
| $ P_{_i}^{^t} = \frac{1}{{\sqrt {2\pi } {\sigma _g}}}{{\rm{e}}^{-{{{\rm{(}}d_{_i}^{^t}{\rm{)}}}^2}{\rm{/ }}2\sigma _{_g}^{^2}}} $ | (1) |
将其值归一化到, 得到距离权重计算公式:
| $ Dist_{_i}^{^t} = {{\rm{e}}^{-{\rm{ }}{{(d_{_i}^{^t})}^2}/2\sigma _{_g}^{^2}}} $ | (2) |
其中:dit是pi到它第t条候选路段rit的垂直投影距离;σg通过MAD法(Median Absolute Deviation)求得,即
| $ {\sigma _g} = 1.4826 \times \mathop {{\rm{median}}}\limits_i \left( {\left| {{d_i}-\mathop {{\rm{median}}}\limits_j \left( {{d_j}} \right)} \right|} \right) $ | (3) |
利用5 700个GPS轨迹点计算出σg=17.15。
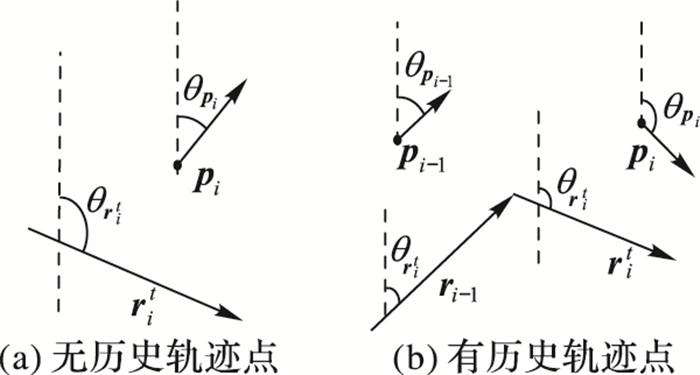
2.2.2 方位权重如图 5,以正北方向为基准方向,θpi是GPS轨迹点pi的方位角,θrit是候选路段rit的通行方向角。则道路rit与pi的方向夹角为θit:
|
图 5 计算方位权重的两种情况 Figure 5 Two cases of heading weight calculation |
| $ \theta _i^t = \left\{ \begin{array}{l} |{\theta _{\mathit{\boldsymbol{r}}_i^t}}-{\theta _{{\mathit{\boldsymbol{p}}_i}}}|, \;\;\;\;\;\;\;\;\;\;\;\;|{\theta _{\mathit{\boldsymbol{r}}_i^t}}-{\theta _{{\mathit{\boldsymbol{p}}_i}}}| \le 180^\circ \\ 360^\circ-|{\theta _{\mathit{\boldsymbol{r}}_i^t}} - {\theta _{{\mathit{\boldsymbol{p}}_i}}}|, \;\;|{\theta _{\mathit{\boldsymbol{r}}_i^t}} - {\theta _{{\mathit{\boldsymbol{p}}_i}}}| > 180^\circ \end{array} \right. $ | (4) |
θit越小,pi匹配到rit的可能性越大。当pi无历史轨迹点时,如图 5(a),本文用式(5) 计算方位权重:
| $ Hea{d_i}^t = \left( {1 + {\rm{cos}}\theta _i^t} \right)/2 $ | (5) |
当车辆转弯时,GPS轨迹点瞬时方向随着道路方向变化而变化,因此当pi有历史匹配信息时,如图 5(b),结合历史轨迹点和历史匹配路段的方向信息描述该变化趋势,用式(6) 计算方位权重,降低方位权重对方向误差的敏感度:
| $ Head_{_i}^{^t} = \left( {1 + {\rm{cos}}\left| {{\theta _{\mathit{\boldsymbol{r}}_{i-1 \to i}^t}}{\rm{ }}-{\rm{ }}{\theta _{_{i-1 \to i}}}} \right|} \right)/2 $ | (6) |
其中:θri-1→it是当前候选路段rit与历史匹配路段ri-1通行方向的夹角,θi-1→i是pi与pi-1瞬时方向的夹角。
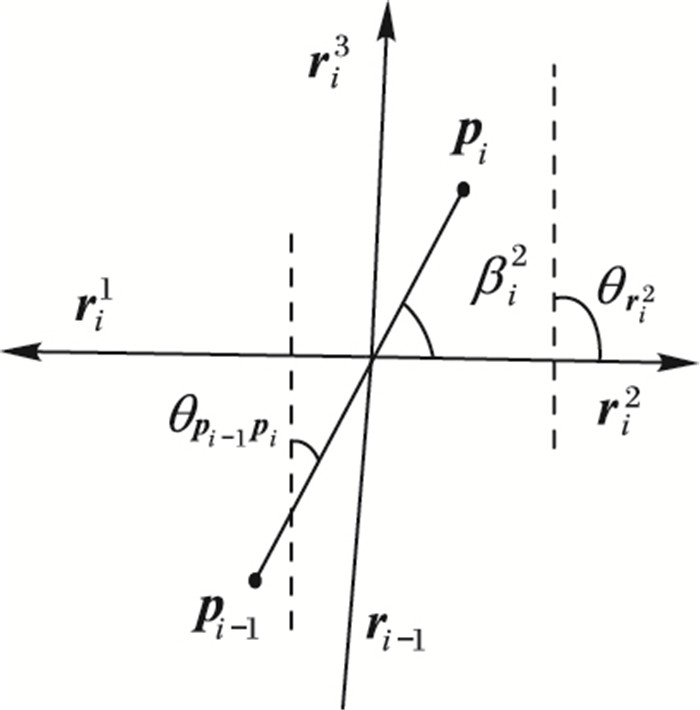
2.2.3 方向权重在车辆通过路口时,GPS轨迹点瞬时方向的误差由于车辆速度低而变大,导致方位权重的误差变大。为了提高车辆经过路口时的正确匹配率,利用了GPS轨迹点pi与历史GPS轨迹点pi-1的连线方向θpi-1pi和pi候选路段rit方向θrit的关系来确定匹配路段,pi-1pi与rit的夹角βit越小,表明pi匹配到候选路段rit的可能性越大,方向权重也越大。如图 6,pi-1匹配到路段ri-1, pi的候选路段为ri1、ri2、ri3, pi-1pi与候选路段ri2的夹角βi2越小,pi匹配到ri2的可能性越高。
|
图 6 方向权重 Figure 6 Direction weight |
| $ \beta _i^t = \left\{ \begin{array}{l} \left| {{\theta _{\mathit{\boldsymbol{r}}_i^t}}-{\theta _{{\mathit{\boldsymbol{p}}_{i-1}}{\mathit{\boldsymbol{p}}_i}}}} \right|, {\rm{ }}\;\;\;\;\;\;\;\;\;\;{\rm{ }}\left| {{\theta _{\mathit{\boldsymbol{r}}_i^t}}-{\theta _{{\mathit{\boldsymbol{p}}_{i - 1}}{\mathit{\boldsymbol{p}}_i}}}} \right|\; \le \;{180^ \circ }\\ {360^ \circ } - \left| {{\theta _{\mathit{\boldsymbol{r}}_i^t}} - {\theta _{{\mathit{\boldsymbol{p}}_{i - 1}}{\mathit{\boldsymbol{p}}_i}}}} \right|, {\rm{ }}\left| {{\theta _{\mathit{\boldsymbol{r}}_i^t}} - {\theta _{{\mathit{\boldsymbol{p}}_{i - 1}}{\mathit{\boldsymbol{p}}_i}}}} \right|\; > {180^ \circ } \end{array} \right. $ | (7) |
通过式(7) 计算出βit后,本文采用式(8) 来计算方向权重:
| $ Dir_{_i}^{^t}{\rm{ = }}\left( {1 + {\rm{cos}}\beta _i^t} \right)/2;{\rm{ }}\beta _i^t \in [-{0^ \circ }, {\rm{ }}{180^ \circ }] $ | (8) |
全局匹配算法的正确率一般比实时匹配算法高,原因是全局算法考虑了历史GPS轨迹点及路匹配段的信息。而实时匹配算法很多都只考虑了当前GPS轨迹点及其候选路段的信息,没有考虑历史因素。本文提出连通性权重来描述当前GPS轨迹点与历史GPS轨迹点及匹配路段的时空关系。
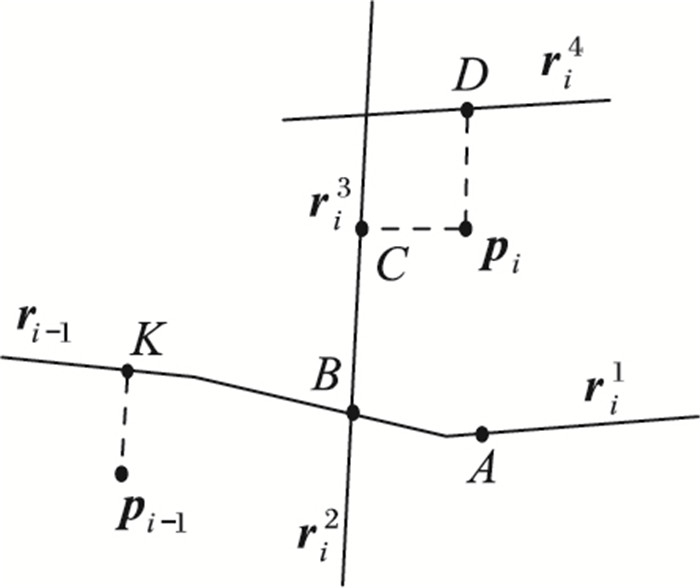
将GPS轨迹点垂直投影到路段时,如果投影点在路段的延长线上,那么就将靠近GPS轨迹点的路段端点作为其投影点。如图 7,历史GPS轨迹点pi-1匹配到路段ri-1, 投影点为K。当前GPS轨迹点pi有四条候选路段ri1、ri2、ri3和ri4, 对应投影点为A、B、C、D。根据pi-1、pi的速度p.v和时间戳p.t信息,可以计算出车辆从pi-1.t到pi.t期间实际行驶距离ltravel。利用Dijkstra算法,计算出路网中投影点K到投影点A、B、C、D的匹配距离lmatcht分别为:lmatch1=|KA|、lmatch2=|KB|、lmatch3=|KC|, lmatch4=|KD|。
|
图 7 连通性权重 Figure 7 Connectivity weight |
设lmatcht表示从pi-1在其匹配路段ri-1上投影点到pi在其候选路段rit上投影点间在路网中的最短距离。ltravel与lmatcht值越接近,表明pi匹配到候选路段rit的可能性越大,连通性权重也越大。pi-1匹配路段rs到pi候选路段rit连通性权重Conrits→t的计算公式为:
| $ Con_{\mathit{\boldsymbol{r}}_i^t}^{s \to t} = {{\rm{e}}^{-{\rm{ }}\alpha \times \left( {|{l_{{\rm{travel}}}}-l_{{\rm{match}}}^t|} \right)/A}} $ | (9) |
其中:A=min{ltravel, lmatcht}, 当车辆静止时计算得到的ltravel为0,这时令A=1 m;α是一个常数,由于GPS精度等原因,针对实验轨迹计算出的|ltravel-lmatcht|误差为0~10 m,α用于调节对该误差的敏感度。
对于ltravel的计算,关键是求出pi-1到pi间的平均速度
1) GPS轨迹点采样间隔为1~5 s。由于时间间隔短,速度变化一般不大,
2) GPS轨迹点采样间隔大于5 s。这时用第一种方式计算平均速度就不合适了,此时ltravel近似等于相邻GPS轨迹点间的欧拉距离,即ltravel=lpi-1→pi。
3) 当车辆在经过隧道或立交桥时,GPS信号丢失导致采样时间间隔变大,可能长达数分钟。这期间车辆的速度变化可能会很大,这时ltravel=lpi-1→pi。
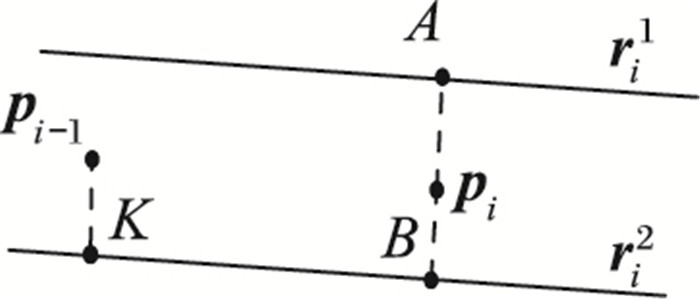
连通性权重还能避免对平行路段的错误匹配。如图 8,ri1和ri2是pi的两条同方向平行候选路段,假设pi-1匹配到路段ri2, 那么pi匹配到ri2的连通性权重将比匹配到ri1大得多,表明pi匹配到ri2的可能性更高。
|
图 8 连通性权重对平行道路匹配的影响 Figure 8 Influence of connectivity weight on parallel road's matching |
参考文献[4],本文选择以下函数来计算各个权重的权重系数,对于不同的GPS轨迹点进行匹配时将采用不同权重系数。
距离权重系数根据GPS轨迹点的水平精度衰减因子hdop来确定,pi.hdop越小,距离权重越可靠。pi的候选路段rit的距离权重系数为:
| $ \begin{array}{l} {W_{dis{t_i}}} = \\ \left\{ \begin{array}{l} 0, {\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{p}}_i} . hdop \ge HDO{P_2}\\ \frac{{{\mathit{\boldsymbol{p}}_i} . hdop-HDO{P_1}}}{{HDO{P_2}-HDO{P_1}}}{\rm{, }}HDO{P_1} < {\mathit{\boldsymbol{p}}_i} . hdop < HDO{P_2}\\ 1, {\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{p}}_i} . hdop \le HDO{P_1} \end{array} \right. \end{array} $ | (10) |
车辆速度pi.v越大,GPS轨迹点的方向pi.comp越可靠;反之,当pi.v很低时,pi.comp将变得不可靠[16]。由于方位权重考虑了历史信息,因此方位权重系数还受到pi-1.v的作用。rit的方位权重系数为:
| $ \begin{array}{l} {W_{hea{d_i}}} = \\ \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{p}}_i}.v < {V_1}或 {\mathit{\boldsymbol{p}}_{i-1}}.v < {V_1}\\ 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{p}}_i}.v > {V_2} 或 {\mathit{\boldsymbol{p}}_{i-1}}.v > {V_2}\\ \left( {{\mathit{\boldsymbol{p}}_i}.v-{V_1}} \right)/\left( {{V_2} - {V_1}} \right), \;\; 其他 \end{array} \right. \end{array} $ | (11) |
对于方向权重系数,考虑pi和pi-1间欧拉距离lpi-1→pi与平均行驶距离lmean的关系,lpi-1→pi越大,方位权重受误差影响越小。rit的方向权重系数为:
| $ {W_{di{r_i}}} = \left\{ \begin{array}{l} {\rm{1, }}\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\;\;\;\;\;{\rm{ }}{l_\mathit{\boldsymbol{p}}}_{_{i-1} \to {\mathit{\boldsymbol{p}}_i}} > {l_{{\rm{mean}}}}\\ {l_\mathit{\boldsymbol{p}}}_{_{i-1} \to {\mathit{\boldsymbol{p}}_i}}/{l_{{\rm{mean}}}}{\rm{, }}{l_\mathit{\boldsymbol{p}}}_{_{i-1} \to {\mathit{\boldsymbol{p}}_i}} \le {l_{{\rm{mean}}}} \end{array} \right. $ | (12) |
对于连通性权重系数,考虑连通性权重的阈值Conth与rit的连通性权重Conrits→t的关系,Conrits→t值大于Conth则认为rit的连通性符合匹配路段的条件。rit的连通性权重系数为:
| $ {W_{co{n_i}}} = \left\{ \begin{array}{l} {\rm{1, }}\;\;\;\;\;\;\;\;\;\;\;Con_{\mathit{\boldsymbol{r}}_i^t}^{s \to t} \ge Co{n_{{\rm{th}}}}\\ Con_{\mathit{\boldsymbol{r}}_i^t}^{s \to t}, \;\;Con_{\mathit{\boldsymbol{r}}_i^t}^{s \to t} < Co{n_{{\rm{th}}}} \end{array} \right. $ | (13) |
以往实时匹配算法一般分三个阶段[2]:初始位置匹配、跟踪匹配、路口路段匹配。路口路段匹配阶段需要进行路口检测,这无疑增加了算法的复杂性。本文算法将跟踪匹配和路口路段匹配合并为一个阶段,不再进行路口检测以算法简化模型,即分为两个阶段:初始位置匹配、后续位置匹配。
得到点pi的候选路段Ci={ri1, ri2, …, rik}后,按式(14)、(15) 计算候选路段rit的总得分Stotalit。
| $ {{{S}}_{total_i^t}} = {{{S}}_{dist_i^t}} + {{{S}}_{head_i^t}} + {{{S}}_{dir_i^t}} + {{{S}}_{con_i^t}} $ | (14) |
| $ \left\{ \begin{array}{l} {S_{dist_i^t}} = {W_{dist_i^t}} \times Dist_i^t\\ {S_{head_i^t}} = {W_{head_i^t}} \times Head_i^t\\ {S_{dir_i^t}} = {W_{dir_i^t}} \times Dir_i^t\\ {S_{con_i^t}} = {W_{con_i^t}} \times Co{n_{\mathit{\boldsymbol{r}}_{s \to t}^i}} \end{array} \right. $ | (15) |
如果初始位置匹配错误,可能导致后续GPS轨迹点连续失配,因此本文选择相对保守的方式进行延迟匹配。在初始位置匹配阶段,假设匹配两个连续GPS轨迹点p1、p2, 候选路段分别为C1={r11, r12, r13}及C2={r21, r22}。分别计算出所有可能匹配组合中p2各候选路段的总得分:Stotal2(r11, r21), Stotal2(r12, r21), Stotal2(r13, r21), Stotal2(r11, r22), Stotal2(r12, r22), Stotal2(r13, r22)。Stotal2(r1s, r2t)表示p1匹配到路段r1s时, p2候选路段r2t的总得分。然后选择得分最高和次高的两个匹配组合,假设为Stotal2(r12, r21), Stotal2(r13, r21), 如果:
| $ S_{tota{l_2}}^{}(\mathit{\boldsymbol{r}}_1^2, \mathit{\boldsymbol{r}}_2^1)-{\rm{S}}_{tota{l_2}}^{}(\mathit{\boldsymbol{r}}_1^3, \mathit{\boldsymbol{r}}_2^1) \ge {K_{{\rm{init}}}} $ | (16) |
那么就将p1匹配到r12, 将p2匹配到r21。如果不满足该条件则跳过p1的匹配,按同样的方法处理p2、p3直到满足条件才结束初始匹配阶段。Kinit为初始匹配阶段的置信度水平。
2.4.2 后续位置匹配在计算出pi所有候选路段的总得分Stotalit后,将得分按从高到低排序, 得到总得分最高和次高的两条路段rif, ris, 对应总得分分别为Stotalif和Stotalis。如果二者满足以下条件,则将pi匹配到路段rif; 否则跳过该点的匹配,并保持车辆位置不变。
| $ {S_{total_i^f}}-{S_{total_i^s}} \ge {K_i} $ | (17) |
其中Ki为匹配置信度水平,该值越大匹配正确的信心越高。如果pi仅有一条候选路段,则直接将点匹配到该路段。参考文献[4],本文用式(18) 计算置信度Ki, 匹配不同GPS轨迹点采用不同的置信度。
在计算出pi的匹配路段ri后,将pi垂直投影到ri, 投影点就是车辆当前的位置。如果投影点在ri的延长线上,则将ri更靠近pi的端点作为车辆当前的位置。
| $ \begin{array}{l} {K_i} = \frac{1}{{{W_{dis{t_i}}} + {W_{head}}_{_i} + {W_{di{r_i}}} + {W_{co{n_i}}}}} \times \\ \left( {{W_{dis{t_i}}} \times \frac{{\left| {Dist_i^{{\rm{fir}}} - Dist_i^{{\rm{sec}}}} \right|}}{{Dist_i^{{\rm{fir}}} + Dist_i^{{\rm{sec}}}}}} \right. + {W_{hea{d_i}}} \times \frac{{\left| {Head_i^{{\rm{fir}}} - Head_i^{{\rm{sec}}}} \right|}}{{Head_i^{{\rm{fir}}} + Head_i^{{\rm{sec}}}}} + \\ {W_{di{r_i}}} \times \frac{{\left| {Dir_i^{{\rm{fir}}} - Dir_i^{{\rm{sec}}}} \right|}}{{Dir_i^{{\rm{fir}}} + Dir_i^{{\rm{sec}}}}} + \left. {{W_{co{n_i}}} \times \frac{{\left| {Con_i^{{\rm{fir}}} - Con_i^{{\rm{sec}}}} \right|}}{{Con_i^{{\rm{fir}}} + Con_i^{{\rm{sec}}}}}} \right) \end{array} $ | (18) |
其中:Distifir、Headifir、Dirifir和Conifir是pi总得分最高候选路段rifir的四个权重值;Distisec、Headisec、Dirisec和Conisec是pi总得分排第二的候选路段risec的四个权重值。
3 算法评估与结果 3.1 实验环境准备地图数据为开源地图OpenStreetMap;GPS轨迹为三条重庆市区公交车轨迹,包含道路类型有立交桥、隧道等特殊路段,轨迹点采集时间间隔为1~3 s;地理信息系统(Geographic Information System,GIS)引擎为github开源项目GraphHopper, 用于计算候选路段方向、最短路径等。实验平台基于Java实现,平台硬件配置为:内存4 GB,CPU型号为Intel Core i3-2310M 2.1 GHz。
由于OpenStreetMap地图数据并不完备,一些非主干道数据存在缺失,导致GPS轨迹中部分轨迹点无法找到正确的匹配路段,因此将这部分GPS轨迹点提前去除。表 1中列举了实验轨迹的一些特征信息。根据三条轨迹中所有GPS轨迹点的pi.v和pi.hdop确定距离权重系数函数和方位权重系数函数中的常数,利用MAD公式计算得到:V1=2.35 m/s, V2=3.35 m/s, HDOP1=4, HDOP2=7。
| 表 1 GPS轨迹数据特征 Table 1 Characteristics of GPS trajectories |
表 2是本文提出算法的性能评估结果。可以看到平均95.6%的GPS轨迹点被匹配到了道路上,表明计算出的平均延迟比较可靠,不会因为太多轨迹点未被匹配到道路而导致算法长时间不更新车辆位置。
| 表 2 本文提出算法的性能评估结果 Table 2 Performance evaluation results by proposed map matching algorithm |
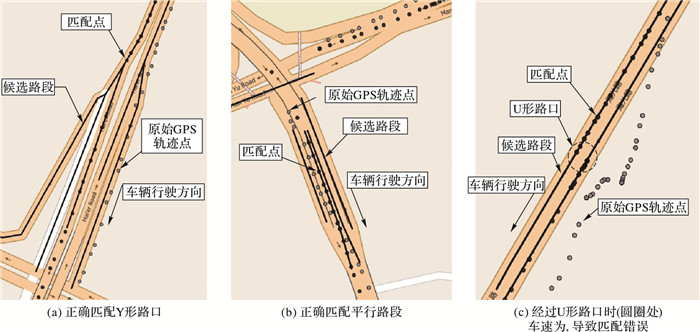
如图 9(a),从轨迹点的候选路段可以看出车辆经过了一个Y形路口,尽管GPS轨迹点距离误差很大,但算法仍匹配正确,而以往实时匹配算法在Y形路口很容易发生误匹配[1]。如图 9(b),从立交桥处轨迹点的候选路段平行且方向一样可以看出这是平行路段,最终算法将轨迹点匹配到了正确路段。如图 9(c),车辆经过U形路口(圆圈处)时,由于连续多个GPS轨迹点速度为0,导致匹配错误轨迹点的方向权重和方位权重都为0。而且在U形路口,两条候选路段与历史匹配路段都能连通,导致连通权重也失效。最终起作用的只有距离权重,但是GPS轨迹点距离误差很大,因而导致了匹配错误。
|
图 9 实验匹配情况 Figure 9 Experimental results of map matching |
表 3将本文算法与其他几种实时地图匹配算法进行了对比。本文算法匹配正确率比以往基于权重匹配算法都高,甚至超过了高级匹配算法[7]基于HMM的匹配准确率。
| 表 3 本文提出算法与已有算法性能比较 Table 3 Comparison of the proposed algorithm with other exsiting algorithms |
在总结以往全局地图匹配算法和实时匹配算法的优缺点后,本文提出了一种改进的基于动态权重的实时地图匹配算法。基于对道路网和GPS轨迹时空信息的分析,该算法建立了由四个权重组成的权重模型:1) 距离权重,即GPS轨迹点到候选路段距离;2) 方位权重,即相邻GPS轨迹点瞬时方向的变化程度与候选路段相对上一条匹配路段方向的变化程度间的相似性;3) 方向权重,即相邻GPS轨迹点间连线的方向与候选路段方向间的相似性;4) 连通性权重,即连通性候选路段和上一条匹配路段间的连通性。然后利用GPS轨迹点的速度、水平精度衰减因子hdop等信息建立各权重对应的动态权重系数函数,进而得到每条候选路段的总得分。最后,算法根据每个轨迹点的匹配置信度水平得到最佳匹配路段。
本文基于总长36 km的3条真实轨迹对算法进行评估,结果表明:1) 本文算法能正确匹配Y形道路、平行道路,甚至能对立交桥的弯道有比较好的匹配效果,然而在U形路口处匹配错误表明算法在对低速下行驶车辆的匹配仍有待提高;2) 本文算法的平均匹配正确率为97.31%,优于现有的基于权重匹配算法,单个轨迹点匹配平均延迟为17.9 ms,满足ITS应用对准确性和实时性的要求。研究也说明充分利用路网和GPS轨迹点信息,权重匹配算法也可以达到高级算法的匹配正确率,但由于它不像高级算法那样复杂,实时性能更高。但本文算法的性能也可能受到了实验平台和电子地图精度的限制,以及低速下的匹配精度仍有进一步提升的空间,这将成为未来的研究方向。
| [1] | QUDDUS M A, OCHIENG W Y, NOLAND R B. Current map-matching algorithms for transport applications:State-of-the art and future research directions[J]. Transportation Research Part C:Emerging Technologies, 2007, 15(5): 312-328. DOI:10.1016/j.trc.2007.05.002 |
| [2] | HASHEMI M, KARIMI H A. A critical review of real-time map-matching algorithms:Current issues and future directions[J]. Computers, Environment and Urban Systems, 2014, 48: 153-165. DOI:10.1016/j.compenvurbsys.2014.07.009 |
| [3] | KIM J-S. Node based map matching algorithm for car navigation system[C]//Proceedings of the 29th International Symposium on Automotive Technology & Automation. Croydon, England:Automotive Automation Ltd., 1996. http://trid.trb.org/view/642362 |
| [4] | HASHEMI M, KARIMI H A. A weight-based map-matching algorithm for vehicle navigation in complex urban networks[J]. Journal of Intelligent Transportation Systems, 2016, 20(6): 573-590. DOI:10.1080/15472450.2016.1166058 |
| [5] | VELAGA N R, QUDDUS M A, BRISTOW A L. Developing an enhanced weight-based topological map-matching algorithm for intelligent transport systems[J]. Transportation Research Part C:Emerging Technologies, 2009, 17(6): 672-683. DOI:10.1016/j.trc.2009.05.008 |
| [6] | QUDDUS M A, OCHIENG W Y, ZHAO L, et al. A general map matching algorithm for transport telematics applications[J]. GPS Solutions, 2003, 7(3): 157-167. DOI:10.1007/s10291-003-0069-z |
| [7] | GOH C Y, DAUWELS J, MITROVIC N, et al. Online map-matching based on hidden Markov model for real-time traffic sensing applications[C]//ITSC 2015:Proceedings of the 201215th International IEEE Conference on Intelligent Transportation Systems. Piscataway, NJ:IEEE, 2012:776-781. https://www.researchgate.net/publication/261150591_Online_map-matching_based_on_Hidden_Markov_model_for_real-time_traffic_sensing_applications |
| [8] | LOU Y, ZHANG C, ZHENG Y, et al. Map-matching for low-sampling-rate GPS trajectories[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2009:352-361. https://www.researchgate.net/publication/221589740_Map-matching_for_low-sampling-rate_GPS_trajectories |
| [9] | NEWSON P, KRUMM J. Hidden Markov map matching through noise and sparseness[C]//GIS' 09:Proceedings of the 17th ACM SIGSPATIAL international conference on advances in geographic information systems. New York:ACM, 2009:336-343. https://www.researchgate.net/publication/221589790_Hidden_Markov_map_matching_through_noise_and_sparseness |
| [10] | 郑学远. 基于模糊逻辑的综合地图匹配方法研究与实现[D]. 北京: 北京交通大学, 2014: 29-53. (ZHENG X Y. The research and realization of integrated map matching method based on fuzzy logic[D]. Beijing:Beijing Jiaotong University, 2014:29-53.) http://cdmd.cnki.com.cn/Article/CDMD-10004-1014374310.htm |
| [11] | QUDDUS M A, NOLAND R B, OCHIENG W Y. A high accuracy fuzzy logic based map matching algorithm for road transport[J]. Journal of Intelligent Transportation Systems, 2006, 10(3): 103-115. DOI:10.1080/15472450600793560 |
| [12] | 肖维丽, 岳春生, 奚玲. 基于高程的改进D-S证据理论地图匹配算法[J]. 计算机应用与软件, 2015, 32(7): 262-265. (XIAO W L, YUE C S, XI L. Improved D-S evidence theory map maching algorithm based on elevation information[J]. Computer Applications and Software, 2015, 32(7): 262-265.) |
| [13] | 夏州. GPS车辆导航中的数据处理与地图匹配研究[D]. 北京: 北京交通大学, 2009: 37-40. (XIA Z. Research of GPS data processing and map matching in vehicle navigation system[D]. Beijing:Beijing Jiaotong University, 2009:37-40.) http://cdmd.cnki.com.cn/Article/CDMD-10004-2009146498.htm |
| [14] | TANG Y, ZHU A D, XIAO X. An efficient algorithm for mapping vehicle trajectories onto road networks[C]//SIGSPATIAL' 12:Proceedings of the 20th International Conference on Advances in Geographic Information Systems. New York:ACM, 2012:601-604. https://www.researchgate.net/publication/262366274_An_efficient_algorithm_for_mapping_vehicle_trajectories_onto_road_networks |
| [15] | TAYLOR G, BLEWITT G, STEUP D, et al. Road reduction filtering for GPS-GIS navigation[J]. Transactions in GIS, 2001, 5(3): 193-207. DOI:10.1111/tgis.2001.5.issue-3 |
| [16] | OCHIENG W Y, QUDDUS M, NOLAND R B. Map-matching in complex urban road networks[J]. Brazilian Journal of Cartography, 2003, 55(2): 1-14. |




