2. 重庆信科设计有限公司, 重庆 400065
2. Chongqing Information Technology Designing Company Limited, Chongqing 400065, China
数据挖掘是从大量的数据中挖掘出隐含的、未知的、用户可能感兴趣的知识和规则的过程。关联规则是数据挖掘中非常重要的一个研究方向,能够找到事务之间隐含的人们可能感兴趣的规则,从而为人们带来巨大的价值。在当今大数据时代,如何在海量的数据中挖掘出有价值的关联规则显得尤为重要。
频繁模式挖掘是关联规则挖掘中最重要的一步,利用频繁模式可以较容易地推导出关联规则。Apriori算法是频繁模式挖掘的经典算法,由Agrawal等[1]于1994年提出。该算法利用逐层迭代的思想,由频繁k-1-项集与自身进行连接、剪枝等步骤产生频繁k-项集,从而挖掘出所有的频繁模式。但是Apriori算法存在多次扫描数据库以及产生大量候选项集的问题,对此学者们提出了一系列改进算法。例如,基于hash技术的直接散列剪枝(Direct Hashing and Pruning, DHP)算法[2]将产生的候选项集通过hash函数散列到不用的hash桶中,通过对hash桶中的项目进行计数,剔除不符合支持度要求的项目,从而得到频繁项集。DHP算法本质上是以空间换取时间的算法,面对大规模数据集时,算法效率将会急剧下降。基于抽样(Sampling)技术的频繁模式挖掘算法[3]首先从数据库中抽取样本数据进行运算后得到频繁模式,然后用数据库中剩余数据检验所挖掘频繁模式的正确性。抽样技术运行速度快,时间效率高,能够快速挖掘出频繁模式,但由于Sampling算法利用随机抽样法进行采样,必然伴随数据扭曲(data skew)问题,导致挖掘结果具有较大的不确定性。BitTableFI算法[4]使用位表压缩数据库,然后使用位表数据结构及二进制的与或操作迭代挖掘频繁项集,在产生候选项集及支持度计算方面均比Apriori算法更有效率。但是BitTableFI算法存在产生大量候选项集以及重复计算支持的问题,挖掘效率仍有待提高。赵学健等[5]提出了挖掘频繁项集的正交链表算法(Orthogonal List Algorithm, OLA)。该算法首先将事务数据库转化为一个布尔矩阵,然后依据布尔矩阵构造正交链表,因此可以通过对正交链表进行操作来挖掘频繁项集。除此之外,该算法优化了连接和剪枝操作,提高了算法效率。OLA算法只需扫描数据库一次,利用正交链表的优势可以快速挖掘出频繁项集。虽然该算法利用正交链表这一能够快速遍历的数据结构,但是该算法在数据量较大或者项集过长时需要耗费大量的内存,空间效率有待提高。
针对Apriori算法及其改进算法存在多次扫描数据库、算法效率不高的问题,Han等[6]提出了采用分治策略的频繁模式增长(Frequent Pattern growth,FP-growth)算法。该算法使用频繁模式树(Frequent Pattern tree,FP-tree)代表数据库,然后利用递归构建条件FP-tree来挖掘频繁项集。由于精简的数据结构FP-tree能够完整代表事务数据库中的项,因此避免了对数据库的多次扫描,挖掘效率较Apriori算法提升明显。但是FP-growth算法需要两次扫描数据库来构建FP-tree,同时在挖掘过程中需要构建条件模式基和条件模式树,从而会带来巨大的时间与空间开销。针对FP-growth算法需要两次扫描数据库以及需要扫描不含频繁项的事务的问题,李也白等[7]提出了一种基于改进的FP-tree的频繁模式挖掘算法。该算法深入分析了FP-tree的性质与特点,对FP-tree的构造过程进行了改进,同时还利用哈希表来进行辅助存储,提高了挖掘效率;但是该算法依旧采用模式增长来挖掘频繁模式,挖掘效率有待提高。
Eclat算法使用垂直数据结构挖掘频繁项集,能够利用交集运算快速求得项集的支持度,提高挖掘效率[8]。但是Eclat利用候选项集的子集产生新的候选项集,这种方法产生的候选项集数量较Apriori更多,大大影响了算法的效率。除此之外,当Tidset数量庞大时,不仅会占用大量内存,而且其交集运算会消耗大量时间,时间与空间开销都很大。在此基础上,Deng等[9]提出了prepost算法。该算法使用比FP-tree更精简的数据结构——前序后序编码树(Pre-order and Post-order Code tree,PPC-tree),前序后序两次遍历PPC-tree后,可以得到每个节点的pre-order和post-order,从而得到其对应的N-list。通过连接两个频繁k-1项集的N-list可以快速挖掘出频繁项集。但是prepost算法中PPC-tree构建复杂,没有对搜索空间进行剪枝,算法效率仍有待提高。Vo等[10]在N-list基础上结合包含索引对搜索空间进行剪枝操作,提出了NSFI算法。该算法较prepost算法性能有一定提升,但是在面对大型数据库时,仍旧存在建树复杂、挖掘效率低的问题。
针对现有的频繁模式挖掘算法存在建树复杂、挖掘效率低等问题,本文提出了一种新的频繁模式挖掘算法——基于构造链表(Building list,B-list)的频繁模式挖掘(B-list Frequent Pattern Ming,BLFPM)算法。BLFPM首先扫描一次数据库,得到所有的频繁1-项集,将数据库中所有事务的项按频繁1-项集的支持度降序进行排列;然后通过构建TB-tree得到频繁1-项集对应的B-list,通过对B-list进行连接操作即可快速得到候选项集的支持度,避免了频繁扫描数据库。在B-list的连接操作中,BLFPM使用了一种线性时间复杂度算法,有效解决了连接B-list的高复杂度问题; 除此之外,BLFPM使用集合枚举树代表搜索空间,并使用子集非频繁策略进行剪枝操作,减小了算法的搜索空间,提高了算法的执行速度。实验结果表明,BLFPM可以有效提高频繁模式挖掘的时间和空间效率。
1 相关概念 1.1 问题描述设I={i1, i2, …, im}是事务数据库中所有不同项目的集合,DB={T1, T2, …, Tn}是包含n个事务的数据库,事务Tk={i1, i2, …, it}代表不同项目的集合。设事务数据库DB如表 1所示(支持度取0.3)。
| 表 1 事务数据库DB Table 1 An transaction database DB |
定义1 k-项集。对于集合X∈I, 称集合X为一个项集,包含k个项目的项集称为k-项集。
定义2 支持度。对于给定的事务数据库DB, 项集X的支持度是指DB中包含X的事务数与事务总数之比,记为σ(X)。设事务总数为|DB|, 包含项集X的事务数为sup(X),则X的支持度σ(X)=sup(X)/|DB|。
定义3 频繁k-项集。对于给定的事务数据库DB, min-sup为用户给定的最小支持度,如果sup(X)≥min-sup×|DB|, 则称X为频繁项集。如果X为k-项集,则称为频繁k-项集。
性质1 频繁项集的子集一定是频繁项集;非频繁项集的超集一定是非频繁项集。
有了上述定义与性质,频繁模式挖掘问题就可以描述为利用性质1找出事务数据库中所有满足用户最小支持度的项集问题。
1.2 TB-tree针对现有的频繁模式挖掘算法使用的FP-tree[5]、PPC-tree[9]等数据结构挖掘效率低、建树复杂等问题,本文算法采用了一种构造遍历树(Traversal when Building,TB-tree)结构[11]。TB-tree由root节点和项目的前缀子树构成。项目的前缀子树的每个节点包含五个部分:item-name代表项目名称;count代表经过这一节点的事务数目;parent-pointer指向当前节点的父节点;start-build代表此节点开始构造顺序;finish-build代表此节点结束构造的顺序。
同FP-tree相比, TB-tree不仅不需要指向具有相同节点名称的指针node-link和存储频繁项集的头表header table,而且TB-tree主要用于构建B-list,在构建完成B-list之后,可以从内存中删除。因此,使用TB-tree进行频繁模式挖掘,不仅比使用FP-tree具有更快的建树速度,而且内存占用少,时间与空间开销都更少。与PPC-tree相比,TB-tree的节点中不含pre-order和post-order,不需要通过前序和后序两次遍历得到每个节点的pre-order和post-order。TB-tree使用start-build与finish-build代替pre-order和post-order,其值能够依据节点在TB-tree的构建顺序得到,因此TB-tree可以在一次构建中完成,不需要额外的遍历操作,比PPC-tree的建立具有更高的时间效率。文献[11]利用TB-tree对数据库进行压缩,然后在此基础上使用动态支持度阈值和包含索引策略来挖掘top-rank-k频繁模式,而本文主要在TB-tree的基础上通过采取有效的连接与剪枝策略来挖掘频繁模式,给出了一种快速频繁模式挖掘算法。TB-tree的构建算法如算法1所示。
算法1 构建TB-tree。
输入 事务数据库DB;
输出 TB-tree,L1
1) 扫描DB, 得到频繁1-项集L1,将其按项目支持度降序排列, 将DB中的事务的项按L1的顺序排列, 创建root节点,初始化全局变量start=0, finish=0; p与q为数据库中的项目,Node为TB-tree的节点
2) for each different first item p in DB do
3) Call BuildTree(p, Node)
4) end for
5) end
function BuildTree(p, parent)
a) Let TP be a list of transactions in DB which contain prefix p
b) Creat node N:
N.item-name=item-name of the last item in p
N.count=count of transactions in TP
N.parent=parent
c) N.start-build=++start
d) for each different first item q in TP do
e) Call buildTree(p∪q, N)
f) end for
g) N.finish-build=++finish
end function
应用算法1构建表 1所示数据库的TB-tree如图 1所示。
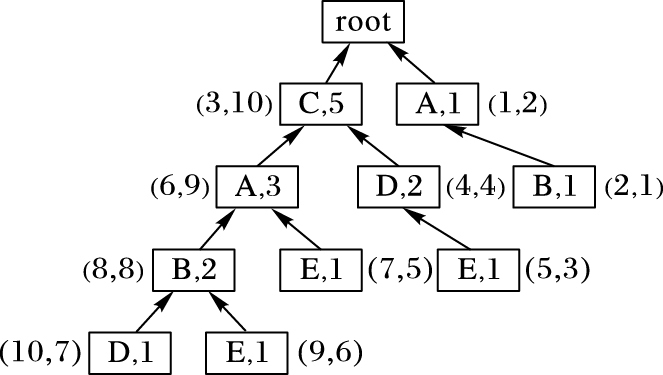
|
图 1 DB对应的TB-tree Figure 1 TB-tree of the DB |
依据TB-tree,本节给出B-list的定义与性质。为了定义B-list,首先给出B-info-code的定义。
定义4 B-info-code。对于TB-tree中的每一个节点N, [(N.start-build,N.finish-build),N.count]称为节点N的B-info-code。
性质2 对于两个不同的节点N1和N2,当且仅当N1.start-build<N2.start-build与N1.finish-build>N2.finish-build同时成立时,N1才是N2的祖先节点。
证明 由TB-tree构建算法可知,祖先节点总是先于孩子节点构建,因此,祖先节点对应的start-build值总是小于孩子节点的start-build值;又因为祖先节点总是晚于孩子节点构建完成,因此祖先节点对应的finish-build值总是大于孩子节点的finish-build值。
性质2还表明TB-tree中每一个节点与其B-info-code是一一对应的:一个节点对应唯一的B-info-code,一个B-info-code亦对应唯一的节点。因此节点的孩子祖先关系亦能由其对应的B-info-code来表示,给出如下定义。
定义5 B-info-code的孩子祖先关系。设X1:[(s1, f1),c1]为节点N1的B-info-code,X2:[(s2, f2),c2]为节点N2的B-info-code,当且仅当s1<s2与f1>f2同时成立时,X1是X2的祖先。
定义6 1-项集的B-list。对于给定的TB-tree与节点N,所有名为N的节点的所有B-info-code构成的集合称为其对应的B-list,记为BLN。其中所有B-info-code按照start-build递增顺序排列。
通过遍历构建完成的TB-tree,可以得到所有频繁1-项集的B-list。遍历图 1所示TB-tree得到的所有频繁1-项集的B-list如表 2所示。
定义7 2-项集的B-list。对于频繁1-项集L1中不同的项i1,i2,i1在i2之前,i2对应的B-list为{[(s11, f11),c11],[(s12, f12),c12],…,[(s1n, f1n),c1n]}, i2对应的B-list为{[(s21, f21),c21],[(s22, f22),c22],…,[(s2m, f2m),c2m]},则i1i2的B-list可由如下计算-合并规则确定:
计算:对于任意[(s1i, f1i),c1i](1≤i≤n),判断其是否为[(s2j, f2j),c2j] (1≤j≤m)的祖先:如果是,将[(s1i, f1i),c2j]添加到i1i2的B-list中; 如果不是,则进行下一次判断。经过此步骤可以得到i1i2的B-list。
合并:对于i1i2的B-list中具有相同start-build与finish-build值的B-info-code{[(s1, f1),c1], [(s1, f1),c2], …, [(s1, f1),cn]}, 将其合并为[(s1, f1),c1+c2+…+cn]。
例如,连接项集C与D的B-list,首先比较[(3,10),5]与[(4,4),2],发现[(3,10),5]是[(4,4),2]的祖先,则将[(3,10),2]加入项集CD的B-list。同时[(3,10),5]也是[(10,7),1]的祖先,将[(3,10),1]也加入到CD的B-list中,然后对CD的B-list进行合并操作,得到CD的B-list为[(3,10),3]。
定义8 k-项集的B-list。对于频繁k-1-项集X=ixi1i2…ik-2与Y=iyi1i2…ik-2,其中k≥3。项集X对应的B-list为{[(s11, f11),c11],[(s12, f12),c12],…[(s1n, f1n),c1n]}, 项集Y对应的B-list为{[(s21, f21),c21],[(s22, f22),c22],…,[(s2m, f2m),c2m]},则ixiyi1i2…ik-2的B-list可由如下计算-合并规则确定。
计算:对于任意[(s1i, f1i),c1i](1≤i≤n),判断其是否为[(s2j, f2j),c2j] (1≤j≤m)的祖先:如果是,将[(s1i, f1i),c2j]添加到k-项集ixiyi1i2…ik-2的B-list中;如果不是,则进行下一次判断。经过此步骤可以得到k-项集ixiyi1i2…ik-2的B-list。
合并:对于k-项集ixiyi1i2…ik-2的B-list中具有相同start-build与finish-build的{ [(s1, f1),c1], [(s1, f1),c2], …, [(s1, f1),cn]}, 将其合并为[(s1, f1),c1+c2+…+cn]。
性质3 设项集X的B-list为{[(s1, f1),c1],[(s2, f2),c2],…,[(sn, fn),cn]}, 则项集X的支持数sup(X)=c1+c2+…+cn。
证明 由于项集X的B-list中每一个B-info-code[(s, f),c]均与TB-tree中名为X的节点相对应,因此项集X的支持数为对应TB-tree中所有同名节点的count值之和,因此sup(X)=c1+c2+…+cn。
2 BLFPM算法结合第1章的TB-tree与B-list结构,本章提出一种新的频繁模式挖掘算法——BLFPM算法。BLFPM使用B-list表示频繁项集,通过对B-list进行操作可以快速挖掘出所有的频繁项集。针对Apriori算法在计算候选项集支持度时需要多次扫描数据库的问题,BLFPM通过连接对应项集的B-list,可以直接得到候选项集的支持度,不需要对数据库进行扫描;针对B-list连接的高复杂度问题,BLFPM给出了一种线性时间复杂度的连接方法,大大提高了算法时间效率;对于搜索空间大的问题,BLFPM使用集合枚举树代表搜索空间并使用子集非频繁剪枝策略,有效减小了候选项集的搜索空间,提高了算法的执行速度。BLFPM主要包含四个步骤:1) 扫描数据库,得到频繁1-项集L1,构建TB-tree;2) 遍历TB-tree, 得到频繁1-项集L1对应的B-list BL1; 3) 挖掘出所有的频繁2-项集L2;4) 挖掘出所有的频繁k-项集(k>2)。其中步骤1的算法已由第1章给出,本章主要介绍后面三个步骤。
2.1 计算BL1与挖掘频繁2-项集L2按照start-build顺序遍历TB-tree,便可得到所有频繁1-项集L1的B-list。文献[12]表明,基于Apriori算法改进的频繁模式挖掘算法在挖掘频繁2-项集时,由于需要连接频繁1-项集,从而会产生大量的候选2-项集,时间和空间开销都很大,会严重影响算法的时间和空间效率。因此,本节提出了一种基于TB-tree的频繁2-项集快速挖掘算法并将其应用到BLFPM算法中。该算法按照start-build的顺序遍历TB-tree,对于每一个节点N, 设NA为其祖先节点,只需要将其与其祖先进行连接,便可得到相应的候选2-项集NNA。使用这种方法不需要产生没有祖先-孩子关系的候选2-项集,减少了候选2-项集的数量,提高了算法的时间效率。将所有候选2-项集的支持度与用户给定的支持度进行比较,删除不符合支持度要求的2-项集,就可以得到所有的频繁2-项集L2。为了提高BLFPM算法的执行效率,将其步骤2与步骤3在同一次遍历TB-tree中完成,如算法2所示。
算法2 挖掘BL1与频繁2-项集L2。
输入 TB-tree,L1;
输出 BL1,L2。
1) Creat array=int [L1.length][L1.length], L1[k].sequence=k
2) for each node N of TB-tree accessed by start-build traversal do
3) if (N.item-name=L1[k]) then
4) insert [(N.start-build, N.finish-build), N.count] into BL1[k]
5) end if
6) for each node NA,ancestor of N do
7) array [N.sequence][NA.sequence]+=N.count
8) end for
9) end for
10) for each element in array do
11) if(array[i][j]≥min_sup×|DB|) then
12) insert L1[i] ∪ L1[j] into L2
13) end if
14) end for
2.2 挖掘频繁k-项集在挖掘频繁k-项集的过程中,首先需要连接两个频繁k-1-项集得到候选k-项集,然后计算候选k-项集的支持度是否符合用户设定的最小支持度要求,进而得到频繁k-项集。由于这种方式连接复杂且会产生很多无用的候选k-项集,BLFPM使用集合枚举树来代表搜索空间,直接遍历集合枚举树便可得到候选k-项集。与此同时,BLFPM利用性质1,使用子集非频繁剪枝策略对集合枚举树进行剪枝操作,大大减小了频繁模式挖掘的搜索空间,提高了算法的执行速度。利用集合枚举树得到候选k-项集之后,BLFPM需要对相应的频繁k-1-项集的B-list进行连接操作,从而得到k-项集的B-list,因此B-list的连接效率会直接影响算法最终的挖掘效率。针对此问题,本节提出了一种高效的B-list连接策略并将其应用到BLFPM中,能大大提高BLFPM算法的效率。
2.2.1 集合枚举树及其剪枝策略集合枚举树是Burdick等[13]于2005年提出来的。利用集合枚举树可以完整地描述所有可能出现的频繁项集。由性质1可知,所有非频繁子集的超集都是非频繁项集,利用此性质可以对集合枚举树进行剪枝操作,从而减小搜索空间,提高算法效率。得到频繁k-项集之后,利用k-项集删除集合枚举树中代表非频繁项集及其超集的节点,可以大大简化集合枚举树。本文例子利用频繁2-项集L2进行剪枝操作后的集合枚举树如图 2所示。从图中可以看出,候选频繁3-项集只有CAB、CAE两项,远远小于由频繁2-项集连接产生的候选3-项集的数量。
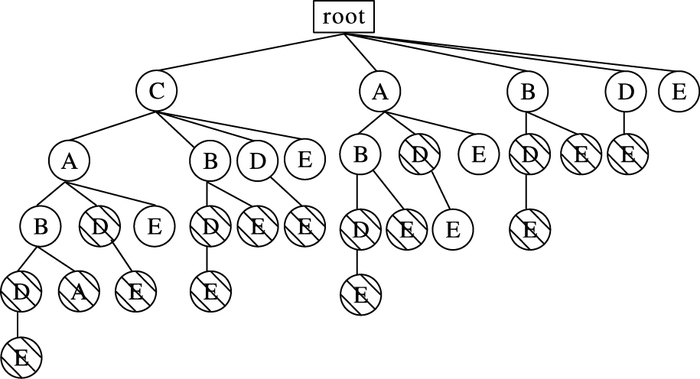
|
图 2 利用L2剪枝后的集合枚举树 Figure 2 Set-enumeration tree pruned by L2 |
连接两个B-list理论上具有O(m×n)复杂度,通过研究发现性质4,可以将其复杂度降为O(m+n)。
性质4 设项集X对应的B-list为{[(s11, f11),c11],[(s12, f12),c12],…,[(s1n, f1n),c1n]}, 项集Y对应的B-list为{[(s21, f21),c21],[(s22, f22),c22],…,[(s2m, f2m),c2m]},如果[(s1i, f1i),c1i](1≤i≤n)是[(s2j, f2j),c2j](1≤j≤m)的祖先,则项集X中其余的B-info-code都不是[(s2j, f2j),c2j]的祖先。
证明 如果[(s1i, f1i),c1i]是[(s2j, f2j),c2j]的祖先,设N1是[(s1i, f1i),c1i]所代表的节点,N2是[(s2j, f2j),c2j]所代表的节点,N为[(s1k, f1k),c1k](k≠i)所代表的节点,易知N1是N2的祖先。假设N为N2的祖先,则N1与N必定存在孩子祖先关系。由于[(s1i, f1i),c1i]与[(s1k, f1k),c1k]均为项集X所对应的B-info-code,因此N1与N所代表节点具有相同的项目名称,由TB-tree的构建算法可知,具有相同项目名称的节点不可能存在孩子祖先关系,因此假设不成立,[(s1k, f1k),c1k]不可能是[(s2j, f2j),c2j]的祖先。证毕。
利用性质4连接两个B-list的方法如下(以性质4中项集X和Y为例)。
1) 首先判断[(s1i, f1i),c1i]与[(s2j, f2j),c2j]之间的祖先-后代关系
2) 如果[(s1i, f1i),c1i]是[(s2j, f2j),c2j]的祖先,则将[(s1i, f1i),c2j]添加到项集XY的B-list中并进行合并操作。如果[(s2j+1, f2j+1),c2j+1]存在,则执行1),判断[(s1i, f1i),c1i]与[(s2j+1, f2j+1),c2j+1]之间的祖先-后代关系;如果[(s2j+1, f2j+1),c2j+1]不存在,则算法结束。
3) 如果[(s1i, f1i),c1i]不是[(s2j, f2j),c2j]的祖先,则存在两种情况,s1i大于s2j或s1i小于s2j。
如果s1i大于s2j,则判断[(s2j+1, f2j+1),c2j+1]是否存在:如果存在则执行1),判断[(s1i, f1i),c1i]与[(s2j+1, f2j+1),c2j+1]之间的祖先-后代关系;如果[(s2j+1, f2j+1),c2j+1]不存在,则算法结束。
如果s1i小于s2j,则判断[(s1i+1, f1i+1),c1i+1]是否存在:如果存在则执行1),判断[(s1i+1, f1i+1),c1i+1]与[(s2j, f2j),c2j]之间的祖先-后代关系; 如果[(s1i+1, f1i+1),c1i+1]不存在,则算法结束。
例如,连接项集A与E的B-list,首先比较[(1,2),1]与[(5,3),1],发现[(1,2),1]不是[(5,3),1]的祖先且1<5,则比较[(6,9),3]与[(5,3),1],比较得知[(6,9),3]不是[(5,3),1]的祖先且6>5,则转向比较[(6,9),3]与[(7,5),1],发现[(6,9),3]是[(7,5),1]的祖先,因此将[(6,9),1]加入项集AE的B-list,继续比较[(6,9),3]与[(9,6),1],发现[(6,9),3]是[(9,6),1]的祖先,因此将[(6,9),1]加入项集AE的B-list,然后对AE的B-list进行合并操作,得到项集AE最终的B-list为[(9,6),2],算法结束。
同prepost算法和NSFI算法相比,BLFPM不需要两次遍历TB-tree来得到B-list,而是在TB-tree的构建过程中完成B-list的构建,节约了两次遍历TB-tree的时间开销;BLFPM利用集合枚举树对候选项集进行剪枝,减少了候选项集的产生,减少了产生大量候选项集的时间与空间开销。由于BLFPM采用的TB-tree结构可以大量压缩稠密数据库的数据量,使其能够快速挖掘稠密数据库中的频繁模式,又因为其采用的剪枝策略,对稀疏数据库进行挖掘也有较高的效率,因此BLFPM不仅适用于稠密数据库,在稀疏数据库中也有良好的表现。
3 实验结果与分析为了验证算法的性能,将本文算法BLFPM与prepost和NSFI算法从运行时间和内存占用两个方面进行对比。实验环境为Intel Core i5 3.1 GHz CPU, 2 GB内存,Windows 7操作系统。所有算法均用Java语言实现,在同一台机器上运行,保证了实验结果的公平性。实验所用数据集为两个常用数据集,分别为Accidents、Retail。实验通过改变最小支持度进行频繁模式挖掘,记录算法运行时间和内存占用情况,其中运行时间实验结果如图 3所示,内存占用实验结果如图 4所示。

|
图 3 运行时间对比 Figure 3 Comparison of runtime |

|
图 4 内存消耗对比 Figure 4 Comparison of memory usage |
在同一数据集条件下,将BLFPM算法的挖掘结果与prepost算法和NSFI算法的挖掘结果进行比较分析,发现在最小支持度相同时,挖掘出的频繁模式的数量和内容完全一致,表明本文算法是正确的。由图 3(a)与图 3(b)可以看出,随着最小支持度的增大,三种算法运行时间都随之降低,但是BLFPM始终比prepost和NSFI运行速度快,表明本文算法具有较高的时间效率。由图 4(a)与图 4(b)可以看出,本文算法的内存消耗始终小于prepost和NSFI,表明本文算法也具有较高的空间效率。造成这种结果的原因是BLFPM建树简单且采用集合枚举树代表搜索空间,同时使用高效的子集非频繁剪枝策略缩小了搜索空间,从而加快了算法执行,减小了内存消耗。理论分析和实验结果表明,BLFPM算法不仅适用于挖掘稠密数据库中的频繁模式,在挖掘稀疏数据库中的频繁模式时也有良好表现。
4 结语本文提出了一种新的频繁模式挖掘算法——BLFPM。该算法使用B-list代表频繁项集,采用集合枚举树与子集非频繁剪枝策略缩减搜索空间,使用高效的B-list连接策略,从而可以快速挖掘出频繁项集。实验结果表明BLFPM算法优于现有效率较高的prepost算法与NSFI算法。在当前大数据环境下,将BLFPM与Hadoop结合,研究出能够并行处理大数据的频繁模式挖掘算法,将会是下一步的研究方向。
| [1] | AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules[C]//VLDB 1994:Proceedings of the 20th VLDB International Conference on Very Large Data Bases. San Francisco, CA:Morgan Kaufmann Publishers Inc., 1994:487-499. |
| [2] | SAHOO J, DAS KUMAR A, GOSWAMI A. An efficient approach for mining association rules from high utility itemsets[J]. Expert Systems with Applications, 2015, 42(13): 5754-5778. DOI:10.1016/j.eswa.2015.02.051 |
| [3] | CAMPAGNA A, PAGH R. Finding associations and computing similarity via biased pair sampling [C]// ICDM' 09: Proceedings of the 2009 Ninth IEEE International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2009: 61-70. |
| [4] | ATTEYA W A, DAHAL K, HOSSAIN M A. Distributed BitTable multi-Agent association rules mining algorithm [C]// KES' 11: Proceedins of the 15th International Conference on Knowledge-Based and Intelligent Information and Engineering Systems, LNCS 6881. Berlin: Springer-Verlag, 2011: 151-160. |
| [5] | 赵学健, 孙知信, 袁源, 等. 一种正交链表存储的改进Apriori算法[J]. 小型微型计算机系统, 2016, 37(10): 2291-2295. (ZHAO X J, SUN Z X, YUAN Y, et al. An improved apriori algorithm based on orthogonal storage[J]. Journal of Chinese Computer Systems, 2016, 37(10): 2291-2295.) |
| [6] | HAN J, PEI J, YIN Y. Mining frequent patterns without candidate generation[J]. ACM SIGMOD Record, 2000, 29(2): 1-12. DOI:10.1145/335191 |
| [7] | 李也白, 唐辉, 张淳, 等. 基于改进的FP-tree的频繁模式挖掘算法[J]. 计算机应用, 2011, 31(1): 101-103. (LI Y B, TANG H, ZHANG C, et al. Frequent pattern mining algorithm based on improved FP-tree[J]. Journal of Computer Applications, 2011, 31(1): 101-103.) |
| [8] | MA Z, YANG J, ZHANG T, et al. An improved eclat algorithm for mining association rules based on increased search strategy[J]. International Journal of Database Theory and Application, 2016, 9(5): 251-266. DOI:10.14257/ijdta |
| [9] | DENG Z, WANG Z, JIANG J. A new algorithm for fast mining frequent itemsets using N-lists[J]. SCIENCE CHINA Information Sciences, 2012, 55(9): 2008-2030. DOI:10.1007/s11432-012-4638-z |
| [10] | VO B, LE T, COENEN F, et al. Mining frequent itemsets using the N-list and subsume concepts[J]. International Journal of Machine Learning and Cybernetics, 2016, 7(2): 253-265. DOI:10.1007/s13042-014-0252-2 |
| [11] | DAM T-L, LI K, FOURNIER-VIGER P, et al. An efficient algorithm for mining top-rank-k frequent patterns[J]. Applied Intelligence, 2016, 45(1): 96-111. DOI:10.1007/s10489-015-0748-9 |
| [12] | MOHAMED M H, DARWIEESH M M. Efficient mining frequent itemsets algorithms[J]. International Journal of Machine Learning and Cybernetics, 2014, 5(6): 823-833. DOI:10.1007/s13042-013-0172-6 |
| [13] | BURDICK D, CALIMLIM M, FLANNICK J, et al. MAFIA: a maximal frequent itemset algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(11): 1490-1504. DOI:10.1109/TKDE.2005.183 |




