根据长期演进(Long Term Evolution,LTE)标准和第五代移动通信技术(5th-Generation, 5G)预期,未来的蜂窝网将会是异构密集网络[1]。异构网络是宏基站和微基站、微微基站、家庭基站以及中继等组成的混合网络。各类小基站可以提升频谱复用和覆盖性能,并提供高速率业务和无缝连接[2]。
随着基站密度的增加,网络能源消耗不断增加,并成为温室气体排放过多的重要原因之一。绿色通信也因此引起关注[3],其主要目标是在满足用户需求条件下尽可能提升能效,同时也能降低成本投入并延长移动设备待机时间。移动蜂窝网中基站耗能占60%~80%[4]。由于小基站比宏基站功率低得多,因此更利于提升能效和降低网络运维支出。本文拟研究在已部署宏基站区域部署微基站的能效问题,在满足不断增加的业务需求同时限制增加的微基站数量。
异构网络中已有研究主要集中在功率控制和资源分配方面[5-8],微基站部署和能效方面研究相对较少。文献[9-10]考虑在宏基站覆盖区域中部署微基站以提升区域的频谱效率。为通过扩大基站覆盖范围提升频效,文献[9]选择小区边界作为部署微基站的候选位置,并采用贪婪算法确定位置;文献[10]则利用一种基于随机几何和蒙特卡洛仿真的微基站自动部署方法来确定微基站位置;文献[11]将微基站部署问题分解为簇形成子问题和资源管理子问题,以服务的用户数最大化为目标提出了迭代的实时微基站部署算法。但是上述几种方案均不是从能效方面考虑,如果从能效方面考虑的话,上述方案确定的微基站部署位置可能不是优选位置,特别是在用户聚集在宏基站附近的场景下,文献[9]提出的算法表现不佳。
文献[12]在满足频效和覆盖等约束下,通过优化微基站数目和调整功率来提升系统的能效;文献[4]基于能效研究了异构网络部署和资源管理问题,求解了微基站最优密度和功率。但是这两者均未能确定微基站的具体部署位置。文献[13]首先选择可行位置子集作为微基站候选位置,然后在这些候选位置中选择最优的子集来优化网络能效,但是它没有考虑功率对优化目标的影响。由于微基站发射功率对网络能效有较大影响,在以能效为优化目标并确定微基站位置的部署方案中应当考虑功率因素。
本文从能效方面考虑微基站的部署问题。针对边界位置未必是最优的问题,考虑在所有可行的位置部署微基站;针对不同用户状态影响系统能效的问题,考虑在不同的用户分布状态下对优化目标依概率进行加权,增强方法对不同用户分布状态的适应性;考虑功率对能效的影响,给出微基站位置、数量和功率确定的高能效异构网络部署方案。
1 系统模型一般而言,移动通信系统中的能效度量准则可以分为三大类:元件级、设备级和网络级。本文考虑的是网络级能效,常用准则为能量消耗比率(Energy Consumption Rating, ECR),定义为系统功率损耗与系统有效吞吐量的比值,单位为W/(b·s-1)。为使其更直观,选用较常用的ECR的倒数形式[13],即系统有效吞吐量与系统功率损耗的比值,单位为b/J。下面将分别给出吞吐量分析和功耗模型,进而表示出网络能效。
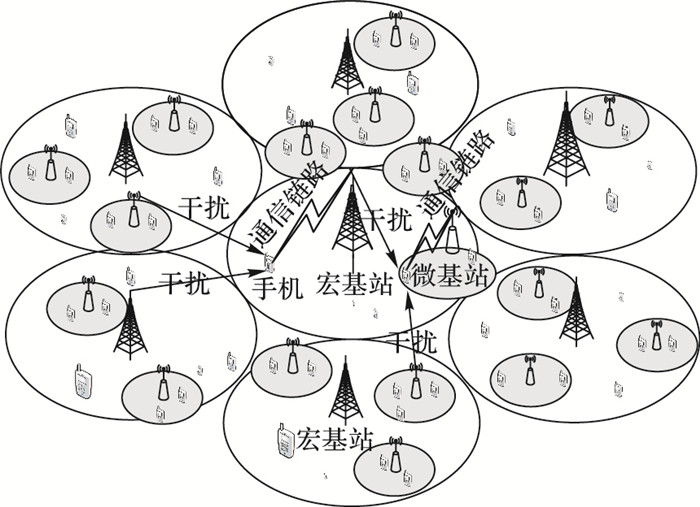
1.1 用户吞吐量模型本文考虑图 1所示的由宏基站和微基站组成的两层异构无线网络,用户终端与接收信号信干噪比(Signal to Interference plus Noise Ratio, SINR)最大的基站连接进行通信,即采用基于SINR的关联。为了尽量提高频谱利用率,宏基站与微基站共享同一段频谱。因此,宏基站与微基站间存在层间干扰,而微基站间因使用相同的频率资源而存在层内干扰。
|
图 1 两层异构无线网络模型示意图 Figure 1 Schematic diagram of two-tier heterogeneous wireless network model |
与LTE系统相同,基站频率资源由若干等带宽的子载波组成,并以包含若干子载波的资源块为频率资源分配的最小粒度。假设活跃的移动用户一直传输数据,因此需要分配带宽,同时假设同类型基站使用相同的发送功率,并平均分配功率至各子载波。宏基站和微基站用各自位置集合BM和Bm表示(下标M和m表示宏基站和微基站)。BM和Bm分别包含宏基站和微基站的位置坐标。网络中所有基站用B=BM∪Bm表示。则与宏基站子载波n相关联的用户k的SINR[13]可以表示为:
| $ \gamma _{kM}^{(n)} = \frac{{P_M^{(\mathit{n})}{g_{k,b}}}}{{\sum\limits_{{b^\prime } \in {\mathit{\boldsymbol{B}}_M},{b^\prime } \ne b} {P_M^{(\mathit{n})}{g_{k,{b^\prime }}}} + \sum\limits_{{b^\prime } \in {\mathit{\boldsymbol{B}}_m}} {P_m^{(\mathit{n})}{g_{k,{b^\prime }}}} + {\sigma ^2}}} $ | (1) |
其中:PM(n)和Pm(n)分别是宏基站M和微基站m在子载波n上的传输功率; gk, b指的是基站b和用户k之间的信道增益,包括路径损耗、阴影衰落和多径衰落等。由于微基站部署和信道测量时间相对较长,所以可通过平均法消除快衰落对信道影响,信道增益主要考虑路径损耗。σ2表示的是单个子载波上的热噪声。类似地,与微基站子载波n相关联的用户k的SINR可以表示为:
| $ \gamma _{km}^{\rm{(}\mathit{n}\rm{)}}=\frac{P_{m}^{\rm{(}\mathit{n}\rm{)}}{{g}_{k, b}}}{\sum\limits_{{{b}^{\prime }}\in {{\mathit{\boldsymbol{B}}}_{m}}, {{b}^{\prime }}\ne b}{P_{m}^{\rm{(}\mathit{n}\rm{)}}{{g}_{k, {{b}^{\prime }}}}}+\sum\limits_{{{b}^{\prime }}\in {{\mathit{\boldsymbol{B}}}_{M}}}{P_{M}^{\rm{(}\mathit{n}\rm{)}}{{g}_{k, {{b}^{\prime }}}}}+{{\sigma }^{2}}} $ | (2) |
为简单起见,本文统一用γk(n)来表示宏基站和微基站用户的信干噪比,那么用户k的吞吐量(单位:b/s)可以表示为:
| $ C(k, \mathit{\boldsymbol{B}})=\sum\limits_{n=1}^{{{N}_{k}}}{W_{k}^{\rm{(}\mathit{n}\rm{)}}\rm{lb}}\rm{(}1+\gamma _{\mathit{k}}^{\rm{(}\mathit{n}\rm{)}}\rm{) } $ | (3) |
其中:Wk(n)表示分配给用户k的子载波n的带宽,Nk表示分配给用户k的子载波数。此处采用等带宽分配,即每个基站将带宽资源平均分配至关联的用户。
1.2 功耗模型及网络能效基站的功耗包括两部分。一部分是基站没有传输时也会消耗的静态功率,另一部分是基于负载和基站的发送功率。本文采用文献[14]提出的功耗模型:
| $ P=\beta {{P}_{\rm{t}}}+{{P}_{\rm{c}}}\rm{ } $ | (4) |
其中:P表示基站功耗,Pt表示发送功率,β表示对基于负载的发送功率的加权系数,Pc表示基站的静态功耗。
如前所述,假设用户总有数据传输。此外基站不采用功率控制算法,即基站服务用户时Pt为常数,那么网络能效可以表示为:
| $ EE\rm{(}\mathit{\boldsymbol{B}}\rm{)}=\frac{\sum\limits_{\mathit{k}\in \mathit{\boldsymbol{K}}}{\mathit{C}\rm{(}\mathit{k}, \mathit{\boldsymbol{B}}\rm{)}}}{{{\mathit{N}}_{\rm{B}}}\cdot {{\mathit{P}}_{\mathit{M}}}+{{\mathit{N}}_{\rm{b}}}\cdot {{\mathit{P}}_{\mathit{m}}}} $ | (5) |
其中:NB和Nb分别表示网络中宏基站和微基站数目,PM和Pm分别表示网络中宏基站和微基站的功耗,K表示网络中的用户集合。
网络能效可以通过在功率相同时增大网络吞吐量或在保持容量不变时减小消耗的功率两种方法提升。在密集网络中,由于微基站的传输距离短,因此传输功率要远低于宏基站,与其他微基站的干扰也比宏基站传输的干扰低,并且通信速率也相对较高。鉴于以上原因,微基站被用来叠加在宏基站覆盖范围内以满足用户的业务需求,并使网络能效最大化。
2 微基站部署策略本章提出了一种高能效的满足覆盖需求的微基站部署策略:首先,给出了宏基站和微基站的覆盖需求并形成微基站部署的优化问题;然后,在此基础上给出微基站的具体部署算法。
2.1 宏基站和微基站的覆盖需求网络运营商希望通过增加微基站提高网络吞吐量以满足不断增长的业务需求。为了使网络能效最大化,降低资本支出和运维支出,网络运营商需要将微基站部署在最优位置以满足用户服务质量(Quality of Service, QoS)需求。覆盖性能是移动通信一个重要的QoS指标,通常由小区边缘用户SINR大于某一阈值来测定。但是,SINR并不能保证用户的数据速率,所以本文采用速率覆盖[15],即用户的速率大于某一阈值或大于需求速率。在现实场景中,用户不断移动,不同的用户分布以不同概率出现,部署的微基站需要满足不同用户分布状态下的用户速率覆盖需求。
假设R表示用户状态分布的集合,r∈R指的是某种用户状态分布,即对应于某种用户分布场景,πr表示分布场景r的发生概率。用Kr表示分布场景r中用户的集合,Cr(k, B)表示Kr中用户k的吞吐量,C表示用户速率的阈值。另外,在分布场景r下的网络能效用EEr(B)表示,即:
| $ E{{E}_{r}}\rm{(}\mathit{\boldsymbol{B}}\rm{)}=\frac{\sum\limits_{\mathit{k}\in {{\mathit{\boldsymbol{K}}}_{\mathit{r}}}}{{{\mathit{C}}_{\mathit{r}}}\rm{(}\mathit{k}, \mathit{\boldsymbol{B}}\rm{)}}}{{{\mathit{N}}_{\rm{B}}}\cdot {{\mathit{P}}_{\mathit{M}}}+{{\mathit{N}}_{\rm{b}}}\cdot {{\mathit{P}}_{\mathit{m}}}} $ | (6) |
因此,优化问题可以表示为
| $ \begin{array}{l} \;\;\;\mathop {{\rm{max}}}\limits_{{\mathit{P}_{{\rm{tm}}}}, \mathit{\boldsymbol{B}}} \eta {\rm{(}}\mathit{\boldsymbol{B}}{\rm{)}} = \sum\limits_{\mathit{r} \in \mathit{\boldsymbol{R}}} {{\pi _r}} E{E_r}{\rm{(}}\mathit{\boldsymbol{B}}{\rm{)}}\\ {\rm{s}}.{\rm{t}}.\;\;\;\;{C_r}{\rm{(}}k, \mathit{\boldsymbol{B}}{\rm{)}} \ge C{\rm{ }}\\ \;\;\;\;\;\;\;\;\;{\rm{ }}\forall r \in \mathit{\boldsymbol{R}}, \forall k \in {\mathit{\boldsymbol{K}}_{r }} \end{array} $ | (7) |
其中:Ptm为微基站的发送功率; Cr(k, B)和Pm分别为Ptm对应条件下用户k的吞吐量和单个微基站总功耗。
2.2 微基站部署算法本文修改文献[11]中的随机搜索算法以及文献[9, 13]中的贪婪算法给出新的微基站部署算法。其中文献[13]方法的过程如下:首先在观察区域划分网格对微基站的可行位置集合进行筛选产生候选位置集合,然后运用贪婪算法,每次从候选位置选择使网络能效最大的位置部署微基站,下次选择时均以之前选择的位置已部署微基站为前提,这样逐一增加微基站直至网络吞吐量的提升倍数达到阈值要求。
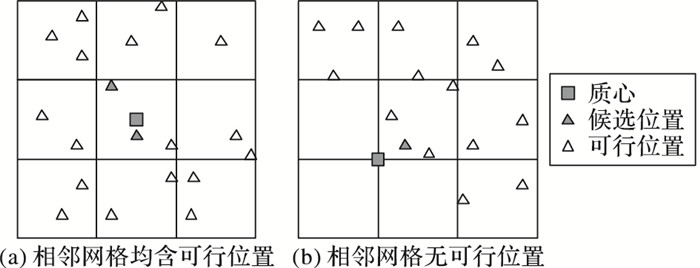
筛选可行位置时,网络区域分为若干相同的网格,从且仅从包含可行位置的每个网格选出一个候选位置。当网格与其近邻均至少有一个可行位置时,则选离该网格质心最近的可行位置为候选位置;而当网格有不含可行位置的近邻时,则选离该网格和其所有不含可行位置的近邻共同的质心最近的可行位置作为候选位置。图 2为选择候选位置的一个场景。
|
图 2 选择候选位置过程 Figure 2 Process of selecting the candidate location |
上述微基站部署方法虽然有效避免了可行位置过多和遍历所有可能方案带来的计算量过大问题,但是网络总吞吐量提升不能保证单个用户的QoS;同时算法在进行增量部署时也未考虑已部署微基站的冗余问题。为保证每个用户的QoS并解决已部署微基站冗余问题,本文首先对文献[13]中的贪婪算法进行改进得到算法1中的固定功率部署算法(Fixed Power Deployment Algorithm, FPDA)。FPDA除将需求由网络吞吐量提升改为每个用户吞吐量均大于阈值,覆盖约束条件更加严格,还在部署每个微基站时去除冗余的微基站。伪代码中,C表示用户吞吐量阈值,Ptm表示微基站发送功率,Bm为求解的部署微基站的位置集合,Bm_idle为部署时产生的冗余微基站位置集合,Nc表示候选位置数量,Bc表示候选位置的坐标集合,argmax表示选择式(7) 中的优化目标改变最大的微基站,最终输出Bm和η(Ptm, Bm)作为部署微基站位置集的优化解和对应的优化目标值。算法中能效和用户吞吐量对应所有部署基站位置集合,因为宏基站位置集合保持不变,为便于理解和叙述方便,计算能效和吞吐量的参数B简化表示成Bm。
算法1 FPDA。
1) 初始化:C, Ptm, Nc, n=0, η=0, Bc, Bm=∅, BM, K, R
2) Function FPDA(C, Ptm, Nc, Bc, BM, K, R)
3) While Cr(k, B) < C, ∀r∈R, ∀k∈Kr & Bc≠∅ & n < Nc do
4)
5) Bm=Bm∪b\Bm_idle
6) Bc=Bc\b∪Bm_idle
7) n=n+1
8) End while
9) Return η(Ptm, Bm), Bm
10) End function
文献[13]还未考虑功率对网络能效的影响,单一的功率设置限制了能效的提升。基于此,并修改文献[11]中的基于模拟退火的随机搜索算法,本文提出了联合优化微基站数量、位置和功率的高能效部署算法(High Energy Efficient Deployment Algorithm, HEEDA),优化步骤可描述如下:
步骤1 给定微基站发射功率优化微基站数量和位置。应用FPDA根据输入条件依次选择使式(7) 中的优化目标最大的位置部署微基站,该过程重复直至满足所有场景的速率覆盖需求。
步骤2 基于上述优化的微基站数量和位置进行功率优化。根据输入条件和上述优化的微基站数量和位置,进一步对发射功率进行微调来最大化式(7) 中的优化目标,从而得到新的微基站发射功率、位置和数量配置信息,由细粒度功率调整算法(FGAPA)实现。
步骤3 粗调上述优化的微基站发射功率并迭代寻优。在设定复杂度要求下利用随机搜索算法更新当前解,并粗粒度调整功率重复前两步迭代搜索,既有效避免了贪婪算法陷入局部最优,也可通过调整算法的迭代次数实现优化度和复杂度之间的折中。
事实上HEEDA由算法2中的伪代码给出,其中ΔP1和ΔP2分别表示粗粒度和细粒度调整Ptm的步长,Ptm_t和Bm_t为求解过程中的当前解,Ptm和Bm则为近邻解,t和θ依次表示冷却温度和冷却比,I和Imax则为求解次数及其上限,最终输出(ηapprox, Ptm_approx, Bmapprox)作为能效、微基站功率和部署位置集的近优解。
算法2 HEEDA。
1) 初始化:C, Ptm, Ptm_t, Ptm_min, Ptm_max, ΔP1, ΔP2, t, θ, Imax, I=0, ηapprox=0, Ptm_approx=0, BM, Bc, K, R, Bm=∅, Bm_t=∅, Bmapprox=∅
2) Function HEEDA(C, Ptm, Ptm_t, Ptm_min, Ptm_max, ΔP1, ΔP2, t, θ, I, Imax, Bm_t, BM, Bc, K, R) //第一步:给定微基站发射功率优化微基站数量和位置
3) (η(Ptm, Bm), Bm)←FPDA(C, Ptm, Nc, Bc, BM, K, R) //第二步:基于上述优化的微基站数量和位置进行功率//优化
4) (Ptm, Bm)←FGAPA(C, Ptm, Ptm_min, Ptm_max, ΔP1, ΔP2, Bm, BM, Bc, K, R) //第三步:粗调上述优化的微基站发射功率迭代寻优
5) While I < Imax do
6) dη=η(Ptm, Bm)-η(Ptm_t, Bm_t)
7) If dη > 0
8) If η(Ptm, Bm) > η(Ptm_approx, Bmapprox)
9) ηapprox=η(Ptm, Bm), Ptm_approx=Ptm, Bmapprox=Bm
10) End if
11) Ptm_t=Ptm, Bm_t=Bm
12) Else
13) Ptm_t=Ptm且Bm_t=Bm with Probability edη/t
14) End if
15) Ptm=(Ptm+ΔP1) mod Ptm_max
16) If Ptm < Ptm_min
17) Ptm=(Ptm+ΔP1) mod Ptm_max
18) End if
19) I=I+1, t=θt
20) go to 3)
21) End while
22) return ηapprox, Ptm_approx, Bmapprox
23) End function
下面的算法3给出了中间算法FGAPA(Fine Grained Power Adjustment Algorithm)的详细过程,其中Pul和Pll分别表示细粒度调整功率的上限和下限,两者均由输入微基站功率和粗调功率的步长确定,最终算法输出微调后的微基站功率Ptm和对应微基站位置集合Bm。
算法3 FGAPA。
1) 初始化:C, Ptm, Ptm_min, Ptm_max, ΔP1, ΔP2, Bm, BM, Bc, K, R
2) Function FGAPA(C, Ptm, Ptm_min, Ptm_max, ΔP1, ΔP2, Bm, BM, Bc, K, R)
3) Ptm_0=Ptm_1=Ptm, Bm0=Bm1=Bm
4) Pul=min(Ptm_max, Ptm+ΔP1/2), Pll=max(Ptm_min, Ptm-ΔP1/2)
5) While Ptm_0+ΔP2≤Pul & Cr(k, Bm0\Bm_idle)≥C, ∀r∈R, ∀k∈Kr do
6) If η(Ptm, Bm) < η(Ptm_0+ΔP2, Bm0\Bm_idle)
7) Ptm=Ptm_0+ΔP2, Bm=Bm0\Bm_idle
8) End if
9) Ptm_0=Ptm_0+ΔP2, Bm0=Bm0\Bm_idle
10) End while
11) While Ptm_1-ΔP2≥Pll & Cr(k, Bm1\Bm_idle)≥C, ∀r∈R, ∀k∈Kr do
12) If η(Ptm, Bm) < η(Ptm_1-ΔP2, Bm1\Bm_idle)
13) Ptm=Ptm_1+ΔP2, Bm=Bm1\Bm_idle
14) End if
15) Ptm_1=Ptm_1-ΔP2, Bm1=Bm1\Bm_idle
16) End while
17) return Ptm, Bm
18) End function
当微基站功率Ptm一定时,因为第一步中的FPDA是贪婪的启发式算法,所以不能保证获得的解是最优解。然而文献[16]提出如果贪婪算法满足:1)η(∅)=0;2)η不单调递减; 3)η是子模的,那么算法求得的解对应的能效ηapprox(Ptm)至少为最优解对应能效ηopt(Ptm)的(e-1)/e倍,记为η*(Ptm)=(e-1)/e×ηopt(Ptm),其中e为自然常数。虽然能效函数η可能单调递减,但是文献[9]指出区域频谱效率(Area Spectral Efficiency, ASE)满足以上三个条件。ASE定义为某个区域的总吞吐量比带宽,因此对于特定区域和带宽可以说总吞吐量也满足以上条件和关系。如果假设最优解和所提算法求得的解对应的部署微基站数量相等,即两者能耗相等,那么求得的解对应能效即总吞吐量比能耗至少为η*。考虑功率对能效影响,在变化区间内调整微基站功率时,对于每个功率取值,上述关系仍然存在。如果调整功率步长设置足够小并假设迭代中调整功率时能够取得最优功率值Ptm_opt,那么此时求得的解对应能效ηapprox(Ptm_opt)也能达到η*(Ptm_opt)。此外,由于算法中去除了冗余的微基站,所以求得的解较一般贪婪算法更趋近于最优解。
3 仿真分析以下将对本文提出的部署算法与文献[13]中的方法进行比较。
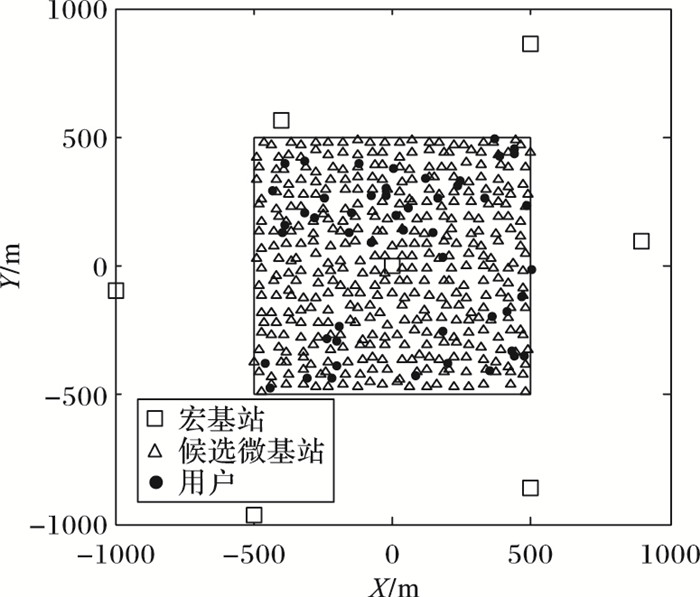
3.1 仿真场景已部署宏基站,以及候选微基站集合和用户分布如图 3所示,7个宏基站部署在2 km×2 km仿真区域。为避免边界效应,采集中央1 km×1 km区域的数据。用户在宏基站小区内可以为任意分布,假设5个服从随机分布的不同用户分布场景依相同概率出现,当然其他任意分布场景本文方法仍然适用。为刻画现实情况中宏基站位置的随机性,宏基站位置由齐次泊松点过程(homogeneous Poisson Point Process, PPP)模型产生。为刻画微基站可行位置间的不相关性,可行位置由参数λ为2 000的PPP模型生成。仿真模型和参数如表 1所示[17]。假设宏基站使用三扇区天线,微基站则为全向天线。综合考虑算法的复杂度与性能以及观察区域面积,筛选可行位置的网格数选为400。优化中,Ptm和ΔP1以及ΔP2分别设为1 W、0.3 W和0.002 W,t=1,θ=0.99,Imax=2 000。
|
图 3 仿真场景 Figure 3 Simulation scenario |
| 表 1 仿真参数 Table 1 Simulation parameters |
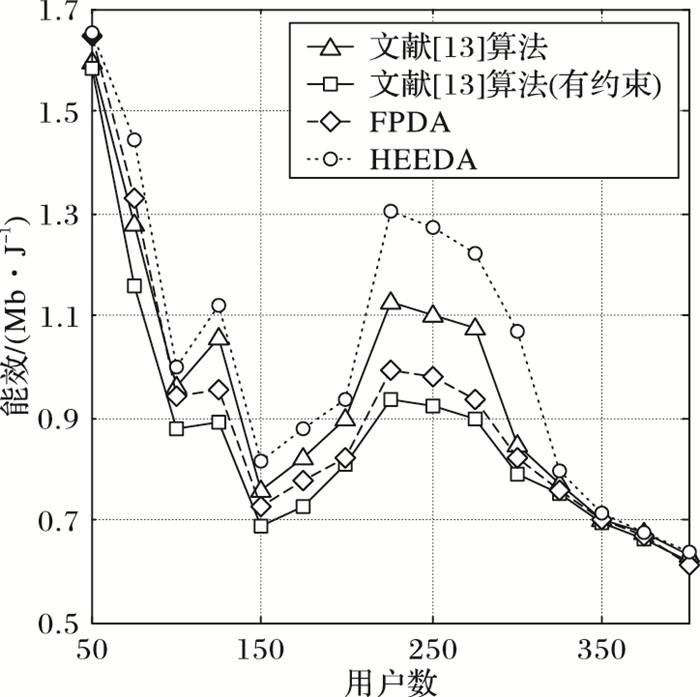
图 4比较了本文提出的FPDA和HEEDA以及作为参考算法的文献[13]中算法的性能,同时还给出了参考算法仅修改约束条件为单用户吞吐量达到阈值后的性能曲线。为增强可比性,参考算法的网络吞吐量提升要求设为HEEDA求得解对应的网络吞吐量提升倍数。此处主要比较了能效的增益。各算法均从没有微基站开始,随着用户数的增加,部署微基站数量逐渐增加。随着微基站数量增加,网络总吞吐量绝对值单调递增,但是能效曲线却曲折变化并升至最高点后呈总体下降趋势。对于图中任意一个用户数位置,在能效方面,本文所提算法均明显优于参考算法性能,在用户数为300附近,HEEDA相对参考算法能效提升接近26%,达到最大,网络能效在峰值处提升达12%。从图中还可以看出FPDA和增加单用户速率约束的参考算法在能效方面普遍低于参考算法,这是因为两者均增加了速率覆盖要求,所以能效水平提升受到一定限制;但是由于考虑了冗余微基站问题,FPDA能效方面均优于修改约束的参考算法。
|
图 4 几种算法能效性能曲线比较 Figure 4 Energy efficiency performance curves of different algorithms |
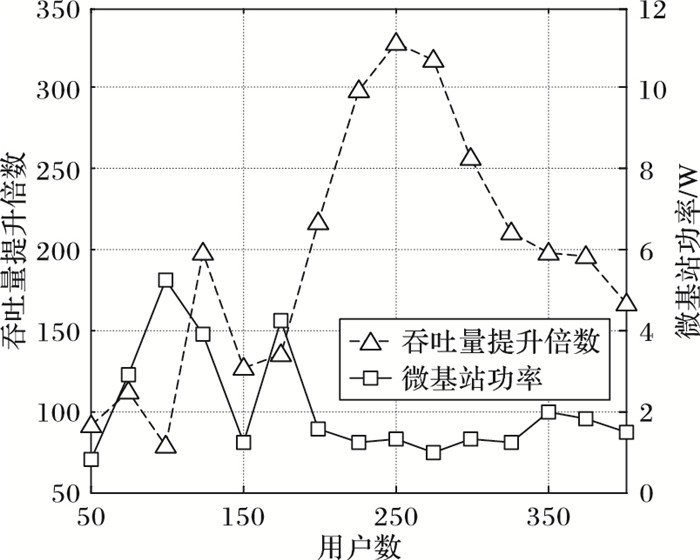
图 5给出了HEEDA在不同用户数条件下部署微基站时的网络吞吐量提升倍数和微基站发送功率。吞吐量提升倍数为部署微基站后的网络吞吐量与部署前仅有宏基站时的吞吐量之比。对于网络吞吐量,尽管其绝对值随着用户数和部署基站数增加会单调上升,但由图 6可知其相对值在用户数较少时呈总体上升趋势,达到峰值后又迅速下降。这主要是由于用户数和微基站数量的增加使干扰不断增强,继续增加微基站带来的吞吐量提升越来越有限。
|
图 5 HEEDA吞吐量提升倍数与微基站功率 Figure 5 Throughput improvement and micro base station power of HEEDA |
|
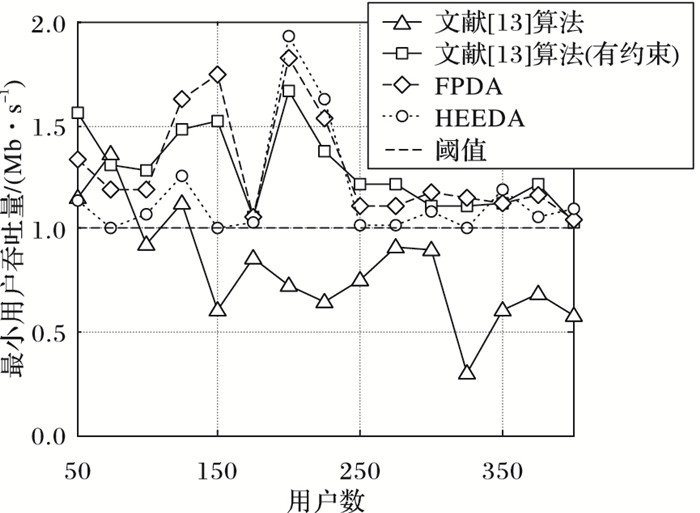
图 6 几种算法用户最小吞吐量比较 Figure 6 Minimum user throughput of different algorithms |
对于微基站功率,容易看出在用户数少于200时,其变化范围较大;当用户数较大时,微基站功率大小均在0~2 W变化。又由图 4知用户数少于300时能效提升比例较大,可见通过优化功率提升能效作用明显;当用户数较大时,能效提升相对较小,因为求得的微基站功率与初始功率即参考方法中的微基站功率接近,所以HEEDA较参考算法的能效提升主要由迭代搜索优化微基站的位置和数量来实现。因为当干扰成为影响能效提升的主要因素时,较低的微基站功率更利于降低干扰从而提升能效,所以用户数较多时,微基站均取低于2 W的较小功率值。
各算法的用户最小吞吐量随用户数量的变化曲线如图 6所示。容易看出,HEEDA的用户最小吞吐量尽管大多低于修改约束后的参考方法,但是均大于阈值并在阈值曲线以上附近变化。因为没有单用户吞吐量约束,当用户数超过100后,参考算法的最小用户吞吐量均低于HEEDA的用户吞吐量阈值,即不满足速率覆盖需求。此外,对比图 4和图 6,容易得出尽管在用户数多于325时HEEDA与参考方法的能效相差不大,但是用户的最低吞吐量相差较大,所以HEEDA在保证用户QoS方面优于参考方法。
4 结语本文提出了一种联合优化微基站数量、位置和功率的高能效微基站部署方法。部署方法通过对部署位置的有效筛选降低了问题复杂度,利用概率加权适应用户分布的动态变化,并采用基于模拟退火的算法求解从而避免陷入局部最优。联合优化方法在能效方面较仅优化微基站数量和位置的方法有明显提升。为进一步提升系统能效,微基站部署后基于动态业务负载的微基站休眠方法有待后续深入研究。
| [1] | IMT-2020(5G)推进组. 5G无线技术架构白皮书[EB/OL]. (2015-05-29)[2016-11-26]. http://www.imt-2020.org.cn/zh. (IMT-2020(5G) Promotion Group. 5G wireless technology architecture whiter paper[EB/OL]. (2015-05-29)[2016-11-26]. http://www.imt-2020.org.cn/zh.) |
| [2] | NAEEM B, NGAH R, HASHIM S Z M. Handovers in small cell based heterogeneous networks[C]//Proceedings of the 2016 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube). Piscataway, NJ:IEEE, 2016:268-271. |
| [3] | GHAZZAI H, KADRI A. Joint demand-side management in smart grid for green collaborative mobile operators under dynamic pricing and fairness setup[J]. IEEE Transactions on Green Communications and Networking, 2017, 1(1): 74-88. DOI:10.1109/TGCN.2016.2646818 |
| [4] | 彭金磷. 基于能效的异构蜂窝网络部署和资源管理优化[D]. 合肥: 中国科学技术大学, 2015: 35-39. (PENG J L. Energy-efficient network deployment and resource management in heterogeneous cellular networks[D]. Hefei:University of Science and Technology of China, 2015:35-39) |
| [5] | TAM H H M, TUAN H D, NGO D T, et al. Joint load balancing and interference management for small-cell heterogeneous networks with limited backhaul capacity[J]. IEEE Transactions on Wireless Communications, 2017, 16(2): 872-884. DOI:10.1109/TWC.2016.2633262 |
| [6] | KANEKO M, NAKANO T, HAYASHI K, et al. Distributed resource allocation with local CSI overhearing and scheduling prediction for OFDMA heterogeneous networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1186-1199. DOI:10.1109/TVT.2016.2555840 |
| [7] | MLIKA Z, GOONEWARDENA M, AJIB W, et al. User-base-station association in HetSNets:complexity and efficient algorithms[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 1484-1495. DOI:10.1109/TVT.2016.2558501 |
| [8] | 冀保峰, 杨佳, 王一丹, 等. 基于能效最优准则的双跳中继网络功率分配算法[J]. 通信学报, 2016, 37(7): 124-131. (JI B F, YANG J, WANG Y D, et al. Power allocation algorithms in two-hop relaying networks based on optimal energy efficiency[J]. Journal on Communications, 2016, 37(7): 124-131.) |
| [9] | SON K, OH E, KRISHNAMACHARI B. Energy-aware hierarchical cell configuration:from deployment to operation[C]//INFOCOM WKSHPS' 11:Proceedings of the 2011 IEEE Conference on Computer Communications Workshops. Piscataway, NJ:IEEE, 2011:289-294. |
| [10] | GUO W, WANG S, CHU X, et al. Automated small-cell deployment for heterogeneous cellular networks[J]. IEEE Communications Magazine, 2013, 51(5): 46-53. DOI:10.1109/MCOM.2013.6515046 |
| [11] | HSIEH H-Y, WEI S-E, CHIEN C-P. Optimizing small cell deployment in arbitrary wireless networks with minimum service rate constraints[J]. IEEE Transactions on Mobile Computing, 2014, 13(8): 1801-1815. DOI:10.1109/TMC.2013.135 |
| [12] | REN Q, FAN J, LUO X, et al. Energy efficient base station deployment scheme in heterogeneous cellular network[C]//VTC'15:Proceedings of the 2015 IEEE 81st Vehicular Technology Conference. Piscataway, NJ:IEEE, 2015:1-5. |
| [13] | COSKUN C C, AYANOGLU E. A greedy algorithm for energy-efficient base station deployment in heterogeneous networks[C]//ICC'15:Proceedings of the 2015 IEEE International Conference on Communications. Piscataway, NJ:IEEE, 2015:7-12. |
| [14] | ZHENG J, CAI Y, CHEN X, et al. Optimal base station sleeping in green cellular networks:a distributed cooperative framework based on game theory[J]. IEEE Transactions on Wireless Communications, 2015, 14(8): 4391-4406. DOI:10.1109/TWC.2015.2420233 |
| [15] | SINGH S, DHILLON H S, ANDREWS J G. Offloading in heterogeneous networks:modeling, analysis, and design insights[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 2484-2497. DOI:10.1109/TWC.2013.040413.121174 |
| [16] | NEMHAUSER G L, WOLSEY L A, FISHER M L. An analysis of approximations for maximizing submodular set functions-Ⅰ[J]. Mathematical Programming, 1978, 14(1): 265-294. DOI:10.1007/BF01588971 |
| [17] | 3GPP. Evolved Universal Terrestrial Radio Access (E-UTRA), further advancements for E-UTRA:physical layer aspects (Release 9), TR 36.814 v9.0.0[R/OL]. (2010-03-20)[2016-11-26]. https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=2493. |




