在无人车自主跟随系统中,目标车辆检测是跟随车辆自主控制的基础和前提。激光雷达(Light Detection And Ranging, LiDAR)和摄像机是车辆检测常用的两种传感器,Zhao等[1]利用激光雷达分割算法探测目标和确定目标所处位置,同时对相机采集到的图像进行分类,最终通过逻辑模糊算法对两个传感器分别处理后的信息进行融合,对车辆行驶环境进行场景理解。Tan等[2]先将激光雷达扫描点与摄像机图像融合为深度图像,然后根据深度图像中路缘平面的法向方向对路缘进行检测。关超华[3]利用激光雷达和摄像机进行融合对道路上行驶的车辆进行检测,利用激光雷达确定车辆的初始位置,然后利用车辆的Harr-like矩形特征对车辆进行AdaBoost分类识别。为减少目标检测系统的处理时间和提高系统的实时性,融合激光雷达数据和摄像机信息成为当前阶段研究的热点[4]。
激光雷达和摄像机是两种不同类型的传感器,融合激光雷达数据和摄像机图像前需要对激光雷达和摄像机进行标定,即建立传感器坐标之间的变换关系,实现两者的空间配准。激光雷达的标定方法主要包括立体标定法[5-6]和平面模板标定法[7],摄像机的标定方法经过多年的发展逐渐成熟。Zhang等[8]较早研究了基于棋盘格平面板的摄像机和单线激光雷达的标定方法,其标定方法利用激光雷达扫描点位于棋盘格标定平面上的约束关系,实现了激光雷达和摄像机外参数的标定,但激光雷达在平面板上的扫描点是一条直线,3个扫描点是线性相关的,所以此方法要求至少采集5次标定板的数据,才能实现标定。Pereira等[9]利用寻找球体中心位置变换得到激光雷达和摄像机的转换关系,但该方法寻找球体质心算法较复杂。彭梦等[10]设计了一套双平行的平面标定板用于激光雷达和摄像机的标定,通过黑白棋盘格获取摄像头相对于车体的姿态外参数,通过平行板和倾斜板获取激光雷达的俯仰角和侧倾角;虽然其标定过程只需要一次就可以实现激光雷达和摄像机的联合标定,但是其标定板为立体标定板,加工精度高,标定过程复杂,在户外使用携带不方便。
结合叶春兰[11]提出的利用等腰直角三角板标定出激光雷达的俯仰角与安装高度以及彭梦等[10]使用黑白棋盘格标定出摄像机的内外参数,本文提出了利用梯形棋盘格标定板对单线激光雷达和摄像机进行标定的新方法。实验中只需要把梯形标定板放置在车辆的前方,采集一次数据就可以实现激光雷达坐标系与车体坐标系、摄像机坐标系和车体坐标系、激光雷达坐标系和摄像机坐标系之间的标定。
1 传感器标定原理摄像机以一定的角度和安装位置被固定在车辆上,摄像机完成的是将三维空间坐标系中的物体转换到二维图像坐标中。激光雷达和车体是刚性连接,两者间的相对姿态和位移固定不变。任意的激光雷达扫描点,在车体坐标系中存在唯一的点与之对应,在摄像机图像中也存在唯一的一个像素点与之对应,因此,对于在摄像机视角范围内的激光雷达扫描点,在图像像素坐标系中都存在一个像素点与之对应。
1.1 摄像机标定原理本文中选用的摄像机模型是针孔摄像机,针孔摄像机通过将三维空间中的点透视变换投影到图像平面上,将三维空间上的物体从环境坐标系转换至图像坐标系中, 摄像机模型的成像模型如图 1[12]所示。
|
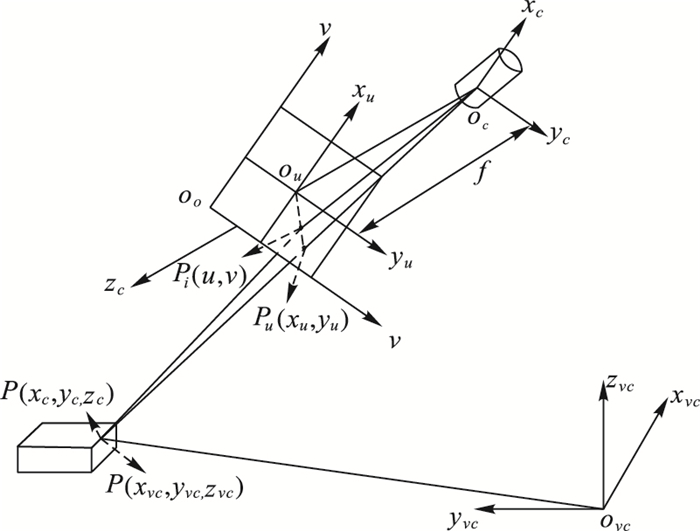
图 1 摄像机的透视变换模型 Figure 1 Perspective transformation model of camera |
图 1中,摄像机环境坐标系ovcxvcyvczvc指的是相机所在环境坐标系,即安装摄像机的车体坐标系。ocxcyczc是摄像机坐标系,ouxuyu为图像的物理坐标系,oouv为图像的像素坐标。投影指的是车体坐标系中的物点P(xvc, yvc, zvc)反射出的或者起源于光源的光线(光束)穿过光心oc射在像平面的点Pi(u, v)处,f是相机透镜的焦距。
车体坐标系中的物点P(xvc, yvc, zvc)到摄像机坐标系点P(xc, yc, zc)的转换关系为:
| $ \left[{\begin{array}{*{20}{c}} {{x_c}}\\ {{y_c}}\\ {{z_c}} \end{array}} \right] = {\boldsymbol{R}_{{\rm{veh}} \to {\rm{cam}}}}\left[{\begin{array}{*{20}{c}} {{x_{vc}}}\\ {{y_{vc}}}\\ {{z_{vc}}} \end{array}} \right] + {\boldsymbol{T}_{{\rm{veh}} \to {\rm{cam}}}} $ | (1) |
其中:Rveh → cam为3×3的坐标旋转矩阵;Tveh → cam为1×3坐标平移矩阵。Rveh → cam和Tveh → cam为摄像机的外部参数。
摄像机局部坐标系中的点P(xc,yc,zc)与图像像素坐标系中像点Pi(u, v)的转换关系:
| $ \left[{\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}\\ 0&{{f_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{x_c}/{z_c}}\\ {{y_c}/{z_c}}\\ 1 \end{array}} \right] $ | (2) |
其中:fx和fy分别为x方向和y方向的等效焦距;(u0, v0)为图像像素中心的坐标。fx、fy、u0、v0等参数为摄像机的内部参数,与摄像机和镜头的内部结构有关系。
1.2 等腰直角三角板标定激光雷达原理激光雷达在探测前方目标车辆过程中,主要用于确定车辆所在的候选区域,在实际应用中为了更好地定位车辆的位置应尽量减小安装的侧倾角。在安装激光雷达过程中,利用激光雷达扫描对称的物体,通过激光雷达成像调整激光雷达安装的侧倾角,使激光雷达的侧倾角近乎为0。激光雷达工作过程中,扫描模型如图 2所示。
|
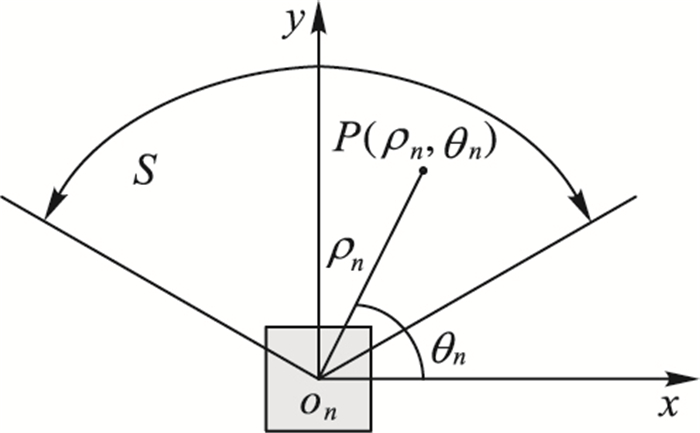
图 2 激光雷达扫描模型 Figure 2 LiDAR scanning model |
图 2中,角度S表示激光雷达扫描范围,(ρn, θn)表示在极坐标下激光雷达扫描点的距离和角度,其中,ρn是距离值,θn是对应角度。
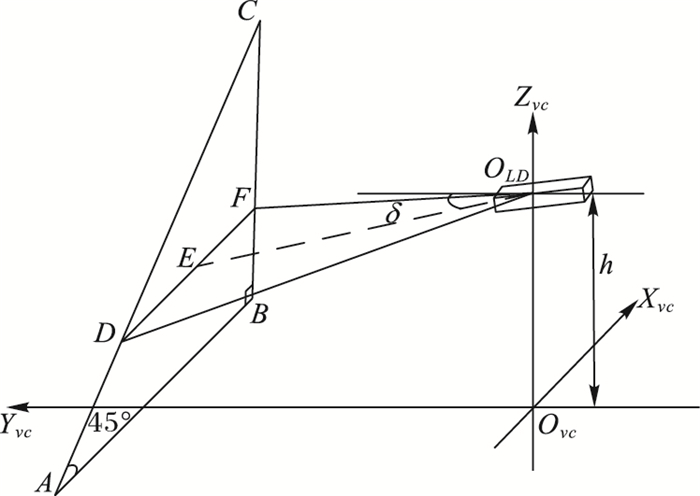
利用等腰直角三角板对激光雷达俯仰角和安装高度的标定效果如图 3所示。图 3中OLD为单线激光雷达的光心,Ovc为跟随车的质心,(xvc, yvc, zvc)为车体坐标系,DF为激光雷达扫描梯形板生成的扫描线, h为激光雷达安装高度。由于△ABC为等腰直角三角形,则CF=DF, BF=BC-CF=BC-DF, 根据余弦定理有:
|
图 3 利用等腰直角三角形对激光雷达进行标定 Figure 3 LiDAR calibration based on isosceles right triangle |
| $ DF = \sqrt {{\rho _{{O_{LD}}F}}^2 + {\rho _{{O_{LD}}D}}^2-2{\rho _{{O_{LD}}F}}{\rho _{{O_{LD}}D}}\cos ({\theta _{{O_{LD}}F}}-{\theta _{{O_{LD}}D}})} $ | (3) |
| $ \delta = \arcsin \left( {\frac{{h-BG}}{{{\rho _{{O_{LD}}F}} \cdot \sin ({\theta _{{O_{LD}}F}})}}} \right) $ | (4) |
由式(3) 和式(4) 联合建立约束方程,需要把标定板放置在不同的位置,求得多组方程,进而求解得到激光雷达的俯仰角δ和安装高度h。
将激光雷达坐标系下的参数转化到车体坐标系下的变换关系:
| $ \left[{\begin{array}{*{20}{c}} {{x_{vc}}}\\ {{y_{vc}}}\\ {{z_{vc}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \delta }&{\sin \delta }\\ 0&{-\sin \delta }&{\cos \delta } \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\rho _n}\cos ({\theta _n})}\\ {{\rho _n}sin({\theta _n})}\\ 0 \end{array}} \right] + \left[{\begin{array}{*{20}{c}} 0\\ 0\\ h \end{array}} \right] $ | (5) |
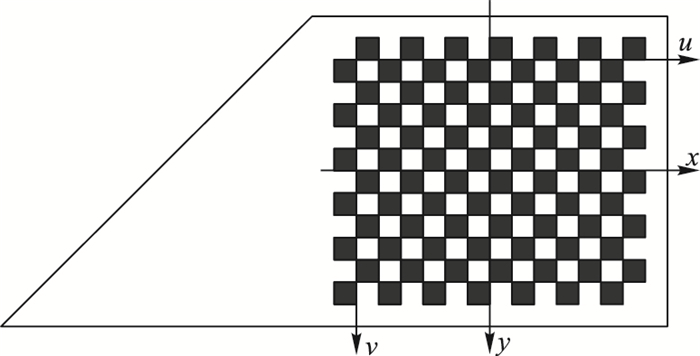
实验过程中,激光雷达扫描线是不可见的,根据等腰直角三角板能够标定出激光雷达的俯仰角与安装高度,黑白棋盘格能够标定出摄像机的内参数和车体坐标与摄像机坐标之间的外参数,设计了如图 4所示的标定板。图中所示为梯形标定板,右侧区域为黑白棋盘格,左侧区域为等腰直角三角形,把两者融合为一个直角梯形棋盘格。图 4中(x, y)坐标系表示标定板在摄像机图像成像中的物理坐标系,(u, v)坐标系表示标定板在摄像机图像成像中的像素坐标系。
|
图 4 梯形标定板的设计 Figure 4 Design of trapezoidal calibration plate |
由图 3可知利用等腰直角三角形标定板可以标定出激光雷达的俯仰角和安装高度,但是其需要放置在不同位置得到多个方程才能得到激光雷达的俯仰角和安装高度。本文实验把梯形标定板垂直放置在水平地面上,且水平地面区域视角广阔。由于激光雷达安装过程有向下的俯仰角,其前方照射的远点为前方的地面,根据这一信息可知,求取出所有激光雷达扫描点的距离乘以该点角度的正弦,求取最大值l=max(ρn·sin θn)。根据正弦定理,可以得知:
| $ \delta = \arcsin (h/(\max ({\rho _n} \cdot \sin ({\theta _n})))) $ | (6) |
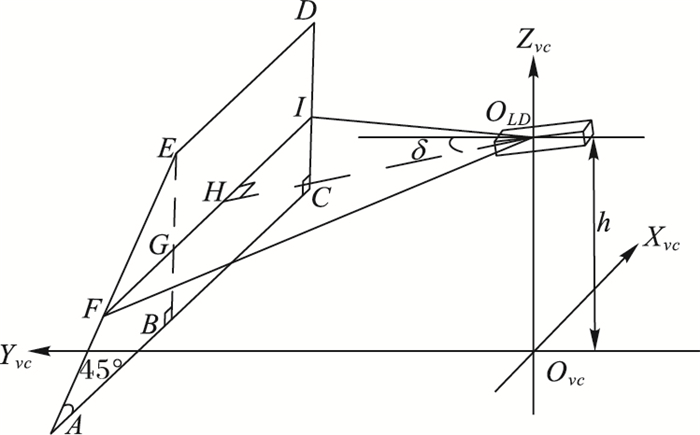
图 5为激光雷达扫描梯形棋盘格标定板的效果,FI为激光雷达扫描梯形板生成的扫描线。四边形BCDE为直角梯形,△ABE为等腰直角三角形,则FG=EG, BG=BE-EG=BE-FG, FG=FI-BC。得到扫描线在根据图中关系:
|
图 5 激光雷达俯仰角标定原理 Figure 5 Calibration principle of LiDAR pitch |
| $ FI = \sqrt {{\rho _{{O_{LD}}F}}^2 + {\rho _{{O_{LD}}I}}^2-2{\rho _{{O_{LD}}F}}{\rho _{{O_{LD}}I}}\cos ({\theta _{{O_{LD}}F}}-{\theta _{{O_{LD}}I}})} $ | (7) |
| $ \delta = \arcsin \left( {\frac{{h-BG}}{{{\rho _{{O_{LD}}I}} \cdot \sin ({\theta _{{O_{LD}}I}})}}} \right) $ | (8) |
联立式(6) 和式(8) 建立约束方程,进而求解得到激光雷达的俯仰角δ和安装高度h。
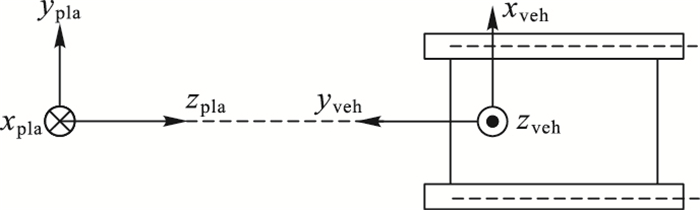
2.2 摄像机外参数的标定摄像机外参数的标定,实质是建立摄像机坐标系与车体坐标系的关系。在摄像机外参数标定过程中,将标定板平放在地面上容易造成图片变小,使得棋盘格角点定位误差变大。本文实验将棋盘格垂直放置在车辆的前方,棋盘格标定板在图像中的成像相对较大,角点提取的误差也较小,放置关系如图 6所示。其中,(xpla, ypla, zpla)为标定板的坐标。
|
图 6 车体坐标与棋盘格坐标示意图 Figure 6 Schematic diagram of car body coordinates and checkerboard coordinates |
由图 6知棋盘格坐标(xpla, ypla, zpla)与车体坐标(xvc, yvc, zvc)的旋转矩阵为:
| $ {\boldsymbol{R}_{{\rm{pla}} \to {\rm{veh}}}}{\rm{ = }}{R_y}({\rm{\pi /2}}){R_x}({\rm{\pi /2}}) = \left[{\begin{array}{*{20}{c}} 0&1&0\\ 0&0&{-1}\\ {-1}&0&0 \end{array}} \right] $ | (9) |
其中:Ry(π/2) 为棋盘格坐标(xpla, ypla, zpla)绕y轴方向旋转90°的旋转坐标,Rx(π/2) 为棋盘格坐标(xpla, ypla, zpla)绕x轴方向旋转90°的旋转坐标。
在标定过程中,摄像机坐标与标定棋盘格坐标两者之间的关系:
| $ \left[{\begin{array}{*{20}{c}} {{x_c}}\\ {{y_c}}\\ {{z_c}} \end{array}} \right] = {\boldsymbol{R}_{{\rm{pla}} \to {\rm{cam}}}}\left[{\begin{array}{*{20}{c}} {{x_{{\rm{pla}}}}}\\ {{y_{{\rm{pla}}}}}\\ {{z_{{\rm{pla}}}}} \end{array}} \right] + {\boldsymbol{T}_{{\rm{pla}} \to {\rm{cam}}}} $ | (10) |
其中:Rpla → cam为3×3棋盘格坐标到相机坐标的旋转矩阵,Tpla → cam为3×3棋盘格坐标到相机坐标的平移矩阵。
棋盘格坐标系与车体的坐标的关系为:
| $ \left[{\begin{array}{*{20}{c}} {{x_{vc}}}\\ {{y_{vc}}}\\ {{z_{vc}}} \end{array}} \right] = {\boldsymbol{R}_{{\rm{pla}} \to {\rm{veh}}}}\left[{\begin{array}{*{20}{c}} {{x_{{\rm{pla}}}}}\\ {{y_{{\rm{pla}}}}}\\ {{z_{{\rm{pla}}}}} \end{array}} \right] + {\boldsymbol{T}_{{\rm{pla}} \to {\rm{veh}}}} $ | (11) |
其中:Rpla → veh为3×3棋盘格坐标到车体坐标的旋转矩阵,Tpla → veh为3×3棋盘格坐标到车体坐标的平移矩阵。
联立式(9)~(11) 得:
| $ {\boldsymbol{R}_{{\rm{pla}} \to {\rm{cam}}}}{\rm{ = }}{\boldsymbol{R}_{{\rm{pla}} \to {\rm{cam}}}}\boldsymbol{R}_{{\rm{pla}} \to {\rm{veh}}}^{\rm{T}} $ | (12) |
为了获取棋盘格坐标与摄像机坐标之间的旋转矩阵Rpla → cam,通过建立棋盘格的角点在棋盘格坐标系下坐标M(x, y, z, 1) 和角点在图像中的像素齐次坐标m(u, v, 1) 之间的对应关系:
| $ \left[{\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \boldsymbol{H}\left[{\begin{array}{*{20}{c}} x\\ y\\ z\\ 1 \end{array}} \right] $ | (13) |
其中:H为3×4矩阵。然后由m和M对应点集合构成的线性方程求解,获得H的最小二乘解。其中:
| $ \boldsymbol{H} = \lambda \left[{\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}\\ 0&{{f_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right][{\boldsymbol{R}_{{\rm{pla}} \to {\rm{cam}}}}, {\boldsymbol{T}_{{\rm{pla}} \to {\rm{cam}}}}] $ | (14) |
其中λ为常数。在摄像机内参数已知的情况下,可以变换求解出棋盘格坐标与摄像机坐标之间的旋转矩阵Rpla → cam。
2.3 激光雷达和摄像机的联合标定根据2.1节激光雷达和2.2节摄像机标定过程分析可得激光雷达安装的俯仰角δ和安装高度h,摄像机的内参数和外参数。结合激光雷达和摄像机独立标定的结果可以对激光雷达和摄像机两个传感器进行联合标定,进而得到了激光雷达数据到摄像机图像像素之间的对应变换关系为:
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{f_x}}&0&{{u_0}}\\ 0&{{f_y}}&{{v_0}}\\ 0&0&1 \end{array}} \right].\\ \left( {{\boldsymbol{R}_{{\rm{veh}} \to {\rm{cam}}}}\left[{\begin{array}{*{20}{c}} {\frac{{{\rho _n}\cos ({\theta _n})}}{{-{\rho _n}\sin ({\theta _n})\sin (\delta ) + h}}}\\ {\frac{{{\rho _n}\sin ({\theta _n})\cos (\delta )}}{{-{\rho _n}\sin ({\theta _n})\sin (\delta ) + h}}}\\ 1 \end{array}} \right] + {\boldsymbol{T}_{{\rm{veh}} \to {\rm{cam}}}}} \right) \end{array} $ | (15) |
本实验选用的激光雷达的测量范围为0.1~50 m,角度分辨率为0.25°,扫描频率为25 Hz。摄像机分辨率为1294×964, 水平和垂直像素大小为3.75 μm,镜头的焦距为6 mm。实验是在一辆改装的半自主车辆上完成,激光雷达和摄像机固定在半自主无人车上,实验设备组成和安装关系如图 7所示。

|
图 7 实验设备组成和传感器安装关系 Figure 7 Experimental equipment and sensor installation |
图 7中激光雷达固定于车体的正前方中点,摄像机利用二轴云台固定于车体上方。激光雷达和摄像机的安装位置关系为:激光雷达在摄像机的前方约0.15 m, 摄像机处于激光雷达的上方,两者相距1 m,左右方向两者大致重合。梯形标定板由方形棋盘格板和等腰直角三角板拼接而成,梯形标定板的高度为0.7 m, 上边长为0.8 m, 下边长长度为1.5 m。标定时,梯形棋盘格放置于车辆的前方,让激光雷达和摄像机同步采集数据,摄像机的内参数通过Matlab标定工具箱已知,所以只需要采集一次激光雷达数据和摄像机图像即可以标定出激光雷达和摄像机坐标之间的变换矩阵。
为了评估本文方法的标定精度,对激光雷达扫描在梯形标定板的扫描点进行拟合,得到其在标定板上的位置。(udi, vdi)为提取点的实际图像坐标,(ui, vi)为根据式(15) 计算的投影点图像坐标。引入空间点的再投影位置偏差,如式(16) 描述:
| $ {R_e} = \frac{1}{N}\sum\limits_{i = 1}^N {\sqrt {{{({u_{di}}-{u_i})}^2} + {{({v_{di}}-{v_i})}^2}} } $ | (16) |
其中N是参与评估的测试点数。
根据上述评判标准,多次变换标定板的位置,得到多组数据,求得摄像机坐标与激光雷达坐标关系的标定精度为:平均精度Re=3.5691 pixel,实验所用的摄像机像元尺寸为3.75 μm/pixel, 折算后的精度为13.38 μm。
为了进一步验证本文方法,将本文方法与彭梦等[10]提出的基于双平行标定板方法进行对比分析。利用彭梦等[10]方法对本车上安装的激光雷达和摄像机进行了标定,并计算其再投影误差,结果如表 1所示。表 1从棋盘格坐标到相机坐标的旋转矩阵Rpla → cam、棋盘格坐标到相机坐标的平移矩阵Tpla → cam和平均位置偏差Re三个方面进行了比较。从表 1中可以看出:本文方法标定的棋盘格坐标到相机坐标的旋转矩阵Rpla → cam、棋盘格坐标到相机坐标的平移矩阵Tpla → cam与彭梦等[10]标定的非常接近,且在平均位置偏差Re方面优于彭梦等[10]的方法。
| 表 1 摄像机和激光雷达外参数联合标定结果 Table 1 Joint calibration results of external parameters of cameras and LiDAR |
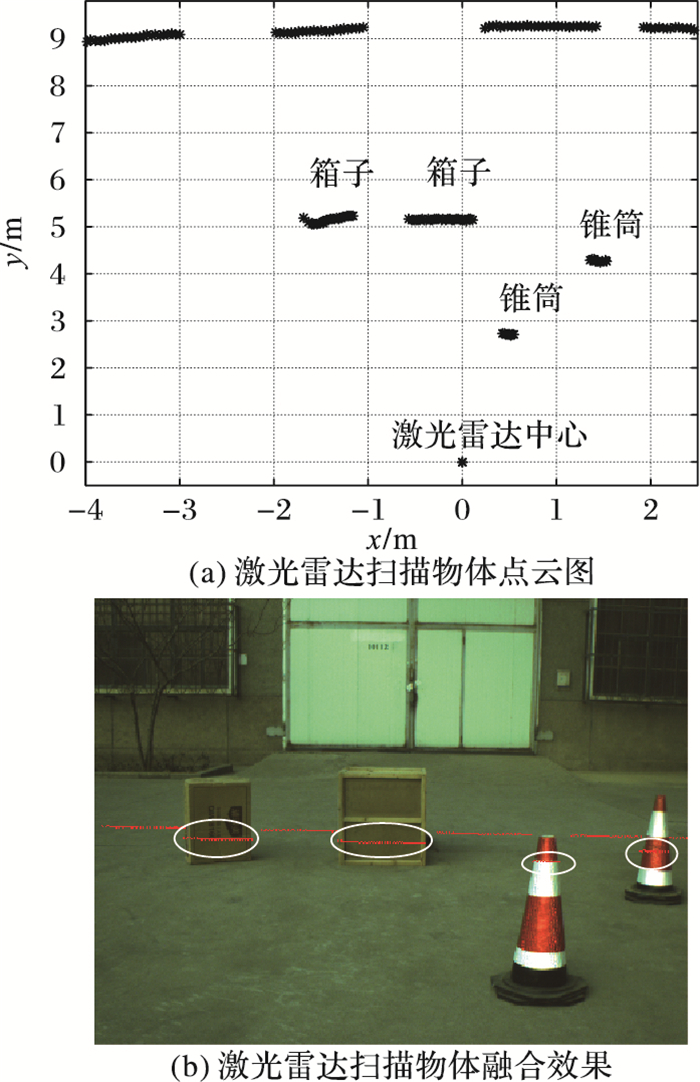
为了直观检验标定效果,将实验中的激光雷达扫描点投影到摄像机图像中。图 8(a)显示的是激光雷达扫描周围物体的点云图,展示了周围物体相对于激光雷达原点的距离和角度信息;图 8(b)显示的是激光雷达数据和摄像机图像之间的标定结果,白色圈内的点集代表激光雷达扫描点映射到图像上的位置。由于图 8中融合效果局部点不清晰,遂将激光雷达数据和摄像机图像像素级融合结果进行局部放大,效果如图 9所示。
|
图 8 激光雷达数据和图像融合结果 Figure 8 Fusion results of LiDAR data and image |

|
图 9 激光雷达数据和视觉图像融合效果放大图 Figure 9 Partial enlargement for fusion results of LiDAR data and image |
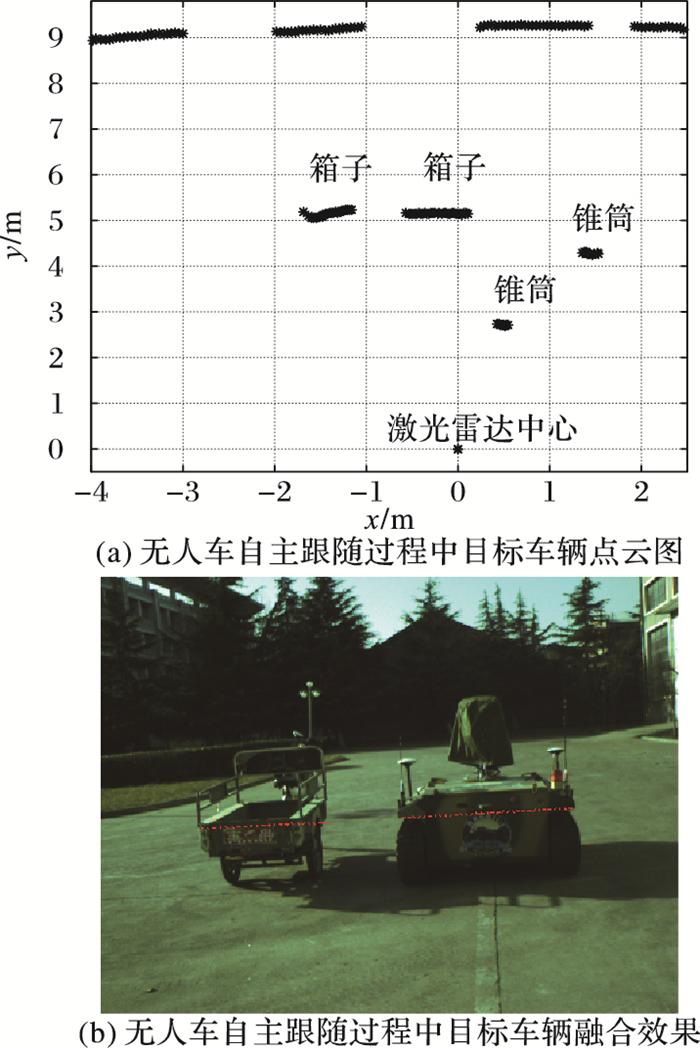
从图 9中可以看出箱子、锥桶等物体的各个边缘点得到较好的匹配,标定的结果基本满足实际情况。图 10显示的是在无人车自主跟随过程中,对目标车辆检测时激光雷达扫描点和摄像机图像融合的结果。从实验结果可以看出,不论是静止的静态物还是运动的车辆,配准的激光雷达扫描点与实际目标物图像都能够很好地匹配,可以满足无人车自主跟随过程的实际应用。
|
图 10 无人车跟随系统中激光雷达数据和图像融合效果 Figure 10 LiDAR data and image fusion in UGV leader-follower system |
本文针对车辆检测过程中激光雷达和摄像机的数据融合问题,采用梯形棋盘格标定板对单线激光雷达和摄像机进行联合标定,有效地建立激光雷达坐标系与车体坐标系、摄像机坐标系和车体坐标系、激光雷达坐标系和摄像机坐标系之间的对应关系,实现了激光雷达扫描点投影到图像上的像素级数据融合。实验过程中把梯形棋盘格标定板垂直放置在车辆前方,利用激光雷达和摄像机观察同一点时的空间约束,只要采集一次图像和激光雷达数据就可以满足整个标定过程,实现激光雷达扫描点投影到图像上的简单数据融合。实验结果表明,该方法标定的平均位置偏差为3.5691 pixel,折算后的精度为13 μm,标定精度高。同时从后续的融合效果来看,该方法融合效果好,具有较好的鲁棒性,为下一步的基于信息融合的车辆检测和车辆跟踪研究打下了良好的基础。后续将进行算法及标定方法优化,进一步提高标定精度和数据处理速度。
| [1] | ZHAO G Q, XIAO X H, YUAN J S, et al. Fusion of 3D-LiDAR and camera data for scene parsing[J]. Journal of Visual Communication and Image Representation, 2014, 25(1): 165-183. DOI:10.1016/j.jvcir.2013.06.008 |
| [2] | TAN J, LI J, AN X J, et al. Robust curb detection with fusion of 3D-Lidar and camera data[J]. Sensors, 2014, 14(5): 9046-9073. DOI:10.3390/s140509046 |
| [3] |
关超华. 智能车辆前方车辆检测与交通信号灯识别技术研究[D]. 北京: 北京理工大学, 2009: 37-68. GUAN C H. Study on technology of preceding vehicle detection and traffic light recognition for intelligent vehicle[D]. Beijing:Beijing Institute of Technology, 2009:37-68. |
| [4] | LIN K, CHANG C, DOPFER A, et al. Mapping and localization in 3D environments using a 2D laser scanner and a stereo camera[J]. Journal of Information Science and Engineering, 2012, 28(1): 131-144. |
| [5] | GAO C, SPLETZER J R. On-line calibration of multiple LiDARs on a mobile vehicle platform[C]//Proceedings of the 2010 International Conference on Robotics and Automation. Piscataway, NJ:IEEE, 2010:279-284. |
| [6] | 程金龙, 冯莹, 曹毓, 等. 车载激光雷达外参数的标定方法[J]. 光电工程, 2013, 40(12): 89-94. (CHENG J L, FENG Y, CAO Y, et al. Extrinsic calibration method for multiple LiDARs mounted on mobile vehicle[J]. Opto-Electronic Engineering, 2013, 40(12): 89-94. DOI:10.3969/j.issn.1003-501X.2013.12.015) |
| [7] | 刘大学, 戴斌, 李政, 等. 一种单线激光雷达和可见光摄像机的标定方法[J]. 华中科技大学学报(自然科学版), 2008, 36(S1): 68-71. (LIU D X, DAI B, LI Z, et al. A method for calibration of single line laser radar and camera[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2008, 36(S1): 68-71.) |
| [8] | ZHANG Q L, PLEASE R. Extrinsic calibration of a camera and laser range finder, WUCSE-2003-58[R]. St. Louis:Washington University in St. Louis, 2003. |
| [9] | PEREIRA M, SILVA D, SANTOS V, et al. Self calibration of multiple LiDARs and cameras on autonomous vehicles[J]. Robotics and Autonomous Systems, 2016, 83: 326-337. DOI:10.1016/j.robot.2016.05.010 |
| [10] | 彭梦, 蔡自兴. 一种基于双平行平面的激光雷达和摄像机标定方法[J]. 中南大学学报(自然科学版), 2012, 43(12): 4735-4742. (PENG M, CAI Z X. A practical method for calibration of laser radar and camera based on double parallel planes[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4735-4742.) |
| [11] |
叶春兰. 基于图像颜色与激光点云信息的智能车辆行驶环境三维重建[D]. 北京: 北京理工大学, 2013: 19-35. YE C L. The 3D reconstruction of intelligent vehicle driving environment base on the image color and laser point cloud information[D]. Beijing:Beijing Institute of Technology, 2013:19-35. |
| [12] |
STEGER C, ULRICH M, WIEDEMANN C. 机器视觉算法与应用[M]. 杨少荣, 吴迪靖, 段德山, 译. 北京: 清华大学出版社, 2010: 15-35. STEGER C, ULRICH M, WIEDEMANN C. Machine Vision Algorithms and Applications[M]. YANG S R, WU D J, DUAN D S, translated. Beijing:Tsinghua University Press, 2010:15-35. |




