组合实体造型(Constructive Solid Geometry, CSG)技术对多个简单几何实体通过交、并、差三种布尔运算组合可构建复杂几何形态(如图 1),所以广泛应用于某些拓扑结构复杂的产品外形设计中[1-3]。随着3D打印的兴起以及制造工艺的提高,使复杂拓扑结构的产品摆脱传统的手工雕刻加工转化为自动化加工成为可能,进而利用布尔运算设计复杂产品外形成为不可缺少的步骤。设计过程中需不断编辑单个图元然后反复进行布尔运算查看整体效果,对于复杂的网格模型编辑来说,布尔运算的稳定性以及效率成了设计瓶颈。以图 1(c)为例,涉及到的布尔运算总次数超过100次,而戒指外圈的每次修改将会导致这100次布尔运算的执行,而每个戒指的最终产品设计统计数据表明外圈的修改次数20次以上,从而会产生2000次布尔运算。在主流计算机辅助设计(Computer Aided Design, CAD)软件的测试结果(CATIA,Rhino,Solidworks)则通常需等候120 h以上(每次修改等待6 h),有些甚至直接告知无法进行运算,这对于设计所需立等可得的运算效率来说是难以接受的,极大限制了此类产品的设计效率,业界迫切需要对这一速度瓶颈进行突破。

|
图 1 需要利用大量布尔运算生成的复杂产品 Figure 1 Models with complex shapes via a large number of Boolean operations |
迄今为止,大部分研究[4-8]均是围绕如何构建有效包络盒(bounding box)来有效减小参与求交测试的三角面规模的思路进行:分别构建轴向包络盒(Axis Aligned Bounding Box,AABB)[4]、方向包络盒(Oriented Bounding Box, OBB)[5]、包围球[6]、K-Dop[7]、Hybrid[8]等, 此类方法对于超大规模的布尔运算来说仍然绕不开网格面片求交运算以及后期的碎片网格化的复杂运算,从而无法实现最终的快速布尔运算效果;还有学者基于重建的近似方法[9-10]来解决布尔运算存在的不稳定性问题, 主要包括体素法[11]、距离场(distance field)[12], level-set[13]、面元法(surfel)[14]、射线表示法[15-17]和八叉树[18]。
近期Wang等[19]利用网格离散化采样为点云,再利用点云通过内外判定获得最终布尔运算的结果点集;Adams等[20]利用八叉树分割点云和合理的边界单元分割方法实现了基于离散面片显示的布尔操作;Wang等[21]提出了基于点云的近似布尔运算与重构的方法,但未处理基于点云的布尔运算的相交线。除以上传统网格模型间的布尔运算研究外,最近有工作针对某些特殊网格模型的布尔运算进行了研究,包括:存在圆锥曲线或二次曲线边界的网格模型间的布尔运算[22]、多面体的网格模型间的布尔运算[23]以及B-rep表示网格模型间的布尔运算[24]。综上所述,现有工作均未涉及大规模网格模型间的布尔运算,在设计阶段如何瞬间响应获取设计结果的问题仍然没有解决,而本文着重解决此问题。
本文将三维网格模型间的布尔运算转化为一维射线段布尔运算,从而大大降低布尔运算的复杂度,规避了面面求交所导致的复杂计算和不稳定性,基于所获得的一维射线段模型布尔运算结果直接进行基于点云的渲染,较好地处理了相交边界,以及放大和缩小视图所导致的空洞缺陷,让最终结果在视觉上达到基于面片渲染的效果,从而满足设计过程中对于复杂拓扑结构产品设计中瞬间响应的实际工程要求。本文称这种一维布尔运算为视觉布尔运算,主要应用在产品的设计阶段,设计定型以后再通过之前的工作[25]进行快速的3D布尔运算(此时用户可以容忍等待较长时间),从而得到最终结果后进行后续的加工处理。
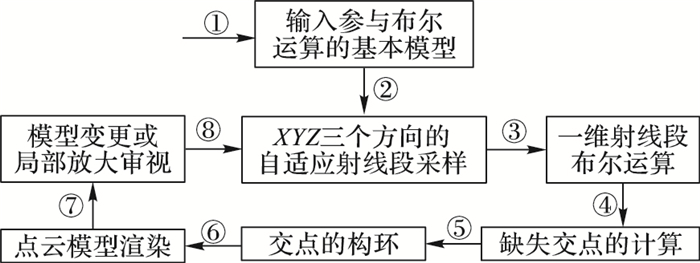
1 算法概述整个算法流程如图 2所示:首先输入参与布尔运算的各个几何基本体以及定义它们之间的布尔运算类型,形成CSG树形结构;步骤② 根据当前视窗的大小尺寸,利用显卡的GPU进行射线段的自适应射线段的采样(具有法线信息的3D像素模型),然后通过快速获取显存像素点的深度信息,进而获取每个像素的三维点位信息、贴图以及法线等关键信息;步骤③ 针对每条射线段进行一维的快速布尔运算;步骤④ 则判定出交点信息,并且插值计算出准确的交点的点位坐标以及相应的法线;步骤⑤ 则将所有的交点进行构环,从而填补由于采样精度误差所导致的直接渲染的孔洞暗点,获取较好视觉效果;步骤⑥ 直接对点云模型进行自适应的点渲染,获得比拟基于面片的渲染效果;如果在步骤⑦ 中,参与布尔运算的基本图形进行了修改或局部放大,则需局部位置进行再次自适应采样,从而在所发生变更的部位进行步骤② 至步骤⑥ 的流程。
|
图 2 3D布尔运算转化为1D视觉布尔运算的算法流程 Figure 2 Process of converting 3D mesh model Boolean operation to one among intervals in 1D |
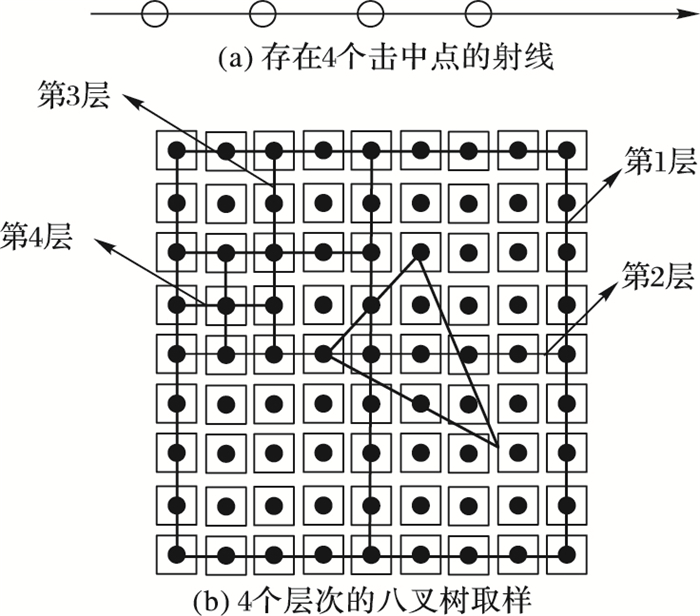
自适应射线段模型采样利用文献[25]的方法通过并行计算进行基于八叉树结构采样,快速实现网格模型到射线段模型的采样。该方法是假想沿着屏幕射出一系列射线束(如图 3(a)),射线束将会撞击到参与布尔运算的所有基本模型体上获得一系列的交点;而这些交点不是通过几何求交运算而是通过GPU从深度缓冲器和模板缓冲器快速获取。自适应采样则是采用八叉树的结构如图 3(b)示意,采样后的所有具有深度信息的像素点则在XYZ三个方向按坐标大小进行有序排列,交点XYZ方向的索引号记为(i, j, k)。
|
图 3 基于八叉树的射线段取样 Figure 3 Ray segment sampling in octree method |
根据像素在视窗中的XY方向的像素点坐标可利用转换矩阵调用gluUnProject函数直接获取三维点坐标,实际测试中发现该函数需要耗费大量计算资源,所以本文结合采样点在视窗中XY方向的像素视窗坐标,快速计算所有采样点的XYZ空间坐标:设想所有基本模型的整体包络盒记为BB, 该包络盒的左下顶点的空间坐标为(Xmin, Ymin, Zmin)右上顶点坐标为(Xmax, Ymax, Zmax);视窗的XY方向的物理分辨率分别为RX和RY,代表每两个像素间的实际物理距离,该值在模型绘制完成后可直接获知; 每个像素点的XY方向在视窗的像素坐标已知为
| $ \left\{ \begin{array}{l} {X_i} = {X_{\min }} + {{\dot X}_i}*{R_x}\\ {Y_i} = {Y_{\min }} + {{\dot Y}_i}*{R_y}\\ {Z_i} = {Z_{\min }} + {D_i}*({Z_{\max }}-{Z_{\min }}) \end{array} \right. $ |
由于采样点三维坐标的获取是通过在渲染管线渲染后取样,故存在一定的精度误差。为防止产生噪声点,获得模板缓冲值和深度缓冲值之前需设置好渲染环境,关掉抗锯齿功能、三角面片的偏置、灯光和抖动的功能。
| 表 1 犀牛软件算法与所提算法的耗时对比 Table 1 Time cost comparison of Rhino vs the proposed algorithm |
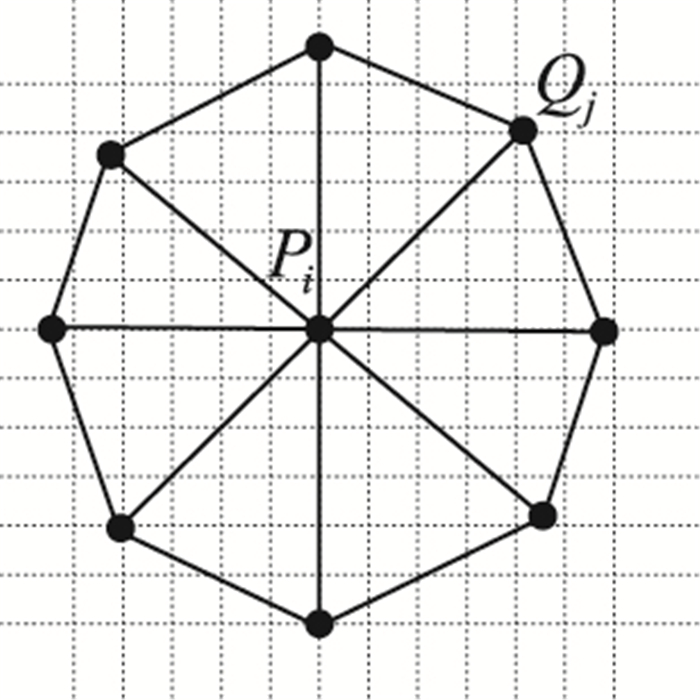
针对点云模型进行渲染前,获取每个像素的法线值对于渲染的光顺性非常重要。若该网格模型来自参数模型,则可直接计算该取样点的法线值;如果该模型是通过点云重建或者顶点法线信息缺失,则需拟合每个取样点的法线信息。文献[19]采用颜色索引值的方法获取每个采样点所属哪一个三角片,然后将三角片的面法线作为每个采样点的点法线;对该方法渲染时会出现面片棱角,仍需进行光顺处理。考虑到所有交点皆为有序排放,周围邻域点很容易获取,从而采用一种更为精确的近似方法进行取样点的法线赋值。如图 4所示,Pi点为待求法线的取样点。可以在XYZ方向,按照索引号i, j, k逐渐递增搜索的方法快速获取1-ring邻域的所有邻域点Qj,按照正投影进行快速排序构环三角化(参考本文构环算法),形成如图 4以Pi为中心的伞形结构,将构成扇形的所有三角片的单位面法线进行面积加权后的和作为最终Pi的法向量Ni。
|
图 4 点Pi法线的构建 Figure 4 Construction of normal vector at Pi |
取样建立射线段模型后,根据布尔运算的类型快速进行射线段间的布尔运算。本文解决的是大规模网格模型间布尔运算(单个模型三角片的数目超过50万)不能满足设计阶段所需的瞬间响应问题;在实际应用中参与运算的模型有可能需同时进行多次布尔运算,对于此种情况为提升速度,本文采用一次性采样,合并多次布尔运算为单次性布尔运算,从而可大大节省运算时间,满足设计所需的速度要求。布尔运算的实质是判定出哪些图元需要保留、哪些图元需要去掉,然后将保留下来的图元进行显示。对于本文特定应用,所有取样的射线段有序点保留/去除的规则遵循2.1节所描述的判定规则。
布尔运算的保留/去除判定如下所示。
所有射线段上的点的个数均应是偶数,奇数点的个数则对应为退化情况(射线段经过端点或者与面相切)。每个射线段上的取样点属于哪个基本体,则可以通过颜色映射快速获取:将所有参与布尔运算的基本体在显存中用不同颜色绘制,通过判断取样点所对应像素的颜色值确定该取样点属于哪个基本体。假设参与布尔运算的两个基本体分别为A和B(多个基本题的情况类似),针对差集A-B与B-A,并集A∪B以及交集A∩B确定射线段点的保留/去除原则。布尔运算则需指定射线段Lk的交点集合{Ps}保留/去除取样点的判定规则,从而获取需要保留的取样点。
由于实体模型的封闭特性,每条射线段Lk属于同一基本体的交点个数应为偶数:射入点与射出点成对并交替出现。对于奇数点数目的情况,则存在退化点,退化点通过邻域关系判可快速判断,并将该点处理成重合的两个点。在进行保留/去除判定之前需要完成内外判定,从而再根据布尔运算类型完成保留/去除判定规则。
内外判定如下所示。
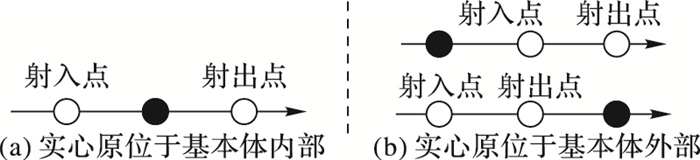
对于归属于同一基本体不失一般性记为A的一对射入点与射出点,如图 5绘制成空心圆圈;而属于物体B的所有取样点则是需要进行判断在物体A内或者外的点则标记为实心圆圈。对于同一条射线段,所有取样点按照深度信息的前后进行有序排列。如图 5,待判定的取样点(实心圆圈)如果位于基本体A中的射入点和射出点之间(如图 5(a)),则该点处于A的内部;否则是位于A的外部,即图 5(b)和5(c)两种情况。
|
图 5 射线段的内外判定 Figure 5 Inside/outside discrimination of ray segments |
保留/去除判定如下所示。
确定内/外判定法则以后则可以针对布尔运算类型从而快速确定取样点的保留/去除判定规则,该规则如下:
1)(A-B)差集保留/去除判定规则。
需要保留的点包括两种类型:① 所有位于B外部却属于A的点;② 所有位于A内部却属于B的点;其他的点则直接去除。
2)(B-A)差集保留/去除判定规则。
需要保留的点包括两种类型:① 所有位于A外部却属于B的点;② 所有位于B内部却属于A的点;其他的点则直接去除。
3)A∩B交集保留/去除判定规则。
需要保留的点包括两种类型:① 所有位于B内部却属于A的点;② 所有位于A内部却属于B的点;其他的点则直接去除。
4)A∪B并集保留/去除判定规则。
需要保留的点包括两种类型:① 所有位于B外部却属于A的点;② 所有位于A外部却属于B的点;其他的点则直接去除。
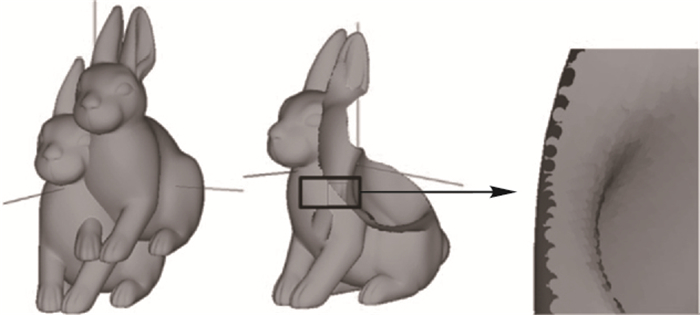
通过以上判定后,所有保留的取样点则构成最终布尔运算后的结果模型,该模型则由一系列的点构成,若这些点直接进行基于点(point disk)的渲染则会在交线处出现大量暗斑(如图 6),从而本文后续对交线处进行交点的插值后置处理。
|
图 6 交线区域产生的大量暗黑缺陷 Figure 6 Lots of darkness defects occurring along intersection curves |
经过布尔运算后的实体在两实体相交部分会产生较粗糙的边缘,在边缘处由于采样误差和相交点遮盖导致某些点的背面绘制出来形成暗点。该暗点可通过加大取样密度减小,但该方法存在两个问题:1) 取样密度的增加会显著增加运算量;2) 即便增加取样密度,仍无法消除暗点的产生,只是暗点区域变小,放大后该暗点仍然影响实际视觉效果。由于暗点的产生是取样精度所致,故本文在现有采样精度情况下插值交点,从而填补空缺,并构建交线环的方法来遮盖这些阴暗部位。
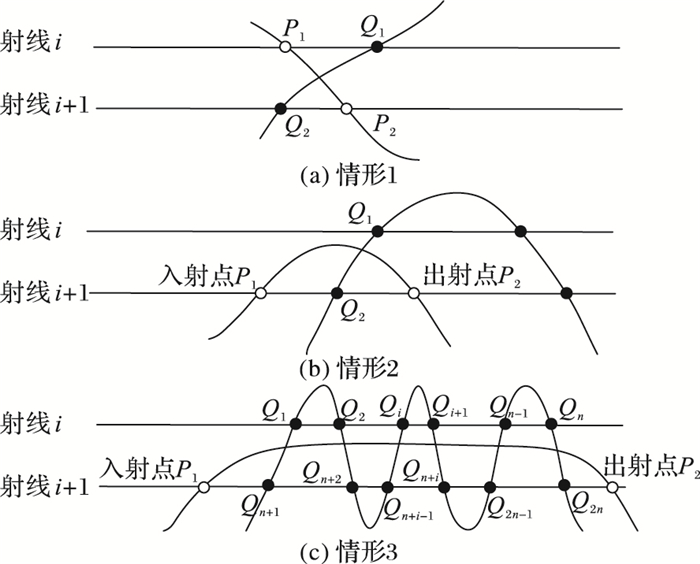
3.1 交点定位求解交点时需先知射线采样点的位置,通过前后两束射线采样点位置对比,判断相交点可能的位置,然后通过插值求取。设想射线沿着与坐标轴平行的方向逐层对所有基本体进行扫描,将会在过射线且与坐标平面平行的平面内得到一系列轮廓点,所有交点情况均可划分为以下3种情况之一或者组合:如图 7, Pi属于基本体A上的取样点,Qi则属于基本体B上的取样点。
|
图 7 相邻两射线段交点之间三种相对位置关系 Figure 7 Three relative locations of two adjacent ray segments |
相交情形1 如图 7(a), 紧邻的两条射线i与射线i+1上局部相邻位置分别存在P1,Q1和Q2和P2两个取样点。其中P1和P2属于基本体记为A,而Q1和Q2属于参与布尔运算的另一基本体。这种情形则是,基本体A在P1处的区域位于基本体B的内部(外部)而在P2处则变更为基本体B的外部(内部),所以在射线i与射线i+1之间存在交点。对于布尔运算的绝大部分相交情况属于此类。
相交情形2 如图 7(b), 此种情况是一种特殊相交情况,在射线i与射线i+1上局部区域内点的取样数目是不一样的,在此类情况中,取样基本体在取样区域从取样方向上看相对较为平缓,从而导致射线i+1上P1、P2两个交点跨度较大,无法构成情形1的交点相对位置关系,但此类情形亦容易判断:基本体A在Q1位置处于基本体B的外部(内部),而在Q2处则处于基本体B的内部,故基本体A与基本体B在射线i与i+1处存在交点。
相交情形3 如图 7(c),类似情形2,射线i与i+1上的取样点数目差别较大,通常表现为基本体A在射线i与i+1之间相对平缓,而基本体B则在此附近成多个波浪形,此时射线i只存在B的采样点,而射线i+1上存在基本体A上的一对射入点和射出点。
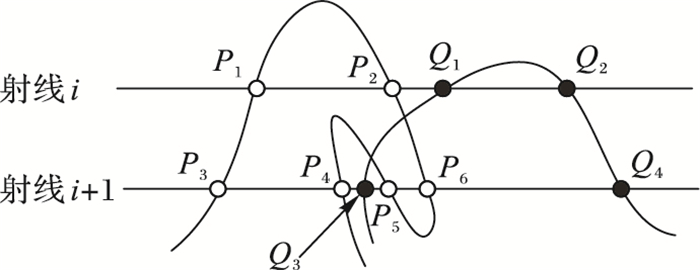
3.2 特殊情景处理确定三种相交情形后,针对相邻射线i与射线i+1,读取它们上的所有取样点,根据它们之间的相对位置关系很容易判断相交属于何种情况。本文所采取的存在交点的判断策略是:当基本体B在射线i上的取样点在基本体A的外部,而在射线段i+1时,B的部分或全部取样点位于基本体A内,此时射线i和射线i+1之间存在交点,其相交情景对应图 7的三种情况。如果参与运算的基本体轮廓非常复杂,存在大量的细小特征时,此原理在应用时存在以下例外:如图 8所示由于Q1和Q3均位于基本体A的外部,根据现有判定策略Q1和Q3之间是不存在交点的,这直接导致交点遗失;这种遗失产生的原因是,物体A在Q1和Q3之间存在尖锐的凸起或凹陷,对于此类情况处理如下:根据i+1线段一对进入进出点P5和P6相隔很近判断此处存在尖锐转折,而Q1位于P2的右端,相邻的Q3却位于P5的左端,这表明Q1和Q3间至少存在两个交点;此时应将P2,Q1和Q3和P6等同于情形1;而Q1,Q3和P4和P5等同于情形2。对于因细小凸起或凹陷均导致相邻一对射入点和射出点存在多个交点的情况,需首先通过相邻取样点距离判定存在细小凸起或凹陷,再根据以上方法将此情况分解为情形1和情形2的组合情况。值得一提的是,在很小局部空间内由于采样精度的限制,以上方法仍然可能遗失掉某些小于取样精度的交点,比如图 8中倘若基本体A在Q1和Q3中存在多个细小波浪,而根据现有方法本文只求取2个交点,从而会导致其他交点遗漏,但此种遗漏是可以接受的,因为小于取样精度的交点与所求取的2个交点位置非常近,对最后的视觉效果无影响。
|
图 8 尖锐凸起引起的特殊情况 Figure 8 Special case caused by sharp projections |
当相邻两射线段两采样点分别属于不同的物体且出现先后次序的交替时必产生交点。求解时,沿射线方向将所有取样点按深度递增的次序排序,剔除明显不会相交的线段和连续出现的属于同一物体的多条线段的点。然后按3.1节和3.2节确定相交的初步区域。由于获得采样点时的入射射线是离散的,入射射线正好射中相交点的概率极小,因此交点的高精度的近似获得需要通过相应计算。直观上讲,可以根据邻接关系构建二次曲线进行求交,考虑到通常情况的采样精度足够高,并且从效率上考虑本算法采用了线性插值的方法进行求解,实验也表明此种近似方法已经足够满足视觉精度要求。分别针对3.1节所描述的三种相交情形,对交点进行近似,其中近似交点标记为Mi:
对于情景1:线段P1P2和线段Q1Q2的交点作为基本体A和基本体B的交点;
对于情景2:Q1和Q2的中点作为交点;
对于情景3:Qi和Qn+i-1的中点作为系列交点。
通过以上步骤可以提取出相对较为精确的交点,并将交点添加到射线段采样点云模型中,则可以将阴影区域较好地遮盖。
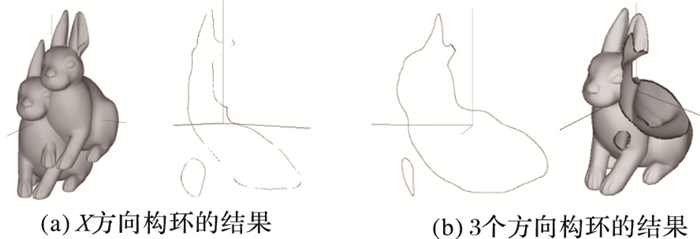
4 交点构环有时需要将交点构成环路进行高亮显示,从而使得整体轮廓分明,所以针对所获的无序交点,需进行构环操作。现所获取交点有以下特征:1) 沿某个采样射线上得到的交线环上的点沿交线环成单列分布;2) 交线上的点是不均匀的,点由沿着采样射线方向到与采样射线垂直方向由密变疏。由于采样发生在XYZ三个方向,根据基本体的结构,不同方向的采样密度存在差异,从而导致三个方向的交线环上的点相对于其他方向会产生一定程度上的微小偏移,由于微小偏移的存在,点不再沿着交线环成单列环状分布,而是沿着交线环随机分布(如图 9),所以利用如下方法获取沿交线环成单列分布的点集。
|
图 9 交线段的构环 Figure 9 Loop construction of intersection line-segments |
首先,对各方向上获得的点集分别进行以下操作:
1) 将所有交点分别复制到三个结构体数组,分别记为xArray、yArray和zArray并进行索引编号;
2) 对xArray按x坐标值升序排序,对yArray按y坐标值升序排序,以及对zArray按z坐标值升序排序;
3) 在xArray中取出第一个值,沿x轴以第一个点为中心往x增大和减小的方向同时搜索一个单位,将搜索得到的最小值作为当前与第一个点距离的最小值,接着分别进入y、z方向,重复x方向的动作。
经过前面三步可以获得离任意一点最近的点。接着,以xArray作为交线环上的原始数据点集,通过在稀疏的地方取出yArray或zArray中相应点补充进来。具体实施方法如下:
1) 从xArray中取出一点,检查该点处的法向量,得到最大法向量所在的方向,进入该方向的数组(yArray或zArray)并找出和该点最近的点,记为P0。
检查该数组中P0点并寻找下一点P1,检查P1的法向量是否为最大,并检查P0和P1之间的距离是否在给定的误差限定范围内,若P1满足条件则将P1取出放入目标数组Array,将P1点沿某一给定的向量移动一个微小位移,该向量的起点为前一次搜索的数组中的法向量开始小于其他方向的第一点,终点为目标数组中与第一个搜索点最近的点,若P1不满足条件则进入法向量值最大的数组搜索与该点最近的点P2。
2) 重复执行1) 直至找到某点与起始点的距离在给定的精度内则认为一个环已经被找到。
3) 回到该环起始点所在的数组,找出与该环起始点最近的点记为Pi,沿该点继续往前搜索,得到下一点Pj,若Pi和Pj的距离较大则将Pj作为下一个环的起始点,重复执行2) 和3),若Pi和Pj的距离在精度误差范围内则认为没有新的环了,停止搜索。
为消除因点云模型放大后产生的交线环上相邻两点间的距离过大现象,采取在两点间动态插入一定数目的点,使任意两点间的距离小于实际分辨率。
5 实现与分析基于三角面片的模型的布尔运算的时间主要消耗在可能相交的三角面片集的获取与交线环的提取上,随着三角面片数目的增多消耗的时间增加。本实例将在犀牛软件作为平台进行基于面片的布尔运算(如图 10~13),作为对比算法。实验中硬件开发环境CPU为AMD双核速龙Ⅱ X2, 主频为3.0 GHz,内存为3.5 GB,显卡为ATI radeon HD4250。软件开发环境为Windows 7操作系统,Visual Studio 2012开发平台,显示处理库为OpenGL。对比的参考量则是运行时间,分别就不同的取样分辨率进行了时间统计。其中实例1~3为两个几何体进行布尔运算,实例4和实例5则是多个基本体进行布尔运算。

|
图 10 兔子模型与兔子模型间的布尔运算(A-B) Figure 10 Mesh Boolean operation of A-B on two bunny models |
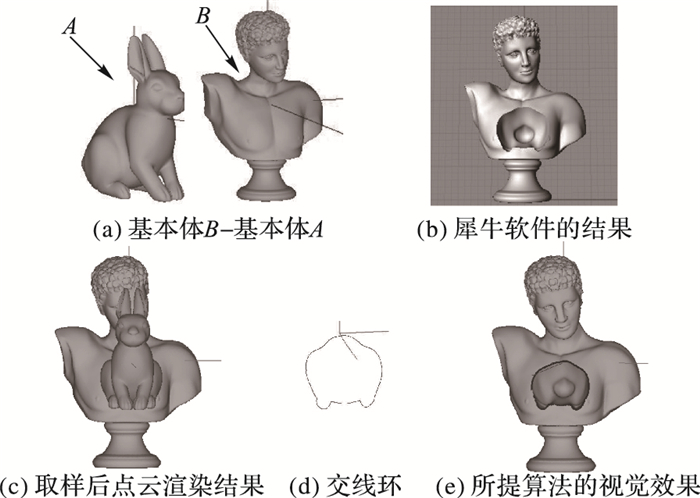
参考表 1,可明显发现所提算法具有明显速度优势,尤其对于网格密度大且图形拓扑结构相对复杂的情况(如图 11所示案例)优势更为明显。由于所提算法采用点云取样针对点云模型进行布尔运算,所以布尔运算的速度只与取样分辨率相关而与基本体的网格模型规模无关。对于基本体网格模型规模不大的情况(基本体网格数目小于104), 布尔运算次数不多时相差不大,但对于简单模型重复进行布尔运算时,所累积的优势会变得明显(如图 13)。通过表 1,可以看到这个速度完全可以用在产品设计阶段,在设计过程中用户可以立等可得布尔运算后的视觉效果,从而支持用户频繁修改单个图元从而进行多次查看最终设计效果。如果采用3D布尔运算则需要等待较长时间,从而大大影响设计效率。在实际应用中,采样密度通常采用视窗自适应的方式进行,首先获取所有图元的包络盒,然后在这个包络盒中采取视窗的显示分辨率(通常取128×128已足够观察细节);如需要查看更细节部位的结果则可通过视窗放大到需要查看的细节部位,让该部位充满视窗,然后利用本文方法再进行一次视觉布尔运算即可,由于此时查看时涉及到的布尔运算部件通常只有2~3个则此运算可以实时完成。产品设计阶段结束以后,则只需要进行最后一次的3D布尔运算,此时用户完全容忍等待较长时间,此时再利用之前的工作[25]快速完成3D布尔运算的3D结果模型的输出。
|
图 11 大卫模型与兔子模型的布尔运算(A-B) Figure 11 Boolean operation of A-B on David and bunny model |
|
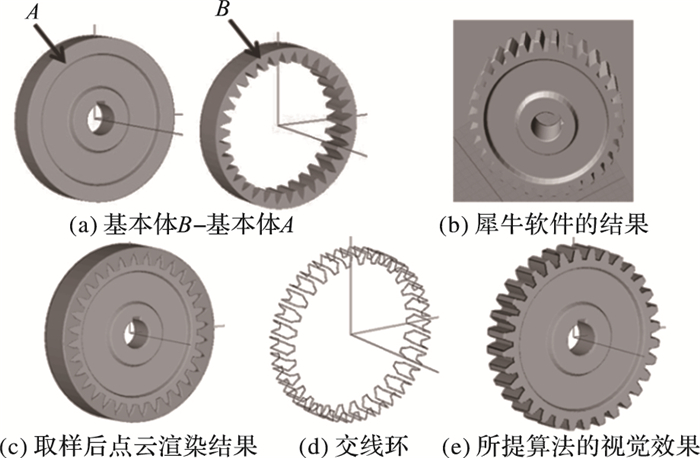
图 12 齿轮生成模型(A-B) Figure 12 Gear model by A-B |
|
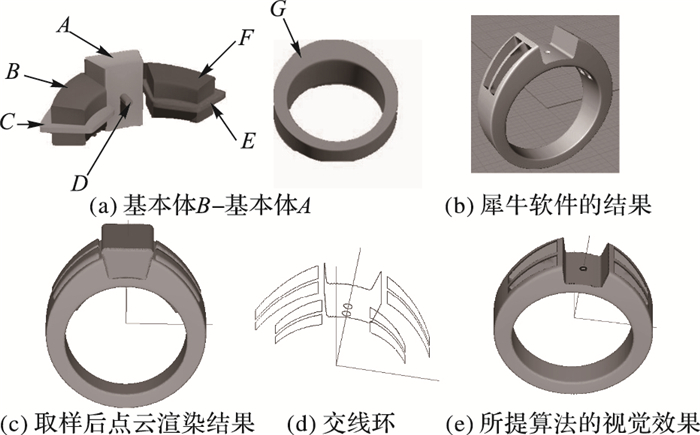
图 13 戒指生成模型G-[(B-C)+(A+D)+(F-E)] Figure 13 Ring model by G-[(B-C)+(A+D)+(F-E)] |
本文针对布尔运算在设计过程中运行时间慢的瓶颈进行了突破,能够支持工业产品设计时立等可得的渲染显示效果,从而使得产品设计的布尔运算效率极大提高。该算法采用基于GPU自适应的取样方法,将3D网格模型的布尔运算转变为一维的简单射线段模型的布尔运算,从而能极大提升算法效率和鲁棒性。该算法的运行效率与布尔运算基本体的网格模型规模及基本体的拓扑复杂性无关,而只与采样分辨率相关。总体运行时间对于128×128的分辨率情况可以达到实时效果,对于高分辨率情况亦可快速完成,对比网格模型的3D布尔运算具有上百倍的速度提升,而且显示效果同基于网格模型的渲染效果无异。该算法目前尚有提升空间,在后续工作中将就渲染效果以及分布式网格计算技术进行融合,从而能让大规模多次布尔运算达到瞬间响应的效果。
| [1] | 姜旭东, 盛斌, 马利庄, 等. 基于自适应延迟切割的三角网格布尔运算优化[J]. 软件学报, 2016, 27(10): 2473-2487. (JIANG X D, SHENG B, MA L Z, et al. Optimization of set operations on triangulated polyhedrons using adaptive lazy splitting[J]. Journal of Software, 2016, 27(10): 2473-2487.) |
| [2] | 蔡闯, 成思源, 杨雪荣. 基于特征分解的逆向建模技术研究[J]. 现代制造工程, 2016(2): 119-122. (CAI C, CHENG S Y, YANG X R. Research of reverse modeling technology based on feature decomposition[J]. Modern Manufacturing Engineering, 2016(2): 119-122.) |
| [3] | 王翀, 安伟强, 王红娟. 基于圆柱体-轴向包围盒检测的巷道相交建模[J]. 计算机应用, 2015, 35(12): 3592-3596. (WANG C, AN W Q, WANG H J. Tunnel intersection modeling based on cylinder-axis aligned bounding box[J]. Journal of Computer Applications, 2015, 35(12): 3592-3596. DOI:10.11772/j.issn.1001-9081.2015.12.3592) |
| [4] | VAN DEN BERGEN G. Efficient collision detection of complex deformable models using AABB trees[J]. Journal of Graphics Tools, 1997, 2(4): 1-13. DOI:10.1080/10867651.1997.10487480 |
| [5] | GOTTSCHALK S, LIN M C, MANOCHA D. OBB tree:a hierarchical structure for rapid interference detection[C]//Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques. New York:ACM, 1996:171-180. |
| [6] | HUBBARD P M. Collision detection for interactive graphics applications[J]. IEEE Transactions on Visualization and Computer Graphics, 1998, 1(3): 218-230. |
| [7] | KLOSOWSKI J T, HELD M, MITCHELL J S B, et al. Efficient collision detection using bounding volume hierarchies of k-DOPs[J]. IEEE Transactions on Visualization and Computer Graphics, 1998, 4(2): 21-36. |
| [8] | PAVIC D, CAMPEN M, KOBBELT L. Hybrid Booleans[J]. Computer Graph Forum, 2010, 29: 75-87. DOI:10.1111/cgf.2010.29.issue-1 |
| [9] | LORENSEN W E, CLINE H E. Marching cubes:a high resolution 3D surface construction algorithm[J]. ACM SIGGRAPH Computer Graphics, 1987, 21(4): 163-169. DOI:10.1145/37402 |
| [10] | KIM Y, VARADHAN G, LIN M C, et al. Fast swept volume approximation of complex polyhedral models[C]//Proceedings of the Eighth ACM Symposium on Solid Modeling and Application. New York:ACM, 2004:1013-1027. |
| [11] | CHEN Y, WANG C C L. Robust and accurate Boolean operations on polygonal models[C]//ASME 2007:Proceedings of the 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York:ACM, 2007:357-369. |
| [12] | JONES M W, BARENTZEN J A, SRAMEK M. 3D distance fields:a survey of techniques and applications[J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(4): 581-599. DOI:10.1109/TVCG.2006.56 |
| [13] | MUSETH K, BREEN D E, WHITAKER R T, et al. Level set surface editing operators[J]. ACM Transactions on Graphics, 2002, 21(3): 330-338. |
| [14] | ADAMS B, DUTRE P. Interactive Boolean operations on surfel-bounded solids[J]. ACM Transactions on Graphics, 2003, 22(3): 651-656. DOI:10.1145/882262 |
| [15] | MENON J P, VOELCKER H B. On the completeness and conversion of ray representations of arbitrary solids[C]//Proceedings of the 1995 International Proceedings of ACM Symposium on Solid Modeling and Applications. New York:ACM, 1995:175-286. |
| [16] | WANG C L. Approximate Boolean operations on large polyhedral solids with partial mesh reconstruction[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(6): 836-849. DOI:10.1109/TVCG.2010.106 |
| [17] | HEIDELBERGER B, TESCHNER M, GROSS M. Detection of collisions and self-collisions using image space techniques[J]. Journal of WSCG, 2004, 12(1/2/3): 145-152. |
| [18] | FEITO F R, OGAYAR C J, SEGURA R J, et al. Fast and accurate evaluation of regularized Boolean operations on triangulated solids[J]. Computer-Aided Design, 2013, 45(3): 705-716. DOI:10.1016/j.cad.2012.11.004 |
| [19] | WANG C C L, LEUNG Y S, CHEN Y. Solid modeling of polyhedral objects by layered depth-normal images on the GPU[J]. Computer-Aided Design, 2010, 42(6): 535-544. DOI:10.1016/j.cad.2010.02.001 |
| [20] | ADAMS B, DUTRE P. Interactive Boolean operations on surfel-bounded solids[J]. ACM Transactions on Graphics, 2003, 22(3): 651-656. DOI:10.1145/882262 |
| [21] | WANG C L. Approximate Boolean operations on large polyhedral solids with partial mesh reconstruction[J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(6): 836-849. DOI:10.1109/TVCG.2010.106 |
| [22] | WANG Z J, LIN X, FANG M E, et al. RE2L:an efficient output-sensitive algorithm for computing Boolean operations on circular-arc polygons and its applications[J]. Computer-Aided Design, 2017, 83: 1-14. DOI:10.1016/j.cad.2016.07.004 |
| [23] | LANDIER S. Boolean operations on arbitrary polygonal and polyhedral meshes[J]. Computer-Aided Design, 2016, 85: 138-153. |
| [24] | JIANG X, PENG Q, CHENG X, et al. Efficient Booleans algorithms for triangulated meshes of geometric modeling[J]. Computer-Aided Design and Applications, 2016, 13(4): 1-12. |
| [25] | CHEN M, CHEN X Y, TANG K, et al. Efficient Boolean operation on manifold mesh surfaces[J]. Computer-Aided Design and Applications, 2010, 7(3): 405-415. DOI:10.3722/cadaps.2010.405-415 |




