SIMON[1]是一类特别适合于资源受限环境的超轻量级分组密码。自2013年被美国国家安全局提出以来,SIMON受到了学者广泛关注, 主要攻击方法包括:线性攻击[2]、不可能差分攻击[3-4]、代数攻击[5]、立方攻击[6]。与其他轻量级分组密码不同,绝大部分SIMON密码要求的门电路数小于1 000(轻量级分组密码要求门电路数小于2 000),这使得SIMON在硬件和软件方面均表现出良好的性能。
故障攻击[7]是一种利用密码设备在外界干扰下(温度、电压、电磁脉冲等)[8-9]产生的故障行为或错误信息来恢复密钥的攻击方法。它由Boneh等在1996年首次提出,并成功破解了RSA(Rivest-Shamir-Adleman)签名算法。1997年,Biham等[10]将差分思想与故障攻击结合,提出了差分故障攻击(Differential Fault Attack, DFA)。2010年,Courtois等[11]提出代数故障攻击(Algebraic Fault Attack, AFA)思想,解决了差分故障攻击手工分析复杂、故障信息利用率低、通用性差的问题,实现了故障攻击的自动化。此后,研究者又对PRESENT[12]、Piccolo[13]等密码进行了代数故障攻击。
目前关于SIMON的故障攻击研究现状如下:在FDTC2014上,Tupsamudre等[14]假设故障注入倒数第2轮左半部分,利用单比特模型和单字节模型,通过差分推导得出结论“至少需要n/2个单比特故障或者n/8个单字节故障可以恢复最后一轮n比特轮密钥”。Takahashi等[15]针对同样的注入位置,将故障宽度扩展到半轮。他们主要分析了SIMON核心部件‘ & ’的差分特性。实验结果表明,仅需要7.82个故障可以恢复SIMON128/128的全部轮密钥。在FDTC2015上,Vásquez等[16]在文献[14]基础上,将单比特故障注入位置加深1轮,利用相似的差分分析方法,降低了攻击所需要的故障数量同时减少了选取的故障注入位置。
尽管对SIMON的差分故障攻击取得了较好的攻击效果,但是上述研究存在如下问题:1) 故障深度较小。由于故障注入较深轮时,故障传播路径复杂,差分攻击难以根据最后一轮输出推断出故障的传播情况,因此差分攻击往往只能实现浅轮故障注入的分析;2) 差分攻击需要复杂的手工推导,自动化、通用性较差。
针对上述问题,本文给出SIMON密码代数故障攻击。主要工作和创新点如下:1) 采用单比特故障已知和故障未知模型对SIMON32/64进行代数故障攻击,故障位置选取第26轮,两种模型分别仅需5个和6个故障即可恢复全部密钥,优于文献[16]所需的50.85个故障;2) 采用n比特宽度故障已知和未知模型对SIMON128/128进行代数故障攻击,故障位置选取第65轮,两种模型均只需2个故障即可恢复全部密钥,优于文献[15]所需的7.82个故障;3) 对比故障已知和未知模型,发现当故障数较小时,故障信息量与密钥求解时间成反比,而当故障数较大时,故障信息量与密钥求解时间成正比。
1 SIMON系列密码SIMON系列轻量级分组密码采用平衡Feistel结构。为了提高算法灵活性,设计者提供了10个版本,均可用SIMON 2n/mn表示(如表 1)。其中:n代表字长,2n表示分组长度,mn表示密钥长度。这10个版本分别为:32/64,48/72,48/96,64/96,64/128,96/96,96/144,128/128,128/192,128/256。本文选择的研究对象是SIMON32/64、SIMON128/128。
| 表 1 SIMON系列密码参数 Table 1 Parameters of SIMON ciphers |
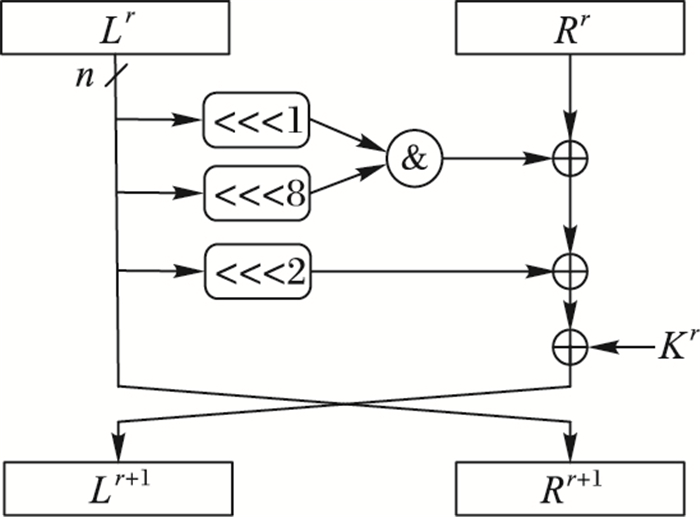
SIMON轮函数(见图 1)包含3种操作:按位异或(⊕)、按位与( & )、循环左移( < < < )。
|
图 1 SIMON轮函数 Figure 1 Round function of SIMON |
设Lr和Rr分别表示经过r轮加密后中间状态的左半部分和右半部分,则对于轮密钥Kr∈GF(2)n, SIMON每一轮加密过程可以用式(1) 表示:
| $ {\left\{ \begin{array}{l} {L^{r + 1}} = F({L^r}) \oplus {R^r} \oplus {K^r}\\ {R^{r + 1}} = {L^r} \end{array} \right.} $ | (1) |
其中F(Lr)=((Lr < < < 1) & (Lr < < < 8))⊕(Lr < < < 2)。
1.2 密钥扩展算法SIMON系列分组密码的轮函数是相同的,其不同之处在于密钥扩展算法。假设初始密钥为K0,K1,…,Km-1, 利用轮密钥递推公式可以得到全部轮密钥K0,K1,…,Kr-1。根据初始密钥字长m不同,递推公式分为3种:
| $ {K^i} = \left\{ \begin{array}{l} {K^{i - 2}} \oplus ({K^{i - 1}} > > > 3) \oplus ({K^{i - 1}} > > > 4) \oplus c \oplus {({z_j})_{i - m}},m = 2\\ {K^{i - 3}} \oplus ({K^{i - 1}} > > > 3) \oplus ({K^{i - 1}} > > > 4) \oplus c \oplus {({z_j})_{i - m}},m = 3\\ {K^{i - 4}} \oplus (Q \oplus (Q > > > 1)) \oplus c \oplus {({z_j})_{i - m}},Q = {K^{i - 3}} \oplus ({K^{i - 1}} > > > 3),m = 4 \end{array} \right. $ |
其中,常量c=0xff…fc,c的二进制位数与轮密钥Ki相同。z0, z1, z2, z3, z4是5个不同的二进制常量数列,不同版本的SIMON密码可采用不同的z,关于z0, z1, z2, z3, z4数列的具体值可以参考文献[1]。
2 代数故障攻击框架如图 2所示,P、C、K分别代表明文,密文以及初始密钥。假设U表示故障注入轮的中间状态,Uf表示故障注入后的中间状态,KU表示从故障注入轮到最后一轮的轮密钥集合,则正确明文C=F(U, KU),而错误密文C*=F(Uf, KU)。正确加密和错误加密过程之间最明显的关联是:ΔU=U⊕Uf,ΔC=C⊕C*。此外,如果能够推断出故障注入位置,通过分析故障传播路径,还可以得到更多关于正确、错误加密的关系式。一般的代数故障攻击共分为3步。

|
图 2 AFA框架 Figure 2 AFA framework |
1) 构建正确加密过程代数方程。
在代数攻击中,为充分利用明文和密文信息,首先要构建全轮加密过程的代数方程。这需要攻击者对密码的轮函数以及密钥扩展算法进行深入的分析;更重要的是,他们能够将一种密码的核心操作表示成代数方程,例如S盒、模加运算、‘ & ’运算等。
2) 故障信息利用。
首先,攻击者需要决定故障模型,一个故障模型由3部分组成:故障注入位置,故障宽度以及故障是否已知。故障注入位置可以是某一轮,也可以是某一轮的一部分,例如在文献[14]中选取倒数第二轮左半部分。故障宽度是指一次故障注入可能会影响到的比特位数,典型的故障宽度有:1(bit),4(Nibble),8(Byte)。故障是否已知是指攻击者在注入故障后,是否知道故障准确信息。故障已知模型侧重于理论分析,主要用于探究密码特性,而故障未知模型更加侧重实际,用于评估密码的安全性。在确定了故障模型后,便可分析故障传播路径,列出关于故障信息的代数方程。一个有效方程要保证同时包含正确加密变量和错误加密变量。
3) 代数方程组求解。
在将正确加密过程和故障信息全部转化为代数方程后,需要利用一定的方法来求解。由于方程数量较大,一般有4种方法:基于可满足性问题(SATisfiability problem, SAT)的方法(借助Minisat、CryptoMinisat等解析器),基于优化的方法(借助CPLEX、SCIP解析器),基于线性化的方法(直接线性化、扩展线性化)以及基于Gröbner基的方法。本文采取第一种方法,利用CryptoMinisat-2.9.6进行求解。
3 对SIMON32/64的代数故障攻击 3.1 密钥扩展算法和轮函数的代数方程构建作为SIMON密码的核心部件,‘ & ’操作可以通过降次实现。由于在SAT方法中,所有运算都需要转化为异或(⊕)和合取(∨)操作,因此可以利用式(2) 所示方法,对‘ & ’进行转化。对于代数方程x1 & x2⊕x3⊕x4⊕x5⊕x6=0,引入q=x1 & x2,可将其转化为式(3):
| $ {x_1}\& {x_2} = q \Rightarrow \left\{ \begin{array}{l} {x_1} \vee \overline q = 1\\ {x_2} \vee \overline q = 1\\ \overline {{x_1}} \vee \overline {{x_2}} \vee q = 1 \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} q \oplus {x_3} \oplus {x_4} \oplus {x_5} \oplus {x_6} = 0\\ {x_1} \vee \overline q = 1\\ {x_2} \vee \overline q = 1\\ \overline {{x_1}} \vee \overline {{x_2}} \vee q = 1 \end{array} \right. $ | (3) |
对于SIMON32/64的密钥扩展算法,引入4组变量tmp1、tmp2、tmp3、tmp4,利用如下操作来表示整个过程,引入变量个数16×4×28=1 792, 方程个数16×5×28=2 240。
for i=4 to 31
tmp1=Ki-1>>>3;
tmp2=tmp1⊕Ki-3;
tmp3=tmp2>>>1;
tmp4=tmp2⊕tmp3;
Ki=Ki-4⊕tmp4⊕zji-m⊕c;
end
此外,引入tmp5、tmp6、tmp7、tmp8,利用如下操作表示SIMON32/64全轮正确加密过程,引入变量个数16×4×32=2 048, 方程个数(5×16+3×16)×32=4 096。
for i=1 to 32
Ri=Li-1;
tmp5=Li-1 < < < 1;
tmp6=Li-1 < < < 8;
tmp7=Li-1 < < < 2;
tmp8=tmp5 & tmp6;
Li=tmp8⊕tmp7⊕Ri-1⊕Ki-1;
end
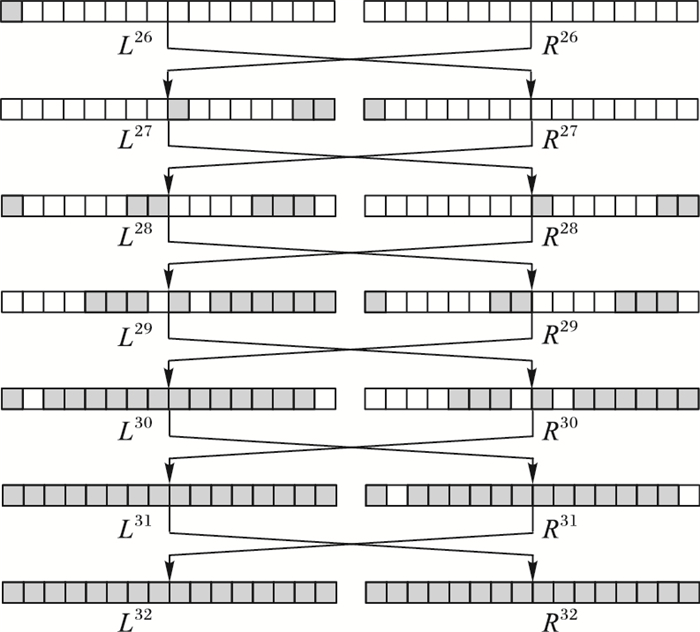
3.2 故障模型设定对SIMON32/64的攻击采用单比特模型。为充分利用故障信息,尽可能将故障位置注入较深轮。经过简单估算,发现将单比特故障注入倒数第7轮时,最后一轮刚好可以覆盖全部比特,此时故障信息利用程度最高,因此选择L26作为故障注入位置。单比特故障注入L26, 0时的故障传播路径如图 3所示。
|
图 3 单比特故障注入L26, 0时的故障传播路径 Figure 3 Fault propagation path of single-bit fault injected in L26, 0 |
首先,构建倒数6轮错误加密过程代数方程。除此之外,在故障已知情况下,还可以找出更多关于正确和错误加密中间状态比特的关系式。以图 3为例,假设故障注入L26, 0,可以得到式(4)~(10)。当故障注入L26,R26其余位置时,故障信息表示的代数方程组与此类似。
| $ \left\{ \begin{array}{l} L{'_{27,8}} = {L_{26,9}}\& L{'_{26,0}} \oplus {L_{26,10}} \oplus {R_{26,8}} \oplus {K_{26,8}}\\ L{'_{27,14}} = {L_{26,15}}\& {L_{26,6}} \oplus L{'_{26,0}} \oplus {R_{26,14}} \oplus {K_{26,14}}\\ L{'_{27,15}} = L{'_{26,0}}\& {L_{26,7}} \oplus {L_{26,1}} \oplus {R_{26,15}} \oplus {K_{26,15}} \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} L{'_{28,0}} = L{'_{27,8}}\& {L_{27,1}} \oplus {L_{27,2}} \oplus R{'_{27,0}} \oplus {K_{27,0}}\\ L{'_{28,6}} = L{'_{27,14}}\& {L_{27,7}} \oplus L{'_{27,8}} \oplus {R_{27,6}} \oplus {K_{27,6}}\\ L{'_{28,7}} = L{'_{27,15}}\& L{'_{27,8}} \oplus {L_{27,9}} \oplus {R_{27,7}} \oplus {K_{27,7}}\\ L{'_{28,12}} = {L_{27,4}}\& {L_{27,13}} \oplus L{'_{27,14}} \oplus {R_{27,12}} \oplus {K_{27,12}}\\ L{'_{28,13}} = {L_{27,5}}\& L{'_{27,14}} \oplus L{'_{27,15}} \oplus {R_{27,13}} \oplus {K_{27,13}}\\ L{'_{28,14}} = {L_{27,6}}\& L{'_{27,15}} \oplus {L_{27,0}} \oplus {R_{27,14}} \oplus {K_{27,14}} \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} L{'_{29,4}} = L{'_{28,12}}\& {L_{28,5}} \oplus L{'_{28,6}} \oplus {R_{28,4}} \oplus {K_{28,4}}\\ L{'_{29,5}} = L{'_{28,13}}\& L{'_{28,6}} \oplus L{'_{28,7}} \oplus {R_{28,5}} \oplus {K_{28,5}}\\ L{'_{29,6}} = L{'_{28,14}}\& L{'_{28,7}} \oplus {L_{28,8}} \oplus {R_{28,6}} \oplus {K_{28,6}}\\ L{'_{29,8}} = L{'_{28,0}}\& {L_{28,9}} \oplus {L_{28,10}} \oplus R{'_{28,8}} \oplus {K_{28,8}}\\ L{'_{29,10}} = {L_{28,2}}\& {L_{28,11}} \oplus L{'_{28,12}} \oplus {R_{28,10}} \oplus {K_{28,10}} \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} L{'_{29,11}} = {L_{28,3}}\& L{'_{28,12}} \oplus L{'_{28,13}} \oplus {R_{28,11}} \oplus {K_{28,11}}\\ L{'_{29,12}} = {L_{28,4}}\& L{'_{28,13}} \oplus L{'_{28,14}} \oplus {R_{28,12}} \oplus {K_{28,12}}\\ L{'_{29,13}} = {L_{28,5}}\& L{'_{28,14}} \oplus {L_{28,15}} \oplus {R_{28,13}} \oplus {K_{28,13}}\\ L{'_{29,14}} = L{'_{28,6}}\& {L_{28,15}} \oplus L{'_{28,0}} \oplus R{'_{28,14}} \oplus {K_{28,14}}\\ L{'_{29,15}} = L{'_{28,7}}\& L{'_{28,0}} \oplus {L_{28,1}} \oplus R{'_{28,15}} \oplus {K_{28,15}} \end{array} \right. $ | (7) |
| $ \left\{ \begin{array}{l} L{'_{30,0}} = L{'_{29,8}}\& {L_{29,1}} \oplus {L_{29,2}} \oplus R{'_{29,0}} \oplus {K_{29,0}}\\ L{'_{30,2}} = L{'_{29,10}}\& {L_{29,3}} \oplus L{'_{29,4}} \oplus {R_{29,2}} \oplus {K_{29,2}}\\ L{'_{30,3}} = L{'_{29,11}}\& L{'_{29,4}} \oplus L{'_{29,5}} \oplus {R_{29,3}} \oplus {K_{29,3}}\\ L{'_{30,4}} = L{'_{29,12}}\& L{'_{29,5}} \oplus L{'_{29,6}} \oplus {R_{29,4}} \oplus {K_{29,4}}\\ L{'_{30,5}} = L{'_{29,13}}\& L{'_{29,6}} \oplus {L_{29,7}} \oplus {R_{29,5}} \oplus {K_{29,5}}\\ L{'_{30,6}} = L{'_{29,14}}\& {L_{29,7}} \oplus L{'_{29,8}} \oplus R{'_{29,6}} \oplus {K_{29,6}}\\ L{'_{30,7}} = L{'_{29,15}}\& L{'_{29,8}} \oplus {L_{29,9}} \oplus R{'_{29,7}} \oplus {K_{29,7}}\\ L{'_{30,8}} = {L_{29,0}}\& {L_{29,9}} \oplus L{'_{29,10}} \oplus {R_{29,8}} \oplus {K_{29,8}}\\ L{'_{30,9}} = {L_{29,1}}\& L{'_{29,10}} \oplus L{'_{29,11}} \oplus {R_{29,9}} \oplus {K_{29,9}}\\ L{'_{30,10}} = {L_{29,2}}\& L{'_{29,11}} \oplus L{'_{29,12}} \oplus {R_{29,10}} \oplus {K_{29,10}}\\ L{'_{30,11}} = {L_{29,3}}\& L{'_{29,12}} \oplus L{'_{29,13}} \oplus {R_{29,11}} \oplus {K_{29,11}}\\ L{'_{30,14}} = L{'_{29,6}}\& L{'_{29,15}} \oplus {L_{29,0}} \oplus R{'_{29,14}} \oplus {K_{29,14}} \end{array} \right. $ | (8) |
| $ \left\{ \begin{array}{l} L{'_{31,0}} = L{'_{30,8}}\& {L_{30,1}} \oplus L{'_{30,2}} \oplus {R_{30,0}} \oplus {K_{30,0}}\\ L{'_{31,1}} = L{'_{30,9}}\& L{'_{30,2}} \oplus L{'_{30,3}} \oplus {R_{30,1}} \oplus {K_{30,1}}\\ L{'_{31,2}} = L{'_{30,10}}\& L{'_{30,3}} \oplus L{'_{30,4}} \oplus {R_{30,2}} \oplus {K_{30,2}}\\ L{'_{31,3}} = L{'_{30,11}}\& L{'_{30,4}} \oplus L{'_{30,5}} \oplus {R_{30,3}} \oplus {K_{30,3}}\\ L{'_{31,7}} = {L_{30,15}}\& L{'_{30,8}} \oplus L{'_{30,9}} \oplus {R_{30,7}} \oplus {K_{30,7}}\\ L{'_{31,9}} = {L_{30,1}}\& L{'_{30,10}} \oplus L{'_{30,11}} \oplus {R_{30,9}} \oplus {K_{30,9}}\\ L{'_{31,13}} = L{'_{30,5}}\& L{'_{30,14}} \oplus {L_{30,15}} \oplus R{'_{30,13}} \oplus {K_{30,13}}\\ L{'_{31,14}} = L{'_{30,6}}\& {L_{30,15}} \oplus L{'_{30,0}} \oplus R{'_{30,14}} \oplus {K_{30,14}}\\ L{'_{31,15}} = L{'_{30,7}}\& L{'_{30,0}} \oplus {L_{30,1}} \oplus R{'_{30,15}} \oplus {K_{30,15}} \end{array} \right. $ | (9) |
| $ \left\{ \begin{array}{l} L{'_{32,1}} = L{'_{31,9}}\& L{'_{31,2}} \oplus L{'_{31,3}} \oplus {R_{31,1}} \oplus {K_{31,1}}\\ L{'_{32,15}} = L{'_{31,7}}\& L{'_{31,0}} \oplus L{'_{31,1}} \oplus {R_{31,15}} \oplus {K_{31,15}} \end{array} \right. $ | (10) |
本文提出另外一种方法来表示故障信息而无需知道故障注入具体位置。对于SIMON32/64倒数第7轮,正确的中间状态和故障注入后的中间状态可分别表示为L26, 0|L26, 1|…|L26, 31和L′26, 0|L′26, 1|…|L′26, 31。二者的差分用ΔL26=ΔL26, 0|ΔL26, 1|…|ΔL26, 31表示,其中ΔL26, i=L26, i⊕L′26, i(0≤i < 32)。引入32个变量:x0, x1, …, x31,对xi(0≤i < 32) 有xi=1⊕ΔL26, i。如果单比特故障位于第i比特,则有xi=0,xj≠0(j≠i, 0≤j < 32)。也就是说集合X={x0, x2, …, x31}中只有一个元素是0,其余为1,这一关系可用式(11)、(12) 表示:
| $ (1 \oplus {x_0}) \vee (1 \oplus {x_1}) \vee ... \vee (1 \oplus {x_{31}}) = 1 $ | (11) |
| $ {x_u} \vee {x_v} = 1{\rm{ ; 0}} \le u < v \le 31 $ | (12) |
如图 4所示,T为SIMON128/128总轮数,文献[15]采用的故障位置是LT-2,故障宽度为半轮长度n bit。该文献通过分析‘ & ’的差分特性,能够恢复SIMON128/128全部密钥,且仅需要7.82个故障。本文试图将故障注入位置加深1轮,故障宽度不变,进一步证明代数故障攻击的有效性。
4.2 故障已知模型全轮正确加密代数方程组构建与3.1节类似,这里不再赘述,主要关注故障信息的利用。以故障值ΔLT-3=0x 01 00 00 00 08 00 00 00为例,得到其故障传播路径如图 5所示,故障信息的代数方程表示与3.3节中类似。但是,总共有264种ΔLT-3,不可能把它们全部表示出来。这里采取一种动态的方法:每次攻击根据故障值推断出故障传播情况并且动态地构建代数方程组。

|
图 5 故障值ΔLT-3=0x 01 00 00 00 08 00 00 00时的故障传播路径 Figure 5 Fault propagation path of fault value ΔLT-3=0x 01 00 00 00 08 00 00 00 |
一种动态的代数故障攻击步骤如下:
1) 根据ΔLT-3推断故障传播路径。
假设Xt, m(T-3≤t≤T, 0≤m≤127) 表示t轮第m比特的故障传播情况,Xt, m=1表示该比特受到了故障传播的影响(不一定会发生翻转),而Xt, m=0则表示不会受到影响。通过分析SIMON轮函数,容易得到Xt, m的迭代计算公式,如式(13) 所示:
| $ {X_{t,m}} = \left\{ \begin{array}{l} \Delta {L_{T - 3,m}}{\rm{, }}t = T - 3{\rm{ }}and{\rm{ }}0 \le m < 64\\ 0,{\rm{ }}t = T - 3{\rm{ }}and{\rm{ }}64 \le m < 128\\ {X_{t - 1,m - 64}}{\rm{, }}T - 3{\rm{ < }}t{\rm{ }}and{\rm{ }}64 \le m < 128{\rm{ }}\\ {X_{t - 1,(m + 1)\% 64}}|{X_{t - 1,(m + 2)\% 64}}|{X_{t - 1,(m + 8)\% 64}}|{X_{t - 1,m + 64}},T - 3{\rm{ < }}t{\rm{ }}and{\rm{ }}0 \le m < 64{\rm{ }} \end{array} \right. $ | (13) |
2) 动态地构建故障信息代数方程。
对所有Xt, m=1(0≤m≤63),通过判断Xt-1, (m+1)%64、Xt-1, (m+2)%64、Xt-1, (m+8)%64、Xt-1, m+64的值,可以动态地构建关于Xt, m的代数方程(14):
| $ \begin{array}{l} {L_{t,m}} = ({L_{t - 1,(m + 1)\% 64}}\;{\rm{ or }}\;L{'_{t - 1,(m + 1)\% 64}})\& ({L_{t - 1,(m + 8)\% 64}}\;{\rm{ or }}\;L{'_{t - 1,(m + 8)\% 64}})\\ \oplus ({L_{t - 1,(m + 2)\% 64}}\;{\rm{ or }}\;L{'_{t - 1,(m + 2)\% 64}}) \oplus ({R_{t - 1,m}}\;{\rm{ or }}\;R{'_{t - 1,m}}) \oplus {K_{t - 1,m}} \end{array} $ | (14) |
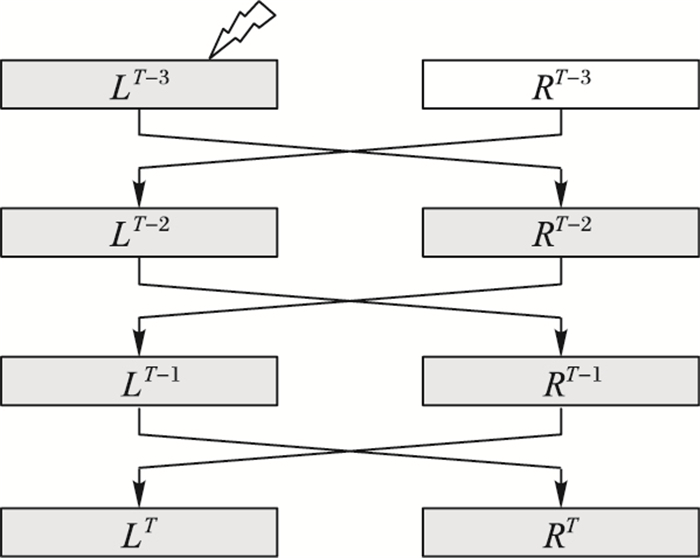
本文提供另外一种模型,在该模型下攻击者不需要知道故障值。如图 6所示,为了更好地同故障已知模型比较,故障注入位置仍选取LT-3。尽管故障传播的内部结构无法知道,但利用错误密文仍然可以构建代数方程。对每次故障注入,将后3轮的错误加密过程用代数方程表示出来,并代入错误密文。此时,中间状态LT-3可看成是全新的变量,而RT-3保持与全轮正确加密时同样的值,该值不变是正确加密与错误加密过程的唯一联系。即使如此,由于故障宽度较大,涉及的密钥信息较多,在故障未知的情况下利用代数故障攻击仍可求出唯一解,后续仿真实验验证了这一结论。
|
图 6 SIMON128/128故障未知模型 Figure 6 Fault-unknown model of SIMON128/128 |
本文利用C++语言(Visual C++6.0) 模拟故障注入过程,并通过程序将代数方程组全部写入一个记事本,最后使用CryptoMinisat解析器进行密钥求解。解析器版本为2.9.6,程序运行环境如下:Intel i5-4570芯片, 3.20 GHz, 4.00 GB内存, Windows 7(32位)操作系统。
5.2 SIMON32/64攻击结果下面给出一个攻击实例。
1) SIMON32/64全轮正确加密方程构建。
固定初始密钥K(K0, K1, K2, K3)=0x 0100 0908 1110 1918,随机生成明文P=0x 9ae5 173a,正确加密产生密文C=0x 99e3 7944。利用3.1节所述方法构建全轮正确加密代数方程组。
2) 故障注入及故障信息利用。
利用程序仿真故障注入过程,在第26轮注入单比特随机故障,4次实验得到4个错误密文:C1=0x 4d03 5804, C2=0x 01f5 de92, C3=0x d817 2131, C4=0x 670b 9b97。在故障已知模型下,假设攻击者已知故障注入位置,可以利用该信息,而在故障未知模型下,则不能使用该信息。根据3.3、3.4节所述方法构建故障信息方程,在故障已知模型下,总共引入8 083个变量,10 469个代数表达式,脚本大小约189 KB。在故障未知模型下,总共引入8 173个变量,11 921个代数表达式,脚本大小约为204 KB。
3) 基于SAT的代数方程组求解。
利用CryptoMinisat执行代数方程组脚本,在两种模型下得到相同结果,如表 2所示,初始密钥64比特编号为2~65,其中编号为负代表密钥值是0,编号为正代表密钥值是1。根据表 2,求得的密钥值是:0000000100000000000010010000100000010001000100000001100100011000, 转换为十六进制,即:0x 0100 0908 1110 1918, 求解结果正确。
| 表 2 解析器求解代数方程组结果 Table 2 Results of CryptoMinisat-2.9.6 |
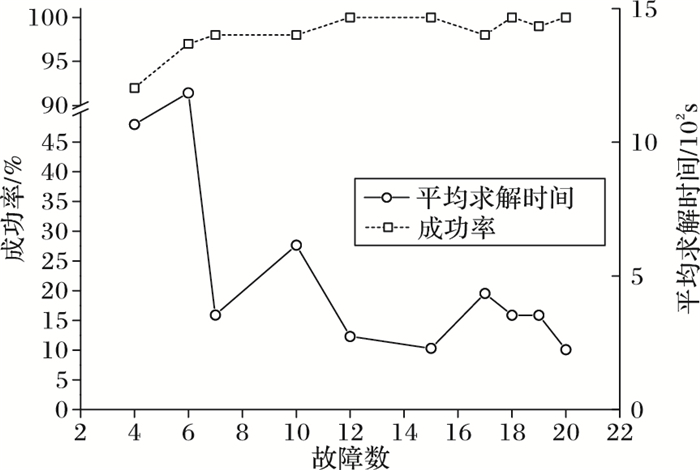
此外,提高故障数作进一步实验。当密钥求解时间超过3 600 s时,认为攻击失败。对每个故障数,分别执行100次攻击,观察攻击成功率和平均求解时间随故障数增长的变化情况(见图 7~8)。得出下列结论:

|
图 7 故障已知模型不同故障数攻击结果 Figure 7 Attack results of fault-known model with different fault numbers |
|
图 8 故障未知模型不同故障数攻击结果 Figure 8 Attack results of fault-unknown model with different fault numbers |
1) 在故障已知模型中,当故障数≥5时,攻击成功率≥99%,因此为保证成功率故障数至少为5。此外,观察发现当故障数≥7时,利用CryptoMinisat-2.9.6解析器求解时间均小于1 s。
2) 在故障未知模型中,当故障数≥6时,攻击成功率≥97%,因此为保证成功率故障数至少为6。当故障数为20时,平均求解时间仍然有224 s,可见求解速度大大低于故障已知模型,这是由于该模型可利用的故障信息较少。
3) 一般情况下,随故障数增加成功率会提高,而平均求解时间会降低,但图 8中的折线出现一定的波动,原因是:随着故障数增加,虽然信息量多了,但过多的方程数可能增加了计算负担,使得求解时间出现反弹。
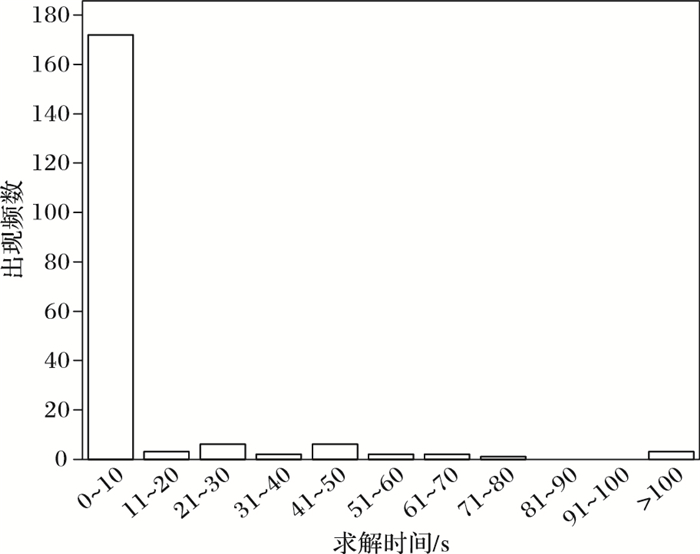
5.3 SIMON128/128攻击结果对SIMON128/128的仿真实验与SIMON32/64类似。实验表明,利用两种模型对SIMON128/128进行代数故障攻击,均只需要2个故障即可实现。在两种模型下,利用2个故障分别执行200次攻击实验,求解时间分布如图 9~10所示。结果表明:在故障已知模型中,大部分随机数据可以在10 s内得出结果,而在故障未知模型中需要的时间则相对较多。这主要是由于两种模型能够利用的故障信息量不同导致的。上述两种模型攻击成功率分别为98.5%和94.81%。
|
图 9 故障已知模型求解时间分布(故障数=2) Figure 9 Solving time distribution of fault-known model with 2 faults |

|
图 10 故障未知模型求解时间分布(故障数=2) Figure 10 Solving time distribution of fault-unknown model with 2 faults |
此外,进一步增加故障数量,对于每个故障数分别作200组随机数据攻击实验。如图 11所示,当故障数>2时,两种模型平均求解时间均小于1 s。观察发现:故障已知模型一开始平均求解时间低于故障未知模型,这是由于故障已知模型中可以获得的故障信息更多;但随着故障数的递增,故障已知模型的平均求解时间开始高于故障未知模型,因为此时两种模型的故障信息都已足够,代数方程数量成为了决定求解时间的主要因素。

|
图 11 两种模型平均求解时间随故障数变化 Figure 11 Average solving time of two models with fault number growing |
本文对SIMON密码代数故障攻击结果与已有工作的比较如表 3~4所示。代数故障攻击与差分故障相比,具有下列优点:1) 故障注入深度较大。代数故障攻击无需进行具体推导,只要列出描述故障信息的代数方程即可,因此它能够实现较深轮的故障分析。2) 故障数较少。由于代数故障攻击能够将故障注入较深轮,且能充分利用故障信息,因此它所需的故障数大大低于差分故障攻击。3) 攻击通用性强,自动化程度高。差分故障攻击需结合具体密码进行推导,相比之下,代数故障攻击方法相对固定,且攻击过程利用解析器完成,自动化程度较高。
| 表 3 对SIMON32/64的攻击结果 Table 3 Summary of fault attack on SIMON32/64 |
| 表 4 对SIMON128/128的攻击结果 Table 4 Summary of fault attack on SIMON128/128 |
本文对SIMON32/64和SIMON128/128进行代数故障攻击,相比原有差分故障攻击,提高了故障深度,大大减少了所需故障数,且整个攻击过程通用性强、自动化程度高。SIMON密码的设计者主要考虑了算法实现的简易,而没有考虑代数故障攻击的可能性,因此需要对密码设备加强防护以防范此类攻击。
| [1] | BEAULIEU R, SHORS D, SMITH J, et al. The SIMON and speck families of lightweight block ciphers[EB/OL]. (2013-06-19)[2017-01-16]. http://eprint.iacr.org/2013/404.pdf. |
| [2] | ALIZADEH J, BAGHERI N, GAURAVARAM P, et al. Linear cryptanalysis of round reduced SIMON[EB/OL]. (2014-10-16)[2017-01-16]. http://eprint.iacr.org/2013/663.pdf. |
| [3] | ALKHZAIMI H A, LAURIDSEN M M. Cryptanalysis of the SIMON family of block ciphers[EB/OL]. (2013-08-28)[2017-01-16]. http://eprint.iacr.org/2013/543.pdf. |
| [4] | ALIZADEH J, ALKHZAIMI H A, AREF M R, et al. Cryptanalysis of SIMON variants with connections[C]//RFIDSec 2014:Proceedings of the 10th Workshop on Radio Frequency Identification:Security and Privacy Issues. Berlin:Springer, 2014:90-107. |
| [5] | RADDUM H. Algebraic analysis of the SIMON block cipher family[C]//LatinCrypt 2015:Proceedings of the Fourth International Conference on Cryptology and Information Security in Latin America. Berlin:Springer, 2015:157-169. |
| [6] | 万刘蝉, 韦永壮. 简化SIMON类算法的立方测试与分析[J]. 计算机应用研究, 2017, 34(1): 246-250. (WAN L C, WEI Y Z. Cube test and analysis for reduced SIMON family of block ciphers[J]. Application Research of Computers, 2017, 34(1): 246-250.) |
| [7] | BONEH D, DEMILLO R A, LIPTON R J. On the importance of checking cryptographic protocols for faults[C]//EUROCRYPT 1997:Proceedings of the 14th Annual EUROCRYPT Conference on the Theory and Applications of Cryptologic Techniques. Berlin:Springer, 1997:37-51. |
| [8] | BAR-EL H, CHOUKRI H, NACCACHE D, et al. The sorcerer's apprentice guide to fault attack[EB/OL]. (2004-05-07)[2017-01-16]. http://eprint.iacr.org/2004/100.pdf. |
| [9] | FUKUNAGA T, TAKAHASHI J. Practical fault attack on a cryptographic LSI with ISO/IEC 18033-3 block ciphers[C]//FDTC 2009:Proceedings of the 2009 Fault Diagnosis and Tolerance in Cryptography. New York:ACM, 2009:84-92. |
| [10] | BIHAM E, SHAMIR A. Differential fault analysis of secret key cryptosystems[C]//CRYPTO 1997:Proceedings of the 17th Annual International Cryptology Conference. Berlin:Springer, 1997:513-525. |
| [11] | COURTOIS N, WARE D, JACKSON K. Fault-algebraic attacks on inner rounds of DES[EB/OL]. (2010-09-22)[2017-01-16]. http://www.nicolascourtois.com/papers/dfasolv.pdf. |
| [12] | 吴克辉, 赵新杰, 王韬, 等. PRESENT密码代数故障攻击[J]. 通信学报, 2012, 33(8): 85-92. (WU K H, ZHAO X J, WANG T, et al. Algebraic fault attack on PRESENT[J]. Journal on Communications, 2012, 33(8): 85-92.) |
| [13] | 赵新杰, 郭世泽, 王韬, 等. Piccolo密码代数故障分析研究[J]. 计算机学报, 2013, 36(4): 882-894. (ZHAO X J, GUO S Z, WANG T, et al. Research of algebraic fault analysis on Piccolo[J]. Chinese Journal of Computers, 2013, 36(4): 882-894.) |
| [14] | TUPSAMUDRE H, BISHT S, MUKHOPADHYAY D. Differential fault analysis on the families of SIMON and SPECK ciphers[EB/OL]. (2014-05-30)[2017-01-16]. http://eprint.iacr.org/2014/267.pdf. |
| [15] | TAKAHASHI J, FUKUNAGA T. Fault analysis on SIMON family of lightweight block ciphers[C]//ICISC 2014:Proceedings of the 2014 International Conference on Information Security and Cryptology. Berlin:Springer, 2014:175-189. |
| [16] | VáSQUEZ J C G, BORGES F, PORTUGAL R, et al. An efficient one-bit model for differential fault analysis on SIMON family[C]//FDTC 2015:Proceedings of the 2015 Fault Diagnosis and Tolerance in Cryptography. Washington DC:IEEE Computer Society, 2015:61-70. |





