随着互联网技术的飞速发展以及3D扫描、3D打印等计算机硬件技术的进步,三维模型的数据量与复杂度逐步提高,针对海量三维模型的形状分析、模型检索、模型压缩、资源重组等应用研究日益广泛,三维模型的形状对应与匹配得到了越来越多学者们的关注。
目前常用的三维模型匹配方法有基于骨架的匹配方法[1-4]、基于点的收敛性匹配方法[5-9]、基于几何距离优化的交互式3D模型匹配方法[10-12]、基于稀疏化模型的内蕴对应匹配分析[13-16]。文献[2]提出Reeb模式进行模型局部配准方法,通过Reeb表和碟状或环状的拓扑结构进行图形分割,然后结合参数优化建立简洁有效的子区域结构描述符实现模型的形状匹配。但这种方法易受模型表面变化的影响,只在处理同类模型数据和目标时有很强的稳定性。基于点收敛性匹配方法早期由文献[5]提出,其采用迭代最近点(Iterative Closest Point, ICP)算法使得两个图形中点的距离最小;在此基础上文献[6-9]又提出了优化匹配样板,但都无法避免对于较大数据特别是在噪声干扰情况下,耗时长、匹配过程易产生较大误差的缺陷。文献[11]提出了一种截然不同的方法,通过扰动分析方法展示移除的模型部分对拉普拉斯-贝尔特拉米特征函数的改变,并利用它作为对应的频谱,结合变量优化和函数加权的方法实现模型的对应。文献[12]通过稀疏化模型实现内蕴匹配是近年来的研究热点,无需使用任何的特征描述符即能实现重复区域的查找检测,即使是残缺模型也适用此方法, 但这种方法最大的缺点就是必须对模型进行统一有效的区域分割得到模型稀疏化表示。文献[17]通过Mumford-Shah算法规范建立基于局部对应的描述符而非基于点对的特征描述符,提高了运行效率, 但是这种方法必须要建立区域成对的局部描述符。
为了进一步提高三维模型匹配的效率和稳定性,揭示模型之间的内蕴结构对应性,本文提出了一种融合热核与局部体积特征的三维模型相似性分析方法。通过提取模型的内蕴特征,即在频谱域中提取热核特征描述符,揭示模型的稳定形状特征,进而结合模型表面局部体积特征的显著性与区分性,建立特征矩阵。最终通过特征矩阵的相似性度量与最短路径搜索,实现模型的相似性分析。通过实验可知,本文方法不仅能够高效地实现模型的对应性与相似性分析,而且可以揭示同类模型的统一结构特性,可以应用于三维模型的协同分割与检索研究。
1 热核 1.1 热核特征热核来源于黎曼流形上的热扩散理论,给定一个带有边界的紧致黎曼流形M,通过热传导方程来描述该流形上的某一区域随时间推移热量的变化,在数学上使用一个偏微分方程来表示。即:
| $ {\Delta _M}u\left( {x, t} \right) =-{\partial _{u\left( {x, t} \right)}}/{\partial _t} $ | (1) |
其中,ΔM为黎曼流形M的Laplace-Beltrami算子[18]。对于M有边界的情况,应使得u满足Dirichlet边界条件,即对于流形M上所有点x以及所有时间t,均满足u(x, t)=0。给定一个初始热源f,热传导方程在时间t上的解可以通过热算子Ht来得到,即为:
| $u\left( {x, t} \right) = {H_t}f$ | (2) |
对于任意流形M,存在函数kt(x, y):R+×M×M→R使得:
| $u\left( {x, t} \right) = \int_M {{k_t}\left( {x, y} \right)f\left( y \right){\rm{d}}y} $ | (3) |
满足式(3) 的最小值kt(x, y)称为热核,它可以看作经过时间t后点x处单位热量传递到点y的热量的总和。热核是热传导方程在适当边界条件下某一区域内的基础解,它也是数学物理中Laplace算子谱分析的重要工具, 其特征分解形式如下:
| ${k_t}\left( {x, y} \right) = \sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}} {\phi _i}\left( x \right){\phi _i}\left( y \right)$ | (4) |
其中:λM=[λ0, λ1, …, λi, …, λn]T是Laplace-Beltrami算子的特征值; ϕM=[ϕ0, ϕ1, …, ϕi, …, ϕn]T是对应的特征向量,并且满足ΔMϕi=λiϕi。热核函数kt(x, y)具有多种特性,与Laplace-Beltrami算子类似具有流形上的内蕴属性,具有等距等容不变性、多尺度特性以及在噪声微扰下具有稳定性。
Sun等[19]提出了热核特征(Heat Kernel Signature, HKS),抛弃了原有热核的空间尺度变量,将热核函数的变量限制在时域尺度内,并对时间尺度进行参数化采样,可以得到模型上每个点的热核特征表示:
| $\left\{ \begin{array}{l} HKS\left( x \right):{\boldsymbol{\rm{R}}^ + } \to \boldsymbol{\rm{R}}\\ HK{S_t} = {k_t}\left( {x, x} \right) = \sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\phi _i}{{\left( x \right)}^2}} \end{array} \right.$ | (5) |
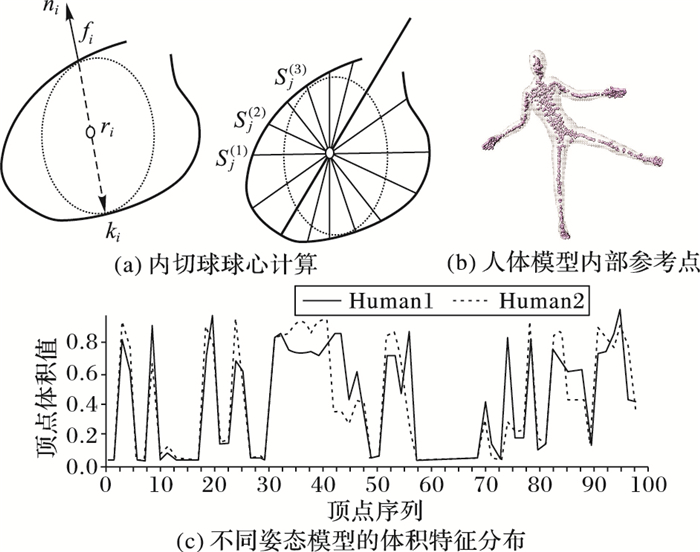
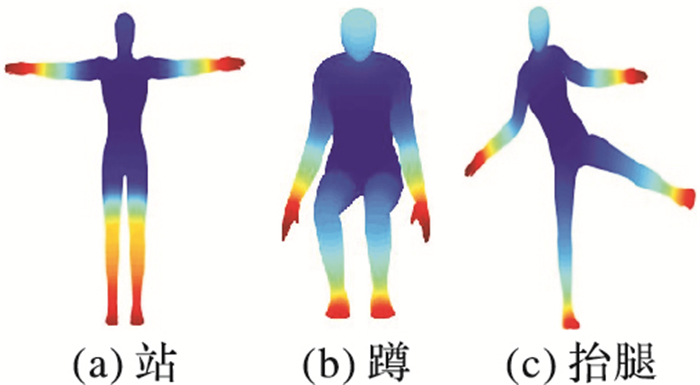
热核特征通过记录经过一段时间后点x的热量扩散到其他点来获取模型上该点的邻域内的几何信息。显然,时间t与扩散范围有关,可以获取模型多尺度的几何属性。某一t时刻不同姿态模型上的热核值的分布情况如图 1所示。由图 1可知,在不同姿态的同类模型中热核具有稳定的形状描述能力,因此可以作为三维模型点的特征描述符。
|
图 1 在同一t时刻,不同人体姿态模型上的热核分布 Figure 1 Heat kernel distribution on different human posture models at the same time of t |
给定时间t,St(x, y)为顶点(x, y)之间的扩散距离。这个距离一方面反映了(x, y)之间局部的结构,更重要的是它从宏观上给出了(x, y)之间的联系,这个距离St(x, y)包括了所有连接(x, y)之间路径的信息。扩散距离的关键在于它是基于扩散图上的多条路径,因此相比测地距离,扩散距离对噪声更具有鲁棒性,尤其对于不同姿态的模型间具有极强的稳定性[17]。
| $ \begin{array}{l} S{}_t\left( {x, y} \right) = k\left( x \right)-k\left( y \right) = \\ \;\;\;{\left( {\sum\limits_{i = 1}^{n-1} {{{\rm{e}}^{-\lambda _l^t}}{{\left( {{\phi _i}\left( x \right) - {\phi _i}\left( y \right)} \right)}^2}} } \right)^{1/2}} \end{array} $ | (6) |
其中:ϕ0是一个常量,ϕ1, ϕ2, …递减趋向于零。这个映射将原数据集映射到一个高维的数据空间,而在此空间中的欧氏距离直接等于它的扩散距离,这就为计算带来很大的方便。
模型的热扩散距离具有等距不变性且对于干扰具有稳定性,能够很好地描述模型的内蕴结构特征。如图 2所示,针对不同姿态的人体模型,提取热核特征,并依据扩散距离及K-means聚类方法实现模型的分割。由图 2可知,对于不同姿态的同类模型,可获得统一的分割结果,具有突出的形状稳定性与区分性。

|
图 2 基于扩散距离的模型分割(k=5) Figure 2 Model segmentation based on diffusion distance (k=5) |
由于热核具有等距不变性,能够很好地描述模型的内蕴结构特征,本文引入热核函数构造模型的特征矩阵,两个模型的相似性计算即转换为两个特征矩阵的相似性度量。
假设模型X和Y分别由热核特征表示,特征向量集构成了一个完全正交基,所有的基部{ϕk}k≥1构成模型X,同理,所有的基部{φk}k≥1构成了模型Y。
这样对任意的I:X→R与Q:Y→R,可以通过热核基构造特征矩阵I、Q:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{I}} = \sum\limits_{k \ge 1} {{a_k}{\mathit{\boldsymbol{\phi }}_k}} \\ \mathit{\boldsymbol{Q}} = \sum\limits_{k \ge 1} {{b_k}{\mathit{\boldsymbol{\varphi }}_k}} \end{array} \right. $ | (7) |
其中:I为m×k矩阵;Q为n×k矩阵;m、n分别为模型X和Y的顶点个数;k为所取的特征值个数。
常用的特征矩阵匹配方法是动态规划(Dynamic Programming, DP)匹配,是一种用来计算两个一维向量匹配距离的方法。它允许特征向量中的一个元素可以在给定的整合窗内选择对应特征向量中具有最小元素距离的元素作为其匹配对象, 而不仅仅限定在对应位置元素。
设定两个一维特征向量Ia=(Ia0, Ia1, …, Iai)和Qb=(Qb0, Qb1, …, Qbj),其元素匹配距离定义为:
| $ d\left( {{I_{ai}}, {Q_{bj}}} \right){\rm{ = }}\left| {{I_{ai}}-{Q_{bj}}} \right|/\left( {{I_{ai}} + {Q_{bj}}} \right) $ | (8) |
后文将d(Iai, Qbj)简写记为d(i, j),i=1, 2, …, m,j=1, 2, …, n。
特征向量Ia和Qb的m×n匹配距离计算矩阵如表 1所示。
| 表 1 m×n匹配距离计算矩阵 Table 1 Matching distance calculation matrix of m×n |
两个模型可通过计算匹配矩阵、判别其每一行的最小值计算模型间的最优匹配对。
| $ \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{\rm{arg}}\;{\rm{min}}\left( {d\left( {i{\rm{, }}j} \right)} \right)} } $ |
本文引入DP算法以及热核特征矩阵,计算模型的匹配距离,即模型上的热扩散距离。在每行中提取最小匹配距离,从而获得模型间最优的匹配对。
然而,由于热核特征无法有效地识别模型的局部细节特征,所以很难准确获得模型的对应关系。因此,本文在矩阵匹配中引入了可视体积进行约束。
2.2 基于体积的特征矩阵相似性计算空间体积特征通过衡量模型的内切球体积获得模型的局部形状描述,模型的局部空间体积对于模型的噪声及姿态变化具有极强的鲁棒性,而且能够有效识别模型的组成结构,被广泛应用于模型分割、检索应用中[20-21]。因此,在内蕴特征匹配距离基础之上,融合模型的局部体积特征约束,实现模型的匹配优化。
为了计算模型每个顶点的可视化体积,引入了高斯核函数来突出局部空间特征,首先以模型的内切球球心作为参考点,将参考点发出的射线进行去噪处理,保证射线分布的局部收敛性(如图 3(a)所示)。其次,通过计算射线与模型表面的距离lj获得模型每个顶点的局部体积值Vi[20]。
| $ \left\{ \begin{array}{l} {t_j} = {{\rm{e}}^{-\left( {{l_j}-u} \right)/\left( {2{\sigma ^2}} \right)}}\\ {V_i} = \sum\limits_{t = 1}^m {{l_j}} \cdot {t_j}/\sum\limits_{j = 1}^m {{t_j}} \end{array} \right. $ | (9) |
其中:u是线段li的平均值;σ是标准差。
图 4为基于模型间的空间体积特征并结合K-means方法进行模型分割的结果,可见其对于不同姿态的模型具有更为稳定的描述性,能够很好地识别模型的结构特征。

|
图 4 基于体积特征的形状分割 Figure 4 Shape segmentation based on volume signature |
将每个顶点对应的体积作为权值约束Wi,结合匹配点对之间的匹配距离进行优化,得到模型间精确的匹配关系。
| $ D\left( {i, j} \right) = \alpha V\left( {i, j} \right) + \beta d\left( {i, j} \right) $ | (10) |
其中:V(i, j)=V(i)-V(j)为两个顶点(i, j)间的体积差异度;d(i, j)为两个顶点间的扩散距离;α、β为权值系数。实验中,设置α=0.58、β=0.42,实现体积特征与热核特征的有效融合。
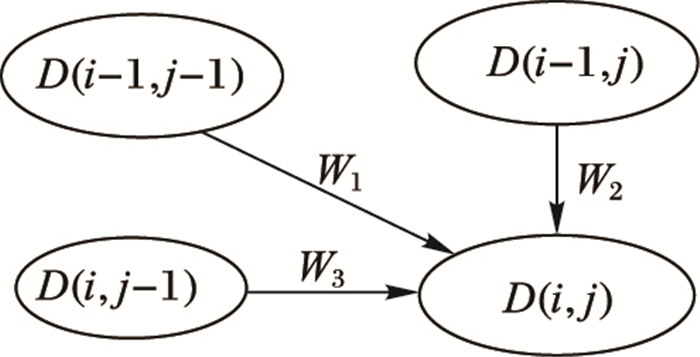
融合体积与热核特征的匹配矩阵如图 5所示,可视为一个有向加权图。从顶点D(i-1, j-1)、D(i-1, j)、D(i, j-1) 到D(i, j)分别连接一条有向边代表两个顶点的距离差值,这三条有向边的权值依次设定为W1、W2和W3,从中选择最小的权值边作为匹配边。这样,两个模型的匹配距离就是从D(1, 1) 到D(m, n)的一条最短路径上所有元素距离的和,即两个模型的匹配值。具体算法如下:
|
图 5 融合体积与热核特征的匹配矩阵 Figure 5 Matching matrix of the fusion with volume and heat kernel signature |
输入 模型M1与M2;
输出 匹配点对Π(xi, yj)以及模型的匹配值γ。
1) 建立模型M1与M2的邻接图表示:G1=(V1, E1),G2=(V2, E2)。
2) 计算模型上点的热核特征k(xi)|xi∈M1、k(yj)|yj∈M2,体积特征V(xi)、V(yj)。
3) 基于扩散距离计算特征匹配矩阵d。
4) 计算融合体积与热核特征的匹配矩阵D。
5) 循环检测,每行中最小距离点对Π(xi, yj)。
6) 输出模型的最小匹配路径,计算模型的匹配值γ。
热扩散距离的计算中,对于每一个模型,计算300个特征值和特征向量,t的选择在对数尺度时间区间[19]:tmin=4ln10/λ300, tmax=4ln10/λ2。
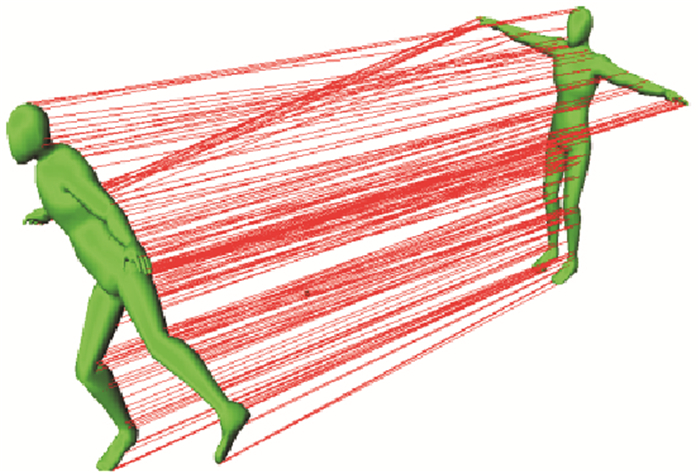
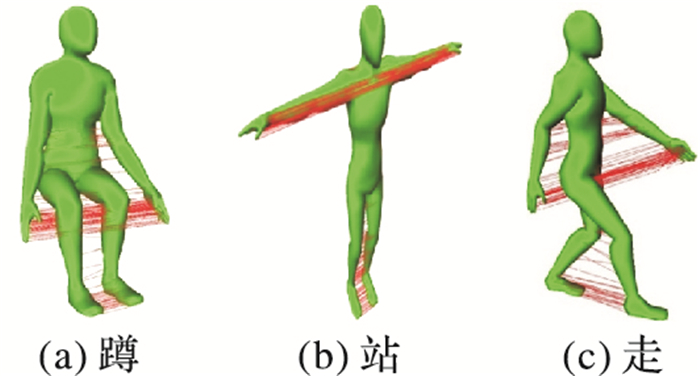
依据本文方法实现两组不同姿态人体模型的对应性匹配,如图 6所示,其在不同姿态变化的模型上可实现精准的对应性分析,具有较强的稳定性。
|
图 6 不同姿态模型的对应性分析 Figure 6 Correspondence analysis of different posture models |
算法实现平台为Core(TM) i5-3470 3.2 GHz CPU,8 GB内存的PC,并使用了VC++和Open Inventor图形库作为可视化开发环境。
采用了150个不同姿态的三维人体模型进行了实验验证。算法主要过程包括三步:1) 三维模型的热扩散距离与空间体积特征的计算;2) 基于融合特征的矩阵相似性度量;3) 最短路径及最小匹配搜索。实验中,依据文献[1]中多分辨率Reeb图(Multiresolutional Reeb Graph, MRG)的基本点分布原则,以基本点的半径作为邻域距离约束
| 表 2 本文方法的执行效率分析 Table 2 Execution efficiency analysis of the proposed method |
本方法首先建立三维模型的图表示,令无向带权图G(V, E)表示三维模型M,eij∈E表示连接相邻网格面片中心的边,pi∈V、pj∈V分别表示相邻网格面片的中心;进而利用图表示与Dijkstra最短路径算法,计算点对之间的测地线距离,构造模型的形状相似矩阵A。其时间复杂度为O(n log n),n为图表示中的顶点数目。利用形状相似矩阵与谱图分析方法,计算拉普拉斯算子,获得模型的热核特征,其算法时间主要取决于特征分解的时间,为O(n2)。
在求解模型的空间体积过程中,需要计算每个顶点的内切球,并计算射线与模型的交点,因此其计算时间为O(mn2), 其中m为发射的射线数目(m远小于n)。在模型匹配中,采取线性搜索方式,所以本文算法的总体实践复杂度为O(n2)。无论是点云模型、多边形网格还是多亏格表示,都可使用现有的技术构建三角网格,进行图的表示以及相似矩阵计算,所以本文方法具有广泛的适用性。
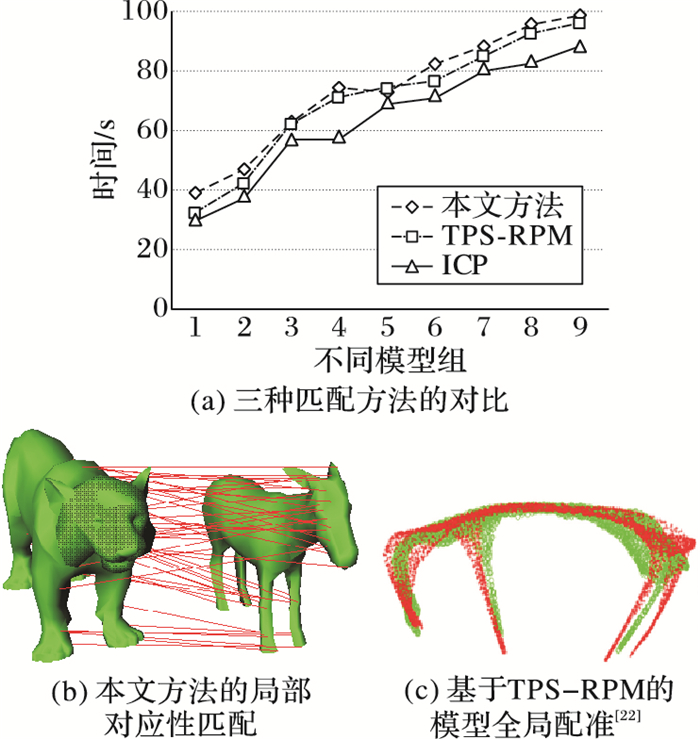
实验中,将本文方法与常用的ICP算法及TPS-RPM算法进行了形状配准对比分析,如图 7所示。ICP算法是通过就近点之间的最小距离来约束模型的配准过程,其要求配准的模型具有极高的相似性,而对于非相似的模型会出现极大的误差。同时,该方法只能实现刚性配准,对于具有不同姿态及局部形变的同类模型会产生巨大的差异。TPS-RPM算法通过优化薄板样条的光滑参数实现模型谱特征的非刚性配准,这使得模型即使谱特征差别很大的情况下也能进行配准并进行相似性分析,但其对于非线性的特征提取有一定的局限性,而且需要退火算法,迭代时间的选取是个难点。而本文算法结合了热扩散距离的稳定性与局部体特征的显著性,有效揭示了模型的内蕴形状特征,即使在模型表面形态出现很大偏差的情况下,如行走和下蹲的人体模型,均可实现模型的统一识别与形状匹配,对于不同的四肢模型(虎、驴)也可有效地获取局部匹配的特征点对。图 8及表 2进一步验证了本文方法的效率与精度。
|
图 7 不同方法的匹配分析 Figure 7 Matching analysis of different methods |
|
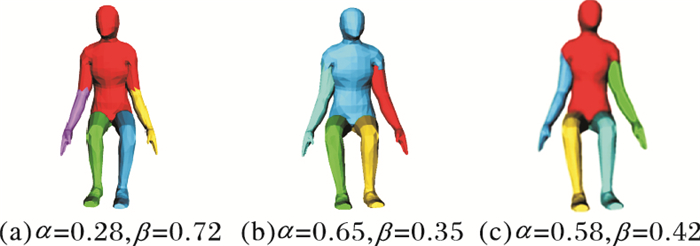
图 8 基于不同权值融合的形状分割结果 Figure 8 Shape segmentation results based on different weighting fusion |
实验中,关于特征融合权值α、β的设置,针对不同的模型进行了多次验证。使用不同设置获得的形状描述进行分割的结果如图 8所示。当热核特征与体积特征设置比例约为5:4,对于多数模型可获得较好的形状描述。
本文方法亦可应用于模型的自对称性检测,如图 9所示,输入模型M,通过分析模型本身的扩散距离以及局部体积约束,可有效识别具有相似形状特征的对称点,从而实现模型的内蕴自对称检测,可有效应用于模型的压缩、检索中。
|
图 9 模型的内蕴自对称检测 Figure 9 Self-symmetric detection of the models |
本文提出了融合热核特征与局部体积特征的三维模型对应分析方法,有效改进了频谱分析中形状匹配的稳定性与精度。通过引入模型内蕴结构特征以及空间体积的特征矩阵性相似性度量,有效地识别非刚性变形模型的形状相似性,降低了噪声和姿态对形状匹配的影响。
本文方法突出了模型的内蕴形状特征;同时,引入稳定的空间体积特征,突出了模型的几何局部细节。本文方法在执行效率与匹配精度上相比较使用传统ICP算法以及使用TPS-RPM算法形状配准方法有了一定的提高与改善。而且,本文方法可以有效地分析模型的对称特性,可以进一步应用于实现模型的简化、压缩、检索、协同分析等。在接下来的工作中,将基于现有的研究进一步探索群组模型的稀疏化表示与协同分析方法。
| [1] | HILAGA M, SHINAGAWA Y, KOMURA T, et al. Topology matching for fully automatic similarity estimation of 3D shapes[C]//SIGGRAPH'01:Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques. New York:ACM, 2001:203-212. |
| [2] | TIERNEY J, VANDEBORRE J P, DAOUDI M. Partial 3D shape retrieval by Reeb pattern unfolding[J]. Computer Graphics Forum, 2009, 28(1): 41-55. doi: 10.1111/cgf.2009.28.issue-1 |
| [3] | ZHENG Q, SHARF A, TAGLIASACCHI A, et al. Consensus skeleton for non-rigid space-time registration[J]. Computer Graphics Forum, 2010, 29(2): 635-644. doi: 10.1111/j.1467-8659.2009.01633.x |
| [4] | BARRA V, BIASOTTI S. 3D shape retrieval and classification using multiple kernel learning on extended Reeb graphs[J]. The Visual Computer, 2014, 30(11): 1247-1259. doi: 10.1007/s00371-014-0926-5 |
| [5] | CHEN Y, MEDIONI G. Object modeling by registration of multiple range image[J]. Image and Vision Computing, 1992, 10(3): 145-155. doi: 10.1016/0262-8856(92)90066-C |
| [6] | GELFAND N, IKEMOTO L, RUSINKIEWICZ S, et al. Geometrically stable sampling for the ICP algorithm[C]//3DIM 2003:Proceedings of the 2003 4th International Conference on 3D Digital Imaging and Modeling. Piscataway, NJ:IEEE, 2003:260-267. |
| [7] | DONATO G, BELONGIE S. Approximate thin plate spline mappings[C]//Proceedings of the 7th European Conference on Computer Vision, LNCS 2352. Berlin:Springer, 2002:21-31. |
| [8] | CHUI H, RANGARAJAN A. A new algorithm for non-rigid point matching[C]//Proceedings of the 2000 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC:IEEE Computer Society, 2000:44-51. |
| [9] | BOOKSTEIN F L. Principal Warps:thin-plate splines and the decomposition of deformations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6): 567-585. doi: 10.1109/34.24792 |
| [10] | MARTINEK M, GROSSO R, GREINER G. Interactive partial 3D shape matching with geometric distance optimization[J]. The Visual Computer, 2015, 31(2): 223-233. doi: 10.1007/s00371-014-1040-4 |
| [11] | RODOLÀE, COSMO L, BRONSTEIN M M, et al. Partial functional correspondence[J]. Computer Graphics Forum, 2015, 36(1): 222-236. |
| [12] | POKRASS J, BRONSTEIN A M, BRONSTEIN M M, et al. sparse modeling of intrinsic correspondences[J]. Computer Graphics Forum, 2014, 32(2): 459-468. |
| [13] | JAIN V, ZHANG H. Robust 3D shape correspondence in the spectral domain[C]//Proceedings of the 2006 IEEE International Conference on Shape Modeling and Applications. Washington. DC:IEEE Computer Society, 2006:1-19. |
| [14] | GLIKLIKH Y E. Global and Stochastic Analysis with Applications to Mathematical Physics[M]. London: Springer, 2011 : 139 -168. |
| [15] | COIFMAN R R, LAFON S. Diffusion maps[J]. Applied and Computational Harmonic Analysis, 2006, 21(1): 5-30. doi: 10.1016/j.acha.2006.04.006 |
| [16] | OVSJANIKOV M, SUN J, GUIBAS L. Global intrinsic symmetries of shapes[J]. Computer Graphics Forum, 2008, 27(5): 1341-1348. doi: 10.1111/cgf.2008.27.issue-5 |
| [17] | POKRASS J, BRONSTEIN A M, BRONSTEIN M M. Partial shape matching without point-wise correspondence[J]. Numerical Mathematics:Theory, Methods and Applications, 2013, 6(1): 223-244. |
| [18] | BELKIN M, SUN J, WANG Y S. Discrete Laplace operator on meshed surfaces[C]//SCG'08:Proceedings of 2008 24th Annual Symposium on Computational Geometry. New York:ACM, 2008:278-287. |
| [19] | SUN J, OVSJANIKOV M, GUIBAS L. A concise and provably informative multi-scale signature based on heat diffusion[J]. Computer Graphics Forum, 2009, 28(5): 1383-1392. doi: 10.1111/cgf.2009.28.issue-5 |
| [20] | 韩丽, 徐建国, 黎琳, 等. 基于表面及空间体积特征的人体模型结构分析[J]. 模式识别与人工智能, 2015, 28(3): 231-238. ( HAN L, XU J G, LI L, et al. Structure analysis for human models based on surface and spatial features[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(3): 231-238. ) |
| [21] | LIU R, ZHANG H, SHAMIR A, et al. A part-aware surface metric for shape analysis[J]. Computer Graphics Forum, 2009, 28(2): 397-406. doi: 10.1111/cgf.2009.28.issue-2 |
| [22] | 韩丽, 颜震, 徐建国, 等. 基于显著特征谱嵌入的三维模型相似性分析[J]. 模式识别与人工智能, 2015, 28(12): 1119-1126. ( HAN L, YAN Z, XU J G, et al. Three-dimensional model similarity analysis based on salient features spectral embedding[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(12): 1119-1126. ) |
| [23] | ZINBER T, SCHMIDT J, NIEMANN H. A refined ICP algorithm for robust 3D correspondence estimation[C]//Proceedings of the 2003 International Conference on Image Processing. Piscataway, NJ:IEEE, 2003:695-698. |
| [24] | SHAPIRA L, SHAMIR A, COHEN-OR D. Consistent mesh partitioning and skeletonisation using shape diameter function[J]. The Visual Computer, 2008, 24(4): 249-259. doi: 10.1007/s00371-007-0197-5 |
| [25] | KAZHDAN M, CHAZELLE B, DOBKIN D, et al. A reflective symmetry descriptor for 3D models[J]. Algorithmica, 2003, 38(1): 201-225. |
| [26] | KIM V, LIPMAN Y, CHEN X, et al. Mobius transformations for global intrinsic symmetry analysis[J]. Computer Graphics Forum, 2010, 29(5): 1689-1700. doi: 10.1111/cgf.2010.29.issue-5 |
| [27] | LIPMAN Y, FUNKHOUSER T A. Mobius voting for surface correspondence[J]. ACM Transactions on Graphics, 2009, 28(3): 1-12. |
| [28] | SIPIRAN I, GREGOR R, SCHRECK T. Approximate symmetry detection in partial 3D meshes[J]. Computer Graphics Forum, 2014, 33(7): 131-140. doi: 10.1111/cgf.2014.33.issue-7 |