2. 金陵科技学院 网络与通信工程学院, 南京 211169
2. College of Network and Communication Engineering, Science and Engineering, Jinling Institute of Technology, Nanjing Jiangsu 211169, China
随着对大容量和高质量的多媒体服务需求的增长,无线通信系统必须满足链路高负载以及频谱资源高利用率的要求。终端直通 (Device-to-Device, D2D) 通信技术可以在频谱资源有限的条件下潜在提高蜂窝系统吞吐量,并达到高速率传输的要求[1]。在蜂窝系统中引入D2D用户必然会带来干扰以及资源复用的问题,文献[2]指出了在蜂窝小区下进行D2D通信的挑战与收益。文献[3]提出了集中式功率控制策略,通过减少D2D带来的干扰保证蜂窝用户的有效覆盖概率,并提出分布式开关功率控制策略来最大化和速率。文献[4]介绍了正交与非正交资源共享模式下的蜂窝用户与D2D通信进行功率控制与资源分配,得到功率闭式解与最佳资源分配方案。同时,公平性的保证作为无线通信的另一研究课题必然存在于D2D系统,比例公平算法是目前最常用来保证公平性的一种调度算法,但在D2D通信中如果该算法设计不合理[5],便会陷入无限循环或连续调度一个用户,从而影响系统的公平性。文献[6-7]提出一种比例公平调度算法用于在多载波频分多址系统来分配上行链路资源,从而提升总的系统容量以及降低功率峰均比。文献[8]提出一种通过动态调整资源专用区与复用的界限的资源分配调度算法来保证公平性,并确定了比例公平的度量标准。
为了获得用户通信的公平性同时兼顾系统吞吐量,本文首先介绍了比例公平的原则,并将系统保证比例公平的问题转化为一个与加权和速率有关的问题,然后通过功率控制以及信道资源分配方案最大化系统总的加权和速率。仿真结果表明该方案能有效保证系统的公平性并能获得较高吞吐量。
1 比例公平准则比例公平调度准则的基本思想是在选择用户时考虑瞬时速率和长期平均速率的比值,从而达到系统吞吐量和公平性的最佳平衡。根据比例公平调度准则的定义[9-10],在含有i个用户的网络中,对任意可行的其他调度算法S,若经调度算法P调度的用户平均速率RiP满足:
| $\mathop \sum \limits_i {\mkern 1mu} \frac{{R_i^S - R_i^P}}{{R_i^P}}<0$ | (1) |
则调度算法P是比例公平的。其中RiS是用户i通过调度算法S调度过的平均速率。将式 (1) 转化可得:
| $\mathop \sum \limits_i {\mkern 1mu} \frac{{R_i^S - R_i^P}}{{R_i^P}} = \mathop \sum \limits_i {\mkern 1mu} {\rm{ }}{\left( {\ln R_i^P + c} \right)^\prime }\left( {R_i^S - R_i^P} \right) < 0$ | (2) |
其中c是个常量,令
| $f\left( {R_i^P} \right) - f\left( {R_i^S} \right) \ge \nabla f\left( {R_i^P} \right)\left( {R_i^P - R_i^S} \right)$ | (3) |
| $\nabla f\left( {R_i^P} \right)\left( {R_i^P - R_i^S} \right) = \mathop \sum \limits_i {\left( {{\rm{ln}}R_i^P + c} \right)^\prime }\left( {R_i^P - R_i^S} \right)$ | (4) |
联立式 (2)~(4) 可得:
| $f\left( {R_i^P} \right) \ge f\left( {R_i^S} \right)$ | (5) |
根据凸函数的性质,局部最优解也是全局最优解,所以,系统比例公平可以转化为最优化问题
| ${\rm{max}}\left\{ {\sum\limits_i {{\rm{ln}}{R_i}} } \right\}$ | (6) |
比例公平是个长期性的性能指标,根据比例公平调度,系统平均速率的更新是将瞬时速率经过指数加权的低通时间窗进行平均,即在调度时隙t用户的平均速率可写成:
| ${R_i}\left( t \right) = \left( {1 - \rho } \right){R_i}\left( {t - 1} \right) + \rho {r_i}\left( t \right)$ | (7) |
其中: ri(t) 是用户i在t时刻的瞬时速率;Ri(t) 是用户i在t时刻的长期平均速率;ρ是个遗忘因子,且ρ很小趋于零。令x=Ri(t), x0=Ri(t-1),将其代入式 (7) 中可得x-x0=ρ[ri(t)-Ri(t-1)], 根据一阶泰勒公式展开可得:
| $\ln {R_i}\left( t \right) = \ln {R_i}\left( {t - 1} \right) + \frac{1}{{{R_i}\left( {t - 1} \right)}}\rho \left[{{r_i}\left( t \right)-{R_i}\left( {t-1} \right)} \right]$ | (8) |
由于Ri(t-1) 的大小与调度时隙t不相关,可将其看作常量,设
| ${\rm{max}}\left\{ {\sum\limits_i {{\alpha _i}{r_i}\left( t \right)} } \right\}$ | (9) |
考虑在一个采用上行链路通信的蜂窝小区系统内部署多个D2D用户和普通蜂窝用户 (Cellular User, CU),同时,D2D用户复用其中一个CU的链路资源进行通信,所有用户都有以信号-干扰噪声比 (Signal to Interference plus Noise Ratio, SINR) 为指标的服务质量 (Quality of Service, QoS) 要求,并且基站有所有链路的信道状态信息 (Channel State Information, CSI)。所有蜂窝用户中有N个活跃的普通蜂窝用户占用了系统全部N个正交信道,其余蜂窝用户等待资源来通信,并且蜂窝系统中引入了M对D2D通信用户,用C和D分别表示活跃的CU与D2D对的用户集合。
对于信道模型,除了基于距离的路径损耗外,还考虑了由多径传播引起的快衰落和阴影效应引起的慢衰落。所以,CU与基站 (Base Station, BS) 之间的信道增益可表示为:
| ${g_{i, B}} = K{\beta _{i, B}}{\xi _{i, B}}L_{i, B}^{{\rm{ - }}\tau }$ | (10) |
其中:K是由系统决定的常量, βi, B是服从指数分布的快衰落增益, ξi, B表示服从对数分布的慢衰落增益,而Li, Bτ表示路径损耗。当D2D用户复用上行链路资源时,用gi表示D2D收发端的信道增益。对于干扰链路,用hj, B表示D2D的发射端到基站的信道增益,hi, j表示CU用户到D2D用户接收端的信道增益。假设一个上行蜂窝链路与一个D2D对复用频谱资源,组成一个资源复用对 (Resource Sharing Pair, RSP),每个RSP都分配有一个子信道, 因此单位带宽下系统吞吐量 (总的用户数据速率) 为:
| $\sum\limits_{i \in C} {\left[{{\rm{lb}}\left( {1 + {\gamma _i}} \right) + {\rho _{i, j}}\mathop \sum \limits_{j \in D}^{} {\rm{lb}}\left( {1 + {\gamma _j}} \right)} \right]} $ | (11) |
当ρi, j =1时,表示当前第i个CU与第j个D2D复用链路资源,组成RSP;当ρi, j =0时,表示该CU独立通信。
由于要使系统达到比例公平,必须满足式 (8),对于单个CU或单个RSP即要满足:
| $\mathop {{\rm{max}}}\limits_{{\rho _{i, j}}} \left\{ {{\alpha _i}{r_i}\left( t \right) + {\rho _{i, j}}{\beta _j}{r_j}\left( t \right)} \right\}$ | (12) |
βj与αi类似,是D2D用户比例公平加权因子, 也是个只与调度前一时刻有关而且在调度时隙已知的常量。单个RSP的和速率包括了CU的数据速率和复用其链路的D2D用户的速率,所以单个RSP的加权和速率表达式为:
| ${r_{i, j}}\left( t \right) = {\alpha _i}{\rm{lb}}\left( {1 + {\gamma _i}} \right) + {\beta _j}{\rm{lb}}\left( {1 + {\gamma _j}} \right)$ | (13) |
对于通信的用户还要保证用户服务质量要求并满足最大发射功率的条件限制,由式 (9)、(12) 和 (13) 可知,要保证混合D2D通信的多用户系统的比例公平,该问题可建模为:
| $\mathop {\max }\limits_{{\rho _{i, j}}, {\gamma _i}, {\gamma _j}} \left\{ {\sum\limits_{i \in C} {\left[{{\alpha _i}\;{\rm{lb}}\left( {1 + {\gamma _i}} \right) + {\rho _{i, j}}\mathop \sum \limits_{j \in D}^{} {\beta _j}\;{\rm{lb}}\left( {1 + {\gamma _j}} \right)} \right]} } \right\}$ | (14) |
限制条件:
| ${\gamma _i} = \frac{{{P_i}{g_{i, B}}}}{{{\sigma ^2} + {\rho _{i, j}}{P_j}{h_{j, B}}}} \ge {\gamma _{\min, i}}, \forall i \in C$ | (15) |
| ${\gamma _j} = \frac{{{P_j}{g_j}}}{{{\sigma ^2} + {\rho _{i, j}}{P_i}{h_{i, j}}}} \ge {\gamma _{\min, j}}, \forall j \in D$ | (16) |
| $\mathop \sum \limits_{j{\rm{ = }}1}^M {\rho _{i, j}} \le 1, {\rho _{i, j}} \in \left\{ {0, 1} \right\}, \forall i \in C$ | (17) |
| $\mathop \sum \limits_{i{\rm{ = }}1}^N {\rho _{i, j}} \le 1, {\rho _{i, j}} \in \left\{ {0, 1} \right\}, \forall j \in D$ | (18) |
| $0 \le {P_i} \le {P_{\max, i}}, \forall i \in C$ | (19) |
| $0 \le {P_j} \le {P_{\max, j}}, \forall j \in D$ | (20) |
其中:Pi和Pj分别表示普通蜂窝用户CU和D2D对的发射功率;γi和γj表示CU和D2D接收端的SINR。限制条件 (15) 和 (16) 表示用户的接入条件,必须满足QoS要求,即CU和D2D的SINR要大于最小的要求值;条件 (17) 和 (18) 表示对于任意一个普通蜂窝用户最多只能与一个D2D链路复用上行链路资源,这样做是为了简化系统由于引入D2D通信而产生的复杂的干扰环境;条件 (19) 和 (20) 限制了CU和D2D的发射功率能小于最大发射功率。
3 加权和速率分步优化方案式 (14) 与式 (11) 非常相似,可以看成最大化求解所有CU和RSP的总的加权和速率。由于其含有多个变量,难以直接求解,故考虑将其分成独立的几个子问题分步解决:第一步,考虑D2D与CU接入系统的限制条件, 得到用户能进行复用资源通信的接入条件;第二步,考虑D2D对与CU能够一对一复用上行链路资源,按照最优功率控制的方法将其单个RSP的加权和速率最大化;第三步,考虑多D2D与多CU复用时,用图论中的KM (Kuhn-Munkras) 算法匹配D2D用户与CU,进行CU信道资源分配,使总的加权和速率的最大化。
3.1 限制接入条件由限制条件 (15) 和 (16) 可知,D2D对与CU可以复用链路资源通信, 但需要保证用户的服务质量,即CU和D2D通信接收端的SINR高于门限值,此时用户才能接入系统。如果D2D用户与CU独立通信,第i个CU以及第j个D2D对的能保证最小SINR的最小传输功率为Pmin, i=(γmin, iσ2)/gi,B,Pmin, j=(γmin, jσ2)/gj,所以限制条件 (15), (16) 可以表示为:
| $ \left\{ \begin{array}{l} {P_i} \ge {P_{{\rm{min}},i}} + {P_j}\frac{{{\gamma _{{\rm{min}},i}}{h_{j,B}}}}{{{g_{i,B}}}}\\ {P_i} \le \frac{{{g_j}}}{{{\gamma _{{\rm{min}},j}}{h_{i,j}}}}{P_{{\rm{min}},i}} + {P_j}\frac{{{g_j}}}{{{\gamma _{{\rm{min}},j}}{h_{i,j}}}} \end{array} \right. $ | (21) |
对式 (2) 求解,并结合发射功率限制条件 (19) 和 (20),可得CU与D2D用户接入条件:
| $ \left\{ {\begin{array}{*{20}{c}} {0 < \frac{{\left( {{g_j}{\gamma _{{\rm{min}}, i}} + {h_{j, B}}{\gamma _{{\rm{min}}, i}}{\gamma _{{\rm{min}}, j}}} \right){\sigma ^2}}}{{{g_{i, B}}{g_j}-{h_{j, B}}{h_{i, j}}{\gamma _{{\rm{min}}, i}}{\gamma _{{\rm{min}}, j}}}} < {P_{{\rm{max}}, i}}}\\ {0 < \frac{{\left( {{g_{i, B}}{\gamma _{{\rm{min}}, j}} + {h_{i, j}}{\gamma _{{\rm{min}}, i}}{\gamma _{{\rm{min}}, j}}} \right){\sigma ^2}}}{{{g_{i, B}}{g_j}-{h_{j, B}}{h_{i, j}}{\gamma _{{\rm{min}}, i}}{\gamma _{{\rm{min}}, j}}}} < {P_{{\rm{max}}, j}}} \end{array}} \right. $ | (22) |
当通信设备满足上述条件时,此时选取一个上行蜂窝链路与一个D2D对复用频谱资源,组成一个资源复用对 (RSP),并要求使其加权和速率最大化,即:
| $\mathop {{\rm{max}}}\limits_{{P_{i, }}{P_j}} \left\{ {{\alpha _i}\;{\rm{lb}}\left( {1 + \frac{{{P_i}{g_{i, B}}}}{{{\sigma ^2} + {P_j}{h_{j, B}}}}} \right) + {\beta _j}\;{\rm{lb}}\left( {1 + \frac{{{P_j}{g_j}}}{{{\sigma ^2} + {P_i}{h_{i, j}}}}} \right)} \right\}$ | (23) |
这个最优化问题就是要在D2D与CU的可接入域中找到一个功率对 (Pi*, Pj*) 得到加权和速率最大值,文献[11]证明了式 (23) 是个凸函数,并得到最佳功率的闭式解为:
| $ \begin{array}{l} \left( {P_i^*,P_j^*} \right) = \\ \left\{ \begin{array}{l} \left\{ {\left( {{P_{\max ,i}},{P_1}} \right),\left( {{P_{\max ,i}},{P_2}} \right)} \right\},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{P_{\max ,i}}{g_{i,B}}}}{{{\sigma ^2} + {P_{\max ,j}}{h_{j,B}}}} \le {\gamma _{i,\min }}\;\\ \left\{ {\left( {{P_3},{P_{\max ,j}}} \right),\left( {{P_4},{P_{\max ,j}}} \right)} \right\},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{P_{\max ,i}}{g_{i,B}}}}{{{\sigma ^2} + {P_{\max ,j}}{h_{j,B}}}} > {\gamma _{\min ,i}}\;{\rm{ 且 }}\frac{{{P_{\max ,j}}{g_j}}}{{{\sigma ^2} + {P_{\max ,i}}{h_{i,j}}}} \le {\gamma _{\min ,j}}\\ \left\{ {\left( {{P_{\max ,i}},{P_1}} \right),\left( {{P_{\max ,i}},{P_{\max ,j}}} \right),\left( {{P_4},{P_{\max ,j}}} \right)} \right\},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{P_{\max ,i}}{g_{i,B}}}}{{{\sigma ^2} + {P_{\max ,j}}{h_{j,B}}}} > {\gamma _{\min ,i}}\;{\rm{ 且 }}\frac{{{P_{\max ,j}}{g_j}}}{{{\sigma ^2} + {P_{\max ,i}}{h_{i,j}}}} > {\gamma _{\min ,j}} \end{array} \right. \end{array} $ | (24) |
其中
在第3.2节中本文考虑了一个D2D对与一个CU复用的情况,得到单个RSP的加权和速率最大值:
| ${r_{i, j, {\rm{max}}}} = {\alpha _i}\;{\rm{lb}}\left( {1 + \frac{{P_i^*{g_{i, B}}}}{{{\sigma ^2} + P_j^*{h_{j, B}}}}} \right) + {\beta _j}\;{\rm{lb}}\left( {1 + \frac{{P_j^*{g_j}}}{{{\sigma ^2} + P_i^*{h_{i, j}}}}} \right)$ | (25) |
当系统中含有多个D2D对与多个CU时,要求多个RSP总的加权和速率最大,由于每个CU用户可能独立通信也可能与D2D复用链路资源通信,即要为每个D2D用户按加权和速率最大的原则分配一个CU的链路资源,根据其特点,可以将其转化为二分图的最大加权匹配问题,将每个RSP的加权和速率作为二分图中对应的边的权值,最大化多个用户匹配时的总的加权和速率问题可采取KM算法求解。
综上,为了保证系统的比例公平,本文提出了一个结合功率控制与用户匹配的资源分配方案——KMPF (Kuhn-Munkras Proportional Fair) 资源分配算法,具体步骤如下:
步骤1 建立二分图匹配模型。将所有CU用户C={CU1, CU2, …, CUN}组成顶点集X,D2D用户D={D2D1, D2D2, …, D2DM}组成顶点集Y。为X集中的每个顶点分配一个顶标Lci,同理为Y集中顶点分配顶标Ldj。
步骤2 通过最佳功率控制得到RSP的最大加权和速率。
步骤3 初始化二分图每条边的权值。如果CU独立通信则边的权值为CU的加权速率,如果CU与D2D复用资源则边的权值为该RSP的加权和速率。
步骤4 为每个D2D用户分配复用的CU用户信道资源。采用KM算法进行多个RSP加权和速率最大的二分图匹配,具体步骤如下:
1) 初始化匹配子图为空。
2) 从X第1个顶点开始,从Y中挑选未匹配且权值最大的点进行搜索,寻找增广路。如果经过一个未匹配点,说明寻找成功,更新路径信息,匹配边数加1,停止搜索, 如果一直没有找到增广路,则不再从这个点开始搜索。
3) 把增广路径添加到匹配子图中。
4) 若未找到完备匹配则修改顶标值,该路径上的X顶点集为Z,Y顶点集为T,对所有在Z中的点及不在T中的点,计算差值d=min{Ldj+Lci-ri, j, max},从Z集中的X顶标中减去d,并将其加入到T集中的Y的顶标中。
5) 循环步骤3)~4),直到找到所有二分图边权满足Ldj+Lci=ri, j, max的相等子图的完备匹配,此时即完成了对每个D2D用户分配CU信道资源。
4 仿真与分析本章给出仿真结果并对其进行分析讨论。
根据系统模型,对于单小区蜂窝网络,小区的半径设为500 m,普通蜂窝用户与D2D用户在小区中随机分布,基站位于小区的中心,D2D用户收发端的距离限制在50 m之内。D2D用户与普通蜂窝用户的最大发射功率为24 dBm。系统带宽为5 MHz,信道模型的路径损耗因子τ=4,K=0.01,阴影衰落服从标准方差为8 dB的正态分布,不考虑其他因素的影响。
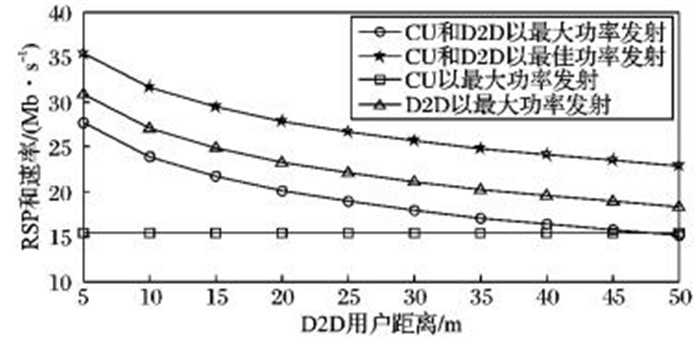
图 1是单个RSP经功率控制方案后得到的和速率变化曲线,可以看出,单独的D2D通信相比单独的CU通信由于其路径损耗小,数据速率在最大发射功率下要高约70%~130%。当CU与D2D复用资源通信时,RSP以最佳功率发射相比以最大功率发射的和速率提高了40%~60%,这是因为通过功率控制可以有效地协调用户之间的干扰,并且随着D2D用户距离的增加,其和速率逐渐变小。
|
图 1 不同发射功率下RSP的和速率比较 Figure 1 Comparison of sum-rate of RSP under different transmitting powers |
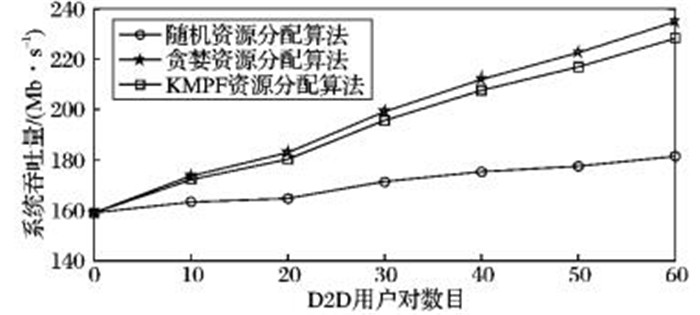
下面比较本文算法与文献[12]中的随机资源分配算法以及文献[13]中贪婪启发式资源分配算法对系统性能的影响。图 2是当系统中CU用户数目为100时,随着接入D2D用户数目增加,不同资源分配算法下系统吞吐量的变化趋势。可以看出,系统按照随机资源分配算法进行资源调度时,系统的吞吐量水平较低。在贪婪启发式资源分配算法调度下,由于优先给信道条件好且干扰增益小的用户分配资源,系统吞吐量提升较大,当复用资源的D2D通信用户对数目为60时,提升了约50%。一般来说,可以将贪婪算法进行资源调度的系统的吞吐量看作系统吞吐量的上界。本文所提出的KMPF资源分配,通过最佳功率控制进行和速率优化,并优先将资源分配给信道条件相对较好且长期平均吞吐量小的用户,可以使在每个调度周期内吞吐量达到贪婪算法调度95%。说明该资源分配算法能在调度周期 (短期) 内获得较大的系统吞吐量。
|
图 2 系统吞吐量比较 Figure 2 Comparison of system throughput |
为了衡量系统公平性,采用文献[14-15]中的Jain’s Index作为公平指数 (F),其表达式为:
| $ F = \frac{{{{\left[{\sum\limits_i^n {{R_i}(\Delta t)} } \right]}^2}}}{{n\sum\limits_i^n {{R_i}{{(\Delta t)}^2}} }} $ | (26) |
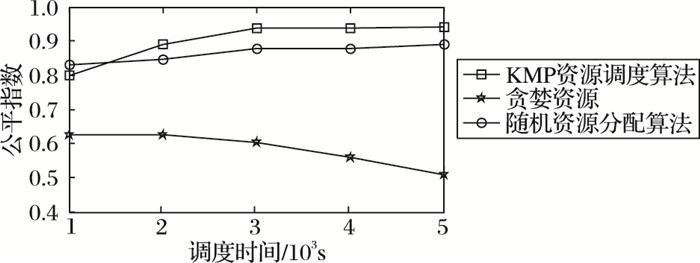
其中:n是系统中的用户数目,Ri(Δt) 是用户i在间隔时间Δt内的吞吐量。通过对用户吞吐量的公平指数的计算,来反映用户传输的数据量的差异,从而体现各用户之间通信的公平性。该公平指数越大,说明用户公平性越高。图 3表示当系统中有100个CU和40个D2D用户 (20个D2D用户对),每个调度周期为T =1 000 s,在经过不同的调度时间,不同资源分配算法调度下的系统的吞吐量公平指数变化趋势。可以看出,贪婪启发式算法的调度时间越长,由于调度用户分布集中,用户吞吐量差异越大,公平指数越低;当系统采用KMPF资源分配算法,随着调度时间延长,用户的平均吞吐量差异越小,经过3个调度周期 (T) 后达到了一个相对稳定的点,公平指数提升了约17%,且高于随机资源分配算法的公平指数,说明KMPF资源调度算法能使系统的长期公平性得到保证。
|
图 3 系统公平指数比较 Figure 3 Comparison of system fairness index |
通信系统中,通信公平性与最大化吞吐量是两个矛盾的课题。本文主要贡献是将系统公平性问题转化为最大化系统加权和速率的问题,然后将其引入D2D通信与蜂窝共存的系统中,根据提出的结合了功率控制以及最大化系统加权和速率的资源分配方案,获得系统的比例公平,在兼顾系统吞吐量的同时,有效解决了系统公平性问题。
| [1] | DOPPLER K, RINNE M, WIJTING C, et al. Device-to-device communication as an underlay to LTE-advanced networks[J]. IEEE Communications Magazine, 2009, 47(12): 42-49. doi: 10.1109/MCOM.2009.5350367 |
| [2] | FENG D, LU L, YUAN-WU Y, et al. Device-to-device communications in cellular networks[J]. IEEE Communications Magazine, 2014, 52(4): 49-55. doi: 10.1109/MCOM.2014.6807946 |
| [3] | YU C H, DOPPLER K, RIBEIRO C B, et al. Resource sharing optimization for device-to-device communication underlying cellular networks[J]. Wireless Communications, 2011, 10(8): 2752-2763. |
| [4] | LEE N, LIN X, ANDREWS J G, et al. Power control for D2D underlaid cellular networks:modeling, algorithms, and analysis[J]. IEEE Transactions on Selected Areas in Communications, 2015, 33(1): 1-13. doi: 10.1109/JSAC.2014.2369612 |
| [5] | BATISTA R L, E SILVA C F M, DA SILVA J M B, et al. What happens with a proportional fair cellular scheduling when D2D communications underlay a cellular network?[C]//Proceedings of the 2014 IEEE Wireless Communications and Networking Conference Workshops. Piscataway, NJ:IEEE, 2014:260-265. |
| [6] | SHAH S T, GU J, HASAN S F, et al. SC-FDMA-based resource allocation and power control scheme for D2D communication using LTE-A uplink resource[J]. EURASIP Journal on Wireless Communications and Networking, 2015, 2015(1): 1-15. |
| [7] | LEE J, GU J, BAE S J, et al. A resource allocation scheme for improving user fairness in device-to-device communication based on cellular networks[C]//Proceedings of the 7th International Conference on Ubiquitous Information Management and Communication. New York:ACM, 2013:Article No. 112. |
| [8] | WANG H H, CHEN J C, LIU Z N. Resource allocation in central-controlled device-to-device communications networks[C]//Proceedings of the 2013 IEEE Globecom Workshops. Piscataway, NJ:IEEE, 2013:4871-4876. |
| [9] | KELLY F P, MAULLOO A K, TAN D K H. Rate control for communication networks:shadow prices, proportional fairness and stability[J]. Journal of the Operational Research Society, 1998, 49(3): 237-252. doi: 10.1057/palgrave.jors.2600523 |
| [10] | NGUYEN T D, HAN Y. A proportional fairness algorithm with QoS provision in downlink OFDMA systems[J]. IEEE Communications Letters, 2006, 10(11): 760-762. doi: 10.1109/LCOMM.2006.060750 |
| [11] | FENG D, LU L, YUAN-WU Y, et al. Device-to-device communications underlying cellular networks[J]. IEEE Transactions on Communications, 2013, 61(8): 3541-3551. doi: 10.1109/TCOMM.2013.071013.120787 |
| [12] | SUN H, SHENG M, WANG X, et al. Resource allocation for maximizing the device-to-device communications underlaying LET-Advanced networks[C]//Proceedings of the 2013 IEEE/CIC International Conference on Communications in China-Workshops. Piscataway, NJ:IEEE, 2013:60-64. |
| [13] | ZULHASNINE M, HUANG C, SRINIVASAN A. Efficient resource allocation for device-to-device communication underlaying LTE network[C]//Proceedings of the 2010 IEEE 6th International Conference on Wireless and Mobile Computing, Networking and Communications. Piscataway, NJ:IEEE, 2010:368-375. |
| [14] | HARTAMAN A, RAHMAT B. Performance and fairness analysis (using Jain's index) of AODV and DSDV based on ACO in MANET[C]//Proceedings of the 20154th International Conference on Interactive Digital Media. Piscataway, NJ:IEEE, 2015:1-7. |
| [15] | JAIN R, CHIU D M, HAWE W R. A quantitative measure of fairness and discrimination for resource allocation in shared computer system[J/OL].[2016-06-20].https://arxiv.org/ftp/cs/papers/9809/9809099.pdf. |
| [16] | 于升升, 葛万成, 郭爱煌. 基于最大加权队列的终端到终端通信时延感知跨层设计算法[J]. 计算机应用, 2015, 35(5): 1205-1208. ( YU S S, GE W C, GUO A H. Delay-aware algorithm of cross-layer design for device-to-device communication based on max-weighted queue[J]. Journal of Computer Applications, 2015, 35(5): 1205-1208. doi: 10.11772/j.issn.1001-9081.2015.05.1205 ) |




