2. 国网安庆供电公司 安全监察质量部, 安徽 安庆 246000;
3. 安徽南瑞继远电网技术有限公司, 合肥 230088;
4. 安徽大学 电子信息工程学院, 合肥 230601
2. Safety Supervision Quality Department, State Grid Anqing Electric Power Supply Company, Anqing Anhui 246000, China;
3. Anhui Jiyuan Electric Power System Technology Company Limited, Hefei Anhui 230088, China;
4. School of Electronics and Information Engineering, Anhui University, Hefei Anhui 230601, China
提取高效且具有鉴别力的特征描述是人脸识别及其他模式识别应用中的一个关键问题, 特征提取质量的好坏将直接影响后继分类、识别的性能。特征提取的目标是在获得高效鉴别能力的同时尽可能增加特征的类内相似度并减小类间相似度。然而, 在人脸识别应用中由于表情、光照、姿势、遮挡等各种因素的影响, 高效、鲁棒的特征提取仍然是一个热点研究问题。
现有人脸特征描述方法总体上可分为整体特征提取和局部特征提取两大类。整体特征提取常用的方法有主成分分析 (Principal Components Analysis, PCA)[1]、线性判别分析 (Linear Discriminant Analysis, LDA)[2]、判别共同矢量 (Discriminant Common Vector, DCV)[3]、广义判别分析 (Generalized Discriminant Analysis, GDA)[4]、核判别共同矢量 (Kernel Discriminant Common Vector, KDCV)[5]等。PCA旨在寻找使全局特征样本向量方差最大化下的降维投影, 在保证重建误差最小的情况下把人脸图像向量从复杂的高维降到更容易区分的低维向量;LDA进一步利用了样本的标签信息, 寻找在扩大样本类间差异的同时又能缩小类内样本差异的降维投影;DCV算法在类内协方差矩阵的零空间内寻找判别共同矢量, 通过判别共同矢量组得到最优的投影矩阵对高维人脸样本向量进行降维特征提取;GDA和KDCV分别是对LDA和DCV在核空间的扩展, 其把原始向量向更高维空间进行非线性投影后再进行降维以提取更具鉴别力的特征。Gabor小波[6]和局部二值模式 (Local Binary Pattern, LBP)[7]是常见的局部特征描述子, 二者对于局部光照、表情变化以及图像的非精确对齐有较好的鲁棒性。Gabor小波可以获得不同尺度和方向下的局部特征结构, 对光照和表情变化都比较鲁棒;LBP用邻域各点灰度值与中心点相比较, 是简单有效的人脸特征描述方法。为了更好地提取局部特征, 在LBP的基础上又发展形成了多尺度分块局部二值模式 (Multi-scale Block LBP, MBLBP)[8]、局部Gabor二值模式 (Local GBP, LGBP)[9]、局部方向模式 (Local Direction Pattern, LDP)[10]等算法。
上述人脸特征描述均采用手工设计的特征描述子, 该类方法从主观的手动设计原则出发, 很难得到最优的编码方案。针对该问题, Lei等[11]于2012年提出了一种具有分类判别作用的可学习图像滤波器 (Image Filter Learning, IFL) 并将其与LBP结合在特征描述阶段就对人脸图像实现初步分类判别。随后, IFL又被应用到可学习人脸特征描述器 (Discriminant Face Descriptor, DFD)[12]上。IFL将Fisher判别准则与LBP算法融合, 在提取各张人脸图片特征的同时获取不同样本图片间的类别特征, 提高了滤波后图像的分类鉴别能力。可学习图像滤波器IFL不仅能使滤波后的人脸图像更具有鉴别力, 更重要的是其由训练集动态学习得来, 具有自适应性, 在不同的训练集上可针对性地获得最优滤波器参数。由于IFL直接在像素空间进行滤波器学习, 光照、表情、姿势等因素往往会造成人脸识别过程中的非线性问题, 而线性的IFL不能够更好地处理此类问题。此外, 为模拟LBP的邻域像素对比的思想, IFL在进行滤波器学习过程中仅利用了图像的一阶微分信息, 而图像中的角点、灰度变化率等高阶微分信息并未充分利用。
针对以上问题, 本文在IFL的基础上提出一种基于学习的核图像微分滤波器 (Kernel Image Differential Filter, KIDF)。该算法首先通过引入核运算将滤波器学习从像素空间转换到高维空间, 使得原本在低维空间中的线性不可分问题转化为在高维特征空间的线性可分问题; 其次, 为了更加充分利用人脸的丰富细节特征, 在滤波器学习时除一阶微分信息外还进一步考虑了图像的二阶微分信息。实验结果表明了本文方法的有效性。
1 基于学习的线性判别滤波器基于学习的线性判别滤波器 (IFL)[11]将传统LBP的邻域像素灰度比较思想推广至相邻的局部区域内各像素灰度按对应位置依次比较, 同时融合Fisher线性判别分析原理, 使滤波后样本集内属于同一分类下图像间像素差异程度减小, 且不同分类下的图像间像素差异程度扩大。
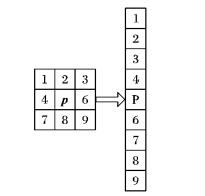
线性判别滤波器的滤波处理为逐像素进行。令p点为待滤波图像的一个像素点, 以p为中心的3×3局部图像块如图 1左侧所示。将该图像块按行拉成一列向量, 获得如图 1右侧所示的图像块向量。将图像块向量与滤波器向量做内积运算, 所得结果取代原p点像素值即可完成p点处的滤波。
|
图 1 图像块转为图像块向量 Figure 1 Converting image block to image block vector |
设训练集中包括C个人的共N个样本图像, Ni为第i个人的样本数。给定图像I, 令f(I) 为滤波后图像, 类似LBP的局部像素比较思想, p点处的像素差异向量可写为:
| $ \begin{align} & df{{(\mathit{\boldsymbol{I}})}^{\mathit{\boldsymbol{p}}}}=[f{{(\mathit{\boldsymbol{I}})}^{{{\mathit{\boldsymbol{p}}}_{1}}}}-f{{(\mathit{\boldsymbol{I}})}^{\mathit{\boldsymbol{p}}}}, f{{(\mathit{\boldsymbol{I}})}^{{{\mathit{\boldsymbol{p}}}_{2}}}}-f{{(\mathit{\boldsymbol{I}})}^{\mathit{\boldsymbol{p}}}}, \cdots, \\ & \ \ \ \ \ \ \ \ \ \ \ \ f{{(\mathit{\boldsymbol{I}})}^{{{\mathit{\boldsymbol{p}}}_{d}}}}-f{{(\mathit{\boldsymbol{I}})}^{\mathit{\boldsymbol{p}}}}] \\ \end{align} $ | (1) |
其中: f(I)p和f(I)pi分别表示f(I) 在p点和其第i个邻域点pi处的图像块向量。令f(I)ijp为第i个人第j个样本的滤波后图像在p点处的图像块向量, 假设每张图像有L个像素, 分别以每个像素为中心可获得L个像素差异向量, 将这些向量按列组合可获得像素差异矩阵:
| $ df{{(\mathit{\boldsymbol{I}})}_{ij}}=[df(\mathit{\boldsymbol{I}})_{ij}^{1}, df(\mathit{\boldsymbol{I}})_{ij}^{2}, \cdots, df(\mathit{\boldsymbol{I}})_{ij}^{L}] $ | (2) |
按照Fisher判别准则, 像素差异矩阵的类内和类间散度可分别写为:
| $ {{\mathit{\boldsymbol{S}}}_{\rm{w}}}=\sum\limits_{i=1}^{C}{\sum\limits_{j=1}^{{{N}_{i}}}{(df{{(\mathit{\boldsymbol{I}})}_{ij}}-\overline{df{{(\mathit{\boldsymbol{I}})}_{i}}})}}{{(df{{(\mathit{\boldsymbol{I}})}_{ij}}-\overline{df{{(\mathit{\boldsymbol{I}})}_{i}}})}^{\rm{T}}} $ | (3) |
| $ {{\mathit{\boldsymbol{S}}}_{\rm{b}}}=\sum\limits_{i=1}^{C}{{{N}_{i}}}(\overline{df{{(\mathit{\boldsymbol{I}})}_{i}}}-\overline{df(\mathit{\boldsymbol{I}})}){{(\overline{df{{(\mathit{\boldsymbol{I}})}_{i}}}-\overline{df(\mathit{\boldsymbol{I}})})}^{\rm{T}}} $ | (4) |
其中:
令待学习的图像滤波器向量为w, 有
| $ f{{(\mathit{\boldsymbol{I}})}^{\mathit{\boldsymbol{p}}}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{\mathit{\boldsymbol{I}}}^{\mathit{\boldsymbol{p}}}} $ | (5) |
| $ df{{(\mathit{\boldsymbol{I}})}_{ij}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}d{{\mathit{\boldsymbol{I}}}_{ij}} $ | (6) |
其中:dIij和df(I)ij分别为滤波前后第i个人的第j个样本的像素差异矩阵。式 (5) 表示图像I在像素p点处的滤波过程。将式 (6) 代入式 (3)、(4) 中可得:
| $ {{\mathit{\boldsymbol{S}}}_{\rm{w}}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}(\sum\limits_{i=1}^{C}{\sum\limits_{j=1}^{{{N}_{i}}}{(d{{\mathit{\boldsymbol{I}}}_{ij}}-\overline{{{\mathit{\boldsymbol{I}}}_{i}}})}}{{(d{{\mathit{\boldsymbol{I}}}_{ij}}-\overline{{{\mathit{\boldsymbol{I}}}_{i}}})}^{\rm{T}}})\mathit{\boldsymbol{w}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\hat{S}}}}}_{\rm{w}}}\mathit{\boldsymbol{w}} $ | (7) |
| $ {{\mathit{\boldsymbol{S}}}_{\rm{b}}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}(\sum\limits_{i=1}^{C}{{{N}_{i}}}(\overline{{{\mathit{\boldsymbol{I}}}_{i}}}-\overline{\mathit{\boldsymbol{I}}}){{(\overline{{{\mathit{\boldsymbol{I}}}_{i}}}-\overline{\mathit{\boldsymbol{I}}})}^{\rm{T}}})\mathit{\boldsymbol{w}}={{\mathit{\boldsymbol{w}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\hat{S}}}}}_{\rm{b}}}\mathit{\boldsymbol{w}} $ | (8) |
其中:I和
此时, 求自适应滤波器w即转化为求
线性判别滤波器使用图像块向量同滤波器向量的内积替换当前像素, 并直接在像素空间进行滤波器学习。而实际人脸识别中, 光照、表情、姿势等因素引入的非线性极大限制了线性判别滤波器的性能。此外, IFL中的滤波器向量是在像素差异矩阵的基础上学习获得, 像素差异矩阵本质上可看成是图像一阶微分信息集合, 而包含角点、灰度变化率等丰富细节的高阶微分信息并未得到充分利用。
为解决上述问题, 本文首先在IFL的基础上引入核运算。核运算[13]在解决非线性分类问题上的有效性已在很多应用中得以证明。核运算将低维特征映射到高维, 使得原本在低维空间中的线性不可分问题转化为在高维特征空间中的线性可分问题, 同时巧妙地运用了隐式投影在不显著增加计算量的前提下实现映射。其次, 不同于IFL利用像素差异矩阵隐式使用图像一阶微分信息, 本文提出在图像块向量构建时显式地引入图像一阶、二阶微分以及原始像素灰度信息, 这些丰富特征信息的引入将有助于学习更具鉴别力的滤波器。
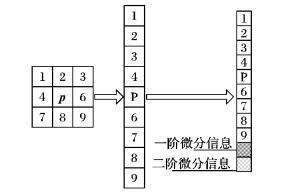
2.1 图像块向量的微分信息扩充由第1章可知, 线性判别滤波器中任意一点p对应的图像块向量由以p为中心的局部区域按行拉伸组成, 因此该图像块向量仅包含p的邻域像素信息。为进一步考虑邻域内的微分信息, 可在上述图像块向量的基础上进行维数扩充, 引入该像素点处的一阶和二阶微分信息 (如图 2所示)。
|
图 2 图像块向量的微分信息扩充 Figure 2 Differential information extension of image block vector |
假设p点坐标为 (i, j), 该点处沿x、y方向的一阶微分近似可由式 (9) 获得:
| $ \left\{\begin{align} & \frac{\partial \mathit{\boldsymbol{I}}(i, j)}{\partial x}=\mathit{\boldsymbol{I}}(i+1, j)-\mathit{\boldsymbol{I}}(i, j) \\ & \frac{\partial \mathit{\boldsymbol{I}}(i, j)}{\partial y}=\mathit{\boldsymbol{I}}(i, j+1)-\mathit{\boldsymbol{I}}(i, j) \\ \end{align} \right. $ | (9) |
该点处沿x、y方向的二阶微分近似由式 (10) 获得:
| $ \left\{\begin{align} & \frac{{{\partial }^{2}}\mathit{\boldsymbol{I}}(i, j)}{\partial {{x}^{2}}}=\mathit{\boldsymbol{I}}(i+1, j)-2\mathit{\boldsymbol{I}}(i, j)+\mathit{\boldsymbol{I}}(i-1, j) \\ & \frac{{{\partial }^{2}}\mathit{\boldsymbol{I}}(i, j)}{\partial {{y}^{2}}}=\mathit{\boldsymbol{I}}(i, j+1)-2\mathit{\boldsymbol{I}}(i, j)+\mathit{\boldsymbol{I}}(i, j-1) \\ \end{align} \right. $ | (10) |
其中:I(i, j) 为图像在坐标 (i, j) 处的亮度。
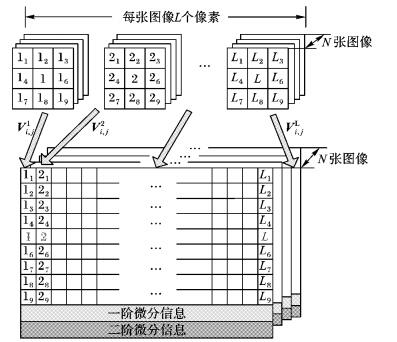
2.2 核图像微分滤波器学习令Iij为第i个人的第j个样本图像, Vijp为图像Iij在p点处的经过2.1节微分信息扩充后的图像块向量。如果Iij有L个待处理像素, 如图 3所示, 可将这L个像素的图像块向量拼合成图像块向量矩阵
|
图 3 图像块向量矩阵构建 Figure 3 Construction of image block matrix |
类似第1章中描述, 此时类内散布阵和类间散布阵分别表示为:
| $ {{\mathit{\boldsymbol{S}}}_{\rm{w}}}=\sum\limits_{i=1}^{C}{\sum\limits_{j=1}^{{{N}_{i}}}{({{\mathit{\boldsymbol{M}}}_{ij}}-{{\overline{\mathit{\boldsymbol{M}}}}_{i}})}}{{({{\mathit{\boldsymbol{M}}}_{ij}}-{{\overline{\mathit{\boldsymbol{M}}}}_{i}})}^{\rm{T}}} $ | (11) |
| $ {{\mathit{\boldsymbol{S}}}_{\rm{b}}}=\sum\limits_{i=1}^{C}{{{N}_{i}}}({{\mathit{\boldsymbol{M}}}_{i}}-\overline{\mathit{\boldsymbol{M}}}){{({{\mathit{\boldsymbol{M}}}_{i}}-\overline{\mathit{\boldsymbol{M}}})}^{\rm{T}}} $ | (12) |
其中:
为了解决特征的非线性问题, 引入核运算后式 (11) 和 (12) 可改写为:
| $ \varphi {{\mathit{\boldsymbol{S}}}_{\rm{w}}}=\sum\limits_{i=1}^{C}{\sum\limits_{j=1}^{{{N}_{i}}}{(\varphi {{\mathit{\boldsymbol{M}}}_{ij}}-\varphi {{\overline{\mathit{\boldsymbol{M}}}}_{i}})}}{{(\varphi {{\mathit{\boldsymbol{M}}}_{ij}}-\varphi {{\overline{\mathit{\boldsymbol{M}}}}_{i}})}^{\rm{T}}} $ | (13) |
| $ \varphi {{\mathit{\boldsymbol{S}}}_{\rm{b}}}=\sum\limits_{i=1}^{C}{{{N}_{i}}}(\varphi {{\mathit{\boldsymbol{M}}}_{i}}-\varphi \overline{\mathit{\boldsymbol{M}}}){{(\varphi {{\mathit{\boldsymbol{M}}}_{i}}-\varphi \overline{\mathit{\boldsymbol{M}}})}^{\rm{T}}} $ | (14) |
其中:带有前置符号φ的数据表示原样本空间中数据投影到高维空间下对应的高维数据。
此时使得 (φwTφSbφw)/(φwTφSwφw) 值最大的φw即为待求的高维空间中最优的滤波器向量。类似第1章中讨论, 求最优φw的问题可以转化为φSw-1φSb的特征值分解问题, 其最大特征值对应的特征向量即为最优φw, φwTφMi, j即为滤波后样本的图像块向量。
3 实验结果及分析为了验证本文算法的有效性, 实验在AR和ORL两个人脸数据库上进行, 并将本文算法同线性可学习图像滤波器IFL以及本文方法的一些变种方法, 即不考虑微分信息的核图像滤波器 (KIDF) 以及只考虑一阶微分信息的核图像滤波器 (KIDF (1)) 进行比较。为保证实验结果的客观性, 在实验中随机选取60%的样本图像进行训练, 剩下的40%进行测试, 并取30次随机测试识别率的均值作为最终结果参与比较。
3.1 直观比较实验图 4给出了两组人脸图像滤波前后效果的直观对比, 其中左侧为原始图像, 右侧为本文算法滤波后图像。可以看出, 原始图像中相同个体的两个样本图像均存在明显的姿态差异, 而经过滤波后相同个体不同样本间的差异明显缩小, 不同个体间的差异加大。该实验在直观上证实了本文算法在提取鉴别特征时增大类内相似度、减小类间相似度上的有效性。

|
图 4 基于学习的微分核图像滤波器的滤波效果 Figure 4 Results after applying learning based kernel image differential filter |
AR库共有100人, 每人14张图片。图 5给出该库中的部分样本图像, 可以看出AR库存在明显的光照和表情变化, 这些因素引入的特征非线性有利于验证本文结合核运算的图像滤波器的有效性。

|
图 5 AR库人脸样本图像 Figure 5 Sample images of AR dataset |
表 1中给出了本文算法同LBP和IFL在L1范数距离 (L1)、卡方检验 (χ2)、最近邻 (Nearest Neighbor, NN)、直方图相交 (Histogram Intersection, HI) 和支持向量机 (Support Vector Machine, SVM) 五种不同相似性度量下的识别率对比, 其中KIFL表示不考虑微分信息的核图像滤波器, 其仅在IFL算法基础上使用核空间扩展, KIDF (1) 表示只考虑一阶微分和核运算的算法。由于SVM在分类时也采用了核运算, 可以看出本文算法除在SVM分类器下识别率同IFL持平外, 在其余度量下均稳定地优于其他算法。
| 表 1 AR库识别率对比 Table 1 Comparison of recognition rate in AR dataset |
ORL库共有40人, 每人10张图片。表 2中给出了本文算法同其他算法的平均识别率对比。可以看出, 本文算法在不同度量方法下的识别率均优于其他算法, 这也说明了本文引入二阶微分和核运算的有效性。
| 表 2 ORL库识别率对比 Table 2 Comparison of recognition rate in ORL dataset |
针对人脸识别的图片预滤波处理阶段, 提出了一种基于学习的核微分滤波器。该滤波器的设计目标是增加滤波后图像的类内相似度同时减小类间相似度, 从而便于后继的特征提取及识别。通过将滤波器学习转换到高维核空间, 隐含在图像中的非线性信息得以更充分的利用。此外, 在滤波器学习中引入图像的二阶微分信息, 进一步增强了学习滤波器的鉴别能力。在AR库和ORL库上的实验对比结果验证了本文方法的有效性。
| [1] | KIM K. Face recognition using principle component analysis[C]//Proceedings of the 1996 International Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 1996: 586-591. |
| [2] | BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19 (7) : 711-720. doi: 10.1109/34.598228 |
| [3] | CEVIKALP H, NEAMTU M, WILKES M, et al. Discriminative common vectors for face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27 (1) : 4-13. doi: 10.1109/TPAMI.2005.9 |
| [4] | BAUDAT G, ANOUAR F. Generalized discriminant analysis using a kernel approach[J]. Neural Computation, 2000, 12 (10) : 2385-2404. doi: 10.1162/089976600300014980 |
| [5] | CEVIKALP H, NEAMTU M, WILKES M. Discriminative common vector method with kernels[J]. IEEE Transactions on Neural Networks, 2006, 17 (6) : 1550-1565. doi: 10.1109/TNN.2006.881485 |
| [6] | LIU C, WECHSLER H. Gabor feature based classification using the enhanced Fisher linear discriminant model for face recognition[J]. IEEE Transactions on Image Processing, 2002, 11 (4) : 467-476. doi: 10.1109/TIP.2002.999679 |
| [7] | AHONEN T, HADID A, PIETIKAINEN M. Face description with local binary patterns: Application to face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28 (12) : 2037-2041. doi: 10.1109/TPAMI.2006.244 |
| [8] | LIAO S, ZHU X, LEI Z, et al. Learning multi-scale block local binary patterns for face recognition[C]//ICB 2007: Proceedings of the 2007 International Conference on Advances in Biometrics. Berlin: Springer, 2007: 828-837. |
| [9] | ZHANG W, SHAN S, GAO W, et al. Local Gabor Binary Pattern Histogram Sequence (LGBPHS): a novel non-statistical model for face representation and recognition[C]//ICCV 2005: Proceedings of the Tenth IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2005, 1: 786-791. |
| [10] | JABID T, KABIR M H, CHAE O. Facial expression recognition using Local Directional Pattern (LDP)[C]//Proceedings of the 2010 IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2010: 1605-1608. |
| [11] | LEI Z, YI D, LI S. Discriminant image filter learning for face recognition with local binary pattern like representation[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2012: 2512-2517. |
| [12] | LEI Z, PIETIKAINEN M, LI S Z. Learning discriminant face descriptor[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36 (2) : 289-302. doi: 10.1109/TPAMI.2013.112 |
| [13] | SCHOLKOPFT B, MULLERT K R. Fisher discriminant analysis with kernels[EB/OL].[2016-03-01]. http://courses.cs.tamu.edu/rgutier/csce666_f16/mika1999kernelLDA.pdf. |




