2. 教育部数据工程与知识工程重点实验室(中国人民大学), 北京 100872
2. Key Lab of Data Engineering and Knowledge Engineering of Ministry of Education(Renmin University of China), Beijing 100872, China
算法交易,是使用复杂的计算机程序(软件),实现交易过程的自动化。这些程序使用机器学习或者数据挖掘算法,分析大量的数据,进而决定是否进行交易,包括买进还是卖出,什么时候进行交易,以及订单的大小等。
算法交易具有若干优势。包括:1) 交易模型体现出很强的一致性。2) 交易模型可以同时处理多个金融资产(股票、期货等)。3) 交易模型进行数据分析和执行订单的速度,比人更快。其中,最主要的优势是交易模型不像人类投资者那样具有情感,它仅仅依赖于数据分析结果,进行交易决策,于是,它能够保持一致的交易决策和行为。相反,由于人类投资者受到自己情感的影响,在投资过程中,很难坚持既定的原则。
金融市场(股票市场、期货市场等)是一个动态变化的复杂系统[1],进行价格预测是一件很困难的事情。著名的有效市场理论(Efficient Market Hypothesis,EMH)[2]指出,所有可以获得的信息,立即反映在股票价格的变化中,只有新的信息到达,才能引起股票价格的新变化。于是,对金融市场的价格运动进行预测,几乎是不可能的,但是,信息的传播是有一定的延迟的。另外,不同的人对接收到的同一信息,有不同的解释。很多研究表明,一些宏观经济变量(Macroeconomic Variables)和技术指标(Technical Indicators),在一定程度上,能够预测股票价格的未来变化。比如,文献[3]的研究表明,南亚地区的四个股票市场的未来收益,存在一定的可预测性(Predictability)。
在实际应用中,世界范围内的各大银行、对冲基金(Hedge Funds)广泛采用算法交易技术和模型。根据文献[4]的调查,仅仅在美国,在2000年,从华尔街的算法交易系统发起的订单(Order),占到全美股票交易量的40%。到2008年,这个数字攀升到60%,而到了2014年,这个数据超过了70%。
人们采用两种分析策略,来预测股票价格的变化,一种是基本分析(Fundamental Analysis),一种是技术分析(Technical Analysis)[5-6]。所谓基本分析,是通过分析影响股票内在价值的各种经济因素,对股票价格作出预测,一般用于中长期预测。技术分析派,则相信历史总会重演。他们使用作图工具、指标计算和数据分析工具,寻找可能盈利的价格变化模式(Pattern)。技术分析一般用于中短期价格预测。
本文提出一种通过使用若干导出指标训练统一的交易模型的策略,以及投资组合多样化的方法,来提高交易模型的稳健性。所谓交易模型的稳健性,指的是模型的利润率曲线,具有较小的波动性,没有大起大落。该投资组合多样化方法,是为一个基于支持向量回归(Support Vector Regression,SVR)技术的交易模型服务的。本研究为该模型构造了基于一些常用指标的导出指标,这些指标较好地刻画了价格的变化模式、超买/超卖市场状态以及背离市场状态等。本研究首先对这些指标进行规范化处理,然后用于训练一个通用模型。训练后的交易模型可以用于不同的股票价格的预测。在此基础上,为了实现投资组合的多样化,本研究把股票聚类到不同的类别中。股票的相似性,定义为交易模型在这些股票上的利润率曲线之间的相似性。这样定义相似性,其目的是,当交易模型预测发生错误的时候,系统将进行止损,如果直接在价格数据上定义相似性,不能反映实际交易中的止损操作,是不可靠的。
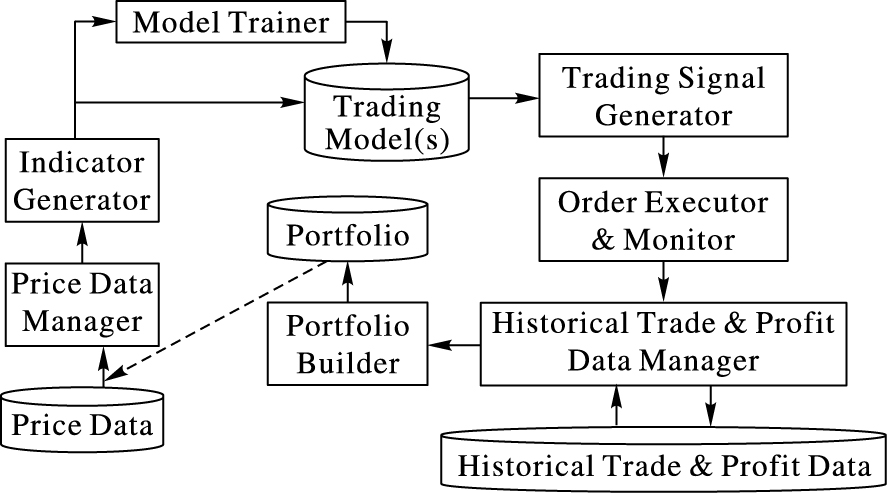
1 基于支持向量回归的算法交易模型 1.1 交易系统架构本文首先介绍整个交易系统的架构,然后介绍交易模型细节。整个交易系统的各个组件及其关系,如图 1所示。本文通过交易模型的创建、交易模型的训练以及交易模型的运行来介绍这些组件及其功能。
|
图 1 交易系统的各个组件 Figure 1 Various components of the trading system |
首先,本研究创建了一个基于SVR技术的交易模型。该模型不仅使用了一些常用的技术指标作为输入,还基于这些指标,构造了一些导出指标,以刻画价格的变化模式、超买/超卖市场状态、以及背离市场状态。
接着,本研究使用股票价格数据对交易模型进行训练。这些价格数据从Yahoo Finance网站上下载,并且保存到本地备用。Price Data Manager从本地硬盘提取价格数据,馈入Indicator Generator,计算各种技术指标。计算出来的指标,交给Trainer,以便对模型进行训练。本研究从Yahoo Finance下载了900只股票、10年的价格数据。其中9年的数据用于训练(Training),最后1年的价格数据用于验证(Testing)。本研究使用遗传算法对交易模型的参数进行了优化。
为了泛化交易模型(适用于不同的股票),本研究在滑动的时间窗口(Moving Window)内,对指标进行了规范化处理。价格的变化规律不仅在一只股票价格的历史演变中重现,而且在不同股票价格的历史演变中重现。
本研究使用验证数据,对训练好的交易模型进行验证。在验证阶段,从验证数据计算指标,输入到训练好的交易模型,进行价格预测,根据预测结果,决定是否交易。基于模型的预测,Trading Signal Generator产生买/卖交易信号(BUY/SELL Signals),交给 Order Executor & Monitor 执行。
Order Executor & Monitor 对投资组合中的每只股票的每个交易进行监控,记录盈利和损失情况。Historical Data Manager 负责管理交易数据(Trade)和利润数据(Profit)。
本研究将考察三种为交易模型建立投资组合的方法。1) 第一种方法,从市场上随机选择Np只股票,给这些股票平均分配总资金的1/Np。这里Np是投资组合的股票数量。2) 第二种方法,使用交易模型,预测每只股票的未来收益(在1.2.4 节详述预测过程),然后根据预期收益对股票进行排序,选择Np只股票构成投资组合。3) 第三种方法,首先根据交易模型在股票上最近30天的交易利润曲线(有些股票并未真正发生交易,可以使用模拟办法计算这个利润曲线),计算股票间的相似性,进而把股票聚类到不同类别。在每个类别内,对各个股票根据预期收益率进行排序。从每个类别中,选择若干只股票,总数是Np只股票,构成多样化的投资组合。这个方法将在第2章进行详细介绍。系统记录的交易历史数据和利润数据(Historical Trade and Profit Data),将用来计算股票之间的相似度。
本文提出的投资模型多样化方法,和交易模型配合,为其建立投资组合。当一个投资组合建立以后,资金被平均分配到各只股票。如果交易模型预测到一定的利润,系统将为某只股票建立头寸(买入),并且持有。随着时间的推移,如果交易模型的预测不准,价格掉头向下,超过预先设置的阈值,将引发止损操作。否则,股票一直持有到卖出日(SELL day),然后售出。几天以后,当所有的股票都卖出,系统将基于新的数据,建立新的投资组合,开始新一轮交易过程。
1.2 创建交易模型 1.2.1 SVM和SVR支持向量机(Support Vector Machine,SVM)技术最先由Vapnik等于1990年提出来。该技术分为两类,包括支持向量分类(Support Vector Classification,SVC,一般仍称为SVM),以及支持向量回归(Support Vector Regression,SVR)。
SVM的目的,是找到高维空间的一个超平面(Hyper Plane),把正例数据点(Data Points,也叫向量)和负例数据点很好地分开,而且使得支持向量到超平面的距离最大。如果低维空间里的数据点,不能用一个超平面分开,可以使用一个核函数(Kernel Function),把这些数据点变换为高维空间的向量,以便把它们在高维空间中较为容易地分开。常用的核函数,包括多项式核函数(Polynomial)以及径向基函数(Radial Basis)。一般用一个正则化参数(Regularization Parameter)C,调节距离最大化和分类误差最小化之间的平衡。
SVR技术则训练出一个模型,它可以接受新的输入,预测一个目标值。这个模型在训练的时候,针对训练数据,在高维空间中拟合出一个超曲线(Hyper Curve),把尽量多的训练数据点,包含到包围这个曲线的一个管道(Enveloping Tube)中。具体来讲,假设,现有xi∈Rd(i=1,2,…,N),构成d维空间的输入向量。每个xi对应一个yi∈R。给定一个任意的ε>0,如果存在一个超曲线f(x)=〈w,x〉+b,w∈Rn,b∈R,对于∀(xi,yi)∈S,符合|yi-f(xi)|≤ε,那么f(x)=〈w,x〉+b称为训练样本的ε-线性回归。ε-线性回归问题,可以转化为一个优化问题,形式如下:
最小化
约束条件为|(wT·xi)+b-yi|≤ε(i=1,2,…,n),这个优化问题可以转化为一个对偶问题,并且用二次规划(Quadratic Programming)方法加以解决。本研究在标准SVR技术上实现了交易模型,并使用了径向基核函数:K(xi,yi)=exp(-γ‖xi-yi‖2)。
1.2.2 指标计算以及规范化处理用某只股票的价格对交易模型进行训练,很难泛化到其他股票。本研究对指标进行了规范化,忽略了价格数据的绝对值,刻画了价格的近期的相对变化趋势。
本文认为,不仅各只股票的价格变化,不断重演其历史。某些价格变化模式,也能够在不同股票的价格演变中观察得到,也就是历史在不同的股票间重演。于是本研究用若干只股票的价格上计算的规范化指标,训练了一个统一的模型,并且把这个模型应用到所有的股票上。
本研究从价格数据上计算若干指标,用于对交易模型进行训练,指标(Indicators)也称为特征(Features)。
1) 简单移动平均指标。
简单移动平均(Simple Moving Average)指标的计算公式为SMA=(Ct+Ct-1+Ct-2+…+Ct-n+1)/N,其中Ct 表示第t天的收盘(Close)价,Ct-1 表示第t天的前一天的收盘价等。
简单移动平均指标,对移动窗口内的价格计算均值,对价格数据的变化进行了平滑。本研究的交易模型,主要用于短期预测,所以使用了两个移动平均指标,分别是5天的移动平均(称为短期移动平均(Short SMA,SSMA)),和10天的移动平均(称为长期移动平均(Long SMA,LSMA))。
对于移动平均指标的使用,有一个通用的投资策略,称为长期和短期移动平均指标的交叉(Crossover)策略(http://www.investopedia.com,http://www.stockcharts.com)。这个策略使用短期、长期两个移动平均指标,在趋势性市场行情中,产生买/卖交易信号(BUY/SELL Signals)。如果短期移动平均指标从下往上和长期移动平均指标交叉,并且向上发展,那么价格的总体趋势是向上的,可以产生一个买信号(BUY)。相反,如果短期移动平均指标从上往下和长期移动平均指标交叉,并且向下发展,那么价格的总体趋势是向下的,可以产生一个卖出信号(SELL)。否则,持有资金或者持有股票头寸,不产生任何交易信号。
除了当天的短期和长期移动平均指标(记为SSMA0,LSMA0)以外,为了刻画最近一段时间内短期移动平均指标和长期移动平均指标之间的相对运动趋势,比如两者是不断靠近还是不断远离等,本文构造了另外一个导出指标,称为CSMA(Crossover Indicator for SMA)。CSMA指标有10个元素,即CSMA=〈CSMA0,CSMA-1,CSMA-2,…,CSMA-9〉,其中CSMA0=SSMA0-LSMA0,CSMA-1=SSMA-1-LSMA-1,CSMA-2=SSMA-2-LSMA-2等。这里0表示当天,-1表示昨天,-2表示前天等,一直到-9表示9天之前的那天。
本研究将为所有股票建立一个统一的交易模型,而不是为每只股票单独创建一个交易模型。SSMA0,LSMA0以及CSMA在用于模型训练之前,需要进行规范化处理。SSMA0,LSMA0根据计算这两个指标的价格数据的最大值和最小值,进行规范化;而CSMA则基于CSMA00,CSMA0-1,CSMA0-2,…,CSMA0-9等10个元素的最大值和最小值进行规范化。
短期和长期移动平均指标的交叉,是一个落后的指标(Lagging Indicators),当交叉发生的时候,价格已经开始攀升或者下跌。所以,本研究需要其他指标来补充,以便交易模型能够更为准确地预测价格变化。
2) 相对强弱指标。
相对强弱指标(Relative Strength Index,RSI)通常用来确定超买和超卖的市场状况,RSI指标在0~100变动。当RSI指标大于70的时候,表明某只股票已经处于超买状态,近期价格有可能下跌。当RSI指标小于30,则表明某只股票处于超卖状态,近期价格有可能上升。
RSI指标的计算公式为:
| $RSI=100-\frac{100}{T};T=1+\frac{\left( \sum\limits_{i=0}^{n-1}{U{{P}_{t-i}}} \right)/n}{\left( \sum\limits_{i=0}^{n-1}{D{{W}_{t-i}}} \right)/n}$ |
其中:UPt表示第t天的价格上涨变化量,而DWt表示第t天的价格下跌变化量。
本研究把当天的RSI指标作为一个训练模型用的特征(称为RSI0)。本研究还对如下重要时刻感兴趣:①RSI曲线(由最近几天的RSI指标组成)从下往上突破70阈值;②RSI曲线从上往下突破70阈值;③RSI曲线从下往上突破30阈值;④RSI曲线从上往下突破30阈值;⑤RSI指标在(30,70) 震荡。
本文使用一个CRSI(Crossover Indicator for RSI)指标来刻画上述重要时刻。这个指标包含10个元素,CRSI0,CRSI-1,CRSI-2,…,CRSI-9,对应今天、昨天、前天等。CRSI0的计算规则是,如果今天的RSI指标超过70,CRSI0置为1,如果今天的RSI指标低于30,CRSI0置为-1,否则CRSI0置为0。其他元素,按照同样规则进行计算,只不过参考的是昨天、前天…的RSI指标。把这些状态组合在一个向量中,记录了RSI指标的近期演化的趋势。
此外,本研究基于RSI指标,构造另外一个动量指标MUMRSI(Momentum for RSI)。这个指标包含9个元素,MUMRSI0,MUMRSI-1,…,MUMRSI-8。MUMRSI0的计算规则为,MUMRSI0=RSI0-RSI-1。其他元素按照类似的方法进行计算。这个指标,记录了最近9天内,每天的RSI指标,相对于前一天是如何变化的。
3) Larry William’s R%指标。
Larry William’s R%指标(简称W%R),是一个随机摇摆(Stochastic Oscillator)指标。W%R的计算公式为W%R=
类似于对RSI指标的处理,本研究使用当天的W%R(W%R0,0表示当天,-1表示前一天)作为训练模型的一个特征。本文还对如下重要时刻感兴趣:①W%R曲线(由最近几天的W%R指标组成)从下往上突破-80阈值;②RSI曲线从上往下突破-80阈值;③RSI曲线从下往上突破-20阈值;④RSI曲线从上往下突破-20阈值;⑤RSI指标在(-80,-20) 震荡。
本研究使用一个CW%R(Crossover Indicator for W%R)指标来刻画上述重要时刻。这个指标包含10个元素,CW%R0,CW%R-1,CW%R-2,…,CW%R-9,对应今天、昨天、前天等。CW%R0的计算规则是,如果今天的W%R指标超过-20,CW%R0置为1,如果今天的RSI指标低于-80,CW%R0置为-1,否则CW%R0置为0。其他元素,按照同样规则进行计算,只不过参考的是昨天、前天…的W%R指标。把这些状态组合在一个向量中,记录了W%R指标的近期演化的趋势。
此外,本研究基于W%R指标,构造另外一个动量指标MUMW%R(Momentum for W%R)。这个指标包含9个元素,MUMW%R0,MUMW%R-1,…,MUMW%R-8。MUMW%R0的计算规则为,MUMW%R0=W%R0-W%R-1。其他元素按照类似的方法进行计算。
4) MACD指标及导出动量指标。
在股票价格的技术分析中,MACD指标(Moving Average Convergence Divergence)经常被用到。MACD 线通过把每天的12天的EMA(Exponential Moving Average)减去26天的EMA,绘制出来。然后,MACD的 9天的EMA线用作一个信号线(Signal Line),用来确定价格是否发生反转(Reversal)。
投资者一般寻找如下的投资机会,包括以下内容。①信号线交叉(Signal Line Crossovers):当MACD指标从下往上和信号线交叉,这是一个牛市信号线交叉;当MACD指标从上往下和信号线交叉,这是一个熊市信号线交叉。②中线交叉(Centerline Crossovers):当MACD从下往上越过x轴,也就是12天的EMA线从下往上越过26天的EMA线,这是一个牛市中线交叉;当MACD从上往下越过x轴,也就是12天的EMA线从上往下越过26天的EMA线,这是一个熊市中线交叉。③价格变化和MACD指标变化趋势的背离(Divergences):当股票价格连创新低,但是MACD却创出新高,表明一个牛市背离(Bullish Divergence)正在形成。股票价格连创新低,表明当前的价格基本走势是下跌趋势(Downtrend),并且还将持续,但是MACD连创新高,表明下跌的动量(Downward Momentum)正在减弱。牛市背离,一般预示着趋势正在反转(Trend Reversal),股票价格随后将有较大的回升。
Google公司的股价,在2008年10月到12月间,股票价格连创新低,而MACD连创新高,形成了一个牛市背离(Bullish Divergence)。于是紧接着,股票价格有一定的上涨(http://stock.finance.sina.com.cn/usstock/quotes/GOOG.html)。
相似地,当股票价格连创新高,但是MACD连创新低,意味着一个熊市背离(Bearish Divergence)正在形成。股票价格连创新高,意味着股票价格处在上升趋势中。熊市背离,一般也预示着趋势正在反转(Trend Reversal),股票价格随后将有较大的下跌。
为了刻画以上描述的信号线交叉,本文计算了一个SCMACD(Signal Line Crossover MACD)指标。这个指标将描述如下重要的时刻:①MACD从下往上和信号线交叉。②MACD从上往下和信号线交叉。③MACD在信号线之上、或者之下演化,没有与其交叉。SCMACD指标是一个向量,包含10个元素,即SCMACD0,SCMACD-1,…,SCMACD-9。SCMACD0元素按照如下规则计算,如果该天的MACD指标在信号线之上,那么SCMACD0置为1,如果该天的MACD指标在信号线之下,那么SCMACD0置为-1,其他元素按照同样规则进行计算,只不过参考的是昨天、前天…的MACD指标等。
类似地,为了刻画中线交叉,本研究计算了CCMACD(Centerline Crossover MACD)指标。这个指标将描述如下重要的时刻:①MACD从下往上和中线(Centerline)交叉。②MACD从上往下和中线交叉。③MACD在中线之上、或者之下演化,没有与其交叉。CCMACD指标是一个向量,包含10个元素,即CCMACD0,CCMACD-1,…,CCMACD-9。CCMACD0元素按照如下规则计算,如果该天的MACD指标在中线之上,那么CCMACD0置为1,如果该天的MACD指标在中线之下,那么CCMACD0置为-1,其他元素按照同样规则进行计算,只不过参考的是昨天、前天…的MACD指标等。
本研究使用两个指标来刻画牛市背离和熊市背离。从MACD指标导出的动量指标MUMMACD,其计算公式为MUMMACD=MUM0-MUM -9 ,其中:MACD0 为当天的MACD指标,而 MACD-9 当天之前第9天的MACD指标。股票价格的动量指标(Momentum of Price)MUMc,使用类似的方法来计算,其计算公式为MUMc = C0 - C-9 。其中C0为当天的股票收盘价,而C-9为当天之前第9天的股票收盘价。在计算这两个指标之前,MACD指标和股票价格事先经过规范化处理。表 1总结了交易模型使用的13个指标。
| 表 1 指标及其描述 Table 1 Index and description |
为了进行交易模型训练,从训练样本的开始时间戳,开始计算表 1所示的各个指标。对于5天的SMA,可以在第5天获得第一个有效的SMA(5) ,因为该指标是对前五天(包括当天)的收盘价的均值。对于10天SMA来讲,需要等到第10天,才能获得第一个有效的SMA(10) 。用于计算上述指标的最长的时间区间是26天(计算MACD指标),于是从第26天开始,就获得有效的指标集,包含13个指标。从此以后的每天,都可以计算出对应当天的有效的13个指标。
对于获得有效的13个指标的每一天,利用一天以后的股票价格,计算一个利润率,表示如果当天购买股票,隔天卖出,能够创造什么样的利润率。利润率的计算公式为Rprofitt+1=(Ct+1-Ct)/Ct。13个指标、以及天数(1天)作为输入,利润率Rprofitt+1作为输出,形成一个训练样本。除此之外,针对2天、3天、4天、5天、6天、以及7天构造训练样本。这些训练样本将用于交易模型的训练。表 2展示了针对每天指标及其后第1到第7天的预期利润率,所构造的训练样本。
| 表 2 每天的7个训练样本 Table 2 7 training samples per day |
在支持向量回归(SVR)模型中,有两个可调参数,一个是正则化参数C,一个是径向基核函数的γ参数。本文使用遗传算法,对这两个参数进行优化。
1.2.4 使用交易模型进行预测交易模型经过训练以后,它能够根据输入的指标,预测股票的短期价格变化,指导交易。每一轮交易包含4个步骤,分别是:1) 建立投资组合;2) 产生交易信号;3) 买入并且持有股票,直到预期的卖出日,或者止损;4) 清空当前股票头寸(Position),重新回到步骤1) ,开始下一轮交易。
这四个步骤详述如下:
1) 投资组合管理(Portfolio Management)。一轮投资的发起,从建立投资组合开始。使用的方法在1.1节中已经简单介绍,其中的投资组合多样化方法,将在第2章详细介绍。
2) 利用交易模型进行预测,并且产生交易信号。本研究把交易模型应用到测试数据上,进行短期预测(Short Term Price Prediction)和交易。从测试样本的开始时间戳之后的第26天开始,每天都能够计算出有效的13个指标。这些指标,加上天数(1~7) ,被输入系统,预测1天~7天以后的预期利润(Expected Profit Ratio)。
这7个预测作为候选集,本研究将基于这个候选集,产生买入交易信号(BUY signal)。决策的原则是,对7个预测的预期利润率进行排序,选出最高的预期利润,并且检查:①该利润率是否超过一定的阈值,以便覆盖交易成本。②没有一个更早(天数更少)的预期价格变化,可能引起一个止损操作。倘若如此,就产生一个买入交易信号;否则,继续寻找第二个最好的预期利润率。如果没有一个预期利润率符合上述条件,本轮不对该股票进行交易。
下面给出一个具体例子,表 3中的第一部分列出了交易模型对股票A的若干预测,第二部分列出了交易模型对股票B的若干预测,而第三部分则列出了交易模型对股票C的若干预测(表中的百分比为交易模型预测的针对各个天数的利润率)。本研究采用的止损阈值为下跌5%,可以买入的上涨阈值为7%。
| 表 3 预期利润与交易信号的产生 Table 3 Expected profits and the generation of trading signals |
其中,从表 3的第一部分,可以看到针对7天的预测获得最高的预期利润,并且没有一个更早的预期价格变化会引起止损操作。于是交易模型产生一个买入交易信号,买入该股票,并且持有7天以后卖出。
从表 3的第二部分可以看出,针对7天的预测,获得最高的预期利润,但是,4天的预测显示价格将有5.5%的下跌,这个下跌幅度超过了止损阈值。于是,选择3天的预测,产生一个买入交易信号,因为它不仅超过可以买入的阈值,并且它之前没有一个预测的价格变化,会引起一个止损操作。
而对于股票C(表中的第三部分),从这些天的预测中,没有看到任何的交易机会,于是不产生任何交易信号。
交易模型产生一个买入信号以后,根据分配给这只股票的资金,买入该只股票。
3) 持有股票到预期的卖出日或者进行止损。交易模型监控每只购入的股票的价格变化,如果价格没有按照预期上涨,而是下跌到止损阈值以下,那么对该只股票进行止损,即及时卖出,减少损失。
如果没有发生止损情况,股票将持有到预期的卖出日期(SELL day,参考表 3中的预测时使用的天数),并且卖出股票。比如对于表 3中的股票A,买入该股票,并且持有7天,到第7天卖出。
4) 下一轮交易。当所有的股票已经卖出,进入下一轮交易过程,也就是回到步骤1) 。
2 投资组合的多样化投资组合的多样化,就是遵循“鸡蛋不要放在一个篮子里”原则进行投资,其目的是减少大的损失。当投资组合里某些股票的价格变化具有很强的相关性的时候,如果交易模型预测不准确,对这些股票同时止损,将引起较大的损失。
本研究使用聚类技术,把所有可交易的股票划分到不同类别中,然后从各个类别选择部分股票,构成多样化的投资组合。股票之间的相似性,定义为近期交易模型在这些股票上的交易性能,也就是交易模型在这些股票上的利润率曲线之间的相似性。
2.1 股票之间的相似性定义(交易模型在股票上的收益)本研究没有在股票价格上,直接计算股票之间的相似性。而是在股票价格上,运行交易模型,并且记录交易模型产生的交易信号和交易利润率,进而计算股票间的相似性。在最近的一段时间内,交易模型历次交易对应的交易利润率,形成一个利润率曲线,对应一个利润率向量(Profit Vector,PV)。股票之间的相似性,定义为其PV的相似性。
对于不同的股票,交易模型在一定时间段内,产生的交易次数不一样。也就是,两只股票的PV拥有不同的元素,隶属不同的高维向量空间,比如PV1∈Rn,而PV2∈Rm,m≠n。本文使用DTW(Dynamic Time Warping)技术,对两只股票的PV进行相似性计算。该方法能够计算时间序列数据的相似性,即便两者的数据点数不一样。
本研究把投资组合内的每只股票近30天的买卖交易记录下来,基于这些交易计算利润率,然后根据利润率计算每对股票之间的相似性。不在投资组合里的其它股票,并未进行实际交易,而是通过模拟交易(Simulation Trading)记录这些股票上的交易信息以及利润率,这些模拟交易的利润率反映了交易模型在这些股票上的性能表现,基于此计算这些股票之间的相似度。
2.2 股票聚类聚类技术把相似度大的股票聚集在一个类别中,把相似性小的股票分解到不同的类别中。可以用于聚类的方法有两种:1) 第一种方法,把股票的相似系数,组织成一个N*N矩阵S,N是股票的个数,Si,j 是股票i和股票j之间的相似性。然后在系数矩阵上,使用传统的聚类方法,把股票划分到不同类别。2) 第二种方法,基于股票之间的相似性,建立一个股票之间的社交网络,形成一个无向带权重的图(Undirected Weighted Graph)。每个节点表示一只股票,每条边(带权重)表示股票之间的相似性。建立好股票的社交网络后,可以使用网络社区挖掘方法(Community Detection) [7-8],把股票划分到不同的类别,每个类别对应一个社区。其中,文献[8]提供了一种针对带权重的社交网络的社区挖掘方法。
本研究使用第一种方法对股票进行聚类。在未来工作中,将尝试第二种方法,并且与第一种方法进行比较
2.3 根据预期收益率从各个聚类的类别中选择股票完成聚类分析以后,每只股票被划分到不同的类别。从这些类别中,选择一些股票,构成投资组合,投资组合中的股票数量为Np。股票的选择标准是预期收益率,预期收益率的计算方法和1.2.4 节描述的方法一致,这里不再赘述。
从每个类别选择的股票数量用公式Ngi=Np*
本研究从Yahoo Finance网站上,获取了上海股票交易所的900只股票的价格信息,时间跨度从2005年到2015年。2005年到2014年的价格数据用于训练,2015年的价格数据用于验证。
对于交易模型的评价,人们最感兴趣的是其年化利润率(Annualized Profit Ratio,也称收益率)。如果一个交易模型,不能在无风险的定期存款以外创造额外的收益,它是没有用的。倘若如此,还不如直接把款项存为定期存款。
本研究的工作,其目的是提高交易模型的稳健性。本研究还使用另外两个性能指标,即最大回撤(Max Drawdown)和夏普指数(Sharp Ratio),来评价本文提出的方法的有效性。
最大回撤指标可以评价一个交易模型选择的投资组合的风险度。最大回撤的计算公式为MDD =(A-B)/A,其中A为最大下跌之前的资产最大净值(Peak Asset Value before Largest Drop),B为 资产净值创出新高之前的最低的资产净值(Lowest Asset Value before New High Established)。比如,一个投资组合的开始净值为$10 000,这个净值经过一系列股票交易以后发生变化,第一天为$17 000,第二天为$8 000,第三天为$13 000,第四天为$7 000,第五天为$19 000,那么,最大回撤为(17 000-7 000) /17 000=52.9%。最高净值$19 000没有用来计算最大回撤,因为这里的回撤是从最高点$17 000开始的。投资模型的最大回撤越小越好。
夏普指数是由William F. Sharpe发明的一个指标。他用标准差(Standard Deviation)以及超额收益(Excess Return),来计算每单位风险获得的收益,这里的风险指的是波动性。假设,投资组合的年化收益率为12%,波动性为10%,无风险的定期存款利率为5%,那么夏普指数为(0.12-0.05) /0.1=70%。投资模型的夏普指数越高,显示投资模型越稳健,收益越好。
本研究把数据集划分为3个子集,每个子集包含300只股票。本研究在3个数据子集上独立进行实验,并且计算交易模型的年化收益率、最大回撤,以及夏普指数。交易模型使用的初始资金为$1 000 000,投资组合的容量为25只股票,无风险的定期存款利率为3.6%。
3.2 通用交易模型和特定模型的性能比较本研究进行的第一个实验,用于比较为所有股票建立的通用模型,与为每只股票建立的特定模型的性能。
首先,为所有的股票训练了一个通用模型,然后为这个模型建立多样化的投资组合进行交易;接着,为每只股票创建特定的交易模型(仅适用于该股票);然后,建立多样化的投资组合,针对每只股票,使用特定交易模型进行交易。表 4显示了实验的最终结果。
| 表 4 通用交易模型和特定交易模型的性能比较 Table 4 Performance comparison of general trading model and specific trading model |
对于数据子集1,特定模型获得了11.91%的年化收益率,比通用模型的年化收益率7.95%要高,但是在另外两个指标上,即最大回撤和夏普指数,通用模型表现比特定模型要好。通用交易模型的最大回撤为5.34%,比特定模型的13.32%小。通用模型的夏普指数为88.78%,高于特定模型的81.30%。
这些结果显示,虽然通用模型的年化收益率较小,但是它更加稳健。在数据子集2和数据子集3上,通用模型和特定模型在三个指标上显示出类似的差异。为了检验结论的可靠性,本文进行了T检验,比较通用模型和特定模型的最大回撤的均值。检验结果显示两者存在统计学意义上的显著差异(t=-24.988,and p=0.001 6<0.05) 。另外一个T检验,也验证了两者在夏普指数上的显著差异。
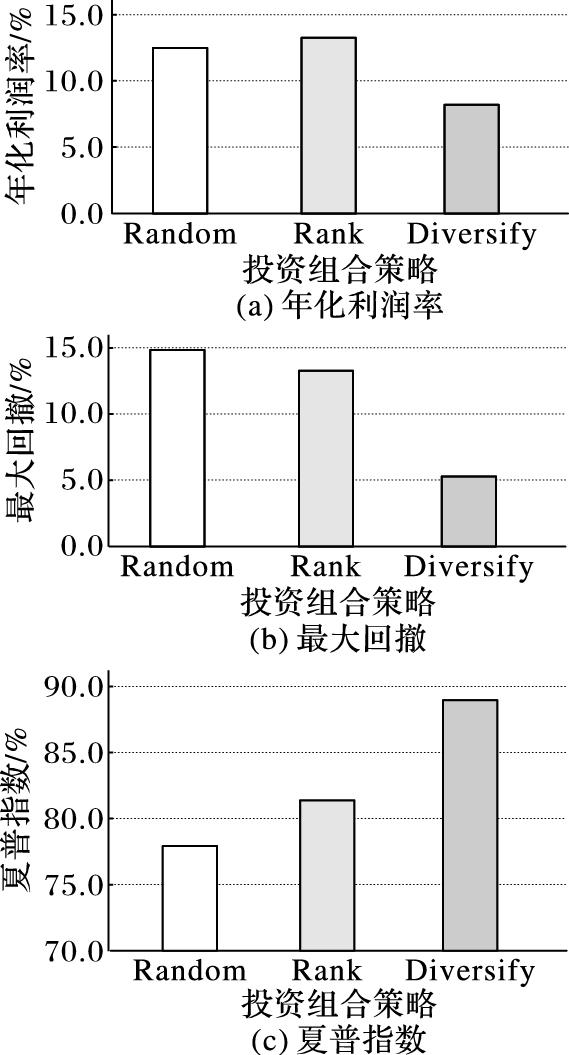
3.3 不同投资组合构造方法的比较第二个实验的目的,是比较不同的投资组合构造方法的性能。投资组合的构造方法为:1) 随机选择法(Random);2) 排序法(Rank);3) 多样化方法(Diversifying)。本文用通用的交易模型进行实验,从900只股票里建立包含75只股票的投资组合。实验结果如表 5和图 2所示。
| 表 5 三种投资组合构造方法的比较 Table 5 Comparison of three methods of portfolio construction |
|
图 2 三种投资组合构造方法的比较 Figure 2 Comparison of three methods of portfolio construction |
可以看出,多样化的投资组合(Diversifying)获得了8.06%的年化收益率,比另外两种方法要低(Random和Rank),但是Diversifying方法在最大回撤和夏普指数两个指标上,都超过了Rank和Random。这个结果显示,多样化的投资组合提高了交易模型的稳健性。
出乎意料的是,Random方法的年化利润率高达11.82%,这可以归因于支持向量回归具有较强的非线性预测能力。
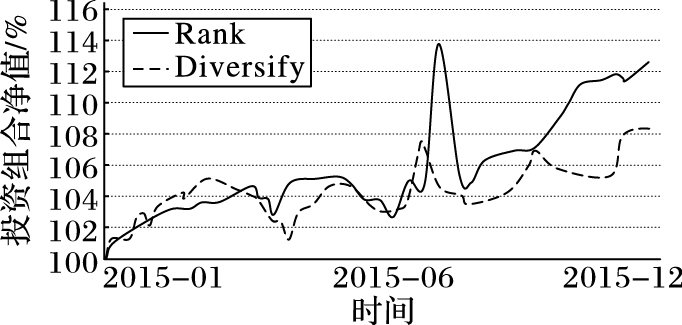
图 3展示了Rank和Diversifying两个投资组合的净值变化情况(2015年)。x轴表示时间从2015年1月到2015年12月,y轴表示投资组合的净值的变化,用相对于资产净值的初值的百分比表示。可以直观地观察到,多样化的投资组合,其净值曲线的波动性较小。由于Random投资组合的演化趋势和Rank投资组合类似,所以没有一同绘制在图 3中。
|
图 3 两个投资组合净值的变化情况 Figure 3 Changes in net value of two investment portfolios |
人们使用各种机器学习和数据挖掘方法,来进行股票价格的预测[6],具体的技术包括支持向量机和支持向量回归(SVM and SVR) [6, 9]、人工神经网络[10]、朴素贝叶斯技术[11]、模糊系统[12]、遗传算法[13]等。
支持向量回归技术,以其强大的非线性建模能力,已经在股票价格预测领域得到了广泛的应用[6]。人们还尝试了把该技术和其他技术结合,包括小波分析(Wavelet Analysis)、粒子群优化(Particle Swarm Optimization)、神经网络(Neural Network)等。有些基于SVR的交易模型,不仅使用技术指标(Technical Indicators)作为输入,同时把文本分析的结果也作为新的特征加以运用。本文也基于SVR技术建立了交易模型,本文工作的主要区别是,在常用的基础指标上,本文手工构造了一些导出指标,这些指标刻画了典型的价格运动模式、市场里的超买/超卖状况和背离状况。此外,本文对指标进行了规范化处理,以便训练出一个适用不同股票的通用交易模型。
文献[14]把关联规则分析和聚类分析结合起来,研究不同金融市场的联动性(Co-movement),并且建立一个模型,用于投资组合推荐。文献[15]提出了一种投资组合的多样化方案。该方案通过K-means聚类算法和社交网络的社区发现(Community Detection)算法实现。其使用的相似性系数,依据一对股票在一段时间内的预期收益来计算。即便两只股票的价格变化表现出一定的相似性,但是当把止损操作考虑进来以后,交易模型在两者上的盈利表现不一定一致。于是,本研究采用了和上述文献不同的相似度计算方法,它通过交易模型在两只股票上的近期历史表现(即收益情况)来计算股票相似度,把交易模型预测不准确的情况考虑进来。如果预测不准确,并且价格下跌到一定程度,交易系统将激发止损操作。传统相似度计算方法,没有考虑到这种情况,把一些股票分配到同一个聚类,在预测不准确的时候,引起雪崩式的止损操作,导致比较大的损失。
4.2 讨论本文通过一些手工构造的导出指标,刻画了典型的价格运动模式、超买/超卖市场状态以及背离市场状态。近年来,深度学习技术展现出优异的性能,它能够无监督地从数据中学习各个抽象级别(从低级到高级的)的特征。使用深度学习技术[16-17]识别股票价格图中的模式,是一个值得研究的课题。
5 结语本研究基于支持向量回归技术创建了一个交易模型。对于模型的输入向量(特征),基于常用指标构造了若干导出指标,以便刻画典型的价格变化模式、超买/超买市场状况以及背离市场状况。这些指标经过规范化处理,为所有股票训练一个统一的交易模型。为了提高该交易模型的稳健性,提出了投资组合的多样化方法。利用近30天交易模型在不同股票上的盈利表现,计算股票的相似性,并且基于该相似性进行股票聚类,从各个类别中选择部分股票,构成多样化的投资组合。实验结果显示,该交易模型能够对不同股票进行交易,并且创造了超过定期存款利息的收益,显示了其泛化能力。此外,交易模型的利润率曲线的波动性降低了,意味着交易模型的稳健性获得了提高。
| [1] | ABU-MOSTAFA Y S, ATIYA A F. Introduction to financial forecasting[J]. Applied Intelligence, 1996, 6 (3) : 205-213. doi: 10.1007/BF00126626 |
| [2] | FAMA E F. The behavior of stock market prices[J]. Journal of Business, 1965, 38 (1) : 34-105. doi: 10.1086/jb.1965.38.issue-1 |
| [3] | NISAR S, HANIF M. Testing weak form of efficient market hypothesis:empirical evidence from south-Asia[J]. World Applied Sciences Journal, 2011, 17 (4) : 414-427. |
| [4] | STEINER C. Automate This:How Algorithms Came to Rule Our World[M]. London: Portfolio Publishing, 2012 : 75 -99. |
| [5] | MURPHY J J. Technical analysis of the financial markets:a comprehensive guide to trading methods and applications[M]. Upper Saddle River, NJ: Prentice Hall Press, 1999 : 100 -137. |
| [6] | CAVALCANTE R C, BRASILEIRO R C, SOUZA V L F, et al. Computational intelligence and financial markets:a survey and future directions[J]. Expert Systems with Applications, 2016, 55 : 194-211. doi: 10.1016/j.eswa.2016.02.006 |
| [7] | NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E:Statistical Nonlinear and Soft Matter Physics, 2004, 69 (6) : 066133. doi: 10.1103/PhysRevE.69.066133 |
| [8] | CUI A, CHEN D, FU Y. Community detection based on weighted networks[C]//NPC'08:Proceedings of the 2008 IFIP International Conference on Network and Parallel Computing. Washington, DC:IEEE Computer Society, 2008:273-280. |
| [9] | LU C J, LEE T S, CHIU C C. Financial time series forecasting using independent component analysis and support vector regression[J]. Decision Support Systems, 2009, 47 (2) : 115-125. doi: 10.1016/j.dss.2009.02.001 |
| [10] | LI Y H, MA W. Applications of artificial neural networks in financial economics:a survey[C]//ISCID'10:Proceedings of the 2010 International Symposium on Computational Intelligence and Design. Washington, DC:IEEE Computer Society, 2010:211-214. |
| [11] | PATEL J, SHAH S, THAKKAR P, et al. Predicting stock and stock price index movement using trend deterministic data preparation and machine learning techniques[J]. Expert Systems with Applications, 2015, 42 (1) : 259-268. doi: 10.1016/j.eswa.2014.07.040 |
| [12] | CHANG P C, LIU C H. A TSK type fuzzy rule based system for stock price prediction[J]. Expert Systems with Applications, 2008, 34 (1) : 135-144. doi: 10.1016/j.eswa.2006.08.020 |
| [13] | CHEN Y, MABU S, SHIMADA K, et al. A genetic network programming with learning approach for enhanced stock trading model[J]. Expert Systems with Applications, 2009, 36 (10) : 12537-12546. doi: 10.1016/j.eswa.2009.05.054 |
| [14] | LIAO S-H, CHOU S-Y. Data mining investigation of co-movements on the Taiwan and China stock markets for future investment portfolio[J]. Expert Systems with Applications, 2013, 40 (5) : 1542-1554. doi: 10.1016/j.eswa.2012.08.075 |
| [15] | KOOCHAKZADEH N. A heuristic stock portfolio optimization approach based on data mining techniques[D]. Calgary, Alberta, Canada:University of Calgary, 2012:23-69. |
| [16] | TAKEUCHI L, LEE Y. Applying deep learning to enhance momentum trading strategies in stocks[EB/OL].[2016-07-01]. http://cs229.stanford.edu/proj2013/TakeuchiLee-ApplyingDeepLearningToEnhanceMomentumTradingStrategiesInStocks.pdf. |
| [17] | 孙志军, 薛磊, 许阳明, 等. 深度学习研究综述[J]. 计算机应用研究, 2012, 29 (8) : 2806-2810. ( SUN Z J, XUE L, XU Y M, et al. Survey on deep learning research[J]. Application Research of Computers, 2012, 29 (8) : 2806-2810. ) |




