现代计算机集群系统包含大量计算节点,这些节点可以是处于分布式环境下或不同管理域中的独立计算机,例如云计算系统或网格计算系统[1-2],也可以是由Infiniband或三维torus 互联系统连接的单独处理器,例如超级计算系统[3-5]。
假设pi表示节点Ni的计算能力,由n个节点组成的计算系统,其计算能力MP表示为MP=p1+p2+…+pn。节点出现故障会导致计算系统性能降低,即节点Ni出现故障,系统的计算能力将变为MP-pi。若节点具有相同的计算能力p,则系统所能呈现的状态数量共有n+1种情况,计算能力分别为0,p,2p,…,np,其中:0表示所有节点都发生故障,np表示所有节点都正常运行。需要说明的是,本文考虑的集群系统满足:集群的整体性能可以近似为各节点计算能力之和,例如具有前端分发节点的n节点Web集群。当然还存在其他很多分布式计算应用,n个节点之间需要进行进一步的交互以完成计算。对于这些交互应用,“n节点集群计算能力是各节点计算能力之和”这一条件将不满足,该类型集群系统的性能分析研究不属于本文的研究范围。
当节点具有相同计算能力时,将计算能力归一化处理,基于k-to-l-out-of-n结构对系统性能进行建模分析,在 k-to-l-out-of-n结构的n个节点中,需要不少于k个但不多于l个可以正常运行的节点[6-7]。分析系统性能时,所有性能状态可以分成若干种不同情况:L1, L2,…,Lm。例如由n个节点组成的计算系统,如果每个节点的计算能力都为p,采用平均划分的方法,可以把系统性能级别从高到低一共划分若干个级别。例如对于n个节点系统其性能可以简单划分为5个级别,为了进行区分可以分别命名为:极低(0≤P≤np/5-1) ,低(np/5≤P≤2np/5-1) ,中等(2np/5≤P≤3np/5-1) ,高(3np/5≤P≤4np/5-1) ,极高(4np/5≤P≤np)。其中极高性能级别包含n个节点全部正常工作的情况;而极低性能级别包含n个节点全部失效的情况。系统的性能分析可表示为系统处于一个特定性能的概率计算,即计算系统性能P落在某个区间内的概率。上述例子中极低、低、中等、高、极高五种情况分别对应以下结构:0-to-(n/5-1) -out-of-n,n/5-to-(2n/5-1) -out-of-n,2n/5-to-(3n/5-1) -out-of-n,3n/5-to-(4n/5-1) -out-of-n,4n/5-to-n-out-of-n。
当节点数量较大时,采用状态穷举的方法效率较低,此时可以采用含非逻辑的非单调关联故障树分析方法[8]。基于质蕴含的非单调关联故障树分析与基于最小割集的单调关联故障树分析类似,同样存在指数复杂性[9]问题。最近,一些基于二元决策图(Binary Decision Diagram,BDD)[10]的组合方法开始应用于故障树分析[11-14]。与其他方法相比,基于二元决策图的方法显得更加有效,因为BDD可以有效描述布尔函数,并且BDD上的操作可以高效地实现各种布尔运算。但现有的一些基于BDD的方法使用自底向上BDD生成算法,容易产生大量冗余的中间节点,而且这些方法也很难利用k-to-l-out-of-n模型的特殊结构,因此并不能提高模型的生成效率。
本文使用基于BDD的分析方法,对具有k-to-l-out-of-n结构的大型集群系统进行性能分析。在任务执行期间,集群及其节点都是不可修复的。针对节点计算能力相同但故障分布不同的集群,利用k-to-l-out-of-n结构下BDD模型所具有的特殊结构特征,设计了自顶向下BDD生成算法,避免了传统自底向上BDD生成算法中大量中间节点的生成。
1 问题描述形式上,二进制随机变量Xi表示节点Ni的状态,Xi=1表示节点Ni处于非故障状态,Xi=0表示节点Ni处于故障状态;由n个节点组成的计算系统,用X=(X1,X2,…,Xn)表示随机的系统状态向量。因为每个节点Ni有两种状态(故障状态或非故障状态),所以由n个节点组成的计算系统有2n种可能的状态。
x=(x1,x2,…,xn)表示系统状态,xi表示节点Ni的状态。系统在任务时间t内处于状态x的概率计算公式如下:
| $\Pr (\mathit{\boldsymbol{X}}=\mathit{\boldsymbol{x}})=\prod\limits_{i=1}^{n}{({{x}_{i}}\cdot (1-{{F}_{i}}(t))+(1-{{x}_{i}})\cdot {{F}_{i}}(t))}$ | (1) |
Fi(t)表示节点Ni在任务时间t内处于Xi=0(故障状态)时的概率。
系统在任务时间t内处于状态x的计算能力P的计算公式如下:
| $P(\mathit{\boldsymbol{X}}=\mathit{\boldsymbol{x}})=\sum\limits_{i=1}^{n}{{{x}_{i}}\cdot {{p}_{i}}}$ | (2) |
系统在任务时间t内以特定性能L运行的概率,用计算能力P落在区间[LB,UB]内的概率表示,LB表示下限,UB表示上限,计算公式如下:
| ${{\mathit{\Phi }}_{L}}=\Pr (LB\le P\le UB)=\sum\limits_{LB\le P(X=x)\le UB}{\Pr }(\mathit{\boldsymbol{X}}=\mathit{\boldsymbol{x}})$ | (3) |
本文讨论的问题是如何在特定任务时间t内计算ΦL,作以下假设:
1) 计算节点之间相互独立运行,即在整个系统中,一个节点事件(比如节点出现故障)的发生不会影响另一个节点事件的发生;
2) 每个节点处于每个状态的概率可以通过给定参数直接计算获得,即本文只考虑系统级的性能分析,部件级的性能分析不在本文讨论范围内;
3) 系统在使用时不可修复,即节点一旦从非故障状态转换到故障状态,在剩余任务时间内该节点都处于故障状态。
2 实例说明实例系统由6个计算节点组成:N1,N2,…,N6,任务持续时间为100 h。为了说明集群的各个节点具有不同寿命分布,假设节点N1、N2、N3服从参数为λ的指数故障分布,累积分布函数Fi(t)如下:
| ${{F}_{i}}(t)=1-\exp (-{{\lambda }_{i}}t)$ | (4) |
假设节点N4、N5、N6服从参数为λ和β的Weibull故障分布,累积分布函数Fi(t)如下:
| ${{F}_{i}}(t)=1-\exp (-{{({{\lambda }_{i}}t)}^{{{\beta }_{i}}}})$ | (5) |
表 1显示了任务时间为100 h,参数λi和βi分别为给定值时,使用式(4) 或(5) 计算得出的Fi(t)。
| 表 1 节点参数和计算所得的Fi(t) Table 1 Node parameters and calculated Fi(t) |
节点Ni的计算能力为pi,实例系统的最大计算能力MP表示为MP=p1+p2+p3+p4+p5+p6。不失一般性,系统性能P的三种性能分别定义为:低LL(LBL≤P≤UBL),中LM(LBM≤P≤UBM),高LH(LBH≤P≤UBH),LBi(i∈{L,M,H)表示下限,UBi(i∈{L,M,H)表示上限。
当节点相同且计算能力也相同时,将pi归一化处理。表 2显示了对应三种性能的LB和UB值,以及对应的k-to-l-out-of-n模型。
| 表 2 不同性能下的参数设置(pi相同) Table 2 Parameter setting under different performance levels (same pi) |
本文所研究的集群系统性能分析问题可以描述为:在任务时间内,分析集群系统在表 1和表 2的参数设置下,系统处于性能状态LL、LM和LH的概率。需要注意的是,本文关注的是在特定时间内的概率计算,而不是处于稳定状态或长期运行状态的概率计算。
3 基于BDD的性能分析方法本文提出一种基于BDD的性能分析方法对节点计算能力相同的集群系统进行性能分析。该方法由两个步骤组成:1) 使用k-to-l-out-of-n结构生成BDD模型;2) 分析BDD模型并得到系统性能评估指标。
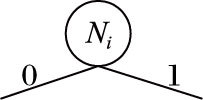
3.1 生成BDD模型每个二状态节点Ni的状态空间存在两种互斥的状态:0表示故障状态,1表示非故障状态。如图 1所示,BDD模型中每个节点Ni都有两条输出边:then-edge用1表示(非故障状态),else-edge用0表示(故障状态)。
|
图 1 与Ni关联的BDD节点 Figure 1 BDD node associated with Ni |
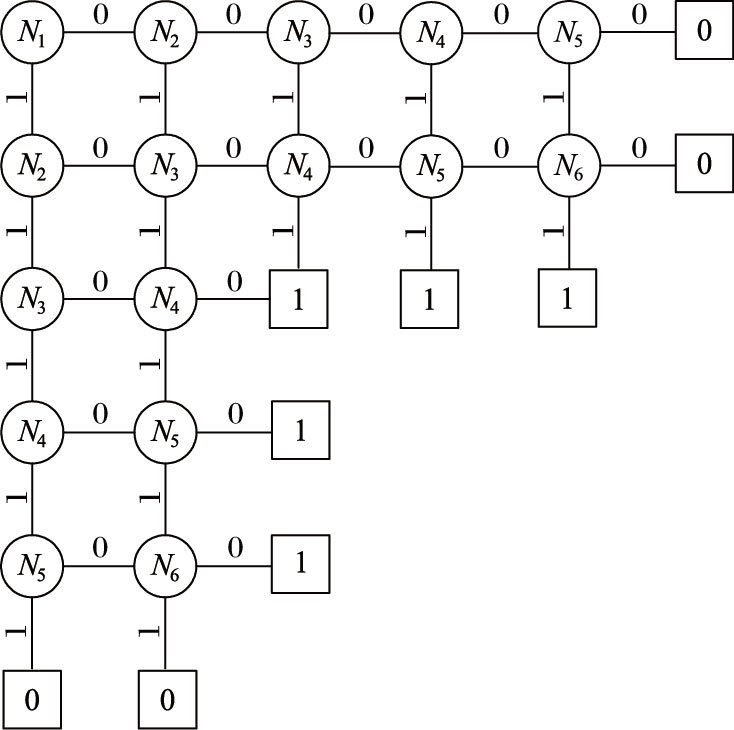
由表 2可知,2-to-4-out-of-6模型表示LM,该模型生成的BDD结构如图 2所示。
|
图 2 2-to-4-out-of-6模型的BDD结构 Figure 2 BDD for 2-to-4-out-of-6 model |
BDD结构中有两种叶子节点(正方形表示叶子节点):叶子节点“1”表示系统性能为LM,而叶子节点“0”表示系统性能不为LM,比如计算能力高于UBM或者低于LBM的情况。例如,当节点N1,N2,…,N5都处于0状态(故障状态),无论节点N6处于什么状态,系统的计算能力都低于LBM,即系统性能不为LM。这种情况下的路径与叶子节点“0”相连(如图 2中顶部的水平路径所示)。另一种情况,当节点N1,N2,…,N5都处于1状态(非故障状态),无论节点N6处于什么状态,系统的计算能力都高于UBM,即系统性能不为LM。这种情况下的路径也与叶子节点“0”相连(如图 2中最左侧的垂直路径所示)。
总之,对任何基于k-to-l-out-of-n结构的计算系统进行BDD建模,如果节点计算能力相同,那么BDD模型可以由以下引理推导得到:
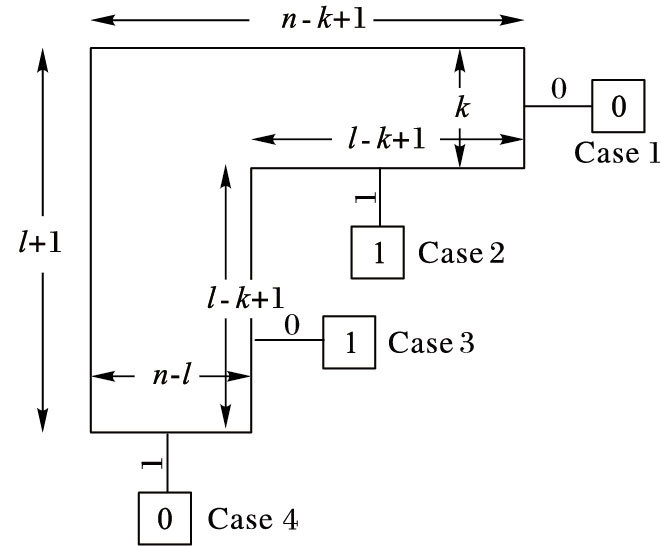
引理 基于k-to-l-out-of-n结构的计算系统,性能为Li时对应的BDD模型如图 3所示,即一个(l+1) *(n-k+1) 的矩阵去除右下角 (l-k+1) *(l-k+1) 的矩阵后剩余的部分。
|
图 3 基于k-to-l-out-of-n结构的BDD模型 Figure 3 BDD for k-to-l-out-of-n structure |
证明 在性能为Li的BDD模型中,即系统计算能力P的取值范围是[LBi,UBi],所有路径可以分为四种情况,每种情况的解释如下:
1) 如果超过n-k个节点处于0状态,无论其他节点处于什么状态,系统的计算能力都低于LBi,即系统性能不为Li。对应这种情况的路径和叶子节点“0”相连。
2) 如果超过n-l个节点处于0状态,并且至少有k个节点处于1状态,无论其他节点处于什么状态,系统的计算能力P都在 [LBi,UBi]中,即系统性能为Li。对应这种情况的路径和叶子节点“1”相连。
3) 如果超过k个节点处于1状态,并且至少有n-l个节点处于0状态,无论其他节点处于什么状态,系统的计算能力P都在 [LBi,UBi]中,即系统性能为Li。对应这种情况的路径和叶子节点“1”相连。
4) 如果超过l个节点处于1状态,不管其他节点处于什么状态,系统的计算能力都高于UBi,即系统性能不为Li。对应这种情况的路径和叶子节点“0”相连。
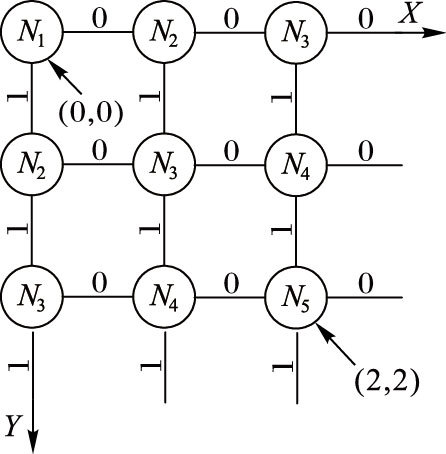
为了方便描述基于晶格结构的 k-to-l-out-of-n模型的BDD生成过程,将晶格结构置于二维坐标系中。如图 4所示,用坐标(x,y)表示非叶子节点的位置。如果一个BDD节点的坐标为(x,y),那么可以用“x+y+1”表示该节点的下标,例如表示为节点Nx+y+1。举例说明,坐标为(0,0) 的节点用N1表示,坐标为(2,2) 的节点用N5表示。
|
图 4 用坐标(x,y)表示的BDD结构 Figure 4 BDD structure represented by (x,y) |
基于k-to-l-out-of-n结构使用自顶向下算法进行BDD建模的代码描述如下:
BDD(k,l,n )=index=0; //首节点位置为0
For each y on vertical axis,0≤y≤l
If(y<k-1) //节点对应的y坐标值
//处理所有可能的x坐标值
For each x on horizontal axis,0≤x≤n-k
If(x=n-k); E=‘0’ //设置节点else-edge连接
Else E=index+1 //设置节点else-edge连接
T=index+n-k+1 //设置节点then-edge连接
create-BDD-node(x+y+1,E,T); //创建节点
index++; //更新节点位置
If(y=k-1)
For each x on horizontal axis,0≤x≤n-k
If(x<n-l); E=index+1; T=index+n-k+1
Else If (x<n-k); E=index+1; T=‘1’
Else E=‘0’; T=‘1’
create-BDD-node(x+y+1,E,T); index++;
If(k-1<y<l)
For each x on horizontal axis,0≤x≤n-l-1
If(x=n-l-1) ; E=‘1’
Else E=index+1
T=index+n-k+1
create-BDD-node(x+y+1,E,T); index++;
If(y=l)
For each x on horizontal axis,0≤x≤n-l-1
If(x=n-l-1) ; E=‘1’
Else E=index+1
T=‘0’
create-BDD-node(x+y+1,E,T); index++;
Return index
“create-BDD-node(x+y+1,E,T)”操作表示把一个新BDD节点添加到数组中。用index记录这个新节点在数组中的位置,新节点的编号为“x+y+1”。新节点的then-edge与一个BDD节点相连,数组中的T记录该BDD节点的位置index, else-edge与另一个BDD节点相连;数组中的E记录该BDD节点的位置index。3.3节中将对上述算法和传统算法进行性能比较,进一步说明上述算法的正确性。以下简要说明上述BDD生成算法的正确性:
如果一个BDD节点的坐标为(x,y),节点的then-edge和else-edge坐标计算如下:
1) y∈[0,k-1) ,x∈[0,n-k],每个节点的then-edge与编号为“x+y+2”并且坐标为(x,y+1) 的非叶子节点相连。如果x=n-k,那么这个节点的else-edge与叶子节点“0”相连;否则这个节点的else-edge与编号为“x+y+2”并且坐标为(x+1,y)的非叶子节点相连。
2) y=k-1,x∈[0,n-k]。如果x∈[0,n-l),那么这个节点的else-edge与编号为“x+y+2”并且坐标为(x+1,y)的非叶子节点相连,节点的then-edge与编号为“x+y+2”并且坐标为(x,y+1) 的非叶子节点相连;如果x∈[n-l,n-k),那么这个节点的else-edge与编号为“x+y+2”并且坐标为(x+1,y)的非叶子节点相连,节点的then-edge与叶子节点“1”相连;如果x=n-k,那么节点的else-edge与叶子节点“0”相连,节点的then-edge与叶子节点“1”相连。
3) y∈(k-1,l),x∈[0,n-l-1]。每个节点的then-edge与编号为“x+y+2”并且坐标为(x,y+1) 的非叶子节点相连。如果x=n-l-1,那么节点的else-edge与叶子节点“1”相连;否则,节点的else-edge与编号为“x+y+2”并且坐标为(x+1,y)的非叶子节点相连。
4) y=l, x∈[0,n-l-1]。每个节点的then-edge与叶子节点“0”相连。如果x=n-l-1,那么这个节点的else-edge与叶子节点“1”相连;否则,这个节点的else-edge与编号为“x+y+2”并且坐标为(x+1,y)的非叶子节点相连。
3.2 评估BDD模型在基于k-to-l-out-of-n结构的BDD模型中,计算每个BDD非叶子节点两个边的概率,就是计算该节点是处于非故障状态(then-edge)还是故障状态(else-edge)的概率,分别用1-Fj和Fj表示。
从根节点到叶子节点的每条路径都代表了一组节点的一个状态组合。如果到达叶子节点“1”,那么可以用这条路径或这个状态组合来表示系统性能Li。因此,系统处于性能Li就可以用从根节点到叶子节点“1”的所有路径的概率之和表示。
对性能为Li时生成的BDD模型,其性能评估可以通过以下递归算法表示。
| $\Pr (BDD)=(1-{{F}_{j}})\cdot \Pr (BDD.T)+{{F}_{j}}\cdot \Pr (BDD.E)$ | (6) |
其中:Fj表示BDD中根节点Ni处于故障状态的概率;Pr(BDD)表示BDD的概率;BDD.T是与根节点的then-edge相连的子BDD, BDD.E是与根节点的else-edge相连的子BDD。
评估BDD模型的递归算法,代码如下:
Evaluate(BDD)=
If(BDD=‘1’); // 若BDD节点是叶子节点“1”
Return 1
If(BDD=‘0’);// 若BDD节点是叶子节点“0”
Return 0
If(BDD.Pr has been computed); // 若已经计算过
Return BDD.Pr // 按照式(6) 计算
BDD.Pr=(1-Fj)*Evaluate(BDD.T)+Fj*Evaluate(BDD.E)
Return BDD.Pr
递归算法的结束条件是,如果BDD节点是叶子节点“0”,那么Pr(BDD)=0;如果BDD节点是叶子节点“1”,那么Pr(BDD)=1。
对于第2章给出的实例系统,其节点具有相同计算能力,表 3给出了实例系统性能分析的结果,BDD模型的大小用非叶子节点的数量表示。
| 表 3 实例系统性能分析结果 Table 3 Performance analysis results of example system |
为了证明自顶向下BDD生成算法的有效性和正确性,将其与传统BDD生成算法作比较。传统BDD生成算法一般采用自底向上算法[11-15],首先创建与系统性能状态对应的节点状态布尔表达式,然后根据所给的逻辑操作自底向上组合生成BDD。为了防止相同表达式的重复构建,使用哈希表computation-table将一个布尔表达式映射到一个BDD节点。只有当computation-table中没有相应的布尔表达式记录时,才执行表达式BDD构建。但是,尽管使用computation-table,在自底向上的组合过程中,仍会产生大量BDD中间节点。
为了比较性能,使用2-to-5-out-of-n模型作为基准系统,n=10,11,12,13,14,15,节点的故障模型为负指数分布模型。所有计算都在一台PC上完成,其CPU为Intel Core i7- 2600 3.40 GHz,内存为2.00 GB,运行Windows 7操作系统。性能比较结果如表 4所示。注意,BDD的构造时间以毫秒(ms)为单位,BDD的大小用非叶子节点的数量表示。实验数据表明,自顶向下BDD生成算法比传统自底向上BDD生成算法更高效,而且随着系统规模的增加,更能体现这样的优势。自顶向下BDD生成算法使用特殊的晶格结构,不会产生任何冗余的中间节点,由表 4中相同的“中间BDD节点数”和“最终BDD节点数”得以证明。
| 表 4 两种BDD生成算法性能比较结果(2-to-5-out-of-n) Table 4 Performance comparison results of two BDD generation algorithms (2-to-5-out-of-n) |
为了进一步说明自顶向下BDD生成算法的性能优势,使用一个更大的k-to-l-out-of-n模型作为基准系统,n=50,60,70,80,90,100,每个节点的状态分布随机生成;考虑三组不同的(k,l)组合。
表 5中BDD分析时间包括构建BDD的时间和评估BDD的时间。数据表明,自顶向下BDD生成算法可以快速地分析基于k-to-l-out-of-n结构的大型计算系统,并且BDD大小和分析时间的增长较为缓慢。特别是BDD的规模复杂度接近n2/3的情况,由表 5数据可知,随n值的增大,BDD大小增长缓慢。
| 表 5 BDD大小与分析时间对比 Table 5 Comparison of BDD size and analysis time |
本文提出了一种新的基于BDD的集群计算系统性能分析方法,该方法能够有效处理节点计算能力相同的大型集群计算系统性能分析问题。采用自顶向下BDD生成算法可以避免产生大量中间操作,充分利用特殊的k-to-l-out-of-n结构,相比传统的自底向上生成算法更为高效。
处理节点不同且计算能力也不同的集群系统性能分析问题时,适合使用状态空间法,如Markov模型。但是,对中型或大型集群计算系统进行性能分析时,这些方法会出现“组合爆炸”问题,而且受限于可积故障时间分布[16-17]。最近,针对部件不同且相互独立的多状态k-out-of-n系统,我们在文献[18中提出了一种基于决策图的方法。决策图方法与Markov方法不同,Markov方法使用一个显式状态转换图模型,而决策图使用一个组合模型,它用不相交路径表示不相交节点的状态组合,这些状态组合使整个系统处于一个特定性能状态。实例结果表明,决策图方法可以有效地处理大量实际问题,但这个方法只适用于k-out-of-n模型,并不适用本文中的k-to-l-out-of-n模型。要将基于决策图的方法应用于k-to-l-out-of-n模型中,需要实现新的模型生成算法、新的简化规则以及新的排序策略。
虽然在k-to-l-out-of-n系统的建模和分析方面已经有了一些研究成果,但是本文提出的新方法在大型集群计算系统性能分析方面仍具有一定意义,特别是在现代数据中心和云计算系统规模快速增长的情况下。以后我们还将继续扩展基于BDD的性能分析方法,将其应用于具有多状态节点的大型集群计算系统。
| [1] | FOSTER I, KESSELMAN C, TUECKE S. The anatomy of the grid:enabling scalable virtual organizations[J]. The International Journal of High Performance Computing Applications:Information for Contributors, 2001, 15 (3) : 200-222. doi: 10.1177/109434200101500302 |
| [2] | VOUK M A. Cloud computing-issues, research and implementations[J]. Journal of Computing and Information Technology, 2008, 16 (4) : 235-246. doi: 10.2498/cit.1001391 |
| [3] | MO Y. Variable ordering to improve BDD analysis of phased-mission systems with multimode failures[J]. IEEE Transactions on Reliability, 2009, 58 (1) : 53-57. doi: 10.1109/TR.2008.2011673 |
| [4] | HARISH P, NARAYANAN P J. Accelerating large graph algorithms on the GPU using CUDA[C]//HiPC 2007:Proceedings of the 14th International Conference on High Performance Computing, LNCS 4873. Berlin:Springer-Verlag, 2007:197-208. |
| [5] | SHIVA S G. Advanced Computer Architectures[M]. Boca Raton, FL: CRC Press, 2005 : 312 -322. |
| [6] | MO Y, XING L, ZHONG F, et al. Choosing a heuristic and root node for edge ordering in BDD-based network reliability analysis[J]. Reliability Engineering and System Safety, 2015, 131 : 83-93. |
| [7] | LEVITIN G, XING L. Reliability and performance of multi-state systems with propagated failures having selective effect[J]. Reliability Engineering and System Safety, 2010, 95 (6) : 655-661. doi: 10.1016/j.ress.2010.02.003 |
| [8] | ANDREWS J D. To not or not to not[C]//ISSC-2000:Proceedings of the 18th International System Safety Conference.[S.l.]:System Safety Society, 2000:267-275. |
| [9] | RAUZY A, DUTUIT Y. Exact and truncated computations of prime implicants of coherent and non-coherent fault trees within aralia[J]. Reliability Engineering and System Safety, 1997, 58 (2) : 127-144. doi: 10.1016/S0951-8320(97)00034-3 |
| [10] | MO Y, XING L, ZHONG F, et al. Reliability evaluation of network systems with dependent propagated failures using decision diagrams[J]. IEEE Transcations on Dependable and Secure Computing, 2015, 13 (6) : 672-683. |
| [11] | MEYER J F. Model-based evaluation of system resilience[C]//DSN-W 2013:Proceedings of the 201343rd Annual IEEE/IFIP Conference on Dependable Systems and Networks Workshop. Washington, DC:IEEE Computer Society, 2013:1-7. |
| [12] | RAUZY A B, GAUTHIER J, LEDUC X. Assessment of large automatically generated fault trees by means of binary decision diagrams[J]. Proceedings of the Institution of Mechanical Engineers, Part O:Journal of Risk and Reliability, 2007, 221 (2) : 95-105. doi: 10.1243/1748006XJRR47 |
| [13] | POCKY M, MALASS E, WALTER M. Combining different binary decision diagram techniques for solving models with multiple failure states[J]. Proceedings of the Institution of Mechanical Engineers, Part O:Journal of Risk and Reliability, 2011, 225 (1) : 18-27. doi: 10.1177/1748006XJRR284 |
| [14] | MO Y, ZHONG F, LIU H, et al. Efficient ordering heuristics in binary decision diagram-based fault tree analysis[J]. Quality and Reliability Engineering International, 2013, 29 (3) : 307-315. doi: 10.1002/qre.1382 |
| [15] | MEYER J F. Defining and evaluating resilience:a performability perspective[C/OL]//PMCCS-9:Proceedings of the 9th International Workshop on the Performability Modeling of Computer and Communication Systems.[S.l.]:Mendeley, 2009[2016-03-06]. http://ftp.eecs.umich.edu/people/jfm/PMCCS-9_Slides.pdf. |
| [16] | REIBMAN A, TRIVEDI K. Numerical transient analysis of Markov models[J]. Computers and Operations Research, 1998, 15 (1) : 19-36. |
| [17] | TRIVEDI K S. Probability and Statistics with Reliability, Queuing and Computer Science Applications[M]. Upper Saddle River, NJ: Prentice Hall, 2001 : 172 -179. |
| [18] | MO Y, XING L, AMARI S V, et al. Efficient analysis of multi-state k-out-of-n systems[J]. Reliability Engineering and System Safety, 2015, 133 : 95-105. doi: 10.1016/j.ress.2014.09.006 |




