随着移动互联网技术与地理定位技术的发展,基于位置的服务当下被广泛应用于交通、物流、旅游等多个领域。在众多基于位置的服务中,地图服务是一项极为常见的服务。根据位置信息为用户在路网空间中查询一条合适的路径是地图服务的一项重要功能[1]。考虑到在Web资源与地图服务结合的背景下,路径查询功能应不再局限于在给定起点与终点的情况下单纯返回两点间最短路径。为满足用户个性化的行程需求,针对特殊路径,提出高效的查询方法尤为重要。
在生活中可以考虑如下场景:用户来到了一个陌生的城市,希望搜寻一条最受欢迎的旅游路线,该路线从指定起点出发,途经所有与用户指定关键词相关的兴趣点(如自然景区、文化古迹、特色美食),最终到达用户指定的终点,此外路径需满足游客有限的行程预算。
该类路径查询问题被定义为基于关键词的最优路径查询(Keyword-aware Optimal Route Search,KORS)[2-3]。KORS是空间关键词查询中的一类特殊查询[4],能够为地图服务在旅游行程中的路线规划提供有效支持。与传统的单源最短路径(Single Source Shortest Path)查询不同,KORS综合考虑路径关键词覆盖条件、路径行程代价约束以及路径流行度三类因素间的组合优化性,该类问题为NP-hard问题[2],实际路径的搜索空间复杂度为O(dn)(d为图中顶点最大出度)。
目前针对KORS算法主要基于邻边拓展的路径构建策略,该策略自起点出发通过不断拓展当前路径终点的所有邻边以产生新的子路径,直到路径到达查询终点。该过程实际枚举了起点与终点间所有可行路径,由于在KORS的问题求解中,关键是通过路径拓展构建满足查询约束的可行路径,因此当查询关键词个数较多、起点终点间最优路径的顶点个数较多或者部分查询关键词分布稀疏时,邻边拓展的路径构建策略将枚举大量的中间路径,造成算法在空间、时间上开销骤增,可扩展性变差。
为解决上述问题,本文提出基于关键词序列的路径构建 (Keyword Sequence Route Generating,KSRG)算法。该算法提出基于关键词序列的路径构建方案,在路径拓展过程中优先考虑路径对查询关键词的包含情况,采用关键词引导下的有效路径拓展代替盲目的邻边拓展,避免无关顶点的遍历,提高候选路径的构建效率;其次采用完全多项式时间近似策略,以及在查询中对无效中间结果的及时裁剪,对问题解进行近似求解,从而将搜索空间复杂度模限定在多项式级,提升算法可扩展性。综上所述,本文的主要工作总结如下:
1) 针对KORS提出基于关键词序列路径构建算法——KSRG算法,在路径拓展过程中优先满足查询关键词的全包含条件,对查询结果进行高效的近似求解;
2) 运用四组图数据集,对各类算法进行充分实验测试,并对查询效率进行对比,验证本文算法的有效性以及相对现有算法在查询性能上的提升效果。
1 相关工作 1.1 空间关键词查询近年来学者们针对空间关键词查询的研究[5-8]提出了多种查询,如:最优k邻居查询(top-kNN)、范围查询(Range query)、逆向最邻近查询(Reverse kNN query),这些查询对空间对象的空间邻近度与文本相似性进行考察,但查询粒度局限为单一个体,无法解决多个邻接的空间对象组合相连下最优路径问题。文献[6]在欧氏空间中提出了满足关键词全包含下的一组邻近空间实体集合的查询;文献[9]在路网空间下进行最优子区域的高效查询。上述查询返回一组兴趣点集合,但无法适用于路径形式下的组合优化问题。
1.2 最优路径查询最优路径查询是基于位置的服务中被广泛研究的一个问题[2-3, 10-13]。文献[10]于空间数据库领域最先提出一种新的行程规划查询(Trip Plan Query,TPQ),TPQ在指定的空间两点间搜索一条经过所有指定类别对象且长度最小的路径,如在用户的住处与工作地点间查找一条经过便利店、加油站、银行的最短路径,该类查询问题为广义旅行商问题(Generalized Traveling Salesman Problem,GTSP)的特例,为NP难题。与TPQ问题类似,文献[11]提出最优序列路径 (Optimal Sequenced Route,OSR)查询问题,搜索一条由空间中某点出发,按规定类别访问顺序,经过所有类别对象且长度最短的路径,如从用户当前所在位置出发找到一条依次经过银行、加油站、影院的最短路径,该查询固定了对象的访问顺序,为TPQ问题的一类特例。文献[12]提出了多规则局部有序路径(Multi-Rule Partial Sequenced Rout,MRPSR)查询,该查询区别于OSR查询中固定的类别访问顺序,仅对部分不同对象的访问顺序限定条件,如用户必需在访问加油站前优先访问银行。文献[13]提出BBS(Batch Backward Search)与SBS(Simple Backward Search)两类算法解决任意访问规则下的最优路径查询问题,相比文献[12]可满足更为多样的访问约束。文献[14]在旅游背景下提出体验式路径查询(Short-term Experience Route Search,SERS)。文献[15]基于贪婪策略提出了三种高效的旅游行程规划算法,折中游客行程预算与景点流行度,返回一条近似最优行程路径。
在TPQ、OSR、MRPSR查询以及SERS中,对象类别属性较为单一,包含信息量有限,使得路径难以精确匹配用户个性化要求。此外由于上述路径查询忽略了路径代价预算,因此不能较好地满足实际生活场景中的行程问题。文献[15]虽然考虑了路径行程中各类预算条件的满足,但路径中兴趣点的选择较为固定,无法适应不同用户的多种个性化要求。
1.3 KORS为使规划的路线能够满足用户个性化行程需求,同时在代价预算上保持合理性,基于关键词下的最优路径查询(KORS)是一种合适的查询类型。该查询最早在文献[2]中被提出,与欧氏空间下的路径问题[10-12]不同,KORS在路网空间下查询返回一条覆盖所有用户指定关键词,同时满足行程预算(如费用、时间)且流行度最大的路径。该类路径问题为权值受限最短路径(Weight Constrained Shortest Path,WCSP)问题的一个特例,为NP难题[2]。基于邻边拓展的路径构建策略,OSScalling和BucketBound算法[2-3]实现了多项式复杂度下的问题近似求解。然而由于路径拓展策略,算法在大规模的无向图以及多关键词条件下进行时,存在复杂度过高、空间开销极大、伸缩性不理想的缺陷。
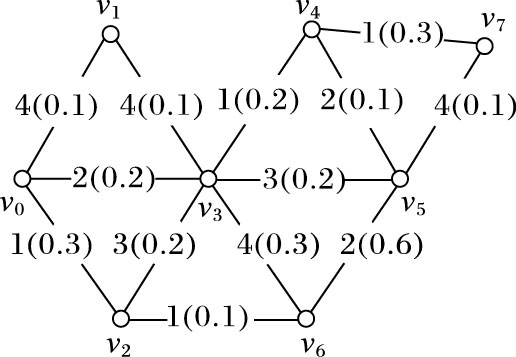
2 问题定义 2.1 问题抽象将旅游行程抽象为如图 1所示的一幅连通图G=(V,E)。图G中,顶点集V中每个顶点v代表了一个兴趣点。v拥有两类属性:1) 地理位置坐标〈经度,纬度〉,符号表示为v.loc;2) 关键词集合,〈关键词1,关键词2,关键词3…〉(个数不大于5) ,符号表示为v.ψ。图 1中各个顶点所带的关键词信息如表 1所示。
|
图 1 图的结构 Figure 1 Structure of graph |
| 表 1 顶点关键词信息 Table 1 Information of vertex keyword |
边集E中的每条边表示连接两处兴趣点的直通行程e。e带有两类权值:1) 代价权值(图中括号外的数值),表示通过该行程所需的行程代价(根据不同场景可为路段的时耗或距离);2) 流行度权值(图中括号内的数值),表示该行程的流行度。若vi到vj存在直达路段(vi,vj)∈E,则b(vi,vj)为边的代价权值,p(vi,vj)为边的价值权值。
r=(v0,v1,…,vn-1,vn)表示顺序经过若干连续相邻的兴趣点,由v0达到vn的路径。路径的代价定义为路径包含的所有边的代价权值和,即为:$\sum\limits_{i=1}^{n}{b({{v}_{i-\text{1}}},{{v}_{i}})}$,符号表示为BS(r)。
根据文献[16]中定义,路径的流行度BS(r)为路径上所有边的流行度权值的乘积,即为:$\underset{i=1}{\overset{n}{\mathop \prod }}\,p({{v}_{i-\text{1}}},{{v}_{i}})$。
路径r的关键词为其上所有兴趣点关键词集合并集,即为:$r.\psi =\bigcup\limits_{v\in R}{v.\psi }$。
在KORS应用场景中,最优路径查询Q=(vs,vt,ψ,Δ)包含四类查询参数,其中:vs为用户指定的行程起点(可为图 1任意某个兴趣点);vt代表用户指定的行程终点;ψ表示一组用户指定的关键词集合;Δ表示路径代价上限值。
将由起点vs至终点vt的路径集合表示为Rs,t,根据查询Q中参数,若某路径r∈Rs,t且满足:1) BS(r)<Δ;2) r.ψ⊇Q.ψ,则路径r为一条可行路径,所有可行路径的集合表示为R,KORS的最优路径符号表示为ropt,ropt即为可行路径集合R中拥有最大流行度的路径。具体形式化描述如下:
| $\left\{ \begin{array}{*{35}{l}} R=\{r|r\in {{R}_{s,t}}\wedge r.\psi \supseteq Q.\psi \wedge BS(r)<\Delta \} \\ {{r}_{opt}}=\underset{r\in R}{\mathop{\arg }}\,\max PS(r) \\ \end{array} \right.$ |
由于路径流行度与边流行度权值的计算关系为$PS(r)=\prod\limits_{i=1}^{n}{p({{v}_{i-\text{1}}},{{v}_{i}})}$,且要求最优路径应有尽可能大的流行度,因此对图上每条边赋予第三类权值:目标权值,符号表示为o(vi,vj),目标权值与流行度权值的关系如下:
| $o\left( {{v}_{\text{i}}},{{v}_{j}} \right)=\text{log}\left( 1/p\left( {{v}_{\text{i}}},{{v}_{j}} \right) \right)$ | (1) |
log底数可为任意大于1的值,路径R的目标值定义为路径上所有边的目标权值之和,即为:$\sum\limits_{i=1}^{n}{o({{v}_{i-\text{1}}},{{v}_{i}})}$,符号表示为OS(r)。
定理1 在图G中拥有最大流行度BS(r)的路径,拥有最小目标值OS(r)。
证明 由于路径目标值$OS(r)=\sum\limits_{i=1}^{n}{o({{v}_{i-\text{1}}},{{v}_{i}})} $,且边的目标权值与流行度权值间有式(1) 所示的转化关系,因此满足:
| $OS(r)=\log \left( 1/\prod\limits_{i=1}^{n}{p({{v}_{i-\text{1}}},{{v}_{i}})} \right)$ | (2) |
由于$PS(r)=\prod\limits_{i=1}^{n}{p({{v}_{i-\text{1}}},{{v}_{i}})}$,则有OS(r)=log(1/BS(r))。故当BS(r)取得最大值时,OS(r)有最小值。
证毕。
根据定理1,KORS所求最优路径ropt即为满足查询约束条件,且拥有最小目标值的路径,形式化描述为:
| $\left\{ \begin{array}{*{35}{l}} R=\{r|r|r\in {{R}_{s,t}}\wedge r.\psi \supseteq Q.\psi \wedge BS(r)<\Delta \} \\ {{r}_{opt}}=\underset{r\in R}{\mathop{arg}}\,\min OS(r) \\ \end{array} \right.$ |
为在算法执行中及时过滤无效的中间结果,提高问题求解效率,在算法执行前,需进行如下准备工作。
工作1 路径预处理。为在搜索过程中对局部路径的后续拓展情况作预判,及时去除不满足约束条件的中间结果,采用弗洛伊德算法[17]对图G中任意两点求其间拥有最小OS(r)与最小BS(r)的路径,两类特殊路径符号表示为τi,j、σi,j。
工作2 构建倒排索引。抽取图G中各兴趣点的所有关键词构成一非重关键词集合。该集合中每个关键词对应一个倒排表,记录包含该关键词的兴趣点的集合。通过倒排索引的构建,含有查询关键词的兴趣点可被优先筛选。
3.2 算法描述KSRG算法首先采用关键词序列路径构建来提高可行路径构建效率,此基础上通过完全多项式时间近似策略进一步实现高效、可扩展性更优的KORS。以下首先对这两部分进行说明。
3.2.1 KSRG预备知识KSRG核心在于路径拓展过程中优先满足查询关键词的全包含条件,进行关键词引导下的路径拓展。在阐述思路前,有如下定义陈述。
定义1 关键词顶点。给定查询Q=(vs,vt,ψ,Δ),关键词ti∈ψ。若vm.ψ包含ti,且BS(σs,m)+BS(σm,t)<Δ,则vm为关键词ti对应的关键词顶点,ti对应的所有关键词顶点构成的集合符号表示为Vti。
定义2 关键词路径。关键词ti∈vm,关键词tj∈vn,路径r∈Rm,n,若OS(r)=OS(τm,n),则路径r为一条关键词路径。
定义3 关键词顶点序列。给定查询Q=(vs,vt,ψ,Δ),其中ψ=〈ti1,ti2,…,tin〉,对于某条包含所有查询关键词且满足代价约束的可行路径r,根据每个查询关键词在路径r拓展过程中被先后覆盖到的顺序(仅考虑每个关键词在路径中第一次被覆盖的次序),可得关键词覆盖序列st=〈ts1,ts2,…,tsn〉,满足该序列的关键词顶点序列为sv=〈vs1,vs2,…,vsn〉(vs1∈Vts1,vs2∈Vts2,…,vsn∈Vtsn)。
定义4 关键词序列路径。若路径r的关键词顶点序列中所有相邻关键词顶点间的子路径为关键词路径,则路径r为关键词序列路径(Keyword Sequence Route,KSR)。关键词序列路径的目标值为其中所有关键词路径的目标值之和,即为:$OS(r)=\sum\limits_{i=1}^{n-1}{OS({{\tau }_{{{s}_{i}},{{s}_{i+1}}}})}$。在所有满足查询条件的KSR集合中将拥有最小目标值的KSR表示为KSRopt,则有如下定理。
定理2 $OS(KS{{R}_{opt}})<|\psi |OS({{r}_{opt}})$,其中|ψ|为查询关键词个数。
证明 将忽略Δ,给定新查询Q′=(vs,vt,ψ),文献[10]基于贪婪策略提出AMD算法可对一条包含ψ中所有关键词且有最短长度的路径rmin进行近似求解,令近似求解得的路径符号为rMD,若将路径长度作为路径目标值,则有OS(rMD)<|ψ|OS(rmin)[10]。由于rMD为KSR,故有OS(KSRopt)<OS(rMD),同时OS(rmin)<OS(ropt)最终得OS(KSRopt)<OS(rMD)<|ψ|OS(ropt)。
证毕。
根据定理2,采用KSRG对KORS的最优路径ropt进行近似求解,基本思想为:根据查询关键词集,枚举该集合下各个关键词覆盖序列对应的可行关键词顶点序列,计算其对应的关键词序列路径的目标值。在所有满足查询约束的可行关键词路径中,拥有最小目标值的路径即为最优路径ropt。
3.2.2 完全多项式时间近似策略在3.2.1节中,枚举所有关键词顶点序列依然是一项复杂度较大的工作。给定一个查询,查询关键词为Q.ψ,该工作的复杂度为O(nk×k!)(其中k=|Q.ψ|,n=max{|Vtm||tm∈Q.ψ})。
为避免此类复杂度下的问题求解,采用完全多项式时间近似策略(Fully Polynomial-Time Approximation Scheme,FPTAS)[18-19],通过相关变量转化,可将问题求解的规模转变为多项式级,具体步骤如下所述。
首先定义比例因子
θ=(εmin{OS(τi,j)}min{BS(σi,j)})/Δ
其中:min{OS(τi,j)}为图G中任意两点间的最小路径目标值,min{BS(σi,j)}为任意两点间最小路径代价值,ε为一范围在0到1之间的关联参数。利用θ对图中任意两点间的目标值最优路径τi,j的路径目标值OS(τi,j)进行转换,生成修正目标值OS′(τi,j),两者转化关系为:OS′(τi,j)= θ-1OS(τi,j)」。对于某一关键词顶点序列符号表示为sv=〈vs1,vs2,…,vsn〉,对应的关键词序列路径r,则其修正目标值为$OS'(r)=\sum\limits_{i=1}^{n-1}{OS'({{\tau }_{{{s}_{i}},{{s}_{i+1}}}})}$。
在KSRG构建策略中,路径由起点vs出发,通过关键词路径拓展至所有之前未被包含的关键词对应的关键词顶点,产生更长关键词序列对应的关键词序列路径;所有子路径继续由当前拓展终点重复上述拓展步骤直到路径关键词序列包含所有查询关键词。考虑到在路径拓展过程需记录下所有枚举的局部路径,因此需以适当方式表示这些中间结果。
定义5 路径标签。将由起点vs出发拓展至某一关键词顶点vi的路径记录为一个四元组形式下的路径标签Lin,具体格式为(λ,OS′,OS,BS)。其中:λ表示路径当前覆盖的查询关键词,OS′为该路径的修正目标值,OS为路径原始的目标值,BS为路径的代价值。定义OSL(Lin)=OS(Lin)+OS(τi,t),表示当前路径进行后续拓展至vd的最小路径目标值,定义BSL(Lin)=BS(Lin)+BS(σi,t)为路径后续拓展至vd的最小路径代价值。每个关键词顶点维护一个标签列表vi.list,保存拓展至当前点vi的所有局部路径。从vs出发至关键词顶点vi的路径有多条,这将导致vi.list存储过多路径标签,使算法存储开销过大。然而,在这些中间路径中往往存在大量无效路径。
定义6 无效标签。将由vs至vi的第m条及n条路径表示为rim、rin,对应的路径标签为Lim、Lin。当且仅当如下三种条件同时成立认为Lin相对Lim为无效标签:
1) Lin.λ⊆Lim.λ;
2) Lin.OS′≥Lim.OS′;
3) Lin.BS≥Lim.BS。
若Lim为无效标签,则将不会被加入vi.list中,即vi.list仅保存当前有效路径标签。在KSRG中,路径拓展的实现具体由标签操作完成,标签操作定义如下所述。
定义7 标签操作。若当前拓展到某一关键词顶点vi的路径对应的路径标签为Lim,针对Lim.λ中尚未包含的查询关键词对应的所有关键词顶点vj,路径由τi,j拓展至关键词顶点vj。根据Lim创建新路径标签Ljn,两者具体关系为:
1) Ljn.λ=Lim.λ∪(vj.ψ∩Q.ψ);
2) Ljn.OS′=Lim.OS′+OS′(τi,j);
3) Ljn.OS=Lim.OS+OS(τi,j);
4) Ljn.BS=Lim.BS+BS(τi,j)。
针对标签操作产生的大量中间结果(路径标签)根据一定的优先级,可决定哪条路径标签优先进行下一步拓展,使路径拓展尽可能朝最优解所在方向推进,具体规则如下定义。
定义8 标签优先级。综合路径标签中的λ、OS′和BS三部分判定标签优先级:
1) 当两条路径对应的路径标签包含的查询关键词个数不同时,包含查询关键词个数越多的路径,其优先级越高;
2) 当两条路径对应的路径标签中包含的查询关键词个数相同时,路径目标值越小,路径优先级越高;
3) 当两条路径对应的路径标签包含的查询关键词个数、路径目标值都相同时,路径代价值越小路径优先级越高。
定理3 KSRG路径拓展过程中,有效标签个数的上界为:
| $k{{V}_{\max }}\times {{2}^{k}}\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \left\lfloor \frac{\max \{OS({{\tau }_{i,j}})\}\Delta }{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $ |
其中:Vmax为查询关键词中单个关键词对应的最大关键词顶点个数,k为查询关键词个数。
证明 由于路径标签四元组中OS′、OS相对应,且根据定义6对无效标签裁剪,因此在λ、OS′固定后,BS仅保存当前最小取值,故有效标签上界个数仅与λ、OS′的组合数有关,给定k个查询关键词,λ最多有2k种可能情况;给定查询代价约束Δ,则KSRG中关键词路径拓展的次数不超过$\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $,综合比例因子θ定义公式,因此OS′上界为$\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \left\lfloor \frac{\max \{OS({{\tau }_{i,j}})\}\Delta }{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $,因此单个关键词顶点的有效标签枚举量上界为:
| ${{2}^{k}}\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \left\lfloor \frac{\max \{OS({{\tau }_{i,j}})\}\Delta }{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $ |
令所有关键词顶点的集合表示为Vkw,由于$\left| {{V}_{kw}} \right|\text{=}\sum\limits_{{{t}_{i}}\in \psi }{|{{V}_{{{t}_{i}}}}|}<k{{V}_{\max }}$,因此算法在KSRG路径拓展中有效标签枚举总量的上界为:
| $k{{V}_{\max }}\times {{2}^{k}}\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \left\lfloor \frac{\max \{OS({{\tau }_{i,j}})\}\Delta }{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $ |
根据定理2,KORS求解的复杂度与Δ呈多项式相关性,与k呈指数相关性(k的取值通常不大)。
3.2.3 算法步骤综合3.2.1节与3.2.2节中各项定义和定理,提出KSRG算法。算法的基本思想为枚举各关键词序列下的有效路径标签:首先筛选各个查询关键词对应的所有关键词顶点,之后路径由起点vs出发按关键词序列进行关键词路径拓展,产生包含更多查询关键词的关键词序列路径,在此过程中每次选择优先级最高的中间路径进行拓展,并及时检查拓展所得路径裁剪无效路径标签。重复此过程直到产生所有终点vt对应的包含全部查询关键词的路径标签,筛选满足查询约束且有最小修正目标值的路径标签,即为最优路径ropt。具体描述如下:
算法1 KSRG算法。
输入 图G,查询Q=(vs,vt,ψ,Δ);
输出 最优路径标签LL。
1) 初始化队列Q为空队列,LL为Null,上界值U为无穷大;
2) 获取Q.λ中每个关键词ti对应的Vti;
3) 初始化标签Ls0=(vs.ψ∩Q.ψ,0,0,0) ,加入Q;
4) While Q中元素不为空 do
5) 取Q中优先级最高的路径标签Lik;
6) For each ti∈Q.ψ-Lik.ψ do
7) For each vj∈Vti do
8) Ljn=标签操作(Lik,vj);
9) If OSL(Ljn)>U or BSL(Ljn)>Δ then
10) discard Ljn //舍弃该路径,即停止后续拓展
11) Else
12) checkRelation(Ljn,vj);
13) If Ljn为无效标签 then
14) discard Ljn //无效路径被舍弃,即停止后续拓展
15) Else
16) If Q.ψ⊄Ljn then
17) Ljn加入vj标签列表,加入队列Q;
18) 删除Q中相关无效标签;
19) Else
20) If Ljn.BS+BS(τj,t)<Δ then
21) U=Ljn.OS+OS(τj,t);
22) LL=标签操作(Ljk,vt);
23) Return LL;
算法1中第1) ~3) 行为初始化工作,队列Q按定义8中优先级对所有中间结果(路径标签)进行顺序存储。在获取各个查询关键词对应的关键词顶点集合后,关键词序列路径由起点vs开始拓展。第4) ~22) 行为关键词序列下的关键词路径拓展:当队列Q非空时,选取队列中优先级最高路径标签,通过关键词路径将其拓展至所有含有尚未包含的关键词对应的关键词顶点(第4) ~第8) 行);对于所有拓展得到的路径标签Ljn,若其OSL(Ljn)>U或BSL(Ljn)>Δ,则该路径的后续拓展必定无法产生满足条件的结果,停止该路径拓展(第9) ~10) 行);否则进行标签检查(第11) ~12) 行),标签检查函数checkRelation(Ljn,vj)将Ljn与vj.list中所有标签进行比较,判断标签有效性并删除无效标签,详细如下。
标签检查函数 checkLabel。
输入 路径标签Ljn,vj;
输出 布尔值flag。
① 初始化布尔值flag=false,无效标签表UL;
② For each l∈vj.list do
③ If Ljn相对l为无效标签 then
④ flag=true;
⑤ return flag;
⑥ If l相对Ljn为无效标签 then
⑦ 将l加入UL;
⑧ list中删除l;
⑨ Return flag;
若Ljn经标签检查函数检测为无效标签,则Ljn停止后续拓展(第13) ~14) 行);对于有效标签Ljn,若Ljn未包含所有查询关键词则还需进行后续拓展,将Ljn加入队列Q(第15) ~18) 行);若Ljn包含所有关键词则检查由Ljn对应路径经τj,i至vt的路径是否满足代价约束,同步更新目标值上界U,最优路径标签LL(第19) ~22) 行);最终当队列Q中元素为空时,即完成所有关键词序列路径拓展,返回LL即为所求结果(第23) 行)。
算法运行示例:查询图以图 1为例,设查询具体为$\theta =\frac{0.5*{{b}_{\min }}*{{o}_{\min }}}{10}=\frac{0.5*1*\log (1/0.6)}{10}=\frac{1}{20}(\log 5-\log 3)$。起点初始化路径标签为L00=(∅,0,0,0) ,由于未包含查询关键词t1、t2、t3,因此该轮路径拓展中通过关键词路径直接拓展至t1或t2或t3对应的关键词节点(v1,v2,v3,v5,v6,v7),分别产生新路径标签L10=(t3,90,1,4) ,L20=(t2,47,0.52,4) ,L30=(t1,63,0.7,2) ,L50=(t2,126,1.4,5) ,L60=(t1,110,1.22,2) ,L70=(t3,216,2.4,9) 加入队列Q。
取队列Q中最高优先级标签L210进行第二轮拓展,由于L20未包含t1、t3,因此在该轮拓展中,可通过关键词路径直接拓展至 t1或 t3对应的关键词节点(v1,v3,v6,v7)产生新路径标签L1=({t2,t3},137,1.52,6) ,L31=({t1,t2},110,1.2,4) ,L61=({t1,t2},137,1.52,2) ,L71=({t2,t3},173,1.92,6) ,由于BSL(L11)>10,因此除L11外将新产生的标签加入队列Q。
取队列Q中最高优先级标签L31进行第三轮拓展,由于L31未包含t3,因此在该轮拓展中通过关键词路径直接拓展至 t3对应的关键词节点v7,此时由于产生新路径标签L72=({t1,t2,t3},220,2.44,6) 包含所有查询关键词,故为一可行解,将LL标记为L72,U标记为2.44。
继续拓展迭代直到队列Q为空,最终得到最优解为L72,因此最优路径ropt={v0,v2,v4,v7}。
3.2.4 算法分析复杂度分析 根据定义6,由于无效标签的裁剪,每个关键词顶点在算法中最多产生Lmax个有效标签,其中 Lmax=${{2}^{k}}\left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \left\lfloor \frac{\max \{OS({{\tau }_{i,j}})\}\Delta }{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor $, 同时所有关键词顶点的总数$V=\sum\limits_{{{t}_{i}}\in \psi }{|{{V}_{{{t}_{i}}}}|}<k{{V}_{\max }}$(Vmax为最大关键词顶点个数,k为查询关键词个数),故算法最多累积产生kVmaxLmax个路径标签。一次while循环对应一个优先度最高的路径标签出列,在最坏情况下算法while循环总次数为kVmaxLmax;每次while循环中最多产生kVmax个路径标签,每产生一个路径标签需进行若干次标签检查(复杂度为O(Lmax)),以及标签入列操作(复杂度为O(lg(Lmax))),因此一次while循环下的复杂度为O(kVmax(Lmax+lg(Lmax)))。故算法累计复杂度为O(k2Vmax2Lmax2+k2Vmax2Lmaxlg(Lmax))。OSScalling、BucketBound算法在有向图中的复杂度为O(|V|Nmaxlg(Lmax)+|E|Nmax), 其中${{N}_{\max }}\text{=}{{2}^{k}}\left[ \frac{\Delta }{{{b}_{\min }}} \right]{{\left[ \frac{{{O}_{\max }}\Delta }{\varepsilon {{O}_{\min }}{{b}_{\min }}} \right]}^{\left[ 2 \right]}}$,但在无向图中每条边可能重复拓展,故实际复杂度应为O(|V|2Nmax2+|V|2Lmaxlg(Nmax))。 由于kVmax、Lmax远小于|V|、Nmax,因此KSRG相比这两类算法复杂度更优。
近似度分析 由于完全多项式时间近似策略,因此最终算法求得的解r′为ropt的近似解。设以KSRG方式实际求得的最优路径为re。由于完全多项式时间近似策略,关键词路径目标值与修正目标值之间满足OS′(τi,j)=θ-1OS(τi,j)」,因此满足如下式关系:
| $OS({{\tau }_{i,j}})-\theta \le \theta OS'({{\tau }_{i,j}})\le OS({{\tau }_{i,j}})$ | (3) |
令rd表示可行路径中有最小OS′(r)的路径,可得如下关系:
| $OS({{r}_{e}})\ge \theta \sum\limits_{\tau \subseteq {{r}_{e}}}{OS'({{\tau }_{i,j}})}=\theta OS'({{r}_{e}})\ge \theta OS'({{r}_{d}})$ | (4) |
对式(4) 最右部分进一步推导可得:
| $\begin{align} & \theta OS'({{r}_{d}})=\sum\limits_{\tau \subseteq {{r}_{d}}}{\theta OS'(\tau )}\ge \sum\limits_{\tau \subseteq {{r}_{d}}}{(OS(\tau )-\theta )}\ge \\ & \sum\limits_{\tau \subseteq {{r}_{d}}}{OS(\tau )}-\theta \left\lfloor \frac{\Delta }{\min \{BS({{\sigma }_{i,j}})\}} \right\rfloor \\ \end{align}$ |
由于$\theta =\frac{\varepsilon \min \{OS({{\tau }_{i,j}})\}\min \{BS({{\sigma }_{i,j}})\}}{\Delta }$,min{OS(τi,j)}≤OS(re),综合式(4) OS(rd)>OS(re)进一步可得OS(re)≥(1-ε)OS(rd),此外因为OS(rd)≥OS(r′),可得$OS(r')\le \frac{1}{1-\varepsilon }OS({{r}_{e}})$。由于re即为定理2中KSRopt,联立定理2最终得$OS(r')\le \frac{|\psi |}{1-\varepsilon }OS({{r}_{opt}})$。
4 实验与评估对提出的KSRG算法进行实验测试,并与OSScaling算法、BucketBound算法进行性能对比。所有算法均由Java语言编程实现,实验在PC上执行,处理器型号为AMD A8-7100 1.8 GHz,主存为4.0 GB,操作系统为Windows 8,JDK版本为1.7,Java虚拟机堆空间设定为512 MB。
4.1 实验数据集实验采用文献[20]提供的路网数据集,本文截取路网COL、NW、DE、ME中的部分点集与边集,通过程序去除其中的孤立点与冗余边构建连通子图G1、G2、G3、G4;结合文献[6]中的关键词数据集,为图中的顶点分配相应关键词构成本文数据集,具体如表 2所示。
| 表 2 实验图数据集 Table 2 Graph datasets for experiments |
本文随机使用范围在0到1间的小数对图中所有边的流行度权值进行赋值,流行度权值代表了某条边对应的路段热度,流行度权值越大表示该路段被游客访问的概率越高。
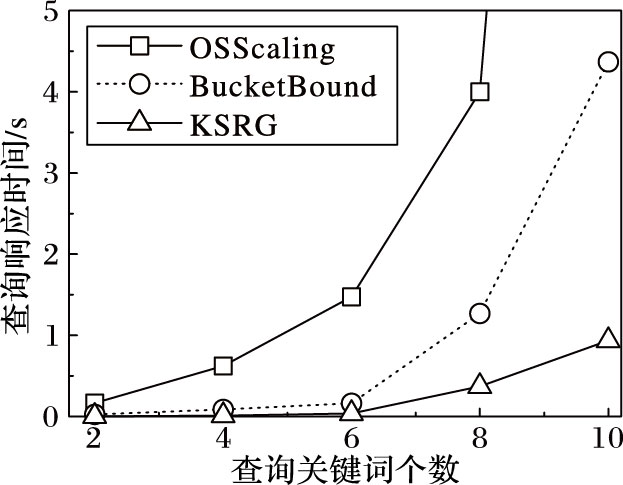
4.2 算法性能对比 4.2.1 不同查询关键词个数下运行结果为比较算法在不同查询关键词个数下的性能,在图G2中,随机选定两个顶点作为路径起点与终点,设定查询的代价约束为50 km,测试算法分别在关键词数目为2、4、6、8、10共五种情况下的查询性能,每种查询各运行5次,对运行时间取平均值,结果具体如图 2所示。
|
图 2 不同关键词个数下查询响应时间 Figure 2 Query response time with different number of keywords |
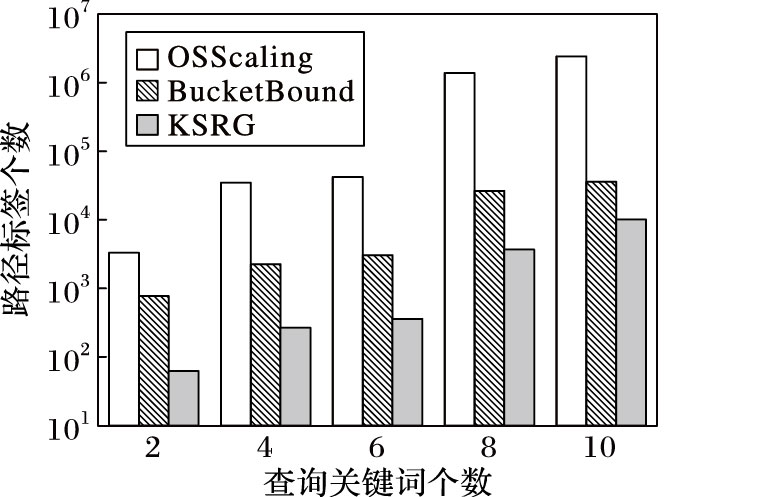
根据图 2,KSRG算法的查询响应时间远小于OSScaling以及BucketBound算法。OSScaling算法的查询响应时间最长,由于在查询关键词个数大于8时,运行时间大于10 s,因此不在图中标注。当查询关键词个数大于6时,OSScaling、BucketBound算法的响应时间显著增加,这是因为两者都采用邻边拓展的路径构建原则,将产生大量的路径标签;KSRG算法通过关键词路径拓展构建路径,仅考虑查询关键词相关的顶点,将产生更少路径标签,降低中间结果的处理代价因而响应时延更小。三类算法在查询过程中产生的路径标签的个数统计如图 3所示。根据图 3,OSScaling算法在查询中产生的路径标签数量约为KSRG算法的100倍,BucketBound算法产生的路径标签数量约为KSRG算法的10倍。大量路径标签的存储,使得OSScaling和BucketBound算法在多关键词查询过程中的空间开销过大,又由于查询过程中大量中间结果(路径标签)的处理操作,进而严重限制了查询效率。
|
图 3 不同查询关键词个数下路径标签产生数 Figure 3 Number of path labels generated with different number of queries |
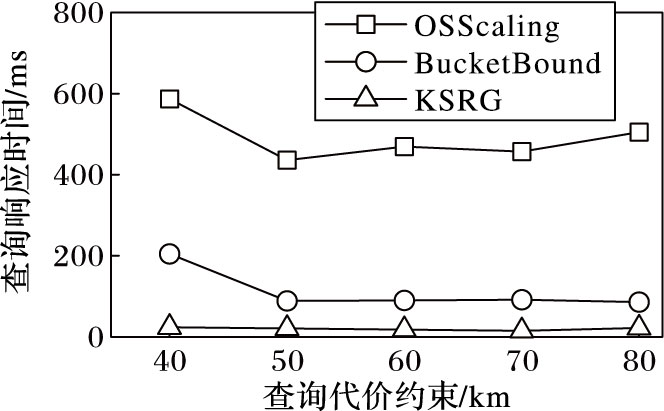
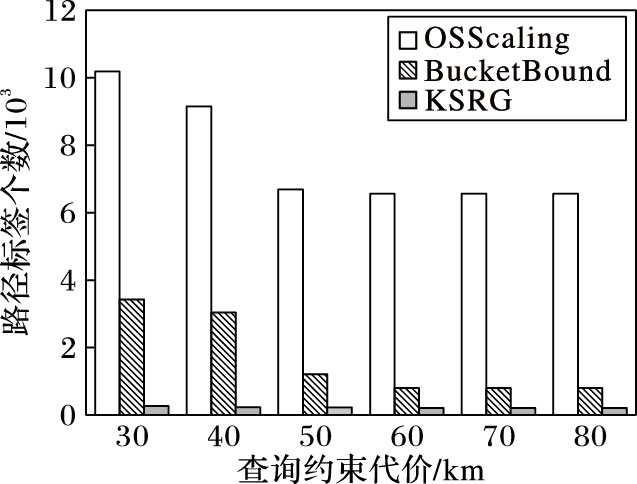
为比较不同代价约束对算法查询的影响,选定在图G4中进行查询测试。在图G4中同样随机选定两个顶点作为路径起点与终点,设定查询关键词个数为6,测试算法在代价约束为40、50、60、70、80 km共5类查询的运行情况,每类查询运行5次,对结果取平均值,如图 4所示。根据图 4,三类算法的查询响应时间随代价约束值的变大,呈现先减小后逐渐趋于稳定的趋势。这是因为,在一定范围内,较大的查询约束值能够使算法更早地求得可行路径标签,从而裁剪更多中间结果;当查询约束值继续增大时,由于最优解限定了目标值的上界,问题的解空间不再增大,故查询时间基本不变。三类算法在不同代价值约束下在查询过程中产生的路径标签数统计,如图 5所示。
|
图 4 不同查询代价约束下查询运行时间 Figure 4 Query running time with different cost constraints |
|
图 5 不同查询代价约束下路径标签产生个数 Figure 5 Number of path labels generated with different cost constraints |
综合图 4和图 5,在不同查询代价约束下,KSRG算法相比OSScaling算法及BucketBound算法,有更少的查询响应时间以及更小的空间开销代价。
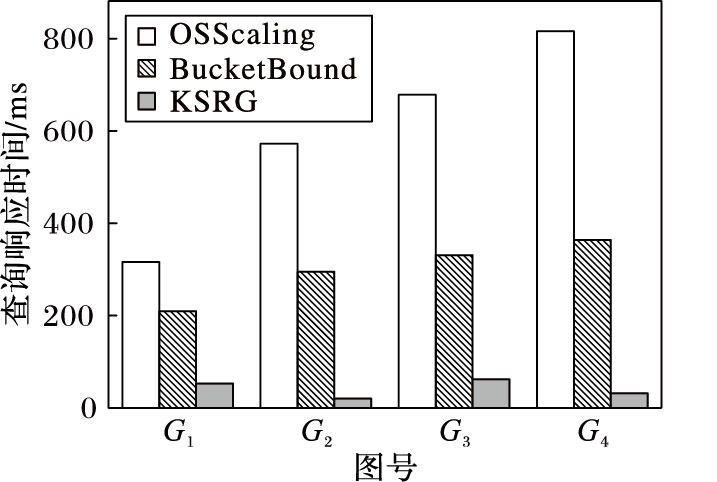
4.2.3 不同数据集下的运行结果为比较算法在不同数据集对应的图下的运行结果,在图G1、G2、G3、G4中随机选定两个顶点作为查询的起点与终点,统一设定查询关键词个数为6,代价约束为50 km,不同图下的查询各运行5次,对结果取平均,如图 6所示。根据图 6,OSScaling、BucketBound算法的查询响应时间随图尺寸变大呈线性增大趋势,因为随着图的变大,两种算法在邻边拓展过程中将遍历更多的顶点与边,产生更多的路径标签,增加查询处理代价。KSRG算法在不同尺寸图中运行时间呈现波动趋势,时间变化与图尺寸大小没有明显关联,因为KSRG算法通过关键词路径拓展产生关键词序列路径,该过程中对关键词顶点进行拓展,避免了无关顶点的遍历,故在代价约束确定后,查询代价不受图中顶点总数影响。
|
图 6 不同图中的查询响应时间 Figure 6 Query response time of different graphs |
考虑KSRG的路径拓展策略,影响查询响应性能的主要因素为查询关键词的频度和起点终点相对位置。
4.3.1 不同频度的查询关键词对查询的影响为比较关键词的频度对算法查询响应时间的影响,构建Q1、Q2、Q3和Q4共四类查询,每类查询都设定相同查询起点与终点,并统一查询代价约束为30 km,统一查询关键词个数为6。每类查询的关键词频度不同,具体如表 3所示。
| 表 3 查询中的关键词频度 Table 3 Keyword frequencies in queries |
在图G3中对上述四类查询进行测试,每类查询各运行5次,对查询响应时间取平均值,具体结果如表 4所示。
| 表 4 查询关键词频度对查询响应时间的影响 ms Table 4 Impact on response time caused by query keyword frequency ms |
根据表 3,KSRG算法对查询关键词的频度敏感。这是因为关键词频度越大,在每种关键词序列将枚举更多可行的关键词顶点序列,从而在查询过程产生更多路径标签。
4.3.2 查询起点与终点相对位置对响应时间的影响为比较查询中不同的起点与终点的相对位置对KSRG算法响应时间的影响,特构建四组查询Q5、Q6、Q7、Q8。每组查询设定代价约束为50 km;统一查询关键词个数为6;选择相距不同欧氏距离的起点与终点,具体如表 5所示。
| 表 5 查询点位置间欧氏距离 Table 5 Euclidean distance between query locations |
将上述四组查询在图G3中进行测试,结果如表 6所示。根据表 5,起点与终点间的欧氏距离越大,算法响应时间越长,这是因为在较大欧氏距离间隔下,两点间将包含更多关键词顶点,因此在查询过程也将产生更多的关键词序列路径对应的路径标签。
| 表 6 查询点间距离对查询响应时间的影响 ms Table 6 Impact on response time caused by distance between query locations ms |
为解决KORS在大图查询以及多关键词查询中复杂度过高、空间开销过大以及伸缩性较差的缺陷,本文提出了关键词序列路径构建算法——KSRG算法。该算法优先满足路径对查询关键词的全包含条件,采用关键词引导下的路径拓展提高可行路径的构建效率,从而减小路径构建过程中的空间开销;此外采用完全多项式时间近似策略,通过对路径目标值的倍率转换以及在查询过程中无效的路径标签过滤删除,进一步将问题求解的规模由阶乘级转化为多项式级。本文利用四组数据集对各类算法的查询性能作了综合对比,并分析影响查询效率的相关因素。实验表明,KSRG算法相比OSScaling和BucketBound算法在时间与空间开销以及可扩展性上有更优性能。
| [1] | RESNA R, LALLU A. Optimal route queries for road networks with user interest[J]. International Journal of Computer Trends and Technology, 2015, 21 (1) : 41-45. doi: 10.14445/22312803/IJCTT-V21P108 |
| [2] | CAO X, CHEN L, CONG G, et al. Keyword-aware optimal route search[J]. Proceedings of the VLDB Endowment, 2012, 5 (11) : 1136-1147. doi: 10.14778/2350229 |
| [3] | CONG G, CHEN L, CAO X, et al. KORS:keyword-aware optimal route search system[C]//ICDE'13:Proceedings of the 2013 IEEE International Conference on Data Engineering. Washington, DC:IEEE Computer Society, 2013:1340-1343. |
| [4] | CONG G, JENSEN C S. Querying geo-textual data:spatial keyword queries and beyond[C]//SIGMOD'16:Proceedings of the 2016 International Conference on Management of Data. New York:ACM, 2016:2207-2212. |
| [5] | CONG G, JENSEN C S, WU D. Efficient retrieval of the top-k most relevant spatial Web objects[J]. Proceedings of the VLDB Endowment, 2009, 2 (1) : 337-348. doi: 10.14778/1687627 |
| [6] | CAO X, CONG G, JENSEN C S, et al. Collective spatial keyword querying[C]//SIGMOD'11:Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data. New York:ACM, 2011:373-384. |
| [7] | CHEN L, CONG G, JENSEN C S, et al. Spatial keyword query processing:an experimental evaluation[J]. Proceedings of the VLDB Endowment, 2013, 6 (3) : 217-228. doi: 10.14778/2535569 |
| [8] | CHOUDHURY F M, CULPEPPER J S, SELLIS T, et al. Maximizing bichromatic reverse spatial and textual k nearest neighbor queries[J]. Proceedings of the VLDB Endowment, 2016, 9 (6) : 456-467. doi: 10.14778/2904121 |
| [9] | CAO X, CONG G, JENSEN C S, et al. Retrieving regions of interest for user exploration[J]. Proceedings of the VLDB Endowment, 2014, 7 (9) : 733-744. doi: 10.14778/2732939 |
| [10] | LI F F, CHENG D, HADJIELEFTHERIOU M, et al. On trip planning queries in spatial databases[C]//Proceedings of the 9th International Symposium on Advances in Spatial and Temporal Databases, LNCS 3633. Berlin:Springer-Verlag, 2005:273-290. |
| [11] | SHARIFZADEH M, KOLAHDOUZAN M, SHAHABI C. The optimal sequenced route query[J]. The VLDB Journal, 2008, 17 (4) : 765-787. doi: 10.1007/s00778-006-0038-6 |
| [12] | CHEN H, KU W-S, SUN M-T, et al. The multi-rule partial sequenced route query[C]//GIS'08:Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2008:Article No. 10. |
| [13] | LI J, YANG Y, MAMOULIS N. Optimal route queries with arbitrary order constraints[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25 (5) : 1097-1110. doi: 10.1109/TKDE.2012.36 |
| [14] | 宋晓宇, 许鸿斐, 孙焕良, 等. 基于签到数据的短时间体验式路线搜索[J]. 计算机学报, 2013, 36 (8) : 1693-1703. ( SONG X Y, XU H F, SUN H L, et al. Short-term experience route search based on check-in data[J]. Chinese Journal of Computers, 2013, 36 (8) : 1693-1703. ) |
| [15] | 鲍金玲, 杨晓春, 王斌, 等. 一种支持约束关系的高效的行程规划算法[J]. 小型微型计算机系统, 2013, 34 (12) : 2702-2707. ( BAO J L, YANG X C, WANG B, et al. An efficient trip planning algorithm under constraint[J]. Journal of Chinese Computer Systems, 2013, 34 (12) : 2702-2707. ) |
| [16] | CHEN Z, SHEN H T, ZHOU X. Discovering popular routes from trajectories[C]//ICDE'11:Proceedings of the 2011 IEEE 27th International Conference on Data Engineering. Washington, DC:IEEE Computer Society, 2011:900-911. |
| [17] | FLOYD R W. Algorithm 97:shortest path[J]. Communications of the ACM, 1962, 5 (6) : 345. |
| [18] | CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to algorithms[M]. 3rd ed. Cambridge, MA: MIT Press, 2009 : 450 -462. |
| [19] | DUMITRESCU I, BOLAND N. Improved preprocessing, labeling and scaling algorithms for the weight-constrained shortest path problem[J]. Networks, 2003, 42 (3) : 135-153. doi: 10.1002/(ISSN)1097-0037 |
| [20] | ABEYWICKRAMA T, CHEEMA M A, TANIAR D. K-nearest neighbors on road networks:a journey in experimentation and in-memory implementation[J]. Proceedings of the VLDB Endowment, 2016, 9 (6) : 492-503. doi: 10.14778/2904121 |




