2. 桂林理工大学 测绘地理信息学院, 广西 桂林 541004
2. College of Geomatics and Geoinformation, Guilin University of Technology, Guilin Guangxi 541004, China
近20年来,元启发式算法得到了迅速发展。它源自于自然现象的启发,在解决复杂计算问题时提供了一种新的手段,典型的有遗传算法(Genetic Algorithm, GA)[1]、粒子群(Particle Swarm Optimization, PSO)算法[2]、差分进化(Differential Evolution, DE)算法[3]、引力搜索算法(Gravitational Search Algorithm, GSA)[4]等。
2014年,学者Mirjalili等[5]提出了一种新型的元启发式算法——灰狼优化(Grey Wolf Optimizer, GWO)算法。它是一种模拟自然界灰狼群体狩猎行为的智能优化算法,以其快速收敛性、参数较少和编程易实现等优点而备受关注。GWO算法已经成功应用于传感器网络训练[6]、直流电机最优控制[7]、经济调度指派[8]、表面波参数优化[9]等领域。尽管GWO算法得到了广泛的应用,但是基本GWO算法和其他优化算法一样,面临着易收敛于局部最优的缺陷。为此,许多研究人员展开了深入研究,并提出了一些改进策略,如Nasrabadi等[10]提出采用反向学习策略来增加种群多样性,同时为了实现算法深度寻优,对算法进行并行化处理,但该改进策略加重了计算机运行负担;龙文等[11]提出混沌和精英反向学习的混合策略来改进GWO算法,在高维优化问题上取得了较好效果,拓宽了GWO算法的应用范围;Zhu等[12]构建了一种DE和GWO相混合的混合GWO(Hybrid GWO, HGWO)算法,但由于采取的是两种优化算法之间的相互混合,改进后的算法体系过于庞大且寻优精度也不太理想;魏政磊等[13]提出利用位置矢量差来跳出局部最优,但由于算法迭代后期灰狼之间的位置矢量差很小,对灰狼位置的扰动能力一般。
基于以上研究者对GWO算法的改进研究经验可知, 找到一种简单且高效的改进策略十分必要。本文考虑到算法位置更新向量中前三头狼的不同特征,提出引入权值因子来动态调整算法的位置向量更新方程;同时为了摆脱局部最优,提出采用概率扰动策略来增强算法迭代后期的种群多样性。通过对18个基准测试函数的仿真实验,与4种优化算法作比较,实验结果验证了所提改进GWO(Improved GWO, IGWO)是有效的,从而为GWO算法的改进提供了一种新的思路。
1 基本灰狼优化算法灰狼是位于食物链顶端的食肉型动物,多以群居为主,并构建了严格的金字塔式社会等级制度,如图 1所示。图 1中,等级最高的狼为α,其他依次为β、δ和ω。α是整个狼群的领导者,负责主要事务的决策;β是α的接替者,协助α的管理;δ服从α和β的领导,负责侦查和守卫整个狼群的安全;ω位于金字塔最底狼,完成高层狼交代的任务。
|
图 1 灰狼金字塔等级 Figure 1 Hierarchic pyramid of grey wolf population |
对应于GWO算法函数优化问题时,适应度最高的个体被赋予α,两个次优个体分别定义为β和δ,剩余的其他个体为ω。灰狼群体狩猎时,由α带领,β和δ协助,其余ω听从指挥,主要进行包围、猎捕和攻击三个步骤[14],最终高成功率地捕获猎物(全局最优解)。
首先,灰狼群对猎物进行包围,该过程的数学描述为:
| $ \mathit{\boldsymbol{D}} = \left| {\mathit{\boldsymbol{C}} \cdot {\mathit{\boldsymbol{X}}_p}(t)-\mathit{\boldsymbol{X}}(t)} \right| $ | (1) |
| $\mathit{\boldsymbol{X}}(t + 1) = {\mathit{\boldsymbol{X}}_p}(t) - \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{D}}$ | (2) |
| $ \mathit{\boldsymbol{A}} = 2a \cdot {\mathit{\boldsymbol{r}}_1}-a $ | (3) |
| $\mathit{\boldsymbol{C}} = 2{\mathit{\boldsymbol{r}}_2}$ | (4) |
其中:Xp表示猎物的位置;X(t)表示第t代时灰狼个体的位置;A和C为系数向量;r1和r2为[0, 1]之间取值的随机向量;a为控制参数。
其次,灰狼群进行猎捕。该过程由α、β和δ狼来引导,更新灰狼个体位置,数学描述如下:
| $ {\mathit{\boldsymbol{D}}_\alpha } = \left| {{\mathit{\boldsymbol{C}}_1} \cdot {\mathit{\boldsymbol{X}}_\alpha }-\mathit{\boldsymbol{X}}(t)} \right| $ | (5) |
| $ {\mathit{\boldsymbol{D}}_\beta } = \left| {{\mathit{\boldsymbol{C}}_2} \cdot {\mathit{\boldsymbol{X}}_\beta }-\mathit{\boldsymbol{X}}(t)} \right| $ | (6) |
| $ {\mathit{\boldsymbol{D}}_\delta } = \left| {{\mathit{\boldsymbol{C}}_3} \cdot {\mathit{\boldsymbol{X}}_\delta }-\mathit{\boldsymbol{X}}(t)} \right| $ | (7) |
| $ {\mathit{\boldsymbol{X}}_1} = {\mathit{\boldsymbol{X}}_\alpha }-{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{D}}_\alpha } $ | (8) |
| $ {\mathit{\boldsymbol{X}}_2} = {\mathit{\boldsymbol{X}}_\beta }-{\mathit{\boldsymbol{A}}_2} \cdot {\mathit{\boldsymbol{D}}_\beta } $ | (9) |
| $ {\mathit{\boldsymbol{X}}_3} = {\mathit{\boldsymbol{X}}_\delta }-{\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{D}}_\delta } $ | (10) |
| $ \mathit{\boldsymbol{X}}(t + 1) = \left( {{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{X}}_2} + {\mathit{\boldsymbol{X}}_3}} \right)/3 $ | (11) |
最后,灰狼群进行攻击,完成捕获猎物这一目标。攻击行为主要依据式(3)中的a值随迭代次数由2线性递减到0来实现。当|A|≤1时,灰狼群对猎物集中攻击,对应于局部搜索;当|A|>1灰狼散去,进行全局搜索。
2 改进灰狼优化算法 2.1 引入权值因子基本GWO算法通过计算三个最佳灰狼位置的平均值来更新灰狼位置,这种策略并没有考虑三头狼在群体狩猎活动中的贡献度问题。由于GWO算法的狼α并不一定是全局最优解,这时在不断迭代中,随着其余狼ω向这三头狼逼近,这就容易陷入局部最优[15]。本文从最佳灰狼贡献问题角度设计一种权重因子,用来提升GWO算法的寻优能力。由于GWO算法中的系数向量A和C是动态随机的,而权重因子也应该随着寻优过程非线性调整变化,为此本文设计的权重因子来源于系数向量A和C。在基本GWO算法中,A1、A2、A3以及C1、C2、C3是不相同的,在这里为了保证权重因子更新的相关联性,设计A1、A2和A3相同,C1、C2和C3相同,如下:
| $ {\mathit{\boldsymbol{A}}_1} = {\mathit{\boldsymbol{A}}_2} = {\mathit{\boldsymbol{A}}_3} = 2a \cdot {\mathit{\boldsymbol{r}}_1}-a $ | (12) |
| $ {\mathit{\boldsymbol{C}}_1} = {\mathit{\boldsymbol{C}}_2} = {\mathit{\boldsymbol{C}}_3} = 2{\mathit{\boldsymbol{r}}_2} $ | (13) |
那么,设计的位置向量权重因子分别为:
| $ {w_1} = \frac{{\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}}{{\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right| + \left| {{\mathit{\boldsymbol{A}}_2} \cdot {\mathit{\boldsymbol{C}}_2}} \right| + \left| {{\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{C}}_3}} \right|}} = \frac{1}{3} $ | (14) |
| $ {w_2} = \frac{{\left| {{\mathit{\boldsymbol{A}}_2} \cdot {\mathit{\boldsymbol{C}}_2}} \right|}}{{{w_1} + \left| {{\mathit{\boldsymbol{A}}_2} \cdot {\mathit{\boldsymbol{C}}_2}} \right| + \left| {{\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{C}}_3}} \right|}} = \frac{{3\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}}{{1 + 6\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}} $ | (15) |
| $ \begin{array}{l} {w_3} = \frac{{\left| {{\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{C}}_3}} \right|}}{{{w_1} + {w_2} + \left| {{\mathit{\boldsymbol{A}}_3} \cdot {\mathit{\boldsymbol{C}}_3}} \right|}} = \\ \;\;\;\;\;\frac{{18{{\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}^2} + 3\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}}{{18{{\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right|}^2} + 18\left| {{\mathit{\boldsymbol{A}}_1} \cdot {\mathit{\boldsymbol{C}}_1}} \right| + 1}} \\ \end{array} $ | (16) |
因此,得到新的位置更新公式为:
| $ \mathit{\boldsymbol{X}}(t + 1) = \frac{{{w_1}{\mathit{\boldsymbol{X}}_1} + {w_2}{\mathit{\boldsymbol{X}}_2} + {w_3}{\mathit{\boldsymbol{X}}_3}}}{3} $ | (17) |
随着GWO算法迭代次数的不断增加,算法寻优逐渐趋于收敛,一旦收敛于局部最优很难跳出。在算法种群更新中加入扰动机制可以有效提升算法跳出局部最优的能力[16]。本文设计带有一定概率的扰动来增强算法寻优后期的种群多样性,为摆脱局部收敛创造有利条件。对于概率扰动策略,在以往的一些优化算法中有所研究,如胡宏梅等[17]提出采用随机概率扰动方式作为基本粒子群算法的全局更新条件,从而增强全局寻优区域的搜索能力,但它采用的是模拟退火算法的退火概率,计算过于复杂;张伟[18]提出在差分进化算法中运用小概率扰动操作来增强种群的多样性,但它采用固定的概率形式,无法在不同迭代过程中充分发挥扰动策略。为此,本文设计一种简便且高效的扰动概率公式为:
| $P = \frac{{(G - 1){{\rm{e}}^{(t - 1)/T}}}}{{4G}}$ | (18) |
其中:P为扰动概率;G为优化问题的维度;T为最大迭代次数。算法迭代初期,扰动概率较小,以便算法快速寻找全局最优解;算法迭代后期,扰动概率增加,增强了种群多样性。一般来说T是一个较大的常数,当算法迭代至后期t→T,扰动概率
| $\mathit{\boldsymbol{M}}(t + 1) = \mathit{\boldsymbol{lb}} + {\mathit{\boldsymbol{r}}_3} \cdot (\mathit{\boldsymbol{ub}} - \mathit{\boldsymbol{lb}});\;{\mathit{\boldsymbol{r}}_3} < P$ | (19) |
其中:M为扰动后的个体;lb为灰狼个体位置的下界;ub为灰狼个体位置的上界;r3为[0, 1]之间取值的随机向量。扰动后的灰狼个体基于贪婪机制进行更新,更新公式为:
| $ \mathit{\boldsymbol{X}}(t + 1) = \left\{ \begin{array}{l} \mathit{\boldsymbol{M}}(t + 1), \;\;\;f(\mathit{\boldsymbol{M}}(t + 1)) < f(\mathit{\boldsymbol{X}}(t + 1))\\ \mathit{\boldsymbol{X}}(t + 1), \;\;\;\;其他 \end{array} \right.$ | (20) |
其中:f(M(t+1))和f(X(t+1))分别表示第t+1代扰动个体M和灰狼个体X的目标函数值。
采用非线性收敛因子和概率扰动混合策略改进的GWO算法的伪代码,见算法1。
算法1 采用动态权重和概率扰动改进的灰狼优化算法。
Initialize iteration count (T)
Initialize size of the pack (N)
Initialize the grey wolf population Xi(i=1, 2, …, N)
Initialize a, A and C
Calculate the fitness of each grey wolf
Xα = the best grey wolf
Xβ = the second best grey wolf
Xδ = the third best grey wolf
while t≤T do
for t = 1 to N
Calculate the disturbance probability P
if rand()≥P
Calculate weights for α, β and δ and by equation (14)~(16)
Update position vector by equation (17)
else
Generate random individual M by equation (19)
Update position vector by equation (20)
end if
end for
Update a, A and C
Calculate the fitness of each grey wolf
Update Xα, Xβ and Xδ
end while
3 数值分析与实验结果 3.1 测试函数和实验设置为了验证IGWO算法的寻优性能,对18个基准测试函数进行测试,同时选取传统的优化算法DE算法、GSA以及新型优化算法GWO算法、文献[12]提出的HGWO算法进行比较。这18个基准测试函数分为三类:第一类为单峰基准测试函数F1~F6,如表 1所示;第二类为多峰基准测试函数F7~F12,如表 2所示;第三类为固定维度多峰基准测试函数F13~F18,如表 3所示。为保证各算法公平以及达到收敛状态,所有算法的种群规模设置为30,最大迭代次数设置为500。其中为了便于比较各算法,依照参考文献[4],GSA的常数α取20,G0取100;依照参考文献[12],DE算法的缩放因子F取0.5,交叉概率因子Pc取0.2。
| 表 1 单峰基准测试函数 Table 1 Unimodal benchmark test functions |
| 表 2 多峰基准测试函数 Table 2 Multimodal benchmark test functions |
| 表 3 固定维度多峰基准测试函数 Table 3 Multimodal benchmark test functions with fixed-dimension |
为了减少随机性对结果的影响,各算法独立运行30次,以30次结果平均值测试算法的搜索精度;30次结果的标准差测试算法的稳定性。IGWO、HGWO、GWO、GSA和DE算法对18个基准测试函数的测试结果,如表 4~6所示。
| 表 4 单峰基准测试函数测试结果 Table 4 Test results of unimodal benchmark test functions |
| 表 5 多峰基准测试函数测试结果 Table 5 Test results of multimodal benchmark test functions |
| 表 6 固定维度多峰基准测试函数测试结果 Table 6 Test results of multimodal benchmark test functions with fixed-dimension |
从表 4~6中可以看出,IGWO算法相对于HGWO算法,除函数F11、F12和F14~F18外,IGWO算法的搜索精度均优于HGWO算法,且搜索结果十分稳定;相对于算法GWO和GSA,除函数F15~F18外,无论搜索精度还是算法稳定性上,均体现出了明显优势;相对于DE算法,IGWO算法除对函数F12和F15~F18的寻优结果略逊色外,对于其他函数的搜索精度明显好于DE算法,且算法稳定性更好。综上,IGWO算法除对固定维度多峰基准函数寻优略逊色外,对于其他函数,IGWO算法的搜索精度更高,表现出良好的算法稳定性。
为了进一步说明IGWO算法的优越性,5种算法对不同函数的收敛曲线如图 2所示。考虑到篇幅限制,本文示例性列出了典型的6种基准测试函数的收敛曲线,具体为:单峰基准测试函数F1和F2,多峰基准测试函数F7和F8,固定维度多峰基准测试函数F13和F14。
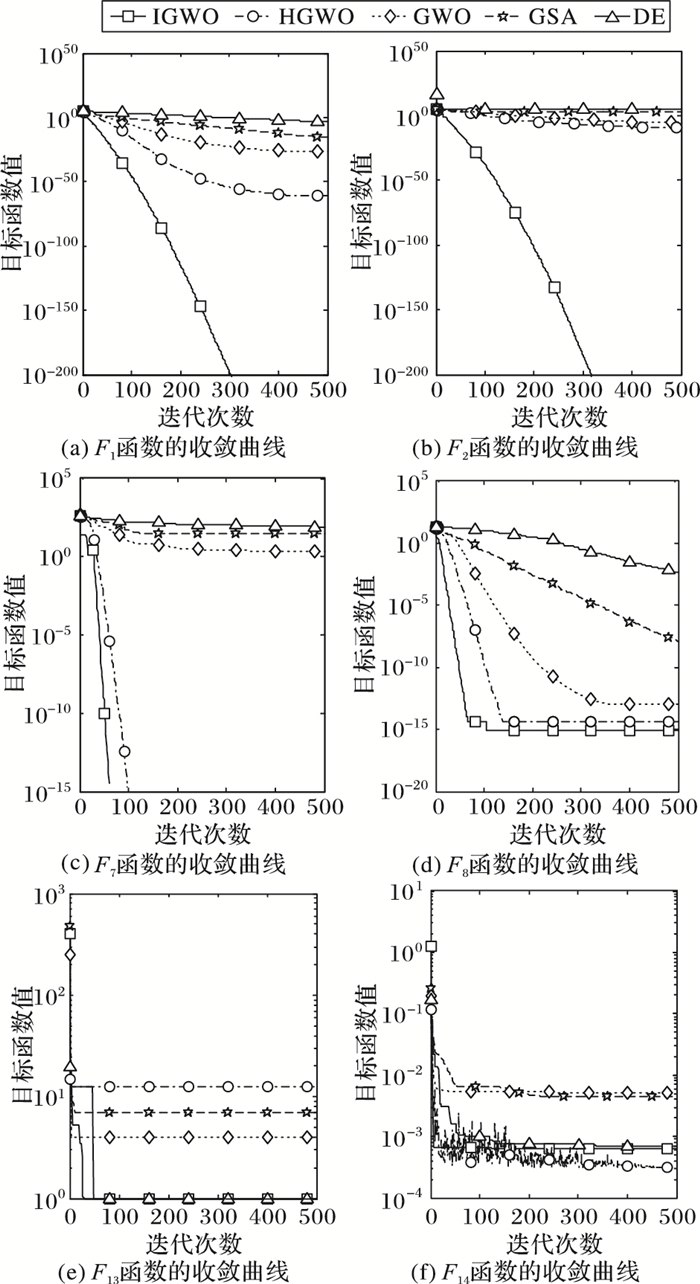
|
图 2 不同算法对不同基准测试函数的目标函数值曲线 Figure 2 Objective function value curves of different algorithms for different benchmark test functions |
从图 2中可以看出,不论单峰基准测试函数、多峰基准测试函数还是固定维度多峰基准测试函数,相对于HGWO、GWO、GSA和DE算法,IGWO算法具有更快的收敛速度,达到了更高的搜索精度。总的来说,IGWO算法的搜索性能优于另外4种寻优算法。
实验中对IGWO算法的代码进行分析知,IGWO算法的时间复杂度为O(TN),相比基本GWO算法,它的时间复杂度并没有改变,说明IGWO算法的计算效率依旧保持着较高水平。
4 结语针对基本灰狼优化算法中位置向量更新方程的不合理性,本文提出引入动态的权值因子来调整算法的位置向量;针对算法易陷入局部最优的问题,本文提出采用概率扰动策略增强算法迭代后期的种群多样性。通过对18个基准测试函数的仿真实验,结果表明,与基本灰狼优化算法、混合灰狼优化算法、引力搜索算法和差分进化算法相比,本文提出的改进算法具有更高的搜索性能,克服了GWO算法在多峰基准测试函数优化中易陷入局部最优的缺点。此外,如何利用改进的灰狼优化算法解决支持向量机和神经网络参数优化问题是下一步需要研究的方向。
| [1] | TANG K S, MAN K F, KWONG S, et al. Genetic algorithms and their applications[J]. IEEE Signal Processing Magazine, 1996, 13(6): 22-37. DOI:10.1109/79.543973 |
| [2] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ:IEEE, 1995:1942-1948. |
| [3] | STORN R, PRICE K. Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [4] | RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA:a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248. DOI:10.1016/j.ins.2009.03.004 |
| [5] | MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61. |
| [6] | MIRJALILI S. How effective is the grey wolf optimizer in training multi-layer perceptrons[J]. Applied Intelligence, 2015, 43(1): 150-161. DOI:10.1007/s10489-014-0645-7 |
| [7] | MADADI A, MOTLAGH M. Optimal control of DC motor using grey wolf optimizer algorithm[J]. Technical Journal of Engineering and Applied Sciences, 2014, 4(4): 373-379. |
| [8] | SONG H M, SULAIMAN M H, MOHAMED M R. An application of grey wolf optimizer for solving combined economic emission dispatch problems[J]. International Review on Modelling and Simulations, 2014, 7(5): 838-844. DOI:10.15866/iremos.v7i5.2799 |
| [9] | SONG X H, TANG L, ZHAO S T, et al. Grey wolf optimizer for parameter estimation in surface waves[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 147-157. DOI:10.1016/j.soildyn.2015.04.004 |
| [10] | NASRABADI M S, SHARAFI Y, TAYARI M. A parallel grey wolf optimizer combined with opposition based learning[C]//Proceedings of the 20161st Conference on Swarm Intelligence and Evolutionary Computation. Piscataway, NJ:IEEE, 2016:18-23. http://ieeexplore.ieee.org/document/7482116/ |
| [11] | 龙文, 蔡绍洪, 焦建军, 等. 求解高维优化问题的混合灰狼优化算法[J]. 控制与决策, 2016, 31(11): 1991-1997. (LONG W, CAI S H, JIAO J J, et al. Hybrid grey wolf optimization algorithm for high-dimensional optimization[J]. Control and Decision, 2016, 31(11): 1991-1997.) |
| [12] | ZHU A J, XU C P, LI Z, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317-328. DOI:10.1109/JSEE.2015.00037 |
| [13] | 魏政磊, 赵辉, 韩邦杰, 等. 具有自适应搜索策略的灰狼优化算法[J]. 计算机科学, 2017, 44(3): 259-263. (WEI Z L, ZHAO H, HAN B J, et al. Grey wolf optimization algorithm with self-adaptive searching strategy[J]. Computer Science, 2017, 44(3): 259-263. DOI:10.11896/j.issn.1002-137X.2017.03.053) |
| [14] | MITTAL N, SINGH U, SOHI B S. Modified grey wolf optimizer for global engineering optimization[J]. Applied Computational Intelligence and Soft Computing, 2016, 2016: Article ID 7950348. |
| [15] | 郭振洲, 刘然, 拱长青, 等. 基于改进灰狼算法的RBF神经网络研究[J]. 微电子学与计算机, 2017, 34(7): 7-10. (GUO Z Z, LIU R, GONG C Q, et al. Study on RBF neural network based on gray wolf optimization algorithm[J]. Microelectronics & Computer, 2017, 34(7): 7-10.) |
| [16] | 徐辰华, 李成县, 喻昕, 等. 基于Cat混沌与高斯变异的改进灰狼优化算法[J]. 计算机工程与应用, 2017, 53(4): 1-9. (XU C H, LI C X, YU X, et al. Improved grey wolf optimization algorithm based on chaotic cat mapping and Gaussian mutation[J]. Computer Engineering and Applications, 2017, 53(4): 1-9.) |
| [17] | 胡宏梅, 董恩清. 基于粒子群算法的码书设计研究[J]. 微电子学与计算机, 2009, 26(1): 97-100. (HU H M, DONG E Q. Study of codebook design based on particle swarm optimization[J]. Microelectronics and Computer, 2009, 26(1): 97-100.) |
| [18] | 张伟. 差分进化算法的改进研究[D]. 西安: 西安电子科技大学, 2014: 13-15. (ZHANG W. Improved research of differential evolution algorithm[D]. Xi'an:Xidian University, 2014:13-15.) http://cdmd.cnki.com.cn/Article/CDMD-10701-1015433524.htm |




