2. 河南省高等学校控制工程重点学科开放实验室, 河南 焦作 454000
2. Key Laboratory of Control Engineering of Henan Province, Jiaozuo Henan 454000, China
数字多媒体处理技术和网络技术的发展,使得数字媒体的复制、编辑处理和分布更加容易和便捷,图像是人们接触最多的多媒体,而且也是包含信息面最广的网络多媒体,它涉及到生活的方方面面,近年来发生的图像非法合成、复制、篡改事件,侵害了所有人的合法权益。有效判定图像版权归属是图像拷贝检测研究的热点和难点之一。
如何提取鲁棒性强、处理速度快、占用内存少的图像特征是拷贝检测方法的关键问题。根据图像特征提取的方法可分为两类:基于图像全局特征的方法和基于图像局部特征的方法。利用图像的亮度均值、顺序测度[1]、离散余弦变换(Discrete Cosine Transform, DCT)系数、非负矩阵分解(Non-negative Matrix Factorization, NMF)和直方图[2]统计信息等构造图像特征的算法属于第一类方法。邹复好等[3]提出基于圆环分区的顺序测度算法,以图像中心为圆心,依据图像的尺寸构建一个最大的内切圆形区域,然后将该圆形区域划分为多个圆环,并计算各圆环特征的顺序测度作为图像特征向量。与Kim[4]采用DCT系数中直流系数的方法相比,邹复好等[3]的算法在抗旋转和裁剪失真方面有着良好的性能,可抵抗任意角度的旋转和一定幅度的裁剪;但是对平移、局部裁剪、拉伸、和旋转缩放裁剪的混合攻击等失真抵抗能力一般。Monga等[5]提出NMF方法,该方法将矩阵分解为非负子矩阵,使非负系数描述图像局部的能力增强,该方法对噪声、压缩、模糊的鲁棒性非常好,但是存在对Gamma校正和几何攻击的鲁棒性较弱的问题。
利用图像特征点的方法属于第二类方法,特征点就是指一些能够稳定出现并且具有较好的可区分性的一些点。例如在图像不完全受到遮挡的情况下,一些特征依然稳定存在,以代表这幅图像。鉴于此,局部特征被越来越广泛地应用于图像检索、目标检测与跟踪、图像匹配等领域,比如Harris兴趣点[6]、SIFT特征点[7]、主成分分析-尺度不变特征变换(Principle Component Analysis-Scale Invariant Feature Transform, PCA-SIFT)特征[8]。SIFT是由Lowe[9]于2004年提出的,该特征描述子是通过对特征点邻域构建三维梯度方向直方图来产生128维特征向量。SIFT特征对旋转和尺度变换具有不变性,对仿射变换和噪声也保持一定的稳定性,在匹配中具有较好的容错性;但SIFT特征维数较高,存在匹配效率不高的问题。针对局部特征描述向量维数较高的问题,Ke等[10]最早采用PCA进行局部特征描述降维,该方法将特征点邻域像素的梯度分量所构成高维向量投影到前20维本征向量空间,产生20维的特征描述。PCA-SIFT方法虽然可以产生紧凑的低维数特征描述向量,但是它的算法复杂度较高,计算过程十分耗时。针对这一问题,颜雪军等[11]提出采用二维PCA(Two-dimensional PCA, 2DPCA)方法对梯度向量描述块进行降维来构建特征描述子,实验结果表明,该方法相比PCA-SIFT,可以快速地求解本征空间,并且从计算效率上看,2DPCA-SIFT具有更好的扩展性。Lyu等[12]将Harris和SIFT检测联合起来并结合特征点的分布提出了一种形状上下文指纹(Radial and Angular Shape Context Hashing, R&ASCH)算法,该算法对常规信号处理的鲁棒性有了大幅提高,尤其是几何攻击方面。针对SIFT算法匹配速度慢的问题,许佳佳等[13]提出了一种改进的Harris-SIFT算法,对传统Harris算法进行改进,然后利用SIFT算子的特征描述方法对提取的特征点进行描述,通过随机kd树算法对两幅图像的特征点进行匹配,大大减少了标准SIFT所需的配准时间。Ling等[14]也以SIFT特征点为基础,采用其生成一系列32比特二值序列的词库,并且构建了一个查找表用于大规模图像检索。基于特征点构造特征的缺点在于计算复杂、有较低的检测效率,优点是对几何攻击稳定。
综上所述,当前以SIFT的描述子为基础的图像拷贝算法,构建哈希序列时每一幅图像提取若干个特征点,每个特征点对应一个哈希序列,即每幅图像对应若干个哈希序列,SIFT特征描述子计算耗时,即使采用PCA进行局部特征描述降维,也存在特征提取时间耗时长与匹配效率不高的问题,受此启发,本文以保证检测精度和提高特征提取速度、匹配速度为目标,避开128维SIFT描述子计算,利用SIFT特征点的2维位置分布及1维方向分布特征,构建级联式过滤框架,实现拷贝检测。本文算法在保持高检测精度的同时,显著提高特征提取速度和匹配速度,满足在线拷贝检测的需求。
1 SIFT算子点特征是图像最基本的局部特征之一,具有普遍性、容易表示等优点[15]。选择SIFT算子主要理由是SIFT特征是图像局部区域梯度突出关系的一种反映,不但对旋转、尺度缩放具有不变性,同时对亮度变化、噪声、滤波、仿射变换、视角变换等也有较好的鲁棒性,并且对每幅图像生成的特征点数量非常多,这些因素使得图像中特征点保持数量和位置分布的稳定性,是目前公认的最为稳定的特征匹配算子[16]。
2 特征提取算法描述完整的图像拷贝检测系统框架包括特征数据库生成和拷贝检测两个阶段,其中特征数据库包括测试特征库和原始图像特征库,拷贝检测阶段采用两级过滤式检测。具体流程如图 1所示。
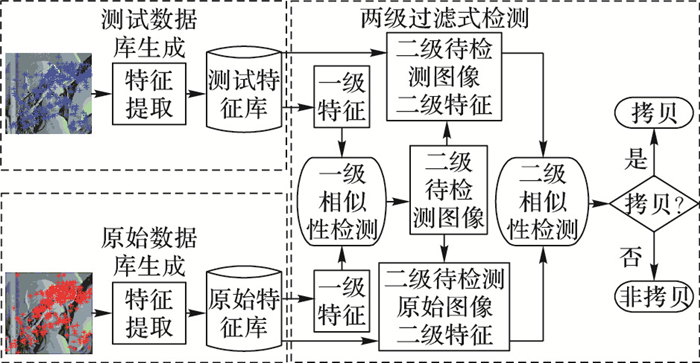
|
图 1 图像拷贝检测系统流程 Figure 1 Flow chart of image copy detection system |
图像的一级鲁棒特征是基于图像的SIFT特征点位置信息与中心点得到的参数,具体生成过程如下:
对于一幅大小为M×M的图像,假设提取得到的SIFT特征点数量为Z,其中一个SIFT特征点坐标T=(xt, yt),图像中心点坐标R=(r, r)(r=M/2)。
特征点T与中心点R的距离可表示为:
| $ {d_t} = \sqrt {{{\left({{x_t}-r} \right)}^2} + {{\left({{y_t}-r} \right)}^2}} $ | (1) |
向量角度表示为:
| $ {{\alpha }_{t}}=\text{arctan}\left( \left( {{y}_{t}}-r \right)/\left( {{x}_{t}}-r \right) \right) $ | (2) |
统计图像中所有的SIFT特征点与中心点R的距离、角度分别为:
| $ \mathit{\boldsymbol{D}} = \left[{{d_1}, {d_2}, \cdots, {d_t}, \cdots, {d_z}} \right] $ | (3) |
| $ \mathit{\boldsymbol{\theta}} = \left[{{\alpha _1}, {\alpha _2}, \cdots, {\alpha _t}, \cdots, {\alpha _z}} \right] $ | (4) |
采用数量分类统计的方法构造哈希,根据角度θ的分布范围[-π, π],将角度均匀划分为p份,生成p维列向量M=[m1; m2; …; mi; mi+1; …; mp],其中mi表示落在第i个角度区间的SIFT特征点数量。
同时,在角度划分成p份的基础上,将图像基于圆环等面积划分为q份,假设在第i个角度区间上,可对应生成1维行向量N=[di1, di2, …, dij, dij+1, …, diq],由此可生成矩阵:
| $ \mathit{\boldsymbol{V}} = \left({V\left({i, j} \right)} \right) $ | (5) |
其中V(i, j)(i=1, 2, …,p; j=1, 2, …,q)坐标表示落在第i个角度区间第j个距离区间的SIFT特征点数量。
将V(i, j)在所有角度、距离上形成一维向量,并通过与均值比较生成一维二值哈希序列:
| $\mathit{\boldsymbol{H}} = \left[{{h_1}, {h_2}, \cdots, {h_k}, {h_{k + 1}}, \cdots, {h_{p \times q}}} \right]$ | (6) |
其中
图像的二级鲁棒特征是基于图像的SIFT特征点方向信息得到的参数,根据特征点的方向分布范围[-π, π],基本符合均匀分布规律,因此将方向区间均匀划分为l份,第m个区间内的方向数量表示为ωm,对应的向量Ω=[ω1, ω2, …, ωm, ωm+1, …, ωl]。
2.3 级联检索根据图 1,在两级过滤式检测阶段,首先进行一级特征相似性检测,假设原始特征库中图像一级特征为V′,采用“顺序扫描检索”的方式,按照汉明距离式(7)计算V′与测试特征库图像的一级图像特征Vi的相似度sim(V′, Vi):
| $ sim\left({V', {V_i}} \right) = \sum\limits_{i = 1}^n {{s_k}} ;\;\;\;{s_k} = 1\left({{\rm{if}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_k}^\prime = {v_{ik}}} \right) $ | (7) |
通过预先设置的一级相似度阈值ξ,得到一级匹配结果,可获得二级待检测图像索引,根据索引分别从原始特征库和测试特征库提取索引图像的二级鲁棒特征进行相似性度量,根据度量结果作出是否存在拷贝关系的判断。参数ξ直接影响第二级特征匹配效率与准确性,设置太大则会导致大量漏检事件的发生,设置过小则会降低二级特征匹配效率。
对Corel数据库中的1000幅源图像及对应的拷贝图像作为测试集进行分析,当阈值ξ在0.75~0.90范围内变化时,二级待检测图像数量所占比例(不同阈值情况下,疑似拷贝图像数与1000幅图像的比值)如表 1所示,一级匹配之后阈值ξ对二级特征相似性度量耗时影响如表 2所示。
| 表 1 阈值对二级待检测图像数量影响 Table 1 Effect of threshold on number of secondary image to be detected |
由表 1~2可知,一级相似度阈值ξ设置为0.875时,其查全率及一级疑似拷贝图像进行二级匹配的匹配速度相对其他阈值情况下较高,故将一级匹配最佳阈值设置为0.875。
| 表 2 阈值对二级检索耗时影响 Table 2 Effect of threshold on secondary retrieval time |
从图像库任意选取5幅图像,以图像1为标准,其二级特征在不同的角度区间设置情况下20个拷贝版本与图像1的相似度如图 2所示。由图 2可知,在区间设置为10、20的情况下,虽然鲁棒性显著,但是独特性不够明显,拷贝检测时会影响正确率;在区间设置为30、40的情况下,独特性相比前两种区间设置方式显著提升,考虑到特征存储占用的内存空间、特征匹配速度等因素,方向区间设置最佳阈值可选为30。
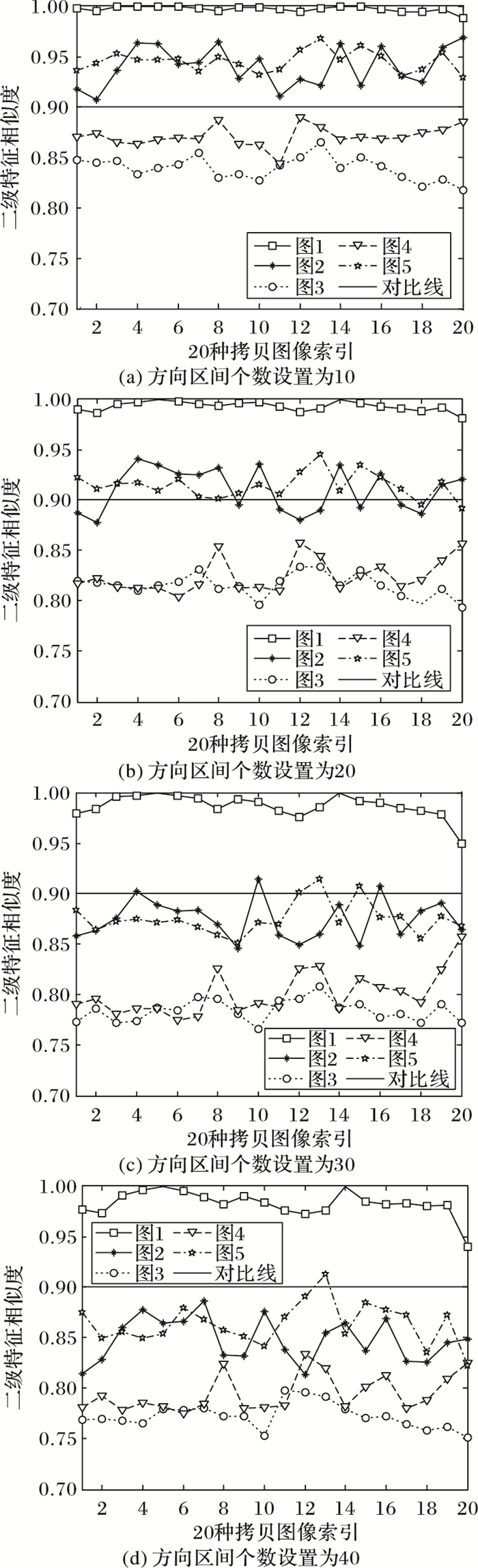
|
图 2 不同区间设置对比结果 Figure 2 Comparison results of different interval settings |
由表 1和图 2可知:单独生成一级特征或者二级特征作为图像的整体鲁棒特征,检测精度不理想;采用级联式检索框架,实验结果表明,本文算法在保证检测精度的同时亦大大提高了匹配速度。
2.4 图像拷贝检测评价标准为了评价所提算法,采用受试者工作特性曲线(Receiver Operating Characteristic Curve, ROC)表示其性能,定义真正类率(True Positive Rate, TPR)和假正类率(False Positive Rate, FPR)分别为:
| $ TPR = TP/(TP + FN) $ | (8) |
| $ FPR = FP/(FP + TN) $ | (9) |
其中:TP(True Positive)表示被模型预测为正的正样本,即哈希库中已注册数据被正确识别的数量;FN(False Negative)表示被模型预测为负的正样本,即哈希库中已注册数据未被识别出的数量;FP(False Positive)表示被模型预测为正的负样本,即哈希库中已注册数据未被正确识别的数量;TN(True Negative)表示被模型预测为负的负样本,即哈希库中未注册数据被正确识别的数量;ROC曲线横轴表示FPR,纵轴表示TPR,即正确识别率。设定阈值在一定范围内变化,可以得到一组TPR-FPR数据,绘制得到ROC曲线图,通过曲线与坐标轴围成的面积判断算法效果的优劣,面积越大算法性能越好。
3 仿真实验与分析 3.1 实验环境和数据本文的实验环境如下:Windows 7旗舰版操作系统,Intel Core i3-3120M 2.50 GHz CPU,4.00 GB内存,Matlab R2014a。
实验中,所选公共图像库为Corel图像库的1000幅图像(http://wang.ist.psu.edu/docs/related.html)。在此数据集上测试本文方法在各种图像变换下的匹配性能,图像库分别包含非洲人、海滩、建筑、公交车、恐龙、大象、花、马、山脉、食物等10种类别图像,该数据集中的测试图像包含模糊变换、几何变换和JPEG压缩等6种图像变换,失真类型、参数设置如表 3所示。根据本文提出的特征提取方法构建测试图像特征库。一级特征提取阶段角度区间p、距离区间q参数分别设置为8和5,二级特征提取阶段方向区间数量参数l设置30。二级特征匹配时阈值设置在0.80到0.95之间,在阈值区间均匀取10个值,每一个阈值得到一对TPR-FPR值,将所得数据绘制成ROC曲线。
| 表 3 构建测试库时失真操作类型及其参数设置 Table 3 Distortion operation types and their parameters setting when building test libraries |
对比SIFT算法生成128维描述子和本文算法生成4维描述子下平均特征生成时间, 如表 4所示。由于每幅图像特征点数量不一致,故提取时间也会存在差异,通过求取平均值可缩小计算误差。与传统方式生成128维信息相比,改进算法只生成4维信息,特征提取时间缩短为原来的1/20,可满足在线拷贝检测的需求。
| 表 4 不同算法对系统平均特征生成时间影响 Table 4 Effect of different algorithms on the the generation time of system average feature |
SIFT(128)、PCA-SIFT(36)、2DPCA-SIFT(n1=6, n2=3)、本文算法生成2000个特征描述以及4000000次特征匹配所需的时间,如表 5所示。
| 表 5 不同算法特征描述生成与匹配时间比较 Table 5 Time comparison of feature description generation and matching for different algorithms |
从表 5中可以看出,在特征提取阶段前三种方法特征生成时间基本上是一致的,本文算法相比于它们特征提取时间大大缩短,提取速度显著提高。在特征匹配阶段,可以看出虽然36维的匹配速度明显快于128维的SIFT特征匹配,但是本文算法采用的级联检索方式匹配速度上更快,一级匹配时间仅需0.53 s,在一级匹配结果上进行二级特征匹配则用时更短,仅用了0.21s,匹配时间缩短了1/2以上,明显优于对比算法。
另外,本文还分别验证在每一种攻击方式下本文算法检测精度,实验结果如图 3所示。图 3(a)是JPEG压缩情况下的ROC曲线,压缩因子高于50%时真正类率达到一个非常好的性能,低于50%时性能有所下降,原因是深度时量化步长增加,解压缩时图像像素变化较大,导致特征点增多,一定程度上降低了算法的鲁棒性与独特性,但总体上依然保持较好性能。图 3(b)对应的是伽玛校正情况下的曲线图,可以看出算法对伽玛校正的鲁棒性很好。图 3(c)对应的是添加噪声情况下的曲线图,相较于前几种失真操作,该操作性能有一定程度下降,原因是噪声对图像SIFT特征点提取影响较大,以至于相似性呈现一定差异。图 3(d)对应的是原始图像及裁剪和缩放情况下的曲线图,对于缩放操作,放大2倍时的性能明显优于放大1.5倍时,原因是放大能够较好保持原有数据,故放大程度越大,则效果越好。图 3(e)对应的是滤波情况下的曲线图,维纳滤波模板为5的曲线与坐标轴包围的面积最大,说明效果最好;均值滤波模板为3的曲线与坐标轴围成的面积略低于其他模板为3的滤波,均值滤波时通常采用邻域平均法,消弱了图像边缘,使图像变得有些模糊,影响了特征点的检测和匹配性能。图 3(f)对应的是旋转和剪切情况下的曲线图,从中可以看出,本文算法对图像的小范围角度的旋转鲁棒性很强;对于剪切操作,由于特征点的随机性使得特征可抵御一定程度的剪切变换,故拷贝检测效果也较好。
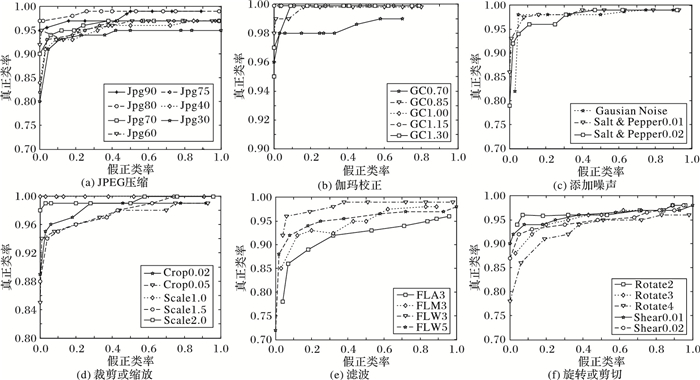
|
图 3 不同攻击方式下ROC曲线 Figure 3 ROC curve of different attack modes |
本文算法以SIFT特征点位置分布与方向分布特征为基础,为了能全面地测试特征描述方法的性能,故选取同样以SIFT特征为基础的图像拷贝检测算法作为对比,对比算法选择SIFT算法、PCA-SIFT算法,这些算法鲁棒性都很不错,都是经典算法,对比结果如图 4所示。由图 4可知,PCA-SIFT算法可以产生紧凑的低维数特,在特征描述维数、检索正确率以及低差错率下的匹配响应率等方面优于SIFT算法;但是,本文算法在生成特征维度较低的情况下,算法的鲁棒性和独特性仍然能保持较好的性能,明显优于对比的两种算法。

|
图 4 不同算法ROC对比结果 Figure 4 ROC comparison results of different algorithms |
为了在保证图像拷贝检测算法精度的同时提高特征提取速度与匹配效率,本文基于SIFT特征点分布特征提出了一种快速图像拷贝检测方法。该算法以SIFT特征点位置分布与方向分布特征构造两级式过滤框架,提高了特征提取速度与匹配速度,同时也保持了较好的鲁棒性与独特性。与现有基于SIFT的拷贝检测算法相比,该算法在保证检测精度的同时具有更好的时间性能。但是,当图像遭受JPEG压缩攻击,压缩因子进一步降低时,该算法鲁棒性不够理想,在保证检测精度的同时如何进一步降低特征描述的长度是以后的研究重点。
| [1] | 余艳伟, 周学海, 许华杰. 用于拷贝检测的鲁棒图像特征提取方法[J]. 武汉大学学报(理学版), 2013, 59(1): 87-92. (YU Y W, ZHOU X H, XU H J. A robust feature extraction scheme in image copy detection[J]. Journal of Wuhan University (Natural Science Edition), 2013, 59(1): 87-92.) |
| [2] | 刘炜, 欧阳建权, 李泽洲, 等. 运用边缘方向直方图进行图像拷贝检测[J]. 计算机工程与应用, 2010, 46(31): 184-187. (LIU W, OUYANG J Q, LI Z Z, et al. Edge histogram-based image copy detection algorithm[J]. Computer Engineering and Applications, 2010, 46(31): 184-187. DOI:10.3778/j.issn.1002-8331.2010.31.051) |
| [3] | 邹复好, 李晓威, 许治华, 等. 抗旋转和等比缩放失真的图像拷贝检测技术[J]. 计算机研究与发展, 2009, 46(8): 1349-1356. (ZOU F H, LI X W, XU Z H, et al. Image copy detection with rotation and scaling tolerance[J]. Journal of Computer Research and Development, 2009, 46(8): 1349-1356.) |
| [4] | KIM C. Content-based image copy detection[J]. Signal Processing:Image Communication, 2003, 18(3): 169-184. DOI:10.1016/S0923-5965(02)00130-3 |
| [5] | MONGA V, MIHCAK M K. Robust and secure image hashing via non-negative matrix factorization[J]. IEEE Transactions on Information Forensics and Security, 2007, 2(3): 376-390. DOI:10.1109/TIFS.2007.902670 |
| [6] | 王瑞, 郝娜, 张波, 等. 一种自适应Harris角点检测算法[J]. 火力与指挥控制, 2015, 40(7): 84-86. (WANG R, HAO N, ZHANG B, et al. Harris corners detection method based on self-adapting non-maximal suppression algorithm[J]. Fire Control & Command Control, 2015, 40(7): 84-86.) |
| [7] | 刘兆庆, 李琼, 刘景瑞, 等. 一种基于SIFT的图像哈希算法[J]. 仪器仪表学报, 2011, 32(9): 2024-2028. (LIU Z Q, LI Q, LIU J R, et al. SIFT based image hashing algorithm[J]. Chinese Journal of Scientific Instrument, 2011, 32(9): 2024-2028.) |
| [8] | 孙锐, 闫晓星, 高隽. 基于SIFT和PCA的图像感知哈希方法[J]. 电路与系统学报, 2013, 18(1): 274-278. (SUN R, YAN X X, GAO J. A perceptual image hashing method via SIFT and PCA[J]. Journal of Circuits and Systems, 2013, 18(1): 274-278.) |
| [9] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [10] | KE Y, SUKTHANKAR R. PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2004:506-513. |
| [11] | 颜雪军, 赵春霞, 袁夏. 2DPCA-SIFT:一种有效的局部特征描述方法[J]. 自动化学报, 2014, 40(4): 675-682. (YAN X J, ZHAO C X, YUAN X. 2DPCA-SIFT:an efficient local feature descriptor[J]. Acta Automatica Sinica, 2014, 40(4): 675-682.) |
| [12] | LYU X D, WANG Z J. Perceptual image hashing based on shape contexts and local feature points[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(3): 1081-1093. DOI:10.1109/TIFS.2012.2190594 |
| [13] | 许佳佳, 张叶, 张赫. 基于改进Harris-SIFT算子的快速图像配准算法[J]. 电子测量与仪器学报, 2015, 29(1): 48-54. (XU J J, ZHANG Y, ZHANG H. Fast image registration algorithm based on improved Harris-SIFT descriptor[J]. Journal of Electronic Measurement and Instrumentation, 2015, 29(1): 48-54.) |
| [14] | LING H F, YAN L Y, ZOU F H, et al. Fast image copy detection approach based on local fingerprint defined visual words[J]. Signal Processing, 2013, 93(8): 2328-2338. DOI:10.1016/j.sigpro.2012.08.011 |
| [15] | 张春美. 特征点提取及其在图像匹配中的应用研究[D]. 郑州: 信息工程大学, 2008: 10. (ZHANG C M. Study on feature point detecting and its application to image matching[D]. Zhengzhou:Information Engineering University, 2008:10.) http://cdmd.cnki.com.cn/Article/CDMD-90008-2009261519.htm |
| [16] | MIKOLAJCZYK K, SCHMID C. Performance evaluation of local descriptors[J]. IEEE Transaction on Pattern Analysis & Machine Intelligence, 2005, 27(10): 1615-1630. |




